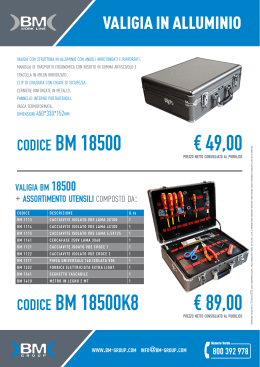
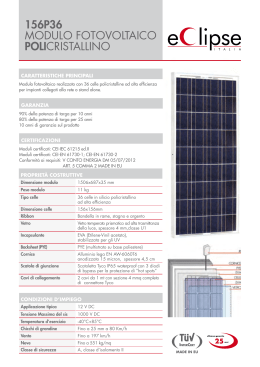
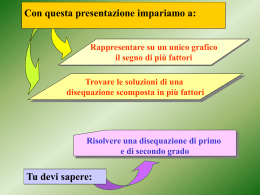
Alcune varianze (Var) e loro stime (v)
di stimatori che useremo oggi
1
2
3
θ̂
 θˆ  θ



Pr 
 k  1  α
 V(θˆ )

D  k V0
n
4
5
(stimatore della
proporzione)
6
 θˆ  θ



Pr 
 k  1  α
 V(θˆ )

n: stesse
formule
7
8
ESERCIZIO 1
9
SOL. ESERCIZIO 1
10
ESERCIZIO 2
11
SOL. ESERCIZIO 2
12
ESERCIZIO 3
13
SOL. ESERCIZIO 3
, quindi ad aumentare n.
14
ESERCIZIO 4
15
SOL. ESERCIZIO 4
16
SOL. ESERCIZIO 4
17
ESERCIZIO 5
Si vuole confrontare, a parità di errore campionario, la
numerosità di un canpione ST con quella di uno SSR.
I dati diinteresse sono riportati nella sreguente tabella:
strati
Nh
Sh2
Yh
1
800
120
10
2
500
110
20
3
100
80
30
Si vuole stimare il numero medio di giorni di vacanza di un individuo
appartenente alla popolazione di riferimento con un errore campionario
assoluto di 1,5 al livello 1-alfa=0,95. Definire:
1)La dimensione campionaria (con la formula esatta e con quella
approssimata) in un campionamento ST.
2)La dimensione campionaria (con la formula esatta e con quella
approssimata) in un campionamento SSR.
18
SOL. ESERCIZIO 5
1)
strati Nh
1
2
3
Yh
Wh
S h2
Sh2Wh
800
120
10 0,571429 68,57143
500
110
20 0,357143 39,28571
100
80
30 0,071429 5,714286
Sw2
1400
D
k
113,5714
1,5
1,96
170,32
0,5857
193,9093
19
SOL. ESERCIZIO 5
Sh2Wh
2)
N ed Nh grandi ,( Nh-1)/(N-1)=Nh/(N-1)=Wh
68,57143
39,28571
5,714286
113,5714
Wh ( yh  y ) 2
14,28571
8,928571
16,07143
39,28571
39,28571
S
2

W
h
S h2 
h
W
h
( yh  y)2
152,8571
h
15
Sw2
113,5714
220
20