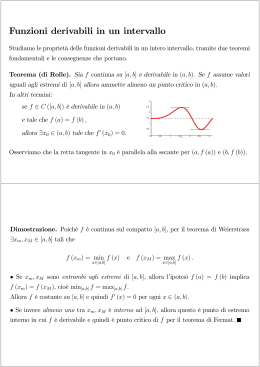
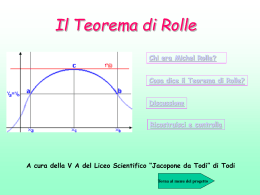
Funzioni continue su intervalli
Teoremi fondamentali del calcolo differenziale
Teorema
Se f(x) è una funzione continua in un intervallo I , allora f(I) è un intervallo.
f(I)
f(I)
I
y
x
I
x
 2
y
x 1
 2
x2
x2
Teorema di Weierstrass
Se f(x) è una funzione continua in un intervallo chiuso e limitato I , allora è
dotata in I di massimo e minimo.
M
I
m
I
y
1
x ( x  6) 2  1
8
y  tg (x )
Teorema di Weierstrass
Se f(x) è una funzione continua in un intervallo chiuso e limitato I , allora è
dotata in I di massimo e minimo.
3 per x  1

f ( x)   x per 1  x  5
2 per x  5

I
Teorema di Weierstrass
Se f(x) è una funzione continua in un intervallo chiuso e limitato I , allora è
dotata in I di massimo e minimo.
y  x 1
I  x  1
I
Teorema dei valori intermedi
Se f(x) è una funzione continua in un intervallo chiuso e limitato I , essa
assume almeno una volta qualunque valore compreso tra il suo minimo
assoluto e il suo massimo assoluto
M
k
k / m  k M
 xo / f(xo)=k
m
xo
x1
x2
Teorema dell’esistenza degli zeri
Se f(x) è una funzione continua in un intervallo chiuso e limitato I=[a,b] , e se
agli estremi dell’intervallo assume valori di segno opposto , essa si annulla in
almeno un punto interno dell’intervallo
f(b)
se f(a)*f(b)< 0
a
f(a)
c
 c / f(c)=0
b
a<c<b
f(c)=0
Esempio:
y  12 ( x  2)3  1
f(1)=-1,5 f(4)=3


f 23 2  0
Teorema di Rolle
Sia f(x) una funzione continua in [a,b] e derivabile in ]a,b[ e tale che f(a)=f(b)
allora esiste almeno un punto c  [a,b] tale che f(c)=0.
Per il teorema di Weierstrass f(x) ha un massimi M e un minimo m
1° caso m=M
 f(x) è costante  f(x)=0
x[a,b] f(x)=0
m=M
a
b
2° caso m<M
f(c)=0
f(c)=M
sia c il punto interno ad [a,b] tale che f(c)=M
scegliamo h tale che c+h [a,b].
f(c+h)-f(c)0
f(c+h)
f(a)=f(b)
dividiamo per h
se h>0
se h<0
f (c  h)  f (c )
0
h
f (c  h)  f (c )
0
h
se facciamo tendere h a zero:
f ' c   0
a
c
c+h
b
f ' c   0
poiché f(x) è derivabile in ]ab[
f(c)=0
Esempio
21x  x 3
y
10
in [1,4] si ha f(1)=f(4)=2
f'
 7 0
Sia f(x) una funzione continua in [a,b] e derivabile in ]a,b[ e tale che f(a)=f(b)
allora esiste almeno un punto c  [a,b] tale che f(c)=0.
x  [a,b] f(x)0.
Esempio:
se 1  x  3
2 x
y
 2 x  12 se 3  x  5
f(a)=f(b)
non è derivabile in x=3
a
c
b
Teorema di Lagrange o del valor medio
Sia f(x) una funzione continua in [a,b] e derivabile in ]a,b[ allora esiste almeno un punto
f (b )  f (a )
c  [a,b] tale che :
 f ' (c )
ba
f(b)
Si considera
g( x)  f ( x) 
g ' ( x)  f ' ( x) 
f (b )  f (a )
ba
f (b )  f (a )
x
ba
g(a)=g(b)
per il teorema di Rolle
c  [a,b] tale che g(c)=0
g ' (c )  f ' (c ) 
f (b )  f (a )
0
ba
f(a)
a
c
b
f (b )  f (a )
 f ' (c )
ba