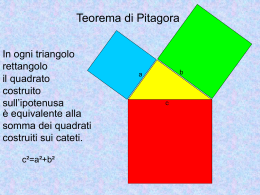
Copyright Luisa Camnasio
uso consentito solo per le attività didattiche dell’Iti «Fermi» di Desio
Siamo nel V secolo avanti
Cristo, in una località della
Magna Grecia,
probabilmente sulle coste
dell'Italia meridionale, nei
pressi di Crotone.
Primo atto:
tutto è numero!
Quali erano i numeri incaricati
di esprimere il mondo e
l'armonia, i numeri che
avevano il compito di
descrivere il cosmo?
I NUMERI INTERI
Quali erano i numeri incaricati
di esprimere il mondo e
l'armonia, i numeri che
avevano il compito di
esprimere il cosmo?
E ANCHE LE
FRAZIONI
Quali erano i numeri incaricati
di esprimere il mondo e
l'armonia, i numeri che
avevano il compito di
esprimere il cosmo?
MA SOLO NUMERI
POSITIVI!
Questi numeri, definiti in
seguito razionali,
permettevano di…
esprimere numericamente
grandezze geometriche e, quindi,
misurarle.
Secondo atto:
l’arrivo della
diagonale del
quadrato di lato 1
LATO
CHE RAPPORTO ESISTE TRA
LATO E DIAGONALE?
Prendiamo il quadrato più semplice,
quello con il lato uguale a 1
1
Qual è la lunghezza della sua
diagonale?
1
La diagonale divide il quadrato in due
triangoli rettangoli isosceli
1
La diagonale divide il quadrato in due
triangoli rettangoli isosceli
1
TRIANGOLI RETTANGOLI…?
Teorema
di…
PITAGORA!!!
In ogni triangolo
rettangolo il
quadrato costruito
sull’ipotenusa è
equivalente alla
somma dei quadrati
costruiti sui cateti
QUINDI:
quadrato della
diagonale
1
=
1
2
1
+
2
1
QUINDI:
quadrato della
diagonale
1
=
1
1 + 1
QUINDI:
quadrato della
diagonale
1
=
1
2
Ecco l’informazione
essenziale:
la lunghezza della
diagonale è un numero
il cui quadrato è 2
Che
numero
è?
Questo
numero
esiste
davvero?
E se non
esiste…
come
accertarsene?
Terzo atto:
la crisi della
visione
pitagorica
legame tra
numeri e
grandezze
Il lato e la diagonale di un quadrato
sono incommensurabili
CRISI DELL’UNIVERSO DEI PITAGORICI
FINO A QUEL
MOMENTO:
tutto ciò che
si può
costruire si
può
“misurare”
RIVELAZIONE:
La misura di
alcune
grandezze non si
può esprimere
con un numero
razionale
La prima
dimostrazione
nella storia della
matematica è stata
una dimostrazione
di impossibilità
È venuto il
momento di
affrontare questa
famosa
dimostrazione…
ENUNCIATO:
Non esiste alcun
numero razionale il
cui quadrato sia
uguale a 2
DIMOSTRAZIONE:
Procediamo per assurdo
supponendo che
esista almeno un numero
razionale n tale che
2
n
=2
DIMOSTRAZIONE:
Per definizione, n si può
scrivere come rapporto
di due numeri interi a, b:
a
n=
b
DIMOSTRAZIONE:
Possiamo supporre che:
MCD(a,b) = 1
a
n=
b
2
n
=
2
a
2
b
DIMOSTRAZIONE:
2
n
=
2
a
2
n
2
b
2
a
2
b
=2
=2
DIMOSTRAZIONE:
2
a
2
b
2
a =
=2
2
2
b
DIMOSTRAZIONE:
2
a =
2
2
b
2
a
a è pari
è pari
a = 2c
2
a =
2
4c
2
2c =
2
b
=
2
2b
DIMOSTRAZIONE:
2
b è
Quindi
pari e, di
conseguenza, anche b lo è
???
Ma questo è impossibile!!!
Infatti a è pari e MCD(a,b) = 1
CONCLUSIONE:
È ASSURDO SUPPORRE
CHE ESISTA UN NUMERO
RAZIONALE IL CUI
QUADRATO È 2
cvd
COME SI AMPLIA L’INSIEME
DEI NUMERI RAZIONALI?
Consideriamo il problema del
numero il cui quadrato è 2.
Tale numero non esiste in Q, come
abbiamo dimostrato
COME SI AMPLIA L’INSIEME
DEI NUMERI RAZIONALI?
Possiamo però cercare di “avvicinarci” il
più possibile alla soluzione, usando dei
numeri razionali.
Costruiamo cioè due “successioni” di
numeri razionali i cui quadrati si
avvicinano, rispettivamente per eccesso
e per difetto, a 2
COME SI AMPLIA L’INSIEME
DEI NUMERI RAZIONALI?
1
1,4
1,41
1,414 1,4142
2
1,5
1,42
1,415 1,4143
Il quadrato dei numeri in rosso è minore di 2,
quello dei numeri in blu è maggiore di 2. Inoltre i
numeri in rosso differiscono da quelli in blu di
un’unità di ordine via via inferiore: 1, 1/10,
1/100, 1/1000...
COME SI AMPLIA L’INSIEME
DEI NUMERI RAZIONALI?
1
1,4
1,41
1,414 1,4142
2
1,5
1,42
1,415 1,4143
Non troveremo mai un numero razionale il cui
quadrato è 2, ma possiamo restringere quanto
vogliamo l’intervallo intorno alla “lacuna” che c’è,
nell’insieme dei numeri razionali rappresentati su
una retta orientata, in corrispondenza del
segmento che è la diagonale del quadrato di lato 1
COME SI AMPLIA L’INSIEME
DEI NUMERI RAZIONALI?
0
1
2
COME SI AMPLIA L’INSIEME
DEI NUMERI RAZIONALI?
0
1
LACUNA
2
COME SI AMPLIA L’INSIEME
DEI NUMERI RAZIONALI?
1
1,4 1,5
2
COME SI AMPLIA L’INSIEME
DEI NUMERI RAZIONALI?
1,4
1,5
1,41 1,42
E COSÌ VIA
COME SI AMPLIA L’INSIEME
DEI NUMERI RAZIONALI?
Una coppia di successioni come quelle con
cui abbiamo “assediato” la diagonale del
quadrato di lato 1 definisce un numero reale.
Non è facile lavorare con la definizione
rigorosa dei numeri reali, elaborata da
Dedekind, che definisce i numeri reali come
coppie di particolari insiemi di numeri
razionali, detti “sezioni”.
COME SI AMPLIA L’INSIEME
DEI NUMERI RAZIONALI?
Definiremo quindi un numero reale
come allineamento decimale.
In particolare un allineamento
decimale non periodico, non potendo
essere trasformato in una frazione, si
dice NUMERO IRRAZIONALE.
COME SI AMPLIA L’INSIEME
DEI NUMERI RAZIONALI?
NUMERI RAZIONALI
allineamenti decimali
periodici
NUMERI IRRAZIONALI
allineamenti decimali
NON periodici
NUMERI
REALI
COME SI AMPLIA L’INSIEME
DEI NUMERI RAZIONALI?
Per operare più agevolmente
con i numeri reali senza
ricorrere ad approssimazioni,
definiremo i “radicali” e ne
studieremo le proprietà.