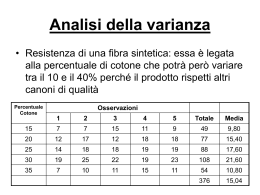
Stimatore della varianza


2 1  f1 2
ˆ
v YSMGR  N '
sr
m
CAMPIONAMENTO A DUE STADI
i 
N
YˆDS 
n
 
n mi
N Mi
 n mi mi  1
 N M M  1 i  i'
i
i
 (i , j )i ',k   
n mi n  1 mi '

i  i'
M
i
'
 N M i N  1
 Yˆ
ic
i


2
1
N
2 1  f1
ˆ
ˆ
ˆ
1
v YDS  N
Y

Y

 i n i n
n n 1
 M i2
1  f 2i 2
S 2i
mi
Quando N/n>>1 posso usare solo la prima parte di varianza, il rischio di commettere un errore è molto
maggiore al primo stadio, estraggo pochi grappoli rispetto al totale, quindi rischio di fare un grande
errore al primo stadio.
ESERCIZIO 1
SOLUZIONE ES. 1
SOLUZIONE ES. 1


2 1  f1 2
ˆ
v YSMGR  N '
sr
m
= 4410
GRAPPOLI OMOGENEI
ESERCIZIO 2
Il proprietario di una palestra milanese, vuole stimare il numero
totale di volte in cui i 100 clienti, iscrittisi nel dicembre 2006 , si
sono recati in palestra nel mese successivo. A tal fine seleziona
un campione sistematico di 10 degli iscritti, chiede loro il numero
di allenamenti effettuati nel gennaio 2007, ottenendo le seguenti
risposte:
16
18
22
12
9
14
21
8
25
10
a)Dopo aver definito il passo di campionamento, stimare il totale
degli ingressi di gennaio dei 100 iscritti oggetto di interesse.
 
b)fornire la stima della varianza dello stimatore, v Yˆsm .
  
c)dire sotto quali condizioni vale la relazione : v Yˆsm  v Yˆ
SOLUZIONE ESERCIZIO 2
a)
16
N =100
n =10
k=N/n=10
18
22
= 1550
= 31250
12
9
14
21
8
25
10
SOLUZIONE ESERCIZIO 2
c)
ESERCIZIO 3
SOLUZIONE ESERCIZIO 3
a)definire per il piano di campionamento le frazioni di sondaggio del primo
e del secondo stadio e le probabilità di inclusione del primo e del secondo
ordine .
 n mi mi  1
 N M M  1 i  i'
i
i
 (i , j )i ',k   
n mi n  1 mi '

i  i'
M
i
'
 N M i N  1
SOLUZIONE ESERCIZIO 3
c)Quando N/n>>1 posso usare solo la prima parte di varianza, il rischio di
commettere un errore è molto maggiore al primo stadio, estraggo pochi
grappoli rispetto al totale, quindi rischio di fare un grande errore al primo
stadio.
ESERCIZIO4
L’amministrazione comunale di una città, prima di iniziare i lavori
necessari per il cablaggio, desidera conoscere quante famiglie residenti
sul territorio sarebbero interessate ad un collegamento telefonico e di
video-on-demand che utilizzi le fibre ottiche. L’amministrazione
decide di selezionare casualmente 3 dei 10 quartieri comunali ed
intervistarne l'8% delle famiglie residenti. I risultati forniti dalla
rilevazione sono sintetizzati nella seguente tabella:
quartieri
1
n.° famiglie residenti
350
n.° famiglie interessate alle 12
fibre ottiche
s2i
18
2
3
528 876
38 60
12
15
a) Descrivere il piano di campionamento scelto dall'amministrazione
comunale e stimare il numero totale di famiglie interessate al
collegamento con fibre ottiche.
b) Si descriva inoltre il significato delle singole componenti che
definiscono la varianza dello stimatore impiegato al punto a).
c) Nel caso i risultati campionari fossero stati ottenuti intervistando
tutte le famiglie residenti nei quartieri estratti in primo stadio,
quale stimatore sarebbe stato opportuno per stimare il totale di
famiglie interessate al collegamento con fibre ottiche?
SOLUZIONE ESERCIZIO 4
a) Nel caso considerato è stato utilizzato un campionamento a due stadi con frazione di
sondaggio di primo stadio f1  0,3 e frazione di secondo stadio costante f 2  0,08 (m 1=28,
m 2=42, m 3=70). A partire da Yˆ  150 , Yˆ  477,7143 , Yˆ  750,8571 , lo stimatore Yˆ
1
2
3
DS
risulta pari a 4595,238.
b) La varianza totale risulta v YˆDS  3101838,463 , con varianza di primo stadio pari a
2111794,921 e varianza di secondo stadio pari a 990043,5429. Per la descrizione delle
singole componenti, vedi libro (par. 4.6).
c) In questo caso lo stimatore da utilizzare è YˆGR .
 
ESERCIZIO 5
Un Tour Operator vuole riorganizzare i centri diving dislocati nei vari villaggi
turistici di sua proprietà, effettua quindi una indagine per conoscere in che
misura i vari centri vengono sfruttati dai turisti alloggiati nei villaggi. A tale
scopo si decide di scegliere casualmente 5 dei 50 villaggi che dispongono di un
diving center situati nel Mar Rosso, Maldive, Messico e Mediterraneo e di
intervistare il 50% degli ospiti. Tra le variabili rilevate si consideri la Y= n.°
immersioni subacque fatte in un a settimana di soggiorno presso il villaggio, il cui
valore viene riportato nella terza riga della seguente tabella:
Villaggio estratto 1
n° tot. Ospiti
650
n° immersioni
932
2
420
525
3
110
324
4
400
680
5
250
558
a) Si stimi il numero di immersioni che mediamente un ospite del villaggio
effettua in una settimana, sapendo che il numero totale degli ospiti del Tour
Operator ogni settimana è 18000;
b) Si stimi, in forma approssimata, la varianza dello stimatore;
SOLUZIONE ESERCIZIO 5
a) Si tratta di un piano di campionamento a due stadi, in cui bisogna stimare il
valor medio delle unità elementari. Si può impiegare lo stimatore (6.50)
oppure lo stimatore (6.48) diviso per 18000. YˆDS  3.354444
b) Nel campionamento a due stadi una forma approssimata della stima della
varianza è data dalla varianza di primo stadio: formule (6.53) oppure (4.51)
primo addendo diviso per 18000^2. V YˆDS  0.27794
 
ESERCIZIO 6
SOLUZIONE ESERCIZIO 6
ESERCIZIO 7
SOLUZIONE ESERCIZIO 7
Seguendo il metodo alternativo:
ESERCIZIO 8
Per introdurre una indennità informatica oraria nelle sedi regionali di
una amministrazione dello Stato si è interessati a valutare il totale
delle ore trascorse giornalmente dagli impiegati davanti ai
videoterminali. Si suppone che il piano di campionamento preveda una
prima estrazione con probabilità costanti di 4 delle 20 sedi regionali ed
una successiva estrazione, sempre con probabilità costanti, pari al 25%
degli impiegati in ciascuna sede. Dopo aver riscontrato i seguenti
risultaticampionari:
a) si definiscano per il piano di campionamento in esame le probabilità
di inclusione di primo e del secondo ordine;
b) si stimi il numero totale delle ore trascorse davanti ai videoterminali
dagli impiegati delle 20 sedi e si calcoli la varianza dello stimatore
utilizzato;
c) si valutino le condizioni per cui è sufficiente stimare la varianza in
forma approssimata.
SOLUZIONE ESERCIZIO 8
Come si può notare il contributo del secondo termine è alquanto
modesto, rispetto a quello del primo; in genere,quando il coefficiente
di espansione N/n >>1, una stima approssimata per difetto della
varianza dello stimatore viene fornita dalla varianza di primo stadio.
ESERCIZIO 9
Per stimare il numero di errori di digitazione compiuti da un operatore
incaricato di inserire le risposte fornite in 80 questionari, viene
estratto un campione sistematico di 8 questionari.
I. Definire il passo di campionamento ed i possibili campioni estraibili.
II. Supposto che i questionari estratti confrontati con la matrice dati
abbiano fornito il numero di errori di digitazione pari a 1, 3, 2, 4, 0, 0,
12, si stimi il totale degli errori di digitazione e la varianza dello
stimatore.
III. Si spieghino le modifiche da apportare allo stimatore ed alla
relativa varianza nel caso si scelgano m campioni di ampiezza n/m
invece di un singolo campione di numerosità n.
SOLUZIONE ESERCIZIO 9
SOLUZIONE ESERCIZIO 9
Vengono estratti m numeri casuali r1,….rm nell’intervallo [1,mk], ciascuno
dei quali fornisce un campione formato dalle unità [ri+(j-1)mk]. In questo
modo la popolazione risulta divisa in mk grappoli di uguale dimensione e si
sceglie un campione di m grappoli; pertanto sia le probabilità di inclusione
che la varianza dello stimatore si ricavano dalle formule del campionamento
a grappoli