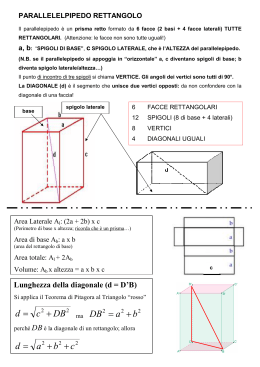
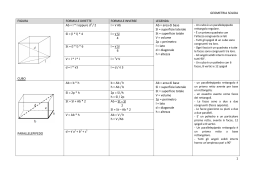
I POLIEDRI
I POLIEDRI
sono solidi delimitati da poligoni
UN PRISMA è UN POLIEDRO
con due facce PARALLELE: LE BASI
BASI
FACCE
LATERALI
e tante FACCE LATERALI quanti sono
i lati del poligono di base
Prende il nome dalla base

a base esagonale

a base pentagonale

a base triangolare

parallelepipedo
rettangolo
IL CUBO
 LE SUE FACCE SONO QUADRATI
 LE TRE DIMENSIONI SONO UGUALI:
l
l
l
l
Osserva lo sviluppo di un cubo
2 cm
2 cm
2 cm
2 cm
La superficie laterale è composta
da 4 quadrati equivalenti
Ab  l  Al  l  4
2
2
2 cm
2 cm
Esempio
Al  2  4  4  4  16 cm
2
2
La superficie totale è composta
da 6 quadrati equivalenti
Ab  l  At  l  6
2
2
2 cm
2 cm
Esempio
At  2  6  4  6  24 cm
2
2
Per calcolare il volume
si eleva la misura dello spigolo alla
terza.
3
V l
Esempio
Il primo strato è formato
da 3 x 3 = 9 unità
Ci sono 3 strati da 9 unità
quindi:
3 x 3 x 3 = 33 = 27 unità
V  3  27 cm
3
3 cm
3 cm
3 cm
3
IL PARALLELEPIPEDO
RETTANGOLO
IL PARALLELEPIPEDO
RETTANGOLO
 LE SUE FACCE SONO RETTANGOLI
 HA TRE DIMENSIONI:
l’altezza (c)
e le due dimensioni di base (a e b)
c
b
a
Osserva lo sviluppo di un
parallelepipedo
Le facce laterali formano un
rettangolo
Per calcolare l’area della
superficie laterale: Al  2 pb  h
h
2pb
Esempio
Al  (5  2)  2 6  14  6  84 cm
2
Per calcolare l’area della
superficie totale: At  Al  Ab  2
Ab
Al
Ab
Esempio
Ab  5  2  10 cm
2
At  84  10  2  84  20  104 cm
2
Per calcolare il volume
Ab
7 cm
4 cm
Si moltiplica l’area di base per
l’altezza: Ab  a  b 
3 cm
V  Ab  h oppure V  a  b  h
Esempio
V  3  4  7  84 cm
3
I PRISMI
LA SUPERFICIE LATERALE
h
2pb
Al  2 pb  h
LA SUPERFICIE TOTALE
h
Ab
At  Al  Ab  2
Il volume
Ab
Ab
h
h
Si moltiplica l’area di base per
l’altezza:
V  Ab  h
RIEPILOGO

PRISMI
Al  2 pb  h
At  Al  2  Ab
V  Ab  h

PARALLELEPIPEDO
Al  2 pb  h
At  Al  2  Ab
V  Ab  h

CUBO
Al  l  4
2
At  l 2  6
V l
3