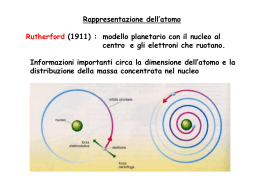
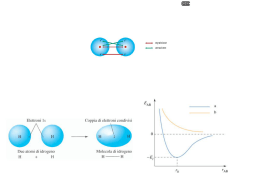
Radiazione del corpo nero λpeak=5,27 x 10-7nm λpeakT=b λpeak=5,8 x 10-7nm λpeak=6,4 x 10-7nm λpeak=7,2 x 10-7nm λpeak=8,3 x 10-7nm Contrasto con la teoria di Maxwell Catastrofe dell’ultravioletto Oscillatori armonici Scoperta di di Planck E/f =nh L’energia contenuta in un segnale monocromatico, rapportata alla sua frequenza specifica permetteva di ottenere un valore sempre multiplo intero di h=6,6 x10-34 Jxs E=hf pacchetto minimo di energia quantum Soluzione del problema del corpo nero Dato che ogni colore può essere emesso solo con un numero intero di pacchetti specifici (nhf) l’energia totale contenuta in un corpo nero, assegnata casualmente a tutti i colori, vedrà una distribuzione di tipo statistico, gaussiano. Einstein e l’effetto fotoelettrico Studiando l’effetto fotoelettrico, Einstein dimostra che un onda luminosa è costituita da «pacchetti di energia» pari a E=hf cui è associata una quantità di moto q=h/λ (h=costante di Planck) . A tali «pacchetti» fu assegnato il nome di fotoni. La scoperta di Einstein mise in «luce» ha natura dualistica dell’elettromagnetismo: 1.La luce ha proprietà ondulatorie (descritte dalla teoria di Maxwell) 2.La luce ha proprietà particellari (descritte dalla teoria di Planck-Einstein) Analisi spettrale Emissione continuo Corpo nero Gas rarefatto incandescente Gas rarefatto freddo Corpo nero Emissione a righe Assorbimento Emissione / Assorbimento da parte di un gas rarefatto Accumulo delle righe Spettro dell’idrogeno Serie di Paschen n1=3 Serie di Balmer n1=2 Serie di Lyman n1=1 Le righe non sono disposte a caso! Equazione di Rydberg Permette di ottenere tutte le lunghezze d’onda delle righe dell’idrogeno Le righe non sono disposte a caso, ma ubbidiscono ad una legge matematica! R =costante di Rydberg) n1= numero d’ordine di zona spettrale n2= numero d’ordine di riga Partendo dalle equazioni di Maxwell non si riusciva a spiegare l’equazione di di Rydberg! Anche in questo caso la teoria classica dell’elettromagnetismo non funzionava! Occorreva ancora una volta una intuizione come quella di Planck. Le ben definite righe spettrali suggerirono a Bohr l’idea della «quantizzazione»… ma di cosa? Bohr, come Planck, pazientemente lavorò con formule e calcoli fino a giungere ad una conclusione: Ponendo il momento angolare dell’elettrone che ruota attorno al nucleo Riprendendo le formule di Rutherford per l’energia dell’elettrone, combinandole l’equazione di Planck e con la formula imposta mvr= nh/2π , riuscì a «giustificare» l’equazione di Rydberg. Questo significò ammettere che le orbite dell’elettrone sono «quantizzate». Sono permesse solo quelle che hanno un momento angolare multiplo intero n del valore h/2π Dato che ad ogni orbita è associato un valore di energia, anche le energie saranno quantizzate mvr= nh/2π n=numero intero La teoria di Bohr si può riassumere nei seguenti postulati: 1. L’elettrone in un atomo si muove secondo un’orbita circolare intorno al nucleo ed il suo moto è regolato dalla forza elettrica di Coulomb tra l’elettrone carico negativamente e il nucleo carico positivamente e dalla forza centrifuga. 2. Il moto dell’elettrone è descritto dalle leggi di Newton, ma non tutte le orbite sono permesse: solo quelle di raggio r tale che il momento angolare mvr dell’elettrone sia multiplo intero di h/2π essendo h la costante di Planck ovvero: mvr = nh/2π 3. Se l’elettrone permane in un’orbita, non emette una radiazione elettromagnetica e pertanto la sua energia è costante: l’orbita viene detta orbita stazionaria. 4. Una radiazione elettromagnetica viene assorbita o emessa solo quando un elettrone salta da un’orbita all’altra: L’energia assorbita o emessa è «quantizzata», vale un quantum ΔE = hν . Il salto di orbita è definito «salto quantico». In pratica Bohr giunse alla formula empirica di Rydberg partendo da leggi di Newton-Maxwell ma imponendo una condizione: i valori del momento angolare mvr sono multipli interi n di una quantità minima h/2π. Questo, ovviamente, comporta l’esistenza di specifiche e determinate orbite permesse all’elettrone quantizzazione delle orbite. L’elettrone passando da un’orbita all’altra assorbe o emette solo determinate quantità di energia, multipli interi del quantum di Planck ΔE=nhf (differenza di energia tra le due orbite) e quindi ben precise righe spettrali. Lo stesso elettrone potrà fare salti differenti (ad es dall’orbita 1 alla 2 o direttamente alla 5, per poi scendere alla 4, risalire alla 6, ridiscendere alla 1 ecc). Per questo il singolo elettrone dell’idrogeno assorbe ed emette numerose righe spettrali (ma sempre le stesse). Bohr chiama le orbite Livelli energetici cui assegna un numero quantico intero n=1,2,3,4,5,6,7 Per chi vuole approfondire, ecco come Bohr dimostra la sua teoria! 1. 2. 3. 4. 5. 6. 7. 8. 9. All’elettrone, in quanto oggetto che ruota, è associato un momento angolare L=mvr Data la stabilità dell’atomo, il momento angolare si conserva nel tempo mvr=cost. Da cui r=cost/mv Il raggio atomico dell’idrogeno H, da varie sperimentazioni, è risultato 0,5 angstrom Conoscendo la massa m dell’elettrone (da Thomson-Millikan) e la sua velocità v (da Rutherford) è possibile ricavare il valore della costante cost Tale valore risultò pari alla costante h di Planck divisa per 2π cost=h/2π. Quindi, per l’H allo stato fondamentale, posso scrivere mvr0=h/2π Se eccitato, l’elettrone certamente cambia orbita (si allontana dal nucleo) per acquistare un nuovo momento angolare mvr1 con un altro valore della costante. Posso ora ipotizzare che il nuovo valore non sia qualsiasi, ma multiplo intero di quello iniziale mvr1= nh/2π (dove n= 1,2,3,4… numero intero). Da questa formula ricavo la velocità v=nh/2πmr1 Da Rutherford sappiamo che in una determinata orbita, per l’equilibrio tra forza centrifuga Fc e forza elettrostatica di Coulomb Fel, mv2/r=Kelq2/r2. In questa formula sostituisco la velocità v2 come nel punto 7. ottengo mn2h2/4π2m2r13=Kelq2/r12 Semplifico e trovo il raggio r1=n2h2/Kelq24π2m 10. Sappiamo anche da Rutherford che ad una determinata orbita corrisponde una specifica energia totale dell’elettrone E= -1/2 x Kelq2/r 11. Tra due orbite esisterà una differenza di energia dE= E2 – E1 = -1/2 x Kelq2/r2 + 1/2 x Kelq2/r1 12. Sostituisco i due raggi con la formula del punto 9. dE= 2Kel2 q4 m π2/n12h2 (1/n22 – 1/n22) 13. Ma dE è una radiazione elettromagnetica quindi dE=hf dove f=C/ λ. Sostituisco 1/ λ = R(1/n1 – 1/n2) 14. Si arriva, cioè, alla formula empirica delle righe spettrali Dalle orbite circolari alle orbite ellittiche Le righe impreviste H Il modello atomico di Bohr spiega bene il comportamento spettroscopico dell'idrogeno e, in parte, quello di alcuni metalli alcalini come il litio ed il sodio, ma si rileva del tutto inadeguato per l'interpretazione degli spettri di altri elementi. Lo spettro dell'elio, per esempio, non si accorda con le previsioni del modello di Bohr in quanto, accanto a righe previste, vi si trovano delle righe non previste (non ottenibili, cioè, da formule analoghe a quella di Rydberg). He ? Righe non previste Il numero quantico secondario l Sommerfeld cercò di «aggiustare» il modello di Bohr proponendo l’idea che le orbite potessero avere forma non solo circolare ma anche ellittica con differente eccentricità. Così il numero del livello energetico di Bohr fu indicato come numero quantico principale n (con valore da 1 a 7). Ad ogni forma dell’orbitale, invece, fu assegnato un valore intero indicante l’eccentricità (0 compreso), gli fu assegnata la lettera l e fu definita numero quantico secondario (o semplicemente sottolivello energetico). Orbite possibili nel terzo livello Dall’analisi spettrale Sommerfeld ricavò i seguenti sottolivelli l, nei rispettivi livelli n: 1) 2) 3) 4) l=0 l=0, l=1 l=0, l=1, l=2 l=0, l=1, l=2, l=3 Per i livelli superiori non riscontrò orbite con l>3 Come si può notare: più alto è il livello energetico n (più lontano dal nucleo), più sono i sottolivelli possibili (le forme delle orbite). Questo risulta facilmente comprensibile: l’elettrone ha più spazio a disposizione, si può muovere con maggiore libertà! Il 3° numero quantico: l’orientamento magnetico m Altra «stranezza» degli spettri atomici (già conosciuta nel 1800 come effetto Zeeman) è quella che, in vicinanza di campi magnetici, molte righe spettrali si moltiplicano. Per spiegare quest’effetto si propose un terzo numero quantico definito numero quantico magnetico m. Tale numero indicherebbe l’orientamento possibile nello spazio di una determinata orbita ellittica (un’orbita circolare non ha orientamento). A causa dell’orbita ellittica, infatti, l’elettrone genera un leggero campo magnetico con un orientamento dipendente dall’orientamento nello spazio dell’asse maggiore dell’orbita stessa. In assenza di campi magnetici esterni questo fenomeno non si nota. Tuttavia, avvicinando per esempio una calamita, il suo campo magnetico interagisce con quello generato dall’elettrone provocando una modifica dell’orbita che assumerà momentaneamente un altro valore di energia (spostamento delle righe spettrali). La comparsa di più righe spettrali (al posto di una originale) è segno della compresenza di più orbite aventi la medesima forma ellittica (quindi stessa energia iniziale stessa riga spettrale) ma orientamento nello spazio differente: questo farà sì che l’interazione con il campo magnetico esterno sia differente e porti a modifiche di orbita e di energia parimenti differenti (moltiplicazione delle righe) Sommerfeld calcolò che più «schiacciata» è l’ellisse, più orientamenti essa poteva assumere. Per l’orbita circolare fu trovato numero quantico magnetico m=0 (ed è unico); per l’orbita l=1 tre numeri quantici m=(-1 , 0, +1); all’orbita l=2 cinque numeri quantici m=(-2 , -1, 0, +1, +2), per l’orbita con l=3, sette numeri quantici m=(-3 , -2 , -1, 0, +1, +2 , +3). Effetto Zeeman Il 4° numero quantico lo spin s Altri «effetti magnetici» portarono a ipotizzare un ulteriore numero quantico, quello di spin s indicante il verso di rotazione dell’elettrone attorno al proprio asse (orario o antiorario). A tale numero s furono dati due valori s= +1/2 h ed s=-1/2 h dove h=costante di Planck Nel 1925 l’italiano Pauli dimostrò che nella stessa orbita possono muoversi due elettroni purchè abbiano gli spin antiparalleli. Un terzo elettrone ne sarebbe escluso principio di esclusione di Pauli. La spiegazione è da ricercare nelle interazioni elettromagnetiche degli elettroni… Essendo di carica uguale due elettroni si respingerebbero per la forza elettrostatica di Coulomb, ma ruotando in senso inverso (spin antiparalleli) generano intorno campi magnetici aventi orientamento Nord-Sud che tendono a far attrarre gli elettroni stessi. Forza elettrica e forza magnetica, così, trovano un equilibrio mantenendo gli elettroni sulla stessa orbita, ma a debita distanza l’uno dall’altro. Un terzo elettrone, oltre ad avere carica elettrica uguale agli altri due, si trova ad avere uno spin parallelo ad uno di essi. La situazione vedrebbe la repulsione da parte di due campi elettrici e di uno magnetico e l’attrazione solo da parte di un campo magnetico la sommatoria delle interazioni risulterà una forza repulsiva (esclusione dall’orbita). Riassumendo Atomo di Sommerfeld-Bohr L’elettrone percorre orbite stazionarie con momento angolare mvr=nh/2π che si possono trovare su uno dei 7 livelli energetici dell’elettrone numero quantico principale n (valori : 1,2,3,4,5,6,7) All’interno di ogni livello l’orbita può essere circolare oppure ellittica con specifica eccentricità Sottolivello energetico o numero quantico secondario l (valori da l=0 a l=n-1) Per le orbite ellittiche esistono diversi orientamenti nello spazio numero quantico magnetico m (valori da m= - l a m= + l, compreso m=0) In ogni orbita l’elettrone può avere rotazione attorno al proprio asse in senso orario o antiorario numero quantico magnetico di spin s (valori +1/2 h e -1/2 h). Dalle orbite alle… onde! De Broglie: un’altra idea rivoluzionaria Le continue modifiche e integrazioni miglioravano sempre di più il modello atomico di Bohr, ma non riuscivano a raggiungere la perfezione (corrispondenza perfetta tra equazioni e righe spettrali dei vari elementi). Si cercavano perciò nuove teorie, nuove spiegazioni, nuovi modelli per l’atomo quantistico. Fortunata, a tal proposito, fu l’intuizione di De Broglie il quale propose di assegnare a particelle piccolissime in movimento, come gli elettroni, analoga doppia natura della luce: onda e particella. Supponendo vera questa idea, se ad un’onda, avente una determinata lunghezza d’onda, è possibile associare una quantità di moto…. …sarà possibile ad una particella, avente una determinata quantità di moto, associare una lunghezza d’onda. I passaggi matematici per ricavare il valore di questa lunghezza d’onda sono semplici: Considerando che Einstein, dato l’effetto fotoelettrico, aveva associato alla luce una quantità di moto mc=h/λ e considerando v la velocità elettrone (al posto di c) avrò λel= h/mv che rappresenta la lunghezza d’onda associata al all’elettrone in movimento ondulatorio. Naturalmente era solo un’idea. Occorrevano prove sperimentali certe, per ammettere che l’elettrone si comporti davvero come un’onda. La strada era una sola: Young nel 1801 aveva dimostrato il comportamento ondulatorio della luce grazie al fenomeno della diffrazione della luce e dell’interferenza a bande alternate dei fasci provenienti da due fenditure. Occorreva osservare fenomeni analoghi per i raggi catodici (elettroni). Eseguiti gli esperimenti, i risultati furono sorprendenti: i raggi catodici davano diffrazioni e interferenze paragonabili a quelle della luce! Gli elettroni si comportano come i fotoni! Interferenza da due fessure Diffrazioni da un foro su un foglietto di alluminio Raggi X Raggi catodici Significato dell’idea di De Broglie Partiamo dallo studio del comportamento di onde più alla nostra «portata». Quando diamo uno scossone ad una corda libera, si genera un’onda che «viaggia» lungo la corda fino all’altro estremo libero per poi «scomparire». Se lo facciamo su una corda fissata all’estremità, l’onda non scomparirà, ma rimbalzando, tornerà verso la mano. Se diamo una serie di scossoni con una determinata frequenza, le onde di «andata» si incontreranno con quelle di «ritorno». Si avranno punti in cui l’interferenza sarà costruttiva (in fase) alternati a punti dove sarà distruttiva (opposizione di fase). NODI Se la frequenza e l’ampiezza degli «scossoni» si mantengono costanti, data la loro uguaglianza, le onde si incontreranno negli stessi punti e negli stessi modi: si generano onde stazionarie. Oscillazioni, cioè, che non si propagano sulla corda, ma mantengono la stessa posizione. In particolare ci saranno punti, detti nodi (oltre agli estremi) assolutamente fermi e ventri oscillanti. Se fissiamo e tendiamo una corda tra due estremi fissi (ad es. la corda di una chitarra) avremo un risultato migliore: «pizzicando» la corda, data la sua elasticità, si genera una serie di onde che, rimbalzando da un’estremo all’altro, produrranno, per interferenza reciproca, onde stazionarie. C’è un altro aspetto importantissimo, legato alla velocità delle onde generate dalla «pizzicata». Se questa ha un valore basso, l’onda stazionaria avrà una grande lunghezza d’onda, al massimo, però, λ=Lc con assenza di nodi intermedi. Se la velocità delle onde della «pizzicata» aumenta, la λ dell’onda stazionaria diminuisce e, di pari passo, compaiono e aumentano i nodi intermedi che si dispongono sempre a distanze tra loro uguali In tal modo un’onda stazionaria può avere lunghezze d’onda sempre e solo sottomultiple di quella più grande (dipendente, a sua volta, dalla lunghezza della corda su cui è generata) λn=Lc/n La serie di onde stazionarie così ottenute viene definita serie delle armoniche. Torniamo al nostro atomo Se consideriamo l’elettrone «vincolato» su una corda circolare (orbita), la cui lunghezza sarà Lc =2πr, il suo presunto movimento ondulatorio produrrà onde stazionarie aventi λn= 2πr/n. Come per il discorso delle armoniche, quindi, le lunghezze d’onda possibili saranno solo e sempre sottomultiple. Ora, assegnando al moto ondulatorio dell’elettrone λ n = h/mvn , confrontando le due equazioni 𝒉 ottengo h/mv=2πr/n. Da questa ricavo mvr= 𝒏 2π Ma questa equazione è quella posta come condizione da Bohr per spiegare le righe spettrali dell’idrogeno! Conclusione All’elettrone sono permessi ben definite (quantizzate) orbite con 𝒉 momenti angolari mvr= 𝒏 2π perché si muove come onda attorno al nucleo e genera onde stazionarie le quali, per loro natura, possono avere lunghezze d’onda precise: tutte sottomultiple della lunghezza dell’orbita λn= 2πr/n Dalle onde agli… orbitali L’imprevedibilità del comportamento dell’elettrone. Riprendiamo le esperienze sui raggi catodici: Le figure di diffrazione attraverso fori piccolissimi si ottengono sia proiettando fasci di elettroni, sia proiettandoli uno ad uno sequenzialmente. Diffrazione attraverso un foro su foglio di alluminio Raggi X Raggi catodici (1) Interfaccia, (2) alimentatore per alta tensione (3) tubo per diffrazione degli elettroni (4) webcam Nel caso dell’interferenza la situazione ha addirittura dell’incredibile: ogni elettrone sembra «sdoppiarsi», passare da entrambe le fessure per poi ricombinarsi. Solo in questo modo è possibile spiegare le figure di interferenze a bande alternate, come quelle delle onde elettromagnetiche. Approfondiamo e cerchiamo di capire meglio. Agendo sulla tensione elettrica (voltaggio) del circuito, è possibile variare la velocità di emissione degli elettroni. Con velocità opportunamente bassa si può seguire nel tempo cosa succede su uno schermo sensibile, man mano che vi giungono gli elettroni. (La cosa risulta molto più difficile con la luce, data la sua altissima velocità) tempo - + A determinati intervalli di tempo, si potrà osservare qualcosa come nelle seguenti figure V Ripetendo l’esperienza, le posizioni degli elettroni cambiano, ma non cambierà il risultato finale: zone più dense alternate a zone meno dense. Stesso risultato si osserva se gli elettroni si proiettano a fasci, anziché singolarmente. t1 10 e- t2 200 e- t3 6000 e- t4 40000 e- t5 140000 e- Il trucco svelato Le figure ottenute si spiegano come il risultato della diversa posizione assunta dai vari elettroni via via che giungono (uno alla volta) sullo schermo: non c’è nessuno «sdoppiamento»! C’è un fatto strano, però: la posizione di ogni elettrone risulta casuale, imprevedibile, diversa ogni volta che si ripete l’esperienza, impossibile da conoscere, prima del suo arrivo sullo schermo stesso. Risulta persino impossibile sapere quale delle due fessure possa attraversare, quindi fare previsioni esatte sulle traiettorie. Tuttavia, osservando meglio le figure… qualcosa è possibile determinare! la distribuzione delle «posizioni» sullo schermo non sembra, poi, del tutto casuale: esistono zone più dense e zone meno dense. Allora possiamo parlare di probabilità maggiori o minori di trovare l’elettrone, una volta «sparato», in determinate zone o punti dello schermo e, quindi, di traiettorie più e meno probabili che esso può seguire. Rappresenta i risultati della diffrazione attraverso una fenditura La disposizione di tali zone, inoltre, ricalca fedelmente la posizione delle bande alternate delle onde elettromagnetiche quindi tale disposizione può essere «matematizzata» attraverso funzioni d’onda. Una funzione d’onda, relativa alla distribuzione degli elettroni sullo schermo dopo diffrazione o interferenza, descrive matematicamente la disposizione sullo schermo di moltissimi elettroni, quindi rappresenta un fenomeno collettivo… Ma quale significato può avere una funzione d’onda per il singolo elettrone? Esistono diverse interpretazioni: Interpretazione statistica (Max Born e Einstein) La funzione d’onda è applicabile ad un insieme di particelle e ne rappresenta l’andamento statistico, collettivo. É perfettamente inutile, insignificante riferire la funzione alla singola particella. Interpretazione di Copenaghen o probabilistica (Bohr e Heisemberg) La funzione d’onda rappresenta tutte le possibilità (traiettorie e posizioni) di ogni singola particella. Tuttavia l’atto della rilevazione (misura) in un determinato istante mi permette di conoscere una sola di queste possibilità. Per capire Quando “sparo” un elettrone, posso prevedere che arriverà sullo schermo in una delle numerose possibili posizioni ricavate dallo sviluppo della funzione d’onda, posso indicare dove ha più probabilità di giungere, ma non posso sapere esattamente, con certezza assoluta il punto d’arrivo. Ancora se, dopo averlo sparato, rilevo una posizione sullo schermo e ne traccio la traiettoria seguita, non è detto che, ripetendo l’esperienza, alle stesse condizioni, venga seguita la stessa traiettoria per ritrovare l’elettrone nella medesima posizione sullo schermo. Potrebbe benissimo percorrere, in modo del tutto casuale e indipendente, un’altra traiettoria, pur tra quelle rispettanti la funzione d’onda (e sono molto numerose!) Queste ed altre interpretazioni, alternative o discendenti dalle prime due, concordano sul fatto che: Non è possibile «localizzare» il singolo elettrone che, per tal motivo, viene definito un’entità delocalizzata (o Non-localizzata) non ha, o non è possibile individuare per esso, un «luogo» fisico di esistenza definito. Heisemberg tradusse il concetto di delocalizzazione dell’elettrone nel famoso Principio di Indeterminazione Fine modello deterministico Inizio modello probabilistico Al di là dell’aspetto matematico, possiamo convincerci di tale principio analizzando la seguente situazione: Per rilevare un qualsiasi oggetto occorre utilizzare la «luce». La luce, interagendo con l’oggetto, ne subisce una (riflessione, rifrazione, diffrazione ecc.) Raccogliendo e interpretando il segnale «modificato», riusciamo a « A sua volta anche l’ » l’oggetto e le sue proprietà. , interagendo con la luce, ne subisce una Il segnale ricevuto, perciò, mi dà informazioni risultanti dall’impatto, quindi dalla reciproca modificazione: dire quanto l’informazione sia fedele alla realtà assoluta, immodificata dell’oggetto. Così, ad esempio, non potremo sapere con assoluta certezza la nè come essa sia stata modificata. Possiamo solo dichiarare (con una certa probabilità) che in un dato momento abbiamo «visto» delle della particella. Per ovviare al connesso all’« », possiamo pensare di utilizzare segnali di luminosi a modo da causare un disturbo trascurabile all’oggetto, il che ci garantirà informazioni abbastanza fedeli alla realtà. in L’idea è ottima, ma è tutt’altro che facile da realizzare con le particelle! Consideriamo una palla da basket che rimbalza nel buio Possiamo disporre di una fotocamera dotata di flash e fare una sequenza di foto in modo da «seguire» il moto della palla La luce del flash che colpisce ogni volta la palla ha lunghezze d’onda (visibili) molto più piccole delle dimensioni della palla e, interagendo con essa, riflette in modo perfetto e torna alla fotocamera in cui è posto il sensore che rileva e registra il segnale. Osservando le varie «riprese» possiamo riscostruire le posizioni, la traiettoria, calcolarne la velocità, la quantità di moto ecc. Siamo «sicuri» che tutte le caratteristiche individuate siano fedeli praticamente al 100% alla realtà in quanto l’interazione tra palla e luce è trascurabilissima. Infatti, l’energia contenuta nei segnali del flash, a confronto con quella della palla, è decisamente trascurabile (basta pensare a E=mc2 che rappresenta l’energia contenuta nella massa della palla: una quantità davvero enorme). [Come dire …. la luce non fa nemmeno il solletico alla palla!] Molto diversa è la situazione per l’elettrone: La sua massa e le sue dimensioni sono molto piccole! Date le dimensioni dell’elettrone, per «vederlo» non è possibile utilizzare luce con λ dello spettro del visibile come per la palla (nell’ordine medio dei 500 nanometri). Occorre utilizzare raggi γ (con λ intorno ai picometri) che, per converso, hanno altissime energie. Se voglio osservare con precisione la particella, dovrò utilizzare λ piccole in modo da essere riflesse o diffratte dalla particella ed essere rilevate dagli strumenti. Data la massa piccolissima dell’elettrone, da una parte, e le alte energie di tali onde, dall’altra rischio di interagire eccessivamente, quindi di modificarne le proprietà in modo significativo. (basta pensare all’effetto fotoelettrico in cui la luce visibile è in grado di spostare l’elettrone dalla sua orbita naturale) Per evitare modifiche all’oggetto, dovrò utilizzare luce a bassissima energia (λ grandi) rischio di non «vedere» la particella stessa: le onde la oltrepasserebbero senza interagire significativamente (non avrò riflessione o diffrazione apprezzabile) Occorre giungere ad un compromesso: utilizzare λ che, da una parte, consentano di «vedere» la particella quanto più nitidamente possibile, dall’altra interagiscano con essa in modo non eccessivo per non cambiarne significativamente le caratteristiche e il comportamento. Appare chiaro, ora, che quanta più precisione pretendo nel rilevare la sua posizione in un dato istante, tanto più saranno l’interazione e la modifica indotta, quindi tanto meno conoscerò il suo reale comportamento (es. la quantità di moto) Viceversa: quanto più preciso voglio essere nel determinare il comportamento (es. quantità di moto) tanto meno dovrò interagire con essa, quindi tanto meno nitida è più confusa (diffratta) sarà la sua immagine, incerta la sua posizione. λ λ Dimensione λ troppo grandi passano attraverso la particella, senza «vederla» ne spostarla. Dimensione λ troppo piccole, riflettono in modo preciso sulla particella ma ne «modificano» eccessivamente la posizione. λ Dimensione λ prossime alle dimensioni della particella, si diffrangono, riflettono in modo impreciso sulla particella e ne provocano un lieve spostamento Questa situazione fu esposta matematicamente da Heisemberg con la seguente equazione Er(x)+Er(v)=1 Er(x) Er(x) = errore minimo nella misura della posizione (x) Er(v) = errore minimo nella misura della velocità (v) Seguendo il grafico osservo che… abbassando l’errore Er(x) si alza quello Er(v) e viceversa. 1 1 Er(v) L’equazione d’onda di Shroedinger Shroedinger, dalle osservazioni di Heisemberg e dall’idea di De Broglie, riuscì ad ottenere matematicamente una complessa funzione d’onda per rappresentare tutte le possibili posizioni assunte attorno al nucleo, nel tempo, da un qualsiasi elettrone tenendo conto di tutti i 4 numeri quantici dell’atomo quantistico di BohrSommerfeld (livelli energetici, sottolivelli, numeri quantici magnetici e di spin) . Per curiosità, solo per curiosità, si riporta la formula con la simbologia specifica. Ciò che è importante è lo sviluppo matematico di tale funzione per il parametro ψ2 (psi al quadrato). Questo sviluppo (calcolando ψ2 per tutte le combinazioni dei numeri quantici di cui sopra) porta a risultati rappresentabili graficamente, su un piano tridimensionale, con zone di densità variabile (qualcosa di simile a nuvole, con parti più dense e parti meno dense). Tali zone furono nominati ORBITALI ATOMICI. Per Shroedinger ogni orbitale rappresenta la distribuzione della carica elettrica dell’elettrone zone più dense=zone più cariche (in linea con la Non-locabilità dell’elettrone) Per Bohr rappresenta la zona di probabilità di trovare l’elettrone in un dato momento zone più dense=zone più probabili (in linea con l’idea che l’elettrone sia una particella locabile) Orbitali atomici Se facciamo un confronto con l’idea originaria di De Broglie, dovremmo pensare ad un onda stazionaria vibrante non su una corda circolare, bensì su una sfera (passare da una rappresentazione bidimensionale a quella tridimensionale il «salto» di immaginazione è davvero arduo!) Per gli orbitali, risultanti dalla risoluzione della funzione d’onda ψ2 … la grandezza dipende dal numero quantico principale n la forma dipende dal numero quantico secondario l l’orientamento nello spazio dal numero quantico magnetico m Molti fisici e chimici anziché i valori numerici, al numero quantico secondario l preferisco assegnare le lettere s,p,d,f mentre per i valori del numero quantico m lettere varie come x,y,z,k,q ecc. Ogni orbitale possiede una ben determinata (quantizzata) energia che dipende solo dai primi due numeri quantici (n, l) e rispetta l’ordine seguente: I valor di energia sono correlati in modo inverso con le probabilità di ospitare elettroni. En. n 1<2<3<4<5<6<7 Prob. n 1>2>3>4>5>6>7 En. l s<p<d<f Prob. l s>p>d>f Orbitali atomici considerando il numero quantico secondario l (forma) e quello magnetico m (orientamento nello spazio) Orbitali atomici considerando tre numeri quantici (n, l, m) CONFIGURAZIONE ELETTRONICA Tenendo conto dei numeri quantici, delle interazioni elettromagnetiche e delle energie, quindi delle probabilità in gioco, nonchè dello sviluppo dell’equazione di Shroedinger, i vari elettroni tendono a disporsi attorno al nucleo, nei vari orbitali, secondo una configurazione che segue alcune regole: Regola dell’aufbau (dal tedesco «a strati») Gli elettroni tendono a sistemarsi negli orbitali a partire da quelli del livello energetico più basso (più probabile, più vicino al nucleo) a quello più alto (meno probabile, più lontano dal nucleo). Tale regola, troppo generale è, però, meglio rappresentata dalla regola della diagonale la quale, basata sullo sviluppo dell’equazione di Shroedinger, tiene in considerazione anche di qualche orbitale di un dato livello che risulta avere più energia, meno probabilità, di quelli del livello o dei livelli superiori. Principio di esclusione di Pauli In un orbitale (sottolivello) con un determinato orientamento (numero quantico magnetico m) può ospitare al massimo 2 elettroni che devono avere spin antiparallelo Principio della massima distribuzione di Hund Gli elettroni all’interno di un sottolivello tendono a sistemarsi occupando quanti più orbitali degeneri possibili (orbitali degeneri=orbitali aventi stessa probabilità, stessa energia) Solitamente la configurazione elettronica di un atomo può essere rappresentata tramite simboli alfanumerici… …o con un diagramma a caselle e freccette Rappresentazione della configurazione elettronica L’atomo di Shroedinger e i suoi orbitali I numeri quantici dell’atomo quantistico di Bohr –Sommerfeld ( livello energetico n, sottolivello l, numero quantico magnetico m, numero quantico di spin s) rimangono validi, ma non si ammettono più orbite (traiettorie) per l’elettrone. Al loro posto si parla di orbitali. Per lo stesso Shroedinger ogni orbitale ψ2 rappresenta semplicemente la distribuzione nello spazio attorno al nucleo della carica negativa dell’elettrone: più densa è la zona, più concentrata è la carica in tale zona e viceversa. Per Heisemberg e Bohr ogni orbitale ψ2 rappresenta la distribuzione nello spazio delle probabilità di trovare l’elettrone in un dato momento attorno al nucleo: nelle parti più dense è maggiore. Ad esempio, che lo sviluppo di ψ2 per l’unico elettrone dell’idrogeno permette di ottenere risultati moltissimo addensati a formare una sorta di circonferenza attorno al nucleo con raggio circa 0,5 Angstron. Il dato combacia con il valore del raggio della presunta orbita trovato anni prima da Bohr. Questo rafforzò l’opinione che a quella distanza è altissima (più del 90%) la probabilità di trovare l’elettrone in un dato istante o, nell’idea di Shroedinger, è densissima la sua carica negativa. Relativamente al nucleo e alle altre particelle subatomiche… nessuna novità sostanziale: Z numero atomico=numero di protoni (identificativo della specie atomica) A numero di massa= somma dei protoni e dei neutroni I raggi protoni e neutronici manifestavano analoghi comportamenti ondulatori e indeterministici dei raggi catodici. Il nucleo mostrava equilibri precari (radioattività) e contenuti energetici enormi (energia nucleare). Nessuna ipotesi degna di rilevanza circa l’organizzazione, la struttura e gli equilibri all’interno del nucleo fino al 1964, quando fu ipotizzata l’esistenza dei quarks Modello Standard Dalton 1803 Thomson 1904 Rutherford 1911 Bohr 1913 Sommerfeld 1916 De Broglie 1924 Modello standard 1967/68 Shroedinger 1926 Qualche riflessione… L’atomo quantistico di Bohr-Sommerfeld ricorre ad una teoria che oggi definiamo semi-classica in quanto le leggi utilizzate erano in sostanza quelle della meccanica classica, quella cioè di Newton-Maxwell (definita deterministica), con l’aggiunta di condizioni quantistiche. L’atomo di De Broglie-Heisemberg-Shroedinger ricorre a leggi nuove: quelle della meccanica quantistica (o ondulatoria o probalistica) che non è deterministica (pensate alla «delocalizzazione» dell’elettrone …!). Le teorie della fisica quantistica hanno rivoluzionato il modo di concepire la realtà e risultano sconvolgenti non tanto per la non applicabilità della meccanica classica di Newton-Maxwell (ritenuta tutt’ora valida per il mondo macroscopico) al mondo sub-atomico, quanto per le implicazioni della non-locabilità di ciascuna particella e del suo stato fisico inteso come il risultato di specifiche combinazioni probabilistiche, tra numerose possibili. • Così, ad esempio, è incomprensibile che un oggetto come una palla, di cui si possono determinare e prevedere, con assoluta certezza, posizione, velocità, peso, colore ecc… sia completamente costituita da particelle non localizzabili, il cui stato non è determinato, se non nel solo momento della loro osservazione. • E’ anche sconvolgente sapere che un oggetto e il suo stato chimico-fisico siano solo il risultato di una serie di combinazioni casuali tra le tantissime possibili. Shroedinger, per far capire a colleghi e studenti la «portata» inquietante di questa rivoluzione scientifica, che prevede l’indeterminabilità di un evento particellare, ideò un esperimento concettuale (irrealizzabile praticamente) Sostanza radioattiva: emette 1 particella/ora Dopo un’ora, il gatto è vivo o è morto? Dato che non è possibile determinare con esattezza se la particella sia stata emessa o no, occorre valutare l’evento in modo statistico: lo sviluppo del calcolo probabilistico (La funzione ψ) porta ad affermare che: gatto vivo e gatto morto non sono condizioni fisiche esistenti allo stato puro, bensì sono perfettamente miscelati, quindi la risposta esatta è… Gatto vivo/morto. La particella colpisce la leva che «scatta» in giù Cianuro La leva fa cadere il martello La fiala si rompe Einstein non era per niente d’accordo con queste convinzioni indeterministiche della realtà. Di lui rimase una frase storica: «Dio non gioca a dadi!» Mentre pare che, avvertendo vicinissima la fine della sua vita, abbia dichiarato che l’unico rammarico era quello di… non aver avuto abbastanza tempo per capire come Dio abbia creato il mondo!
Scaricare