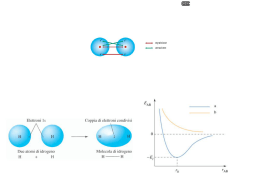
Materiali per l’Ottica
A.A. 2014/2015
Maria Antonietta Ricci
Dipartimento di Scienze, Università Roma Tre
Materiali per l’ottica: Corso di Laurea in Ottica e Optometria
Recapiti
Orario ricevimento: sempre, previo appuntamento
Telefono: 06573337226
Email: [email protected]
WEB:http://www.fis.uniroma3.it/liquidsgroup
Indirizzo: Laboratorio Fisica dei Liquidi, st.147, Via della Vasca Navale 84.
Materiali per l’ottica
Introduzione
Dal catalogo di una lente oftalmica…
Qual’e’ l’impatto delle caratteristiche
micro/macroscopiche dei materiali sulle
prestazioni di una lente oftalmica?
•Proprietà e loro caratterizzazione
•Fabbricazione
Materiali per l’ottica
Un decalogo
LA LENTE OFTALMICA IDEALE
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
Elevato indice di rifrazione (lenti meno curve)
Basso peso specifico (lenti leggere)
Alta costringenza (miglior immagine, numero di Abbe)
Resistenza alla flessione (infrangibili)
Durezza (antigraffio)
Possibilità di colorazione del materiale (lenti scure)
Possibilità di trattamenti superficiali (antiriflesso)
Inattaccabilità ai solventi (facile pulizia, lunga vita)
Stabilità meccanica e lavorabilità (andranno pur montate…)
Economicità (andranno pur vendute…)
Per capirne un pò di più studieremo:….
Materiali per l’ottica
….la relazione tra struttura e proprieta’ di un materiale
e i processi di fabbricazione….
1.
2.
3.
4.
Macroscopico
Microscopico
Atomico
Sub-atomico
Materiali per l’ottica
Legami molecolari
•
•
•
•
Ionico
Forti
Covalente
Van der Waals  0.1 eV
H idrogeno  <0.5 eV
• Ionico
NaCl
Na L 3s1 Cl L 3s2 3p5
Tra atomi a simmetria circa sferica  non direzionale
1/r
1-5 eV
Legami molecolari
•
•
•
•
Ionico
Forti
Covalente
Van der Waals  0.1 eV
H idrogeno  <0.5 eV
1-5 eV
• Covalente
H2
Legame direzionale
H 1s1
• Van der Waals
Interazione tra momenti di dipolo
V~1/r 6
forza dipolo permanente-dipolo permanente (o forza di Keesom)
forza dipolo permanente-dipolo indotto (o forza di Debye)
forza dipolo indotto istantaneo-dipolo indotto (o forza di dispersione di London)
presentano anisotropia
Sono circa 100 volte piu’ deboli dei legami covalenti
• Idrogeno
Un protone tra due atomi…
l legame idrogeno o ponte idrogeno è un caso particolare di
interazione fra dipoli. In particolare si tratta di un legame dipolo
permanente - dipolo permanente in cui è implicato un atomo di
idrogeno coinvolto in un legame covalente con elementi molto
elettronegativi (come fluoro, ossigeno, azoto), i quali attraggono
a sé gli elettroni di valenza, acquisendo una parziale carica
negativa (-) lasciando l'idrogeno con una parziale carica positiva
(+).[1] Il legame a idrogeno si forma quando la parziale carica
positiva dell'idrogeno viene in contatto con un doppietto
elettronico di un elemento fortemente elettronegativo (fluoro,
ossigeno o azoto), il quale lega l'H (che viene definito accettore,
invece l'elemento dove è legato l'H viene definito donore).
Capitoli: 1
Livelli di energia molecolari
Transizioni tra livelli di energia degli elettroni corrispondono a energie nella banda
UV e ottica (elettroni ottici) o nel range dei raggi X (elettroni di core).
etano σ → σ* a 135 nm (visibile, UV)
Livelli di energia molecolari
Transizioni tra livelli di energia vibrazionali nell’IR
Livelli di energia molecolari
Transizioni tra livelli di energia rotazionali nell’FIR e microonde
Bande di energia nei solidi
Stati elettronici nei solidi: bande elettroniche
OCCUPAZIONE DEI LIVELLI A 0 K: CLASSIFICAZIONE DEI SOLIDI
METALLI
Cu N elettroni in 4s
La banda 4s ne puo’
contenere 2N
Materiali per l’ottica
SEMIMETALLI
Mg 2N elettroni in 3s
Le bande 3s e 3p
sono sovrapposte e
2N elettroni sono al
disotto di Ef
ISOLANTI
SEMICONDUTTORI
Stati elettronici nei solidi: stati di impurezza in isolanti e
semiconduttori
Un’impurezza pentavalente, come
l’antimonio, dona un elettrone
libero
Un’impurezza trivalente, come il
crea una buca
Stati elettronici nei solidi: stati di impurezza in isolanti e
semiconduttori
Interazione tra tipo idrogeno con potenziale coulombiano schermato dal mezzo .

1 e p
U (r )  
4 r

L’eq. Di Schroedinger ammette soluzione
 E
 Ry
E 


n
n
2
0
2
0
n
0
2
2
2
Rydberg= 13.59… eV
Le impurezze nei cristalli inducono stati elettronici discreti all’interno della gap: in
un modello tipo-idrogeno hanno energia
E E E
imp
Materiali per l’ottica
c
n
Stati elettronici nei solidi: stati di impurezza in isolanti e
semiconduttori
Materiali per l’ottica
Capitoli: 2, 18
10-15
m
nucleo
10-10
m
atomo
10-9 m
macromolecola
mitocondrio
10-8
m
10-7
m
cellula
Al di sotto di 10-7 m
dobbiamo cambiare la
sonda e le lenti
106m
granello di sabbia
104m
Onde in un liquido
Vengono generate delle onde
da
sinistra verso destra:
1) Dall’ apertura posta sulla parete
nascono delle onde di forma
sferica (diffrazione)
2) Le onde sferiche generate dalle
aperture A e B danno luogo a
una serie di massimi e di
minimi
(interferenza)
A
B
•
•
•
Principio di Huygens-Fresnel, le fenditure si
comportano a loro volta come sorgenti di onde piane
sferiche coerenti con la stessa fase iniziale.
Ampiezze costanti (trascuriamo la variazione di
ampiezza dovuta alla diverse distanze tra le fenditure
e l’osservatore)
Trascuriamo la larghezza delle fenditure
d sin = m con
m = 1,2,3,...
2d sin = m con
m = 1,2,3,...
identification and quantitative analysis of
phases
Quarz
e.g. mineral phases
SiO2
SiO2
SiO2
3Al2O3 2SiO2
e.g. metals, alloys
Cu-Sn, Ag-Cu, Sn-Pb
quartz
cristobalite
glass
mullite
Mullite
Quarz+Mullite
k
k’
q
E=E’
k=k’
D2O
H2O
HDO
In che differisce un vetro da un liquido?
Richiamo: transizioni di fase
L’acqua
Ad una data pressione esiste una temperatura definita alla quale il sistema
cambia fase (Temperatura di transizione). Durante la trasformazione il sistema
scambia con l’ambiente un calore latente Hf
Materiali per l’ottica