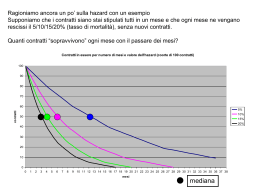
Un esempio: durata di un contratto telefonico (1000 contratti)
Durata del contratto secondo un tempo assoluto
5
Evento iniziale:
stipula
oggi
Durata ??
Contratto n.
4
3
2
1
Evento finale:
Disdetta
Durata: mantenimento del contratto
0
1998
2000
2002
2004
2006
anni
2008
2010
2012
Durata del contratto secondo un tempo relativo
5
???????
Contratto n.
4
3
2
1
0
1
2
3
4
5
anni di contratto
6
7
8
Contratti disdetti e mantenuti per mesi di durata (valori assoluti)
69
65
61
57
53
mesi di durata del contratto
49
45
41
Disdetti
37
Mantenuti
33
29
25
21
17
13
9
5
1
0
5
10
15
20
numero di contratti
25
30
35
Versione semplificata: tempo in anni
Disdette del contratto secondo gli anni di abbonamento
6
durata abbonamento = numero di anni
5
4
disdetti
in corso
3
2
1
0
20
40
60
80
100
numero utenti
120
140
160
180
I contratti in corso sono tipicamente delle OSSERVAZIONI CENSURATE
Di questi contratti sappiamo che non sono stati disdettati ad “OGGI” e che sono
stati stipulati nel mese precedente l’”OGGI”
Cioè che il loro tempo di durata t è  ad una certa soglia T
Qui nasce il primo problema sul tempo continuo/discreto:
Per quanto rendiamo piccolo l’intervallo temporale considerato, (qui è un mese)
esso rimane SEMPRE un INTERVALLO
Il che significa che noi classifichiamo come appartenente al mese m anche chi
stipula il contratto l’ultimo giorno e consideriamo come disdetta nel mese m+1
anche le disdette che avvengono il primo giorno del mese m+1
Poiché siamo interessati ad una probabilità, abbiamo il problema di definire quale
sia l’insieme dei casi possibili, cioè la popolazione a rischio.
Dobbiamo in qualche modo trattare il problema dei censurati, naturalmente con
qualche ipotesi (ad esempio una ipotesi di omogeneità, immaginando che nuovi
contratti siano stipulati in una stessa quota tutti i giorni del mese)
Organizziamo i dati:
Mesi di contratto
Ampiezza intervallo
Pop. inizio intervallo
Non disdetti
Disdetti
Pop. Fine intervallo
Esposti al rischio
Prop. Disdetti
Prop. Mantenuti
Prop. Sopravviventi
Densità sopravviventi
Hazard Rate
t(i)
b(i)
n(i)
c(i)
u(i)
0-12
12-24
24-36
12
1000
70
100
12
830
117
64
12
649
120
47
12
482
111
30
12
341
133
23
12
185
144
10
12
31
31
0
e(i)*
r(i) *
q(i) *
p(i) *
S(i) *
f(i) *
h(i) *
830
965
0,104
0,896
0,896
0,009
0,009
649
771,5
0,083
0,917
0,822
0,006
0,007
482
589
0,080
0,920
0,756
0,005
0,007
341
426,5
0,070
0,930
0,703
0,004
0,006
185
274,5
0,084
0,916
0,644
0,005
0,007
31
113
0,088
0,912
0,587
0,005
0,008
/
15,5
0
1
0,5873
0
0
Esposti al rischio
e(i)  n(i)  0.5c(i)  u (i)
r (i)  n(i)  0.5c(i)
Prop. Disdetti
q (i )  u (i ) r (i )
Pop. Fine intervallo
Prop. Mantenuti
p(i)  1  q(i)
36-48 48-60 60-72
>72
hp sui censurati (0,5 disdette)
hp sui censurati (0,5 disdette)
stima probabilità
stima probabilità
S (i)  S (i  1) p(i) S (1)  p(1) Stima ripartizione
f (i)  S (i  1)  S (i) b(i)
f (1)  1  S (i) b(i)
Densità sopravviventi
Prop. Sopravviventi
Hazard Rate
h(i )  d (i ) b(i )r (i )
Densità
Stima rischio "istantaneo"
Quantità importanti, che descrivono compiutamente la distribuzione delle durate:
Data una variabile aleatoria T (la durata) essa è descritta da:
•una densità:
f (t )
•una ripartizione F (t )  p(T  t )
Da cui si ricavano:
•Funzione di Sopravvivenza (Survival function)
Probabilità di sopravvivere almeno fino a t
S (t )  PT  t   1  F (t )
•Funzione di Rischio (hazard)
Rischio che l’uscita avvenga in t+t posto che lo stato è durato fino a t
Dove  è l’intervallo unitario
P(t  T  t  t / T  t ) f (t )
f (t )
 (t ) 



S (t ) 1  F (t )
•Hazard cumulato
(t )    (t )
i
Nel continuo sarà, data F(t):
Densità:
Sopravvivenza
Hazard
Hazard cumulata
Relazione S-H
Inizio: tempo 0
Tutti contratti stipulati = 1000
Dopo 12 mesi sono “vivi” il 90%
dei contratti = (circa) 900
Simmetricamente: per arrivare
ad a perdere (1-0.6) il 40% dei
contratti sono stati necessari
circa 5 anni
12
72
Su dati mensili:
Introduzione all’inferenza: formule di Green
i 1
q( j )
SES (i )  S (i ) 
j 1 r ( j ) p ( j )
f (i )
SE f (i ) 
b(i )
i 1
i 1
q( j )
p( j )


j 1 r ( j ) p ( j )
j 1 r ( j ) q ( j )
2

h(i )
 1
 
SEh(i ) 
1   h(i )b(i ) 
r (i )q(i )   2
 
Confronto tra gruppi
• se non ci sono censurati ususali test non parametrici (Wilcoxon, Mann Whitney)
•In presenza di censura vanno modificati (es. Wicolxon modificato da Gehan):
Due gruppi (X e Y) di numerosità nx e ny e siano:
x1 ,..., xr  X  durate non censurate
xr*1 ,.., xn*x  X  durate censurate
y1 ,..., ys  Y  durate non censurate
yr*1 ,.., yn*y  Y  durate censurate
verifichiamo l ' ipotesi
H 0 : S X (t )  SY (t )
H1 : S X (t )  SY (t )
Definiamo la quantità:
U ij  1
if
U ij  0
if
U ij  1
if
xi  y j
xi  y j
xi  y j
or
or
or
xi*  y j
xi*  y j or
yi*  x j
or ( xi* , y *j )
xi  y *j
calcoliamo
nx
ny
W   U ij
i 1 j 1
W aumenta
ogni volta che vi sono in X durate maggiori o
censure maggiori di una durata conclusa in Y
W diminuisce ogni volta che vi sono in Y durate maggiori o
censure maggiori di una durata conclusa in X
W dovrebbe tendere a 0 se è vera H0
Più precisamente:
W  N (0, V )
con
nx
V
ny
nx n y  U ij2
i 1 j 1
(nx  n y )( nx  n y  1)
W
Z 
 N (0,1)
V
NB. Ci sono diverse “scorciatoie” per il calcolo di W
Confronto tra “gruppi” (trimestrale): stato civile
Overall Comparisonsa
Wilcoxon
(Gehan)
Statis tic
11,673
df
1
Sig.
,001
a. Comparis ons are exact.
Titolo di studio:
Overall Comparisonsa
Wilcoxon
(Gehan)
Statis tic
33,241
df
4
Sig.
,000
a. Comparis ons are exact.
Pairwise Comparisonsa
(I) ed
1
2
3
4
5
(J) ed
2
3
4
5
1
3
4
5
1
2
4
5
1
2
3
5
1
2
3
4
Wilcoxon
(Gehan)
Statis tic
2,987
8,367
25,103
16,208
2,987
1,647
13,554
7,477
8,367
1,647
4,790
2,768
25,103
13,554
4,790
,003
16,208
7,477
2,768
,003
a. Comparis ons are exact.
df
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
Sig.
,084
,004
,000
,000
,084
,199
,000
,006
,004
,199
,029
,096
,000
,000
,029
,954
,000
,006
,096
,954