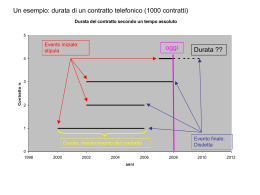
Ragioniamo ancora un po’ sulla hazard con un esempio
Supponiamo che i contratti siano stai stipulati tutti in un mese e che ogni mese ne vengano
rescissi il 5/10/15/20% (tasso di mortalità), senza nuovi contratti.
Quanti contratti “sopravvivono” ogni mese con il passare dei mesi?
Contratti in essere per numero di mesi e valore dell'hazard (coorte di 100 contratti)
100
90
80
70
contratti
60
5%
10%
50
15%
20%
40
30
20
10
0
0
1
2
3
4
5
6
7
8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38
mesi
mediana
La Hazard si comporta come un tasso di interesse composto
Se deposito 1000 euro e il tasso annuo che la banca mi paga è del 3%
Supponendo che l’interesse venga capitalizzato ogni giorno, cioè ogni giorno la
banca v mi accredita il (3/365)% di quanto avevo in conto il giorno prima
Alla fine dell’anno avrò 1.030,39 € NON 1.030 come sarebbe se l’interesse fosse
capitalizzato tutto a fine anno, perché nel corso dell’anno percepisco interessi sugli
interessi.
Se fosse
mensile avrei
trimestrale
1.030,42
1.030,34
Come si vede è l’hazard (il tasso di interesse) e la scansione temporale (discreta)
che guidano il processo
La Hazard si comporta come un tasso di interesse composto
Nell’esempio dei contratti la hazard è lievemente superiore del tasso di mortalità:
Quando il tasso è costante la relazione è
Log[S(t)]= -t
Poiché è costante si può calcolare in un punto, ad es la mediana
Questi sono i valori (approssimati):
t.m.
hazard
5%
10%
15%
20%
56%
11%
16%
22%
Naturalmente l’ipotesi di costanza dell’hazard (o del tm) è piuttosto restrittiva
Più spesso varieranno col tempo
Data la funzione di densità di T
 f(t)
t
F (t )   f ( s)ds  Pr(T  t )
Ripartizione:
0
Sopravvivenza
Hazard
S (t )  1  F (t )  Pr(T  t )
Pr(t  T  t  t / T  t )
F (t  )  F (t ) f (t )
 lim

 0


0

S (t )
S (t )
 (t )  lim
t
Hazard integrata
(t )    ( s)ds
0
Relazioni:
 d ln S (t )
 (t ) 
;
dt
f (t )  S (t ) (t ) ; S (t )  e   (t ) ; (t )   ln S (t )
Modelliamo la hazard: modello semplice = rischio costante
 d ln S (t )
 (t )   

dt

S (t )  Ket
 ln S (t )  k  t
Distribuzione esponenziale, caso piuttosto semplice infatti per la
distribuzione esponenziale è:
E (t ) 
1

1
ˆ
 
t
In generale, la hazard dipende da 2 parametri ( e p)
E la dipendenza della hazard dal tempo (positiva o negativa) è “governata” dal
parametro p e dalla distribuzione scelta:
Esponenziale
hazard costante
 (t )  
Weibull
hazard Crescente/decrescente (dip.da p)
Log-logistica
Hazard prima cresce poi cala
Lognormale
Hazard prima cresce poi cala
 (t )  p(t ) p 1
p(t ) p 1
 (t ) 
1  (t ) p 1
( p / t )  p ln( t ) 
 (t ) 
 p ln( t ) 
NB la hazard è altamente non lineare:
hazard weibull per valori di p
0,025
0,75
0,85
0,02
0,95
1,05

0,015
1,15
0,01
1,25
1,35
0,005
1,45
1,55
0
0
20
40
60
t
80
100
120
1,65
1,75
Altre distribuzioni
ln L 
NON

stima MLE tenendo conto dei dati censurati
 ln f (t /  )   ln S (t /  )
censurati
oppure dato
censurati
f (t )   (t ) S (t )
  (t /  )   ln S (t /  )
ln L 
NON
censurati
censurati
Esempio: durata in giorni di un insieme di scioperi (Green)
Esponenziale
s.e.
Weibull
s.e.
Log-logistica
s.e.
Lognormale
s.e.

p
mediana
0.02344
1.00000
29.6
0.003
0.000
3.522
0.02439
0.92083
27.5
0.003
0.111
4.00
0.04153
1.33148
24.1
0.007
0.172
4.102
0.04514
0.77206
22.2
0.008
0.089
3.95
stima hazard per sciopero
0,04000
0,03500
0,03000
0,02500
hazard
Esponenziale
Weibull
0,02000
Log-logistica
Lognormale
0,01500
0,01000
0,00500
0,00000
0
20
40
60
t
80
100
120
Introduciamo delle determinanti X.
Le determinanti vengono introdotte nel termine , naturalmente al’esponente
i  e  x
i
Si modifica la logL che ora viene minimizzata in p,  e 
Nell’esempio degli scioperi, introducendo un indice della produzione
industriale si ottiene, per la Weibull:
-ln() = 3.7772 – 9.3515 x
;
p=1.00288
=exp(-3.772+9.3515x)
Attenzione alla lettura dei coefficienti !
Occorre ricordarsi che, nella weibull
i (t )  i p(it )
p 1
 (3.77  9.35xi ) *1.002(3.77  9.35xi ) * t 
0.002
hazard esempio sciopero per diversi livelli della X (variazione indice produzione industriale)
0,04
0,035
0,03
-0,05
-0,04
0,025
-0,03
hazard
-0,02
-0,01
0,02
0
0,01
0,02
0,015
0,03
0,04
0,05
0,01
0,005
0
0
20
40
60
80
100
tempo (giorni)
Hazard quasi “piatta” infatti p quasi =1….come esponenziale
120
Ma nell’esempio dei contratti:
-ln() = 2.3314 + 0.0601 età
;
p=1.19759
hazard esempio contratti per diversi livelli della X (età)
0,05
0,045
0,04
20
0,035
25
30
hazard
0,03
35
40
0,025
45
50
55
0,02
60
65
0,015
70
0,01
0,005
0
0
20
40
60
tempo (giorni)
80
100
120
Attenzione alla lettura dei coefficienti !
In generale la Hazard adesso dipende da t, p, e X
Il segno del coefficiente della X indica la direzione dell’effetto sulla hazard
SOLO SE la hazard è MONOTONA ! (es. nelle loglog non vale!)
In ogni caso l’effetto è NON LINEARE
La interpretazione va fatta
Per valori “tipici” delle X (es.medie)
Disegnando la funzione (hazard e/o Survival)
Per strati di popolazione
Per tipologie
Analisi di specificazione:
Usuali test per stime MLE (LR, LM, WALD)
Diversi test di adattamento sono stati proposti, ma i risultati sono, in
generale, condizionati alla scelta della distribuzione di partenza.
Il problema della errata specificazione del modello, cioè della eterogeneità
non osservata è particolarmente rilevante nell’approccio parametrico e, in
generale, non ha una soluzione semplice.