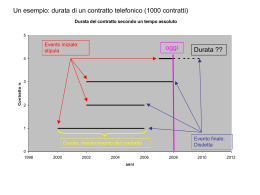
Modelli di durata : terminologia di base
Stato = caratteristica di una unità statistica che ha una estensione
temporale definita
Evento = istante temporale (di norma connesso ad un fatto) in cui
inizia/finisce uno Stato
Tempo = adeguata misura dell’estensione temporale di uno Stato
Durata = misura del periodo di tempo compreso tra un evento
INIZIALE e uno FINALE, quindi di permanenza in uno Stato
Durata del corso di studi secondo un tempo assoluto
5
Evento iniziale:
Immatricolazione
oggi
Durata ??
Sudente n.
4
3
2
1
Evento finale:
Laurea
Durata: anni di iscrizione
0
1998
2000
2002
2004
2006
anni
2008
2010
2012
Durata del corso di studi secondo un tempo relativo
5
???????
Sudente n.
4
3
2
1
0
1
2
3
4
5
anni di iscrizione
6
7
8
Per poter costruire un modello che ha al suo interno il tempo
dobbiamo preliminarmente ragionare e dedicare un po’ di “tempo”
a capire come possiamo definire e come possiamo misurare il tempo
Soprattutto dobbiamo cercare di ragionare su una sua caratteristica fondamentale:
Il tempo è continuo o discreto?????
Tanto per essere concreti, questi grafici rappresentano lo stesso fenomeno
a diverse scale temporali
Come questi:
Un problema spinoso: IL TEMPO
Un po’ di (prei) storia:
Circa 24.000 anni fa
NASCONO I PRIMI NUCLEI FAMIGLIARI (sepolture di coppie)
Circa 24.000 anni fa
DIVISIONE DEI COMPITI NELLA FAMIGLIA (sopravvive anche chi non caccia)
(in alcune tribù) COMPAIONO PER LA PRIMA VOLTA GLI ANZIANI (prima neppure sepolti)
Gli anziani non cacciano e hanno tempo per osservare, pensare e ricordare
Figure sempre più importanti nella tribù: e' infatti lui, questo anziano, a
raccogliere le molteplici notizie, i fatti; a osservare la cronologia degli avvenimenti
del mondo (e' lui libro, giornale, radio, tv , del villaggio)
E' sempre lui a ricombinare le notizie a metterle in associazione, a creare quindi
nuove strategie di organizzazione, a raccontare agli altri le storie
dei singoli, a
immagazzinare le esperienze indirette
Nasce la cultura verbale, il racconto di gesta, di felici periodi e di cose che non ha
mai visto, ma che sa che esistono, di cose che non ha mai fatto ma sa come si
fanno; e' il vecchio saggio!
SORPRESA! Le tribù con un saggio hanno un vantaggio competitivo, elaborano
strategie di sopravvivenza più efficaci, prevalgono sulle altre.
Il vecchio diventa sempre più abile ad osservare, capire e ricordare:
Guadagna carisma,diventa prima IL SAGGIO, poi LO STREGONE, SCIAMANO,
MAGO, PROFETA, SACERDOTE, (PSICOLOGO, NEUROPSICOLOGO??)
Tra le altre cose, come tutti vecchi, dorme poco:
Nelle notti, insonne, osserva il cielo fuori dalla sua caverna, scopre che ogni tanto
la luna è PIENA, capisce che questo avviene a intervalli regolari, scopre la
periodicita', afferra la nozione del tempo piu' lungo, quello oltre il quotidiano.
Allora prende un bastone e ogni notte fa una tacca (tag=giorno - in sanscrito),
dopo 28 notti, la luna e' ancora piena: e il bastone è ora diventato la misura del
tempo (mas (mese) in sanscrito e' misura)
La radice arcaica me/mas= misura segue tutte le lingue, mensis in latino,
messen in tedesco, in inglese measure e dal sanscrito mas-mon=misura luna da'
nome a luna e mese (moon-month). Ma anche a metro/mestruazioni e chissà
quanti altri
Il ns. Vecchio si accorge delle 4 fasi , una
fase ogni 7 tag (giorni- ancora in tedesco!)
Nasce cosi' la set-mas. (settimana).
Continua ad osservare, e fa una scoperta
ancora piú interessante e strabiliante:
dopo 13 mas (dopo 13 bastoni-misura) la
luna sorge esattamente dietro la stessa
collina!
Intuisce tutto, chiama tutti fuori dalla grotta ; predice che quella sera la luna
sorgera' esattamente in quel preciso punto del cielo.
Spiega, col suo bastone in mano, il fenomeno, tracciando per terra, per
farsi capire, un cerchio e cerchio-anello in sanscrito e' anu.
E' nato l'anno, l'anno lunare dei mesi (anu del mas del mon)
ETC….ETC….
Cosa insegna la storiella?
1. La forza del vecchio è l’idea di prevedere: cercare di immaginare il futuro,
implicando con ciò il primo e fondamentale elemento costitutivo dell’idea del
tempo: la tripartizione passato, presente, futuro. Non c’è idea di tempo se non
prendendo coscienza di un’aspettativa che può o non può avverarsi, in
contrapposizione ad una memoria che posso rievocare a piacimento ma non
più realizzare; l’idea, appunto, di un flusso temporale unidirezionale e
irreversibile.
2. L’arte della previsione (e la moderna scienza in questo non ha nulla di
diverso), non può che fondarsi sulla ricerca delle regolarità, delle ripetizioni
cicliche. Dunque in primo luogo quelle cosmiche: l’alternarsi del giorno e delle
notte, delle fasi lunari, delle stagioni, ecc… e, connessi con questi, tutti quei
fenomeni ciclici che, come le alternanze climatiche e i cicli vegetativi della
natura, condizionano la nostra vita sulla terra.
Sembra tutto ovvio, il fatto è che viviamo in una civiltà in cui tutto è scandito
secondo un ordine preciso e regolare, continuamente controllato da strumenti
tecnologici, che in qualche modo riassumono in sé e quasi materializzano
concetti astratti e sfuggenti come il tempo.
Il tempo ci sembra oggi talmente sotto controllo da non consentirci di vedere quali
abissi concettuali esso nasconde.
… E POI QUEL MATTO DI ZENONE…
“In ogni momento dato un corpo occupa uno spazio esattamente uguale alla sua
grandezza, e quando un corpo occupa uno spazio uguale a se stesso è in quiete.
Pertanto in ogni istante di un movimento il mobile sarà in quiete, e un movimento
non può risultare da una somma di stati di quiete.”
Il movimento è (sembra) continuo…….
….ma in ogni istante la freccia è FERMA!
… CIOE’ IL TEMPO PROCEDE “A SCATTI” ????…
In questo caso il movimento che ci appare continuo, sarebbe in realtà una specie di
montaggio di fotogrammi…
Proprio come un film, in cui il movimento è una impressione generata da una
sequenza di immagini “FISSE”
Quasi incredibile, anche se questo risolverebbe il problema di Achille e la tartaruga…
“Achille gareggia con una tartaruga che parte in posizione avvantaggiata.
Per quanto Achille possa essere veloce non potrà mai superare la tartaruga , per
quanto essa possa essere lenta.
Infatti, quando Achille raggiungerà la posizione iniziale della tartaruga, questa
sarà andata avanti coprendo una certa breve distanza; e quando Achille avrà
attraversato questa breve distanza, la tartaruga si sarà spostata un po’ più in
avanti; e così via il processo continua indefinitamente, con il risultato che il
veloce Achille non potrà mai superare la lenta tartaruga.”
Naturalmente Achille raggiunge la tartaruga
Perché la somma di infiniti termini che via via si riducono ha un valore finito:
100 + 10 + 1 + 0,1 + 0,01 + 0,001 + 0,0001 + …=111,1111
Ma questo nulla dice circa la divisibilità infinita del tempo e dello spazio, cioè sulla
loro continuità
… SE IMMAGINIAMO CHE IL TEMPO E LO SPAZIO SIANO DISCRETI , CIOE’ CHE
IL MOVIMENTO PROCEDA “A SCATTI” …
Basta immaginare che mentre la tartaruga fa uno scatto (movimento) Achille ne faccia
(per sempio) due:
… …SE AUMENTIAMO LA VELOCITA’ IL MOVIMENTO “SEMBRA” CONTINUO
OGGI
La nostra vita è regolata secondo precise scansioni temporali.
Molti orologi digitali segnano l’ora esatta continuamente regolata da un impulso
radio proveniente da una centrale situata in Germania.
Sul monitor del computer appare ancora una volta l’ora esatta.
Se le due ore non coincidono penso subito che qualcosa non funziona, perché
escludo a priori che le due ore si riferiscano a cose diverse. Controllo con una
terza fonte “sicura”.
Poi l’orologio da polso che indica, ad esempio,l’ora della lezione.
Se non trovo gli studenti in aula penso che sia successo qualcosa, ma non certo
che la mia ora sia qualcosa di diverso da quella degli studenti.
Tutto questo ci fa percepire il tempo come qualcosa di oggettivo e di molto preciso,
misurabile con approssimazioni sempre più strette, che raggiungono ormai i
miliardesimi di secondo
E IERI? NON COSI’ SEMPLICE ANZI STRAORDINARIAMENTE COMPLICATO
Ragioniamo su come si può misurare il tempo:
Supponiamo allora che si vogliano scandire i tempi di un’azione, di un evento, mediante una serie di intervalli
uguali. Tutto sommato è questa la prima fondamentale condizione perché il tempo ci appaia come una
grandezza: che un intervallo di tempo si possa confrontare con un altro.
Ma cosa significa dire che due intervalli di tempo sono uguali? Possiamo adattare le stesse esperienze che
usiamo per le lunghezze?
NO!
Se voglio spiegare il significato dell’espressione “queste due lunghezze sono uguali” devo solo prendere
un’asta che si sovrappone esattamente alla prima lunghezza e poi spostarla in modo da verificare se è
possibile sovrapporla anche alla seconda.
Per misurare intervalli di tempo, posso confrontarli solo con altri intervalli di tempo, cioè con la durata di
qualcosa che avviene esattamente in contemporanea.
Dunque se voglio confrontare la durata di un evento A con la durata di un evento successivo B, devo prima
confrontare la durata di A con un evento campione C che avviene contemporaneamente ad A. Solo che in
questo caso quando avviene B non ci sono più ormai né A né C.
Entrambi sono svaniti e appartengono ad un passato che posso evocare nella memoria ma non più rendere
presente.
L’irrevocabile annullarsi del tempo è ciò che lo rende percepibile alla nostra coscienza, perché ci
consente di separare passato e futuro, ma è allo stesso tempo ciò che lo rende evanescente
e inafferrabile.
Ma se ogni evento è divorato e annullato da quel tempo stesso che vorremmo misurare, com’è
possibile trovare un evento campione, un’unità di misura che si possa confrontare con un
evento di oggi e poi con un evento che avverrà domani quando l’oggi non ci sarà più?
Dobbiamo usare qualcosa che si ripete REGOLARMENTE CON LA STESSA DURATA!
LA CICLICITA’ DIVENTA LA CHIAVE DELLA MISURA DEL TEMPO !
l’alternarsi del giorno e della notte, il ripetersi delle fasi lunari, il succedersi regolare delle stagioni.
La ciclicità degli eventi assume allora, rispetto alla misurabilità del tempo, lo stesso ruolo che ha il
movimento rigido rispetto alla misurabilità delle distanze.
L’evento ciclico diventa il nostro regolo temporale, a condizione che i cicli si possano considerare
tutti di uguale durata. Ma non è questa la difficoltà più grossa, perché la convenzionalità di
questa assunzione non è poi molto diversa dalla convenzionalità con cui suppongo invariabile
la lunghezza del regolo durante gli spostamenti.
Il fatto è che mentre un regolo si può spostare con continuità, e quindi non è difficile porre una
sua estremità all’inizio della lunghezza da misurare, gli eventi ciclici che si presentano
spontaneamente
In natura seguono delle scansioni ben precise, per cui non possiamo ad esempio far coincidere
l’alba di questo giorno con l’inizio di un evento che avrà luogo a partire dalle 11:25.
Inoltre un regolo si può spezzare per ottenere oggetti più piccoli anch’essi utilizzabili come
regoli, mentre un evento ciclico spezzandosi dà luogo ad eventi più piccoli, ma
generalmente non più ciclici.
Così, ad esempio, il giorno, inteso come ciclo completo di 24 ore, può essere suddiviso in dì e
notte, ma queste due entità non sono tra loro, in alcun modo equivalenti o equiparabili.
Se poi andiamo a dividere ulteriormente ciascuna di queste due parti, le cose diventano ancora
più complesse. Potremmo dividere il giorno in 12 ore e la notte in 12 ore. Il guaio è che in
questo modo la durata di ciascuna ora sarà sensibilmente diversa tra notte e dì e tra estate
e inverno.
Eppure fu questo il sistema di misura usato in tutta l’antichità fino in epoca romana. La
suddivisione di una giornata in 24 ore era infatti derivata dalla civiltà mesopotamica, le ore
tuttavia non erano uguali, ma ne venivano assegnate 12 al giorno e 12 alla notte, con inizio
del nuovo giorno ad ogni tramonto. Ovviamente le ore diurne erano lunghe d’estate e brevi
d’inverno, mentre il contrario avveniva per le ore notturne.
Qui appare assolutamente chiara la convenzionalità del termine di paragone e quindi del
concetto stesso di misura. Dire che erano le ore tre dopo l’alba, significava che dal sorgere
del sole era trascorso un quarto della durata complessiva del giorno (dall’alba al tramonto),
ma non indicava nulla in termini assoluti.
Così l’anno solare non è costituito esattamente da un numero intero di giorni, l’alternarsi del
giorno e della notte varia con le stagioni, i cicli lunari hanno a loro volta una periodicità non
esattamente raccordabile con gli altri eventi ciclici.
La soluzione può essere allora di produrre artificialmente eventi ciclici il cui inizio si può
porre in corrispondenza con qualcosa d’atro. E’ il caso della clessidra e poi degli orologi.
Per misurare ad esempio il tempo concesso a degli oratori, in modo da non favorirne alcuno
rispetto agli altri, si poteva capovolgere la clessidra al momento in cui aveva inizio il
discorso. Più unità di tempo si potevano ottenere capovolgendo manualmente la clessidra
nel momento esatto in cui la sabbia era terminata.
La storia degli orologi meccanici è lunga e complessa, anche molto interessante,
Quello che però qui vogliamo notare è come nel corso della storia il tempo non si è presentato
come qualcosa di unico e di oggettivo, qualcosa che era lì e la cui misurazione era solo un
problema tecnico di maggiore o minore precisione.
Il fatto è che non vi era un solo tempo, ma una molteplicità di tempi, tra loro diversi
concettualmente e quindi non commensurabili.
Il tempo della giornata di dodici ore tra alba e tramonto era cosa ben diversa dal tempo della
clessidra o dal tempo dell’orologio ad acqua; altra cosa ancora erano il ciclo annuo e quello
cosmico misurato sui moti degli astri.
La conquista di un significato univoco nelle misura del tempo si viene a realizzare
molto lentamente nei secoli, e per tappe, da un lato con le riforme del calendario
(ricordiamo quella di Giulio Cesare e quella Gregoriana), dall’altra con il progressivo
perfezionamento degli orologi e con l’adozione del ciclo giornaliero di 24 ore.
Dare un significato univoco alla misura del tempo, non significa però conquista di un
tempo assoluto, infatti:
• l’adozione delle varie riforme non è uniforme e contemporanea in tutti i paesi,
• la diffusione degli orologi avviene con lentezza: fino a qualche secolo fa pochi ne
possedevano uno.
•Nelle campagne l’ora o la data civile servivano ben poco: il tempo continuava ad
essere scandito dai cicli naturali, secondo le necessità del lavoro dei campi
In ogni caso gli orologi andavano comunque regolati, e ciò poteva avvenire su base
astronomica, luogo per luogo, determinando per esempio l’istante in cui il sole
appariva all’orizzonte in un determinato giorno dell’anno.
Ma come coordinare gli orologi che si trovavano in luoghi diversi?
•Il problema della sincronizzazione, il peso di latitudine e longitudine.
•Segnale di sincronizzazione, velocità della luce, tempo finito, cioè discreto.
Se esiste una velocità assoluta, non superabile, allora il tempo è per forza DISCRETO
… POI CI SI METTE ANCHE LA FISICA….
Tutto prende le mosse dal tentativo di risolvere un apparente paradosso della fisica dell'epoca,
dovuto all'emissione di onde elettromagnetiche da parte di un corpo quale un forno. Seguendo le
teorie riconosciute valide, un simile corpo avrebbe propagato durante il proprio riscaldamento
onde in ogni lunghezza e frequenza possibile, la cui energia sarebbe andata aumentando
proporzionalmente a quest'ultima.
Facendo i conti risultava però che tale forno avrebbe pertanto emesso una quantità infinita
d'energia, perché infinite sono le lunghezze d'onda che si possono generare tra le sue pareti
interne ed ognuna di esse porta un contributo al totale dell'energia emessa, per quanto piccolo: la
somma di un numero infinito di addendi, qualunque sia la loro dimensione numerica, porta
comunque ad un risultato infinito.
Questo calcolo era però in evidente contraddizione con l'osservazione e con la logica, dato che
nessun forno (e nessun altro oggetto, se è per questo) emette mai una quantità infinita d'energia:
l'emergere di infiniti all'interno di una teoria fisica è sempre sintomo di qualche sua lacuna.
Questa contraddizione portò Planck ad ipotizzare nel 1900 che non tutte le lunghezze d'onda
siano in realtà possibili: solo alcune particolari configurazioni energetiche si verificano
effettivamente, e pertanto l'energia totale emessa dal corpo è pari alla somma delle sole onde
permesse. Questo costituisce un grande passo avanti, in quanto elimina l'infinito di cui parlavamo
più sopra.
Secondo Planck perciò la distribuzione delle onde possibili non è continua ma discreta, ovvero
esse non si dispongono senza soluzione di continuità lungo lo spettro delle energie possibili ma si
posizionano solo in corrispondenza di determinati punti, corrispondenti a precise lunghezze
d'onda e frequenze.
Ma l’energia è un flusso, cioè si esplica nel tempo, e quindi anche il tempo sarebbe discreto.
Zenone si vendica: aveva ragione lui????
Infatti la definizione di secondo fa riferimento all’emissione di energia:
In questo sistema discreto, il secondo è definito come la durata di 9 192 631 770 periodi della
radiazione corrispondente alla transizione tra due livelli iperfini, da (F=4, MF=0) a (F=3, MF=0),
dello stato fondamentale dell'atomo di cesio-133
“Il tempo di Planck” diventa l'unità naturale del tempo. È considerato il più breve intervallo di tempo
misurabile.
5.391 × 10−44 secondi
dove: h è la costante di Planck, G è la costante gravitazionale ,c è la velocità della luce nel vuoto
Il tempo di Planck è il tempo che impiega un fotone che viaggia alla velocità della luce per
percorrere una distanza pari alla lunghezza di Planck.
È il "quanto del tempo", la più piccola misurazione del tempo che abbia qualche significato. L'età
stimata dell'universo (4.3 × 1017 s) è di circa 8 × 1060 tP.
La lunghezza di Planck, è un'unità di misura della lunghezza, approssimativamente pari a 1,6 ×
10-35 metri. Fa parte di un sistema di unità di misura detto "Unità di misura di Planck"; può essere
inoltre definita come "unità naturale", dal momento che viene ricavata a partire da tre costanti
fisiche fondamentali: la velocità della luce, la costante di Planck e la costante di gravitazione
universale.
Dunque il tempo è “granuloso” come la materia?
Esistono quark di tempo come esistono quark di materia?
MAH, in ogni caso le nostre misure hanno un livello di risoluzione minimo fisso
Sicuramente avremo a che fare con tempi discreti
Probabilmente perché il tempo è discreto in sé…
Ma in ogni caso lo sono le nostre misure.
Vedremo che questo influirà sulla definizione della funzione di rischio!
Un esempio: contratto telefonico
Disdette del contratto secondo gli anni di abbonamento
200
180
160
140
numero utenti
120
disdetti
100
in corso
80
60
40
20
0
1
2
3
4
durata abbonamento = numero di anni
5
6
In percentuale
Disdette del contratto secondo gli anni di abbonamento
100%
90%
80%
percentuale utenti
70%
60%
Disdetti
50%
In corso
40%
30%
20%
10%
0%
1
2
3
4
durata abbonamento = numero di anni
5
6
Consideriamo (per ora) solo le disdette (274 casi su 1000)
Disdette del contratto secondo i semestri di abbonamento
120
100
numero utenti
80
60
40
20
0
1
2
3
4
mesi
5
6
Organizziamo i dati: consideriamo (per ora) solo le disdette (274 casi su 1000)
anni di contratto
Ampiezza intervallo
Abb. inizio intervallo
Non disdetti
Esposti al rischio
Disdetti
t(i)
b(i)
n(i)
c(i)
r(i) *
u(i)
Proportion Terminating
Proportion Surviving
Cum.Prop.Surviving
Probability Density
Hazard Rate
q(i) *
p(i) *
S(i) *
f(i) *
h(i) *
n(i  1)  n(i )  0.5c(i )  u (i )
p(i )  1  q(i )
f (i ) 
1
2
3
4
5
6
12
274
0
12
274
0
12
215
0
12
169
0
12
135
0
12
105
0
274
0
274
59
215
46
169
34
135
30
105
31
0
1
1
0
0
0,22
0,78
0,78
0,22
0,24
0,21
0,79
0,62
0,17
0,24
0,20
0,80
0,49
0,12
0,22
0,22
0,78
0,38
0,11
0,25
0,30
0,70
0,27
0,11
0,35
r (i )  n(i )  0.5c(i )
S (i )  S (i  1) p(i )
S (i  1)  S (i )
b(i )
f (1) 
1  S (1)
b(1)
q(i ) 
S (1)  p (1)
h(i ) 
d (i )
b(i )r (i )
u (i )
r (i )