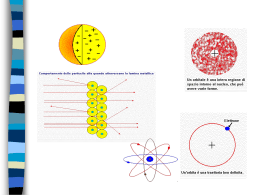
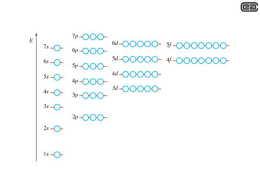
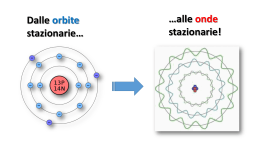
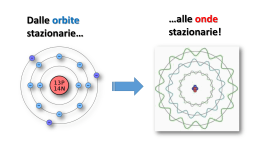
Dalle orbite
stazionarie…
…alle onde
stazionarie!
Le lacune nella teoria di Bohr
La formula di Rydberg e il modello atomico di Bohr delle «orbite stazionarie circolari»
spiegavano bene le righe dello spettro dell'idrogeno, che possiede un solo elettrone
attorno al nucleo.
Per elementi aventi più elettroni era più difficile, se non impossibile, trovare una formula
empirica delle loro righe spettrali e, quindi, un modello atomico che rappresentasse la
struttura dei rispettivi atomi.
Sommerfeld e altri avanzarono l’idea che gli elettroni disturbandosi, al fine di trovare un
equilibrio, potessero percorre anche orbite di forma ellittica con differenti orientamenti
nello spazio e che, inoltre, ciascun elettrone potesse ruotare attorno al proprio asse.
Modello di Sommerfeld-Bohr
Negli anni ‘20 del secolo scorso si propose un modello complesso in cui ad ogni elettrone furono
assegnati 4 numeri quantici:
 Numero quantico principale o livello energetico n (valori  1, 2, 3, 4, 5, 6, 7)
 Numero quantico secondario o sottolivello o forma dell’orbita l (valori  s, p, d, f)
 Numero quantico terziario o magnetico o
orientamento dell’orbita m (valori  -3, -2,
-1, 0, +1, +2. +3)
 Numero quantico quaternario o magnetico
di spin s (valori  -1/2, +1/2)
s
s
p
d
f
s
3
2
p
1
I valori possibili di l per ogni livello n.
1. l=s
2. l=s, l=p
3. l=s, l=p, l=d
4. l=s, l=p, l=d, l=f
5. l=s, l=p, l=d, l=f
6. l=s, l=p, l=d, l=f
7. l=s, l=p, l=d, l=f
Livello energetico o numero
quantico principale n
Forma dell’orbita o Sottolivello energetico o
Numero quantico secondario
l
I valori possibili di m (orientamento) per ogni l
Per l=s  m= 0
Per l=p  m= -1, 0, +1
Per l=d  m= -2, -1, 0, +1, +2
Per l=f  m= -3, -2, -1, 0, +1, +2, +3
 I valori possibili dello spin s sono sempre -1/2 e +1/2 per ogni elettrone
Il modello di Sommerfeld-Bohr, tuttavia, riusciva a spiegare solo una buona parte delle
righe spettrali, non tutte.
Per quante modifiche e correttivi si potessero inserire nelle equazioni matematiche, non si
riusciva, cioè, una equazione perfetta, quindi un modello perfetto.
Alla fine degli anni ‘20, gli scienziati dovettero rinunciare a «determinare» con precisione
assoluta il comportamento degli elettroni all’interno dell’atomo.
Heisemberg enunciò, pertanto ,il suo principio di indeterminazione
Non è possibile conoscere contemporaneamente posizione e velocità
dell’elettrone
L’elettrone fu ritenuta, quindi, una entità non localizzata: non esiste per esso un luogo fisico di esistenza definito
Fine Teoria deterministica
Inizio Teoria probabilistica
Dalle orbite alle… onde!
Pur accettando il principio di indeterminazione, non si rinunciò, tuttavia, a considerare l’elettrone come
una entità esistente e distinta da altre, perciò la ricerca scientifica proseguì per capirne meglio la natura e
le proprietà peculiari.
De Broglie, ritornando allo studio dei raggi catodici e delle relative proprietà, dimostrò che avevano molti
comportamenti analoghi a quelli dei raggi elettromagnetici: come i raggi di luce comune, i raggi catodici
potevano subire riflessione, rifrazione, diffrazione e interferenza. Quest’ultime sono caratteristiche
osservabili in tutti i fenomeni ondulatori (le onde del mare, le onde sonore ecc).
Gli elettroni, quindi, oltre a comportarsi come particelle di materia (come aveva a suo tempo dimostrato
Thomson), si comportano anche come fossero onde.
Tale comportamento dualistico assomiglia a quello dei fotoni (vedi Planck e Einstein).
Anche per gli elettroni, quindi, si può parlare di natura dualistica: sono contemporaneamente particelle e
onde.
Proprio a questa doppia natura fu imputata la non locabilità e l’indeterminazione precedentemente
ipotizzata.
Si propose, per l’atomo, un modello in cui si immaginò una serie di onde stazionarie:
onde elettromagnetiche stazionanti intorno al nucleo a ben definite distanze e con
precise frequenze ( e lunghezze) d’onda.
Dalle onde agli… orbitali
L’idea degli elettroni come onde mise fine alle pretese di poter tracciare «traiettorie», cioè orbite bel definite .
Nacque l’idea di poter almeno delimitare la zona dello spazio attorno al nucleo entro cui un elettrone esercita
in modo significativo i suoi effetti elettromagnetici (e quindi entro cui questa entità esiste)
Shroedinger, mettendo insieme le proprietà ondulatorie con i 4 numeri quantici del modello di SommerfeldBohr (che pure sono caratteristiche misurabili dell’elettrone) pervenne ad una complessa funzione matematica
la quale permise di individuare le zone di maggior probabilità di esistenza dell’elettrone.
La funzione matematica è la funzione d’onda ψ2 (psi al quadrato).
La risoluzione di tale funzione, sostituendo i vari valori dei numeri quantici permette di ottenere non precise
orbite, ma zone, chiamate orbitali, con determinate probabilità di esistenza dell’elettrone
Il concetto di orbita (traiettoria lineare dell’elettrone)
fu sostituito da quello di
Orbitale (zona di probabilità di localizzare l’elettrone)
Orbitali atomici
Il numero quantico principale n incide sulla grandezza
dell’orbitale
la forma dipende dal numero quantico
secondario l
Il numero quantico magnetico m indica
l’orientamento nello spazio dell’asse principale
dell’orbitale
Lo spin descrive un’altra proprietà
magnetica intrinseca della zona legata alla
polarizzazione dell’onda elettromagnetica.
CONFIGURAZIONE ELETTRONICA
Tenendo conto dei numeri quantici, delle interazioni elettromagnetiche e delle energie, quindi delle probabilità in gioco,
nonchè dello sviluppo dell’equazione di Shroedinger, i vari elettroni tendono ad esistere attorno al nucleo, nei vari orbitali,
secondo una configurazione che segue alcune regole:
Regola dell’aufbau (dal tedesco «a strati»)  Gli elettroni
tendono a sistemarsi negli orbitali a partire da quelli del livello
energetico più basso (più probabile, più vicino al nucleo) a
quello più alto (meno probabile, più lontano dal nucleo). Tale
regola, troppo generale è, però, meglio rappresentata dalla
regola della diagonale la quale, basata sullo sviluppo
dell’equazione di Shroedinger, tiene in considerazione anche di
qualche orbitale di un dato livello che risulta avere più energia,
meno probabilità, di quelli del livello o dei livelli superiori.
Principio di esclusione di Pauli  In un orbitale (sottolivello) con un determinato orientamento (numero quantico
magnetico m) può ospitare al massimo 2 elettroni che devono avere spin antiparallelo
Principio della massima distribuzione di Hund  Gli elettroni all’interno di un sottolivello tendono a sistemarsi
occupando quanti più orbitali degeneri possibili (orbitali degeneri=orbitali aventi stessa probabilità, stessa energia)
Solitamente la configurazione elettronica
di un atomo può essere rappresentata
tramite simboli alfanumerici…
…o con un diagramma a caselle e freccette
Rappresentazione della configurazione elettronica
Il nucleo
Z  numero atomico=numero di protoni (identificativo della specie atomica)
A numero di massa= somma dei protoni e dei neutroni
 I raggi protoni e neutronici manifestano analoghi comportamenti ondulatori e
indeterministici dei raggi catodici.
 Il nucleo mostra equilibri precari (decadimento radioattivo) e contenuti energetici enormi
(energia nucleare).
 Nessuna ipotesi degna di rilevanza circa l’organizzazione, la struttura e gli equilibri
all’interno del nucleo fino al 1964, quando fu ipotizzata l’esistenza dei quarks  Modello
Standard
Dalton 1803
Thomson 1904
Rutherford 1911
Bohr 1913
Sommerfeld 1916
De Broglie 1924
Modello standard 1967/68
Shroedinger 1926
Shroedinger, per far capire a colleghi e studenti la «portata» inquietante della rivoluzione scientifica della meccanica
quantistica, che prevede l’indeterminabilità di un evento particellare, ideò un esperimento concettuale.
Sostanza radioattiva: emette in media 1 particella/ora
Dopo un’ora, il gatto è vivo o è morto?
Dato che non è possibile determinare con
esattezza se la particella sia stata emessa o no,
occorre valutare l’evento in modo statistico: lo
sviluppo del calcolo probabilistico (La funzione ψ)
porta ad affermare che: gatto vivo e gatto morto
non sono condizioni fisiche esistenti allo stato
puro, bensì sono perfettamente miscelati, quindi
la risposta esatta è…
Gatto vivomorto.
L’osservazione diretta (apertura della scatola),
tuttavia, «manifesterà» uno dei due stati possibili
in modo casuale, non prevedibile.
Scatola chiusa
La particella
colpisce la leva che
«scatta» in giù
Cianuro
La leva fa cadere il martello
La fiala si rompe
Einstein non era per niente d’accordo con queste convinzioni indeterministiche della realtà. Di lui rimase una frase storica:
«Dio non gioca a dadi!»