Interazioni deboli
• Interazioni deboli
• Decadimento beta
• Esistenza del neutrino
• Neutrino - antineutrino
• Transizioni di Fermi e di Gamow-Teller
• Violazione della parità nelle interazioni deboli: esperimento di M.me Wu
• Misura dell'elicità del neutrino (Goldhaber, Grodzins, Sunyar)
1
Interazioni deboli
Sono interazioni che coinvolgono leptoni e quark (pertanto anche gli adroni) e che sono
normalmente “nascoste” dalle interazioni forti ed e.m. che sono più probabili. Le interazioni
deboli violano alcune leggi di conservazione (parità, isospin), pertanto sono osservabili in quei
decadimenti proibiti per le interazioni forti ed e.m. Come vedremo, sono osservabili anche in
esperimenti di diffusione.
Le interazioni deboli vengono classificate in interazioni:
1) Leptoniche: se coinvolgono solo leptoni
μ   e   ν e  νμ
μ   e   ν e  νμ
(decadimen to del muone)
2) Semileptoniche se coinvolgono leptoni e quark (cioè adroni)
n  p  e  νe
(decadimen to del neutrone)
  p  e  νe
(decadimen to della  : viola la stranezza)
π   μ   νμ
(decadimen to del pione)
3) Non leptoniche: se coinvolgono solo quark (cioè adroni)
K   π  π0
(decadimen to del K  : viola la stranezza)
K  π  π  π
(decadimen to del K  : viola la stranezza)
  p  π
(decadimen to della  : viola la stranezza)
  n  π0
(decadimen to della  : viola la stranezza)
2
IL DECADIMENTO BETA NUCLEARE
I decadimenti deboli vennero osservati per la prima volta nel decadimento beta dei
nuclei: un nucleo con un numero in eccesso di neutroni o di protoni decade in un nucleo
con un’unità in meno o in più di protoni e lo stesso numero di nucleoni totale, emettendo
un raggio b- o b+ che si rivelarono poi essere un elettrone o un positrone.
Nel decadimento non sembrava essere emesso null’altro, cioè il decadimento sembrava
essere:
A
A
ZX  Z+1Y
A
A
ZX  Z-1Y
+ b- (e-)
+ b+ (e+)
Ci si aspettava dunque una energia cinetica fissata per l’elettrone, dovuta solo alla
differenza tra le masse dei due nuclei, in quanto (trascurando l’energia di rinculo):
MX = MY + Ee = MY + Te + me
Te = MX – MY – me
(1)
Sperimentalmente invece si otteneva uno spettro continuo, il cui valore massimo soltanto
coincideva con la (1). Il principio di conservazione dell’energia sembrava violato!!!
Anche il momento angolare non è conservato (vedi dopo).
3
IPOTESI DI PAULI DELL’ESISTENZA DEL NEUTRINO
Lo spettro continuo poteva essere giustificato solo dalla presenza di un’ altra particella di
massa nulla nello stato finale:
MX = MY + Ee + En = MY + Te + me + Tn + mn
quindi l’energia dell’elettrone può assumere valori continui da un minimo di zero fino a
un massimo che corrisponde al minimo dell’energia dell’altra particella: Tn=0
(Te)max = MX – MY – me – mn
Se inoltre questa energia massima coincide sperimentalmente con la (1):
(Te)max = MX – MY – me
ne consegue che la massa della particella deve essere nulla (o meglio eventuali deviazioni
dell’energia massima misurata dalla (1) ci darebbero un limite superiore per la massa di
tale particella).
4
Da considerazioni sulla conservazione del momento angolare si possono dedurre altre
caratteristiche di questa particella “fantasma”. Prendiamo ad esempio il decadimento beta
del nucleo di trizio H3 (un protone e due neutroni) in He3 (due protoni e un neutrone) per
emissione di un b- . I due nuclei hanno entrambi spin uguali a ½ cosi come il b- (elettrone)
ed è impossibile che una particella di spin ½ fornisca due particelle di spin ½ , in quanto
dalla regola di composizione degli spin, esse possono fornire solo valori 0 e 1.
H3  He3 + bSpin
½  ½ + ½  Impossibile perchè la composizione
dà come risultato 0 o 1
La conservazione del momento angolare è garantita solo se la particella mancante al
bilancio ha spin ½. In tal caso infatti componendo tre particelle di spin ½ possiamo
ottenere una particella di spin ½ :
H3  He3 + b- + ne
½ ½
{
½
0
1
½
½  ½
½  ½ o 3/2
5
Pauli ipotizzò pertanto l'esistenza di una particella, che battezzò "neutrino" (su
suggerimento di Fermi), avente le seguenti caratteristiche:
1) carica neutra (per la conservazione della carica)
2) massa nulla (per la conservazione dell'energia)
3) spin ½ (per la conservazione del momento angolare)
4) interagisce molto debolmente con la materia (altrimenti la si osserverebbe)
Successivamente si dedusse che il neutrino doveva essere prodotto anche in altri
decadimenti, come quello del pione e quello del muone, che altrimenti non avrebbero
conservato neanche essi il momento angolare e l'energia:
π   μ   νμ
π   μ   νμ
μ   e   νe  νμ
μ   e   ν e  νμ
6
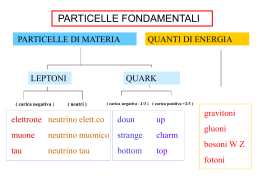
NUMERI LEPTONICI
Nelle lezione precedenti abbiamo parlato dell'esistenza delle tre famiglie leptoniche
(elettrone e ne , muone e nm , tau e nt) e della conservazione del numero quantico
leptonico associato a ciascuna delle tre famiglie.
Abbiamo anche dimostrato che i neutrini associati all'elettrone, al m e al t sono di natura
diversa, in quanto ad esempio i neutrini prodotti dal decadimento del pione:
π   μ   νμ
non possono essere adoperati per indurre la reazione seguente (beta inverso) che
richiederebbe invece un neutrino elettronico:
37
νμ  37Cl 
Ar  e
NEUTRINO  ANTINEUTRINO
Abbiamo anche dimostrato che il neutrino non coincide con l'antineutrino, pur essendo
particelle di massa nulla e carica nulla, in quanto la reazione:
νe 
37
Cl 
37
Ar  e -
non può essere indotta da un fascio di antineutrini (prodotti ad esempio da un reattore per
decadimento b nucleare di nuclei ricchi di neutroni).
7
Transizioni di Fermi - Transizioni di Gamow-Teller
Il nucleo iniziale e quello finale del decadimento beta possono avere lo stesso spin o avere
spin diversi (la differenza in tal caso può essere solo di un'unità). Infatti combinando gli
spin dell' elettrone e del neutrino nello stato finale, si avrà:

 
Seν  Se  Sν

Seν  0
1/2 [  (1)  (2) -  (1)  (2) ]


Seν  1
STATO DI SINGOLETTO
  (1)   (2)
1/2 [  (1)  (2) +  (1)   (2) ]
STATO DI TRIPLETTO
 (1)  (2)
La differenza di spin tra il nucleo iniziale (A,Z) e quello finale (A,Z+1) è fornita dalla
seguente relazione:



S(A, Z)  S(A, Z  1)  Seν


S(A, Z)  Seν
 


| S | 0  S z  0
TRANSIZIONI DI FERMI
 


| S | 1  S z   1,0
TRANSIZIONI DI GAMOW-TELLER
8
Violazione della parità nelle interazioni deboli
Fino agli anni '50 si credeva comunemente che tutte le interazioni fossero
invarianti per operazione di parità, cioè per inversione spaziale. Ciò significa
che effettuando la misura di un'osservabile fisica su un sistema o sul sistema
ottenuto invertendo le coordiante spaziali, il risultato non deve cambiare.
x, y, z

-x, -y, -z
z
y
x
-x
-y
-z
9
Il primo dubbio a proposito del fatto che le interazioni deboli potessero violare la parità fu
avanzato da Lee e Yang nel 1956, nel tentativo di risolvere il cosiddetto “tq puzzle”.
Erano stati osservati i seguenti decadimenti di due particelle aventi la stessa massa e la
stessa vita media:
q+  p+ p0
t+  p p p
Le due particelle erano state considerate diverse tra loro perchè decadono in stati finali con
parità diverse. Vediamo perchè (ricorda che la parità intrinseca del pione è (-1) e che il suo
spin è nullo, pertanto J = L + S = L):
Pπ  π 0 
  1 1 1   1
L
L
e J  L  J P  0  , 1- , 2  , ... (per L  0, 1, 2, ...)
 

L12  L 3 1
  1
e J  L12  L 3
Pπ  π  π     1 1 1 1 12 3

dove L12  momento angolare della coppia di pioni identici π  π  

L 3  momento angolare del terzo pione π   rispetto alla coppia
L L
(1)
(2)
Notiamo che L12 deve essere pari perchè la funzione d'onda del sistema ( p p )
formato da due bosoni identici deve essere simmetrico per scambio dei due bosoni 
L12=0, 2, ... Pertanto la parità del sistema dipenderà solo da L3:
Pπ  π  π     1
L 3 1
10
mentre il suo momento angolare J sarà sempre dato dalla somma di L12 ed L3:
 

J  L12  L3
Il livello più basso che possiamo costruire è quello con:
L12  L 3  0  J  0 e P  - 1
L 3 1
 1
 J P  0-
Questo stato ha lo stesso spin del sistema a due pioni ma parità opposta. Ci sarebbero altri
modi di combinare valori più elevati di L12 ed L3 che possono fornire uno stato di J-parità
uguale a uno di quelli possibili per il sistema di due pioni (1-) ma l'analisi della
distribuzione dei tre pioni nello stato finale (attraverso il cosiddetto "Dalitz plot") dimostra
che i pioni sono effettivamente in uno stato con JP = 0-.
Pertanto le due particelle decadono in stati di parità opposta. Tuttavia, a causa del fatto che
esse hanno stessa massa e stessa vita media, appariva come altamente improbabile che si
trattasse di due particelle distinte.
Lee e Yang suggerirono che in realtà si trattasse della stessa particella, che decade
debolmente (entrambi i decadimenti violano la stranezza) e che nel decadimento debole
potesse essere violata la parità. La particella che realizza i due decadimenti in questione è
il kaone positivo (K+), che ha JP = 0- e pertanto nel decadimento in due pioni con JP = 0+ è
violata la parità. Le interazioni deboli non violano obbligatoriamente la parità, ma sono
indifferenti ad essa.
11
ESPERIMENTO DI WU (VIOLAZIONE DELLA PARITÀ
DELLE INTERAZIONI DEBOLI) (continua)
In un articolo del 1956, Lee e Yang fecero osservare che fino a quel momento non erano
mai state cercate in un esperimento di interazioni deboli le prove di una eventuale loro
violazione della parità.
Essi suggerirono pertanto di fare il seguente test: osservare la dipendenza di una sezione
d’urto da un' osservabile pseudo-scalare, che è un termine che cambia segno per effetto di
una operazione di parità. Se la sezione d’urto dipende da un tale termine, cioè cambia
segno per effetto della parità, allora l’interazione viola la parità. Infatti un fenomeno
naturale sarà invariante per operazioni di parità se, applicando ad esso un' operazione di
parità (cioè osservandolo riflesso in uno specchio e rovesciato), tale fenomeno si trasforma
in un fenomeno altrettanto realizzabile in natura. Poichè osservabili pseudoscalari si
possono costruire dal prodotto scalare tra un vettore polare e un vettore assiale, un
possibile esperimento che testi tale dipendenza è un decadimento nel quale siano coinvolti
gli spin delle particelle oltre che i loro impulsi.
L’esperimento venne condotto da M.me Wu (1957) su un campione di Cobalto, che è
soggetto al seguente decadimento beta:
60Co
 60Ni* + e- + ne
60Ni
+ 
12
ESPERIMENTO DI WU (VIOLAZIONE DELLA PARITÀ
DELLE INTERAZIONI DEBOLI) (continua)
Si sceglie il Cobalto come campione in quanto
esso ha uno spin elevato (JCo=5) e può quindi
essere facilmente polarizzato. Il decadimento
in 60Ni* (JNi=4) è una transizione del tipo di
Gamow-Teller. L'elettrone è l'antineutrino
emessi nel decadimento avranno pertanto uno
spin totale pari a 1.
60Co
 60Ni* + e- + ne
60Ni
+ 
13
Il 60Co è inserito all’interno di un sale paramagnetico,
il cristallo di nitrato-cerio-magnesio. Quando al sale è
applicato un piccolo campo magnetico esterno ( 0.05
Tesla), l’orientazione dei momenti elettronici nel sale
produce un elevato campo magnetico locale
dell’ordine di 10-100 T. Con questo accorgimento è
possibile ottenere un elevato campo magnetico con cui
polarizzare il 60Co a partire da un campo magnetico
non elevato, e ciò permetterà di tenere polarizzato il
60Co
tenuto a bassa temperatura in un criostato (T 
0.01 K).
14
Qual è la variabile pseudoscalare in questione dalla quale osservare la dipendenza
del numero di elettroni emessi? I vettori in gioco sono:

p e  impulso dell' elettrone

p ν  impulso del neutrino



vettori polari

σ e  spin dell' elettrone

σ ν  spin del neutrino

σ Co  spin del 60Co

vettori assiali
Di questi vettori, solo la direzione dello spin del 60Co è nota (in quanto il 60Co è
polarizzato) e quella dell'impulso dell'elettrone è facilmente misurabile (considerate che il
neutrino non viene rivelato e per misurare la direzione dello spin dell'elettrone dovremmo
aggiungere un altro campo magnetico). L'unica osservabile fisica pseudoscalare che si può
costruire con questi due vettori è:
 
σ Co  pe
Per effetto di un'operazione di parità, come già sappiamo, lo spin del 60Co non cambia
segno, in quanto è un vettore assiale, mentre la direzione di emissione degli elettroni sì.

σ Co

pe

σ Co
P

 pe
Pertanto:
P 




 
 

σ Co  pe  σ Co pe cos θ  σ Co   pe   σ Co pe cos π - θ  σ Co  pe
15

Scopo dell' esperimento è quindi misurare la distribuzione
σ Co
degli elettroni (cioè la direzione dell'impulso) rispetto alla
e
direzione di polarizzazione del 60Co, cioè quanti degli
60Co
elettroni emessi vengono emessi nello stesso emisfero in cui
è diretta la polarizzazione del 60Co e quanti nell'emisfero
e
opposto. Una eventuale asimmetria nelle due distribuzioni
sarebbe una evidenza sperimentale della violazione di parità
da parte delle interazioni deboli, cioè affinché ci sia invarianza delle interazioni deboli
per operazione di parità sarebbe necessario che gli elettroni venissero emessi in egual
numero nei due emisferi.
Perchè? Abbiamo detto che, per effetto di un’operazione di parità, lo spin del 60Co non
cambia segno, mentre la direzione di emissione degli elettroni diventa opposta. Perchè
un sistema realmente esistente in natura si trasformi, per effetto di P, in un altro sistema
osservabile con la stessa probabilità, occorre dunque che la distribuzione degli elettroni
sia la stessa nei due emisferi:


σ Co

σ Co
pe

σ Co
P
-pe
e60Co
σ Co
P
60Co
e16
Gli elettroni del decadimento del 60Co vengono rivelati da uno scintillatore (anthracene)
che emette luce di scintillazione al passaggio di particelle cariche. La luce di
scintillazione viene raccolta e trasmessa a un fotomoltiplicatore, che la converte in
segnale elettrico.
Invece di porre due rivelatori di elettroni, uno verso l'alto e uno verso il basso, tenendo
fissa la direzione di polarizzazione del 60Co, si è scelto di collocare un unico rivelatore
al di sopra del campione e di cambiare la direzione di polarizzazione del 60Co,
applicando il campo magnetico esterno alternativamente nelle due direzioni (verso
l'alto e verso il basso).
scintillatore
e60Co

σ Co
e60Co

σ Co
17
L'esperimento termina nel momento in cui il sistema, per effetti termici, si depolarizza
(ciò avviene nell'arco di diversi minuti). A tale istante cessa infatti di esservi un asse
privilegiato (la direzione dello spin del 60Co) rispetto al quale misurare le distribuzioni
angolari.
Come verifichiamo che il sistema sia polarizzato? Il grado di polarizzazione del 60Co
viene trasmessa al 60Ni* nel decadimento e può essere tenuta sotto controllo verificando
l’anisotropia nell'emissione dei due fotoni emessi da parte del 60Ni*. Quando cessa
l’anisotropia nella emissione dei fotoni ciò significa che il 60Ni* si è depolarizzato e
l'esperimento è terminato.
I fotoni vengono rivelati da due scintillatori di NaI: la differenza tra i loro conteggi
fornisce una misura del grado di polarizzazione.
da questo momento in poi cessa
la polarizzazione del 60Co
18
Scriviamo l’andamento del numero di elettroni misurati all’angolo q (dove q è l'angolo
tra l'elettrone e la direzione di polarizzazione del 60Co) in funzione della variabile
 
pseudoscalare σ Co  pe (diviso per il numero di conteggi che avrei a quell'angolo quando
il sistema si è depolarizzato, cioè a caldo) nel modo seguente:




σ Co  p e cos θ
σ Co  p e
I( θ )
v
1α 
1α

1

α
cos θ

I(θ) a caldo
σ Co Ee
σ Co Ee
c
L’esperimento fornisce il valore di: a = - 1. Ciò significa che il numero di elettroni emessi
nello stesso emisfero dello spin del 60Co e quelli emessi nell'emisfero opposto hanno le
seguenti distribuzioni:
Iθ  1 
v
cos θ
c
N.B. Per 0  θ  90
 cos θ  0 (stesso emisfero)
Per 90  θ  180  cos θ  0 (emisfero opposto)
Iθ
90 θ  180
 Iθ
0 θ  90
La distribuzione angolare è quindi asimmetrica, cioè gli
elettroni sono emessi preferenzialmente lungo la
direzione opposta a quella dello spin del nucleo.
60Co

σ Co
19
Grafico dell'anisotropia dei due fotoni emessi dal
60Ni* nella sua diseccitazione. Finché il numero di
fotoni raccolti nel rivelatore di NaI posto a f = 90°
(equatore) e il numero di quelli raccolti nel
rivelatore posto a f = 0° (polo) sono diversi, ciò
significa che il 60Co è polarizzato. Se c'è un effetto
di violazione di parità, dobbiamo aspettarlo solo
finchè vediamo differenza.
Grafico dell'asimmetria tra il numero di elettroni
emessi nell' emisfero in cui è lo spin del 60Co e il
numero di quelli emessi nell' emisfero opposto.
Tale asimmetria è la dimostrazione della
violazione della parità da parte delle interazioni
deboli.
Fino a questo momento il
60Co
è polarizzato.
LE INTERAZIONI DEBOLI VIOLANO LA PARITÀ !!!
20
21
da Prof. Carlo Dionisi - Corso di Fisica Nucleare e
Subnucleare - Cap. 7:"Simmetrie e numeri quantici"
22
MISURA DELL’ELICITÀ DEL NEUTRINO
(1958, GOLDHABER, GRODZINS, SUNYAR)
Si studia la reazione di cattura di un elettrone da parte di un nucleo di Europio, che dà
luogo ad un nucleo eccitato di 152Sm* (S=1) che si diseccita per emissione di un fotone in
un 152Sm (S=0):
152
152
e +
Eu 
Sm* + ne
e- +
p 
n
= q.d.m.
= spin
eSz=1/2
L’elettrone è a riposo
152Sm*
 152Sm + 
+ ne
152Sm*
Sz=1
ne
Sz=-1/2
ne
hSm* = hn = -1
Sz=-1/2
152Sm*
hSm* = hn = +1
Sz=1
In ogni caso (anche se l’elettrone fosse ruotato dall’altra parte), l’elicità del 152Sm e del
neutrino sono uguali. Se quindi riesco a misurare qual è l’elicità del 152Sm*, ne posso
dedurre quella del neutrino. In generale quindi:
hSm* = hn
23
Se il fotone viene emesso con energia E > 960 KeV, esso è emesso nella stessa
direzione di volo del 152Sm*. In tal caso, il  mantiene la stessa elicità del 152Sm*.
h = hSm*
152Sm*
152Sm

(1)
h = hSm* = 1
Sz=1
(2)
152Sm*
Sz= -1
Sz=0
152Sm
Sz=0
Sz=1

h = hSm* = -1
Sz= -1
Per misurare l’elicità del fotone, gli si fa attraversare un ferromagnete con un campo
magnetico nel suo interno, disposto alternativamente in modo parallelo o antiparallelo alla
direzione dei fotoni. Se H è diretto nel verso del moto del fotone, gli elettroni del
ferromagnete saranno orientati come il campo, cioè nel verso di moto del fotone.
24
MISURA DELL’ELICITÀ DEL NEUTRINO (continua)
Se il fotone è del tipo (1) della pagina precedente (elicità positiva), non può essere
assorbito dagli elettroni disposti lungo un campo parallelo alla sua direzione di moto,
perchè l’elettrone non può saltare in uno stato di spin maggiore.
h = +1
NO
ASSORBIMENTO
H

e- (del ferromagnete)
Sz = +1/2
Sz=1
Esso può invece essere assorbito da elettroni disposti antiparallelalmente alla sua
direzione di moto, perchè in tal caso essi possono fare spin-flip, cioè possono invertire
l’orientazione del loro spin.

ASSORBIMENTO
Sz=1
H
e-
e-
Sz = -1/2
Sz = +1/2
25
MISURA DELL’ELICITÀ DEL NEUTRINO (continua)
Esattamente il contrario dovrà accadere se il fotone è invece di tipo (2), cioè a elicità
negativa (assorbimento per H parallelo alla direzione di volo del fotone e non assorbimento
per H antiparallelo). Ci si potrebbe aspettare di avere nel 50% dei casi una situazione come
quella della pagina precedente e nel 50% la situazione opposta. Invece, sorprendentemente,
il risultato sperimentale ottenuto è che il fotone è solo di tipo (2), cioè a elicità negativa,
cioè che viene assorbito da elettroni paralleli alla sua direzione del moto e non viene
assorbito da quelli antiparalleli.
h = -1

H
ASSORBIMENTO
Sz = +1/2
Sz=-1
NO
ASSORBIMENTO

Sz=-1
e-
eSz = -1/2
H
eSz = -1/2
26
Risultato: l’elicità del fotone emesso dal 152Sm* è negativa:
h = -1
ma l’elicità del fotone emesso dal 152Sm* era uguale a quella del 152Sm*:
h = hSm* = -1
e l’elicità del 152Sm* era uguale a quella del neutrino:
hSm* = hn = -1
CONCLUSIONE  IL NEUTRINO PUÒ AVERE SOLO ELICITÀ NEGATIVA
(e di conseguenza l'antineutrino solo positiva)
 MASSIMA VIOLAZIONE DELLA PARITÀ
( n e )L
p
P
(ne)R


( n e )R
p

-p
P
( n e )L
-p

P (ne)L = (ne)R
NON
ESISTE IN
NATURA!!
P ( n e )R = ( n e )L
NON
ESISTE IN
NATURA!!
27