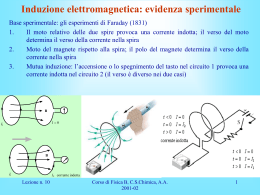
INDUZIONE MAGNETICA
B
A
N
S
A
I
Corrente elettrica I nel circuito:
Movimento circuito: FM sulle cariche
Movimento magnete: E nel filo
(relatività)
Stessi risultati con filo con corrente al
posto del magnete
Γ
B
I1
I2
Area S
+-
A
Variando I1 che genera B
I2 ind. nella spira
Si associa al moto cariche una f.e.m. indotta:
F
f .e.m.    dl   E  dl
q
 e

Integrale della componente tangente al
circuito delle forza per unità carica.
Legge di Faraday-Neumann -Lenz
d (B)
f .e.m.  dt
S
Significato del segno - (legge di Lenz):
flusso di B indotto compensa variazione
di flusso di campo B inducente
B(t)
I
B(t +t)
B’(t +t)
Legge di Lenz:determina il verso di
percorrenza della corrente indotta ,
quindi il verso della f.e.m. indotta
I tre modi per variare il flusso
1) Circuito con parte in movimento in B costante
l(t)
+
h
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
I
B = cost.
v
 S (B)  Bhl (t )
d S (B)
fem 
 Bh v
dt
(variazione di flusso tagliato)
Spiegazione fisica alternativa
l(t)
+
h
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
I
B = cost. ^
j
v
Questo caso si spiega con la forza di Lorentz
sulle cariche -e dell’elemento in moto:
F L   qe v  B ;
FL
 vB ;
 qe
FL // ^
j
FL
fem  
 dl  Bh v
q
Circuito e
Origine energia campo elettromotore?
l(t)
h
+
I
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
B = cost.
v
dΦS (B)
fem 
 Bh v  f
dt
R resistenza circuito
I  f /R
2
( Bh v)
Pelett.  VI  fI 
R
Forza su sbarra : F  IhB ˆi  B 2 h2 v/R ˆi
Per mantenere v = cost.
P  F  v  ( Bh v) / R  Pelett.
2
mecc
Sbarra in moto in presenza di B
^k
B
^i
+
^
B=Bk
FL
^j
v
^
v=vi
_
E
^
FL   q e ( v  B)  qe vB j
Spostamento (accumulo) carica fino:
FT   q e (E  v  B)  0
^
E  ( v  B)  vB j
FE   q eE  FL
Moto spira rigida in presenza di B
^k
^
B=Bk
^
v=vi
E
_ 2^
j
v
B
+
^i
+
_
E1
L
B uniforme 
E1 = E2
f.e.m   E  dl  E1L - E 2 L  0

d(B)
( Φ( B)  cos t 
0 )
dt
B non uniforme 
E1  E2
f.e.m   E  dl  0  corrente indotta
d(B)
( Φ( B)  cos t 
0 )
dt

2) Circuito fisso, B variabile
+ + +
+
+
+
+ + +
+
+
+
+ + +
+
+
+
+ + +
+
+
+
Area S
B = B(t)
FL =0
forza su cariche causata da?
Ipotesi di Faraday 
B
E  
t
d
S   E  nˆ dS   dt (S B  nˆ dS )
   E  n dS   E  dl
S
(Stokes)

d S (B)
B
f .e.m.   E  
dt
t
(variazione flusso concatenato)
3) Circuito rotante, B fisso
Generatore corrente alternata (a.c.)
A
ω
B
Area S
R
(t)
^
n
ΦS(B)  BSCos ( (t ))
B
 (t )  t
d S (B)
fem 
 BS  sin( t )
dt
fem BS 
I

sin( t )
R
R
Coefficiente mutua induzione
Γ
B
I1
I2
Area S
+-
A
Variando I1 che genera B
I2 ind. nella spira
F
f .e.m.    dl   E  dl
q
 e

Coefficiente mutua induzione
^
n1
dl2
I1
dl1
I2(t)
r
S1
12
S2
Γ2
Γ
1
d S 1 (B 2 )
f .e.m1 
dt
 S 1 (B 2 )   B 2  nˆ 1dS1  M 12 I 2
S1
d S 1 (B 2 )
dI 2
f .e.m1 
 M12
dt
dt
o dl1  dl 2
M 12   
 M 21
4 1 2 r12
(Henry)
Coefficiente mutua induzione solenoidi
Area
spire S1
Area
spire S2
 S 1 (B 2 )  M 12 I 2
o I 2 N 2
B 2   o I 2 n2 
l2
 o I 2 N 2 N1 S 2
 S 1 (B 2 )  B2 S 2 N1 
l2
 o N1 N 2 S 2
M 12 
l2
M21 = ??
M21 = M12
Coefficiente auto induzione solenoide
Area
spire S2
) 2 B( 2 S d
Id
L 
  2 mef
td
td
2
o I 2 N 2
B2 
l2
 S 2 (B 2 )  M 22 I 2  L I 2
2
S
2 2 N 2 I o
 2 S 2 N 2B  ) 2 B ( 2 S 
2l
2
S N o
L
2l
2
2
22
M
Trasformatore (ideale)
I1(t)

Vi(t)
N1
Vu(t)
N2

B1
materiale ferromagnetico
Nucleo materiale ferromagnetico
 non c’è flusso disperso
flusso attraverso ciascuna spira
dei due avvolgimenti è lo stesso
(come se due avvolgimenti sovrapposti)
Si dimostra che in questo caso :
Vu(t) M12 N2
=
=
Vi(t) M11 N1