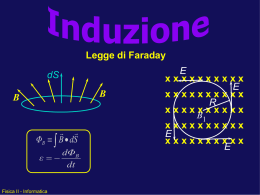
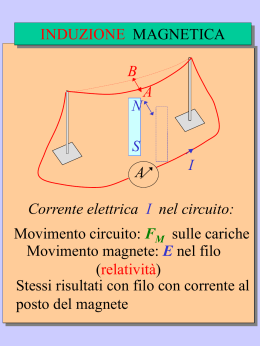
Induzione elettromagnetica: evidenza sperimentale
Base sperimentale: gli esperimenti di Faraday (1831)
1.
Il moto relativo delle due spire provoca una corrente indotta; il verso del moto
determina il verso della corrente nella spira
2.
Moto del magnete rispetto alla spira; il polo del magnete determina il verso della
corrente nella spira
3.
Mutua induzione: l’accensione o lo spegnimento del tasto nel circuito 1 provoca una
corrente indotta nel circuito 2 (il verso è diverso nei due casi)
B
I 0
I1
B
I1
I2 corrente indotta
Lezione n. 10
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
1
Legge di Faraday dell’induzione elettromagnetica
Faraday intuì che la corrente era indotta dalla variazione del flusso FB di B nel tempo.
Detta E la forza elettromotrice indotta nella spira (volt) e FB il flusso del campo
magnetico attraverso una superficie di cui la spira è contorno (weber), la legge di Faraday
è data da:
dF B
E=

dt
Si noti che il flusso FB può variare in seguito ad una variazione del campo magnetico, o
della forma della superficie attraverso cui si calcola FB.
Si parla quindi di flusso tagliato quando il circuito si muove o si deforma in una regione
delle spazio dove esiste B, oppure quando la sorgente di B si muove rispetto al circuito.
Si noti che il flusso concatenato con la spira varia anche quando il circuito sorgente di B
(primario) ed il circuito secondario sono fissi: se c’è una variazione di corrente nel
primario, questa provoca una variazione del campo magnetico B da essa generato cioè
una variazione di FB.
dF B
E=


l
E  dl

l
E  dl  
dt
E è una fem indotta (non localizzata) cioè il lavoro per unità di carica (volt) necessario
per portare una carica lungo un percorso chiuso. In questo caso tale energia è fornita da B
per cui in ogni regione dello spazio dove il campo magnetico B varia nel tempo è presente
un campo elettrico E non conservativo
Lezione n. 10
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
2
Legge di Lenz
Se la spira ha una resistenza R, l’intensità della corrente indotta vale:
E
i
R
vale a dire
B
1 dF B
i 
R dt
Se invece di una spira si ha una bobina di N spire, la f.e.m. indotta è:
dF B
E=
N
indotta nella spiradtha
I
La corrente
un verso tale che il campo
magnetico generato dalla corrente si oppone alla variazione di
campo magnetico che l’ha indotta (legge di Lenz).
Avvicinando un magnete ad una spira, B (e quindi FB) attraverso la spira
aumenta e viene indotta nella spira una corrente. La spira si comporta come un
dipolo magnetico m ed il verso della corrente è tale che m è orientato in senso
contrario a B. Se si allontana il magnete dalla spira, il verso di m cambia.
Analogamente succede muovendo la spira e tenendo fisso il magnete.
Lezione n. 10
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
3
Spira ruotante in un campo magnetico uniforme
Si consideri una spira di sezione A che ruoti con velocità
angolare costante w. Se il tutto è immerso in un campo
magnetico di intensità B uniforme, poiché la spira è in
rotazione, il flusso di B concatenato con la spira varierà
in continuazione, essendo dato da:
F B  A B cos  A B cosw t 
per cui vi sarà una f.e.m. indotta data da:
dF B
E=

 A B w sin w t 
dt
Se invece di una spira vi è una bobina con N spire, si
genera una f.e.m. alternata e quindi una corrente
alternata date da:
dF B
E=
 N
 N A B w sin w t 
dt
Lezione n. 10
E NABw
i 
sin w t 
R
R
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
4
La corrente alternata
i
Si è visto che una bobina con N spire ruotante con
velocità angolare costante w immersa in un campo
magnetico di intensità B uniforme genera una f.e.m.
indotta (ed una corrente indotta se inserita in un circuito)
esprimibili come:
E t   E0 sin w t 
E0  N A B w
E0
I
R
i t   I sin w t 
R
E(
V
E
 A
E0
La potenza erogata dal generatore vale:
t
pt   E i  E0 I sin 2 w t 
p
i
E0 I
I
t
t
Lezione n. 10
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
5
Trasferimenti energetici
Avvicinando un magnete ad una spira, per effetto della f.e.m. indotta
nasce anche una forza che si oppone al moto e che costringe a produrre
lavoro positivo contro quella forza. Tale energia si trasferisce nel
materiale sotto forma di energia termica (la spira si riscalda). Un
fenomeno analogo si verifica muovendo una spira immersa in un campo
magnetico. Nel caso in figura, una spira viene tirata verso destra a
velocità costante v fino ad uscire dalla regione in cui c’è B. Per far questo,
si deve compiere il lavoro dL = F dx poichè occorre applicare una forza
costante F, e quindi la potenza applicata vale P = F v.
D’altra parte, il flusso di B vale FB = B A = B L x e la sua variazione è:
E
Correnti di
Foucault
dF d
dx
 BLx   BL
 BLv
dt dt
dt
Per cui la spira è elettricamente equivalente al circuito in basso, e i = E / R.
Inoltre, sui tre lati della spira agisce la forza magnetica (BL) F1=iLB;
F2=F3= ixB con F2=-F3 e F4=0 perchè su quel lato B=0.
Sostituendo il valore di I si ottiene F=F1=B2L2v/R e
quindi la potenza applicata vale P=Fv=B2L2v2/R da
uguagliarsi con la potenza termica dissipata nella spira
P=Ri2=B2L2v2/R esattamente uguale alla precedente.
il lavoro necessario per estrarre la spira
attraverso B è convertito in energia termica dentro
la spira.
Lezione n. 10
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
6
Campi elettrici indotti
Se in un anello di Cu B uniforme aumenta in maniera uniforme (dB/dt=cost)  anche FB
aumenterà in maniera uniforme  nell’anello f.e.m. indotta  i indotta  all’interno
dell’anello c’è un campo elettrico indotto E le cui linee di forza sono circolari concentriche
con l’anello. Se B=cost allora E=0.
Una carica q0 in moto lungo la circonferenza di raggio r in un giro subirà il lavoro L=q0E
(E=f.e.m.) ma il lavoro può anche essere espresso come prodotto di forza per spostamento:
 F  ds  q E 2 r



cioè si ha
L  F  ds  q0 E  ds  E  E  ds
Ciò significa che il campo elettrico indotto NON è conservativo.
dF B
La legge di Faraday può essere scritta come:
E  ds  
dt
Il potenziale elettrico ha senso soltanto per le cariche statiche.
0

Lezione n. 10
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
7
Induttori ed induttanze
Induttore o induttanza: dispositivo utilizzabile per produrre un campo magnetico noto in
una determinata regione.
Il simbolo normalmente usato è:
(ricorda il solenoide)
Se la corrente circolante nelle N spire (o avvolgimenti) del solenoide in cui è presente un
flusso di B dato da FB è i, l’induttanza vale:
NF B
i
La grandezza NFB è chiamata flusso concatenato all’induttanza. L’unità di misura
L
dell’induttanza è l’henry. 1 H = 1 T m2 A-1.
Nel caso di un solenoide (indefinito) con n spire per unità di lunghezza percorso dalla
corrente i, si è visto che il campo magnetico vale B = m0 i n. Il flusso concatenato vale:
NFB  nl BA
NF
nlBA
nlm inA
B
0
e quindi l’induttanza è
L


 m 0 n 2lA
i
i
i
E vicino al centro del solenoide l’induttanza per unità di lunghezza vale L/l=m0n2A
Come nel caso della capacità, essa dipende da fattori geometrici, ed ha la generica
espressione di m0 = 4 10-7 T m A-1 (o H/m) moltiplicato per una lunghezza.
Lezione n. 10
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
8
Autoinduzione
Se due bobine (induttanze) sono molto vicine l’una all’altra, una
corrente variabile nella prima creerà una f.e.m. indotta nella
seconda. Per lo stesso motivo, una f.e.m. indotta apparirà anche
nella prima bobina (fenomeno dell’autoinduzione).
Se in una bobina varia i, in essa si genera una f.e.m.
autoindotta EL.
Il verso è tale per cui la f.e.m. autoindotta EL ende ad opporsi al
cambiamento che la causa:
NF B  Li
d  NF B 
di
EL  
 L
dt
dt
È possibile definire una d.d.p. autoindotta ai capi di un’induttanza
VL= EL. In un’induttanza reale occorre considerare, oltre a L, anche
la resistenza interna del filo dell’induttanza r.
Lezione n. 10
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
9
Circuiti RL
Si consideri un circuito ad una maglia con R e L ed un generatore E. Quando il tasto S
chiude il circuito, in assenza di L la corrente tenderebbe istantaneamente al valore i0= E /R.
La presenza di L invece causa l’insorgere della f.e.m. indotta EL che limita la crescita di i.
Applicando la legge delle maglie di Kirchhoff al circuito RL, si ha:
 iR  L
di
E  0
dt
Integrando tale equazione ed imponendo le condizioni iniziali i=0 per t=0 e i= i0= E /R per
t, si arriva all’espressione:
 t
E
i  1  e
R
tL



dove tL=L/R è la costante di tempo
induttiva. Per t=tL la corrente vale
i = 0.63 i0.
Spegnendo in queste condizioni il
generatore, invece, si ha:
di
iR  L  0
dt
Lezione n. 10
E  tt L
i e
R
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
10
Energia in un campo magnetico
L’equazione delle maglie di Kirchhoff applicata ad un circuito RL con generatore E è:
 iR  L
di
E  0
dt
e moltiplicando per i si ottiene:
di
Ei  i R  Li  0
dt
2
Tali termini hanno le dimensioni di una potenza. Il primo rappresenta la potenza erogata
dal generatore, il secondo la potenza dissipata nella resistenza per effetto Joule ed il terzo
la potenza immagazzinata nel campo magnetico. L’integrale di tale termine fornirà
l’energia magnetica EL:
t
i
EL   Li
0
di
1
dt   Lidi  Li 2
dt
2
0
Nel caso di un tratto l di un solenoide indefinito di sezione A con n spire per unità di
lunghezza, la densità volumica di energia magnetica vale:
EL Li 2 1
1 2
2 2
uL 

 m0n i 
B
Al 2 Al 2
2m 0
Come nel caso della densità volumica di energia elettrica,
tale risultato è stato ottenuto per il solenoide ma ha validità
generale.
Lezione n. 10
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
11
Mutua induzione
La corrente i1 circolante nella bobina 1 prodotta da una batteria produce il campo B1. La
seconda bobina, senza batteria, è attraversata dal flusso di B1 F21. Si definisce mutua
induttanza della bobina 2 rispetto alla bobina 1 la grandezza:
NF
di
dF 21
M 21  2 21 Se i1 varia nel tempo, si ha M 21 1  N 2
e per la legge di Faraday:
i1
dt
dt
E 2   M 21
di1
dt
è la f.e.m. indotta nella seconda bobina.
Se invece è la bobina 2 ad avere il generatore
di f.e.m. variabile, la corrente i2 circolante
nella bobina 2 produce il campo B2 e la
prima bobina, senza batteria, è attraversata
dal flusso di B2 F12. Si ha:
di2
dt
Le costanti di proporzionalità M12 e M21
coincidono per cui si ha:
M = M12 = M21
M si misura in henry come L.
E1   M 12
Lezione n. 10
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
12
Induttanze in serie ed in parallelo
Induttori in serie
(senza accoppiamento magnetico)
Induttori in parallelo
(senza accoppiamento magnetico)
i
L1
E
L3
L2
Per la legge di Kirchhoff delle maglie, le
f.e.m. si sommano:
di
di
di
di
 L1  L2  L3  L
dt
dt
dt
dt
L
L
i
i
Lezione n. 10

Da cui si ottiene:
Cioè:
L3
L2
Per la legge di Kirchhoff dei nodi, le
correnti si sommano:
i  i1  i2  i3  di  di1  di2  di3
dt dt dt dt
Per la legge di Faraday:
L  L1  L2  L3
Per cui si ha:
L1
Cioè:
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
E
E E E
 

L
L1 L2 L3
1 1
1
1



=
L L1 L2 L3
1

L

i
1
Li
13