PARABOLA E
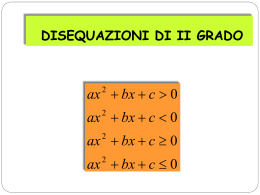
DISEQUAZIONI DI 2° GRADO
Mappa dell’Unità Didattica
OBIETTIVI TRASVERSALI
PREREQUISITI
TEMPI
OBIETTIVI SPECIFICI
parabola e
disequazioni di
II grado
STRUMENTI
METODOLOGIA
CONTENUTI
VERIFICHE
inizio
Prerequisiti
• Operazioni sugli insiemi
• Equazioni di I e II grado
• Disequazioni razionali intere di I grado
• Concetto di funzione
• Rappresentazione grafica di una funzione
• Concetto di intervallo
• Traslazione
• Uso del Derive
mappa
Obiettivi trasversali
• Saper utilizzare un’adeguata terminologia
• Saper estendere le conoscenze acquisite adattandole
alle diverse situazioni
• Saper utilizzare il computer in ambiente Windows
• Saper risolvere problemi
mappa
Obiettivi specifici
• Saper studiare il segno di una funzione di II grado in
una variabile
• Acquisire tecniche per la risoluzione algebrica e grafica
di disequazioni di II grado in una variabile
• Acquisire la capacità di tradurre problemi di II grado in
forma algebrica
mappa
Contenuti
• Funzione quadratica
• Parabola
• Disequazioni razionali intere di II grado
mappa
Metodologia
Gli argomenti saranno proposti scegliendo un percorso
didattico finalizzato a stimolare l’interesse, la curiosità e
la riflessione degli studenti anche mediante l’uso di
mezzi informatici.
Alla lezione di tipo frontale si accosteranno discussioni
guidate, lavori individuali, di gruppo ed esercitazioni
pratiche.
L’impostazione della lezione sarà di tipo interattivo allo
scopo di personalizzare il percorso di apprendimento in
base alle capacità di ogni singolo allievo, mediante
schede di approfondimento e di recupero in itinere. mappa
Strumenti
• Lavagna
• Libro di testo
• Appunti
• Computer
• Lavagna luminosa
mappa
Verifiche
• Schede di controllo dei prerequisiti
• Verifiche scritte
• Verifiche orali
Parametri di valutazione
mappa
Tempi
Accertamento prerequisiti 1 ora
Parabola:
lezione frontale ed esercitazione con Derive 2 ore
correzione e discussione degli esercizi svolti
dagli studenti 1 ora
attività di recupero e potenziamento 1 ora
Disequazioni:
lezione frontale ed esercitazione con Derive 2 ore
correzione e discussione degli esercizi svolti
dagli studenti 1 ora
attività di recupero e potenziamento 1 ora
verifica finale 2 ore
mappa
Parametri di valutazione del test finale
Tale valutazione costituisce il momento conclusivo dell’U.D. ed attesta i miglioramenti
conseguiti dal singolo allievo, dall’intera classe e la validità della progettazione
effettuata.
Si valutano i seguenti tre fattori: conoscenze, competenze, capacità; per ognuno di essi
si danno cinque indicatori.
Autonoma
Sicura
Accettabile
Incerta
Capacità
Inesistente
Puntuale
Aderente
Adeguata
Approssimata
Competenza
Marginale
Rigorosa
Approfondita
Sufficiente
Limitata
Scarsa
Conoscenza
Scheda di controllo dei prerequisiti
Risolvere in R le seguenti equazioni
2x  5  0
4 x 2  5x  1  0
Risolvere la seguente disequazione interpretando
geometricamente l’insieme S delle soluzioni
x 1 2x 1 x 1 x 2x 1


 
2
3
6
2
3
Risolvere il seguente sistema di disequazioni

1

x

1

2
x


  x  21  x 

2



 x  12  21  x    x  2 2  3 x


Tracciare il grafico della funzione y=3x+4
mappa
La curva di equazione y =
2
ax
Tracciamo il grafico della curva associata all’equazione
di II grado y = x2
Essa è simmetrica rispetto
all’asse delle ordinate,
y
cioè f(x)=f(-x)
per cui per costruire il
grafico basta determinare
alcuni suoi punti di ascissa
positiva
x
Consideriamo ora alcune curve del tipo y = ax2 con a>0
y = x2
y = 2x2
y = 3x2
Esaminando le curve possiamo trarre alcune
conclusioni
 ognuna ha come asse di simmetria l’asse y
 tutte passano per l’origine degli assi,
che è il punto di ordinata minore
 tutte volgono la concavità verso l’alto, hanno
la stessa forma e l’apertura diminuisce
all’aumentare di a
Consideriamo ora le stesse curve con a < 0
y = -x2
y = -2x2
y = -3x2
I grafici risultano simmetrici dei precedenti
rispetto all’asse delle x
y=ax2 come luogo geometrico
Possiamo definire la curva come luogo geometrico dei
punti del piano equidistanti da un punto fisso F (detto
fuoco) e da una retta detta direttrice.
y
PF  PH
 P(x;y)
F(0;p)

x
H
y=-p
PF  x   y  p  



PH  y  p

2
2
x   y  p  y  p
2
2
1 2
2
sviluppando e riducendo si ottiene: y 
x  ax
4p
a
V(0;0)
F(0; 1/4a)
direttrice y= -1/4a
asse x=0
Riassumendo:
una funzione del tipo y = ax2 con aR - {0} ha come
diagramma una curva che chiamiamo parabola, la
quale ha:
 vertice nell’origine degli assi del sistema di
riferimento,
 asse di simmetria coincidente con l’asse
delle ordinate,
 concavità rivolta verso l’alto se a>0, verso
il basso se a<0
Vogliamo ora determinare l’equazione di una parabola
con asse di simmetria parallelo all’asse delle y e vertice
nel punto V(xo,yo).
Consideriamo una parabola del tipo y = ax2 e la
sottoponiamo ad una traslazione del vettore
t ( xo ; yo )
2
2









y ax
y
y
a
(
x
x
)
o
o
 
eq. di go
 x x xo 




y
y
y

o 
eq. di g
Come si vede l’equazione di una parabola con asse di
simmetria parallelo all’asse y e vertice in V(xo;yo) è
y - yo = a (x - xo)2
y = a x2 - 2 a xo x + a xo2 + yo
b
si ottiene:
y = ax2 + bx + c
c
b
Dalla -2axo = b ricaviamo che xo  
2a
e quindi, essendo yo = f(xo), si ottiene
 b 2  4ac

yo 

4a
4a
Concludendo la parabola di equazione y = ax2 + bx + c
ha per vertice il punto
b



V    ; 
 2a 4a 
parabola di equazione
y = ax2 + bx + c
y = -3x2 + 5x +2
y = 4x2
y = 2x2 - 4x
y = -x2 - 2x - 1
y = 2x2 + 3
y
4 2 8
x  x3
25
5
1
y   x2  2x  3
2
 = b2 - 4ac
52-4(-3)2=49
=49
asse di
simmetria
x
b
2a
5
2 3
5
x
6
x
vertice

 b
V   , 
 2a 4a 
 5 49 
V , 
 6 12 
fuoco
direttrice
 b 1  
F ,

 2a 4a 
1  
y
4a
yF=…..=4
5 
F  ,4 
6 
 1  49
4 3
25
y
6
y
intersezioni
con l’asse x
intersezioni
con l’asse y
-3x2 + 5x +2=0
x = 0;
1
x , x2
3
y=2
Esercizi applicativi del concetto di parabola
Una ditta intende creare su di un suolo di sua proprietà un’area di parcheggio
rettangolare per le automobili dei suoi dipendenti. Nei suoi magazzini sono disponibili
soltanto 100 metri di recinzione metallica. Quali devono essere le dimensioni del
parcheggio affinché si realizzi la massima capienza possibile?
Un ricco signore ha decretato che alla sua morte i suoi beni, che ammontano ad otto
miliardi di lire, debbano essere divisi tra l’unico nipote ed un’associazione benefica. Egli
è però una persona che ama i giochi matematici; inoltre non ha molta fiducia nelle
capacità di gestire denaro del nipote. Stabilisce quindi che le cifre che i due eredi
avranno dovranno essere tali da rendere minima la somma tra il quadrato della parte
destinata al nipote ed il doppio di quella destinata all’associazione. Sarà contento il
nipote della decisione dello zio?
Rappresentare in un opportuno sistema di riferimento cartesiano le parabole aventi
equazione assegnata:
y=-x2+2x
y =x2-7x+12
Le disequazioni di II grado
Una disequazione intera di II grado può sempre essere
riportata alla forma ax2 + bx + c > 0
 y  ax  bx  c
che a sua volta può essere scritta come 
y0

2
l’interpretazione grafica di tale sistema è la seguente:
determinare i punti della parabola aventi ordinata positiva
Se la disequazione da risolvere è del tipo ax2 + bx + c < 0
si considera invece il sistema
2
 y  ax  bx  c

y0

e perciò si dovrà determinare l’insieme dei punti
della parabola con ordinata negativa
se nella disequazione compare il segno  o  si dovranno
considerare come soluzione anche gli eventuali punti di
intersezione della parabola con l’asse delle x
questi si ottengono risolvendo l’equazione ax2 + bx + c = 0
 b  b  4ac

2a
2
x1/ 2
esempio 1
Risolvere la disequazione x2 - 4  0
y  x  4
Tale disequazione equivale al sistema 
 y0
2
Dobbiamo perciò determinare i punti della parabola y = x2 - 4
che giacciono nel semipiano delle ordinate negative o nulle
Tale parabola ha la concavità rivolta verso l’alto ed
interseca l’asse delle x nei punti A(-2;0) e B(2;0)
y
•A
-2
B•
2


S:[-2;2]
x
esempio 2
Risolvere la disequazione - x2 + 5x + 6 < 0
 y   x  5x  6
Tale disequazione equivale al sistema 
y0

2
Risolviamo la - x2 + 5x + 6 = 0  x =
-1
6
S:]-;-1[]6;[
esempio 3
 y  x2  6x  9

y0

x2 + 6 x +9  0
x2 + 6 x + 9 = 0  x1 = x2 = -3
S = {-3}

esempio 4
3 x2 - x + 1 > 0
 y  3x 2  x  1

y0

3x2 - x + 1 = 0   < 0  non ha radici reali
S=
esempio 5
- x2 + 2 x - 1 > 0
 y  x2  2x 1

y0

- x2 + 2 x - 1 = 0  x1 = x2 = 1
S = {Ø}
esempio 6
- x2 + 8 x - 17  0
 y   x 2  8 x  17

y0

-x2 + 8 x - 17 = 0   < 0  non ha radici reali
S=
=b2-4ac
parabola
>0
(x1 < x2)
x1
x2
valori di x che soddisfano la disequazione
ax2+bx+c>0
ax2+bx+c0
x < x1
x  x1


x > x2
x  x2
qualsiasi
a>0
=0
x1= x2
<0
x con
b
x
2a
x
ax2+bx+c<0
ax2+bx+c0
x1<x<x2 x1 x x2
x
nessun
valore
di x
b
x
2a
x
nessun
valore
di x
nessun
valore
di x
Dall’analisi dello schema si deduce che:
>0
ax2 + bx + c assume lo stesso segno di a per
valori esterni all’intervallo delle radici
=0
ax2 + bx + c assume sempre lo stesso segno
di a escluso i valori per i quali si annulla
<0
ax2 + bx + c assume sempre lo stesso segno di a
trinomio
ax2 + bx +c
-2x2+x+3
2x2+x+1
-x2-2x –1
6x2 + x –2
-x2 +2x – 3
-3x2 +x -2
scrivi
l’equazione
della parabola
corrispondente
y = ax2 + bx +c
y = -2x2+x+3
y= 2x2+x+1
scrivi il
coefficiente del
termine di 2°
grado e indica il
tipo di concavità
della parabola
a =-2
La parabola
volge la
concavità verso
il basso
determina le
intersezioni della
parabola con l’asse
delle x
a=2
La parabola
volge la
concavità verso
l’alto
2x2+x+1 = 0
non ci sono
intersezioni
disegna il grafico
approssimato della
parabola
Scrivi i valori di
x per cui
ax2 + bx +c > 0
Scrivi i valori di
x per cui
ax2 + bx +c < 0
-1 < x < 3/2
x < -1 V x > 3/2
R

-2x2+x+3 = 0
x1 =-1, x2=3/2
disequazione
scrivi
l’equazione
della parabola
corrispondente
al trinomio a
primo membro
scrivi il coefficiente
del termine di 2°
grado e indica il tipo
di concavità della
parabola
a=9>0
La parabola volge la
2
9x2 + 6x + 1  0 y = 9x + 6x +1
concavità verso
l’alto
-2x2 + 3x + 2 >0
9x2+ 6x + 2  0
6x2 -11x + 3  0
-16x2 + 8x –1<0
-5x2 + 2x – 1 <0
9x2 -12x + 4 < 0
determina le
intersezioni della
parabola con l’asse
delle x
9x2 + 6x +1 = 0
x1 = x2=-1/3
disegna il grafico
approssimato della
parabola
Scrivi i valori di x
che verificano la
disequazione
x = -1/3
Esercizi applicativi delle disequazioni di II grado
Risolvere per via algebrica e ricorrendo al grafico della parabola le seguenti disequazioni:
-6x2+7x-20
x2-6x+8>0
4x2+12x+9<0
-x2-6x-9>0
2x2-3x+50
2x2+x+10
Si determini il lato di un quadrato affinché la sua area diminuita di 3 sia maggiore di 6.
Una ditta ha una capacità produttiva massima mensile di kg 1500 di una merce. Per la
produzione sostiene una spesa fissa mensile di lire 500000 ed un costo di lire 1000 per
ogni kg prodotto. La domanda della merce è espressa in funzione del prezzo dalla
relazione x=2400-0,4p dove x è la quantità di merce e p è il prezzo al kg. Calcolare la
quantità di merce che si deve produrre per ottenere il massimo utile, nell’ipotesi che tutta
la quantità prodotta sia venduta.
Verifica sommativa finale
La prova è composta da domande di tipo vero - falso,
quesiti a risposta multipla, frasi da completare ed esercizi da
risolvere.
Punteggio massimo = 10
Durata della prova: 2 ore
Quesiti vero - falso (0,2 punti per ogni risposta esatta)
Indica quali affermazioni sono vere (V) e quali false (F)
a) La disequazione x2 + x +1 > 0 non ammette soluzione
V
F
V
F
c) La disequazione ax2 + c > 0 non ha soluzione se a >0 e c > 0
V
F
d) La disequazione ax2 + c > 0 non ha soluzione se a >0 e c < 0
V
F
e) Se  > 0 la disequazione ax2 + bx + c > 0 ha sempre infinite soluzioni
V
F
f) Il numero zero non appartiene mai all’insieme soluzione della disequazione ax 2 + bx < 0
V
F
g) Il numero zero appartiene sempre all’insieme soluzione della disequazione ax 2 + c > 0
V
F
h) La disequazione -x2 -1  0 non ammette soluzione
V
F
i) La disequazione x2 + x + 2 >0 è verificata x
V
F
l) La disequazione x2 -x + 3  0 non ammette soluzione
V
F
m) La disequazione x2 -x + 1 > 0 è verificata x
V
F
n) La disequazione x2 + 10 < 0 non ammette soluzione
V
F
b) Una disequazione di 2° grado ax2 + bx + c >0 e con il vertice della parabola
corrispondente nel 2° quadrante, non è verificata da alcun valore di x
Quesiti a risposta multipla (0,5 punti per ogni risposta esatta)
a) La seguente figura illustra la risoluzione grafica di una disequazione di 2° grado. A quale disequazione, fra le
seguenti, si riferisce?
•
x2 - 3x + 2 < 0
•
- x2 - 3x + 2 < 0
•
- x2 - 3x + 2 > 0
•
x2 - 3x + 2 > 0
b) La parabola di equazione y = (k+1)x2 +(k-1)x -2k, k, passa per il punto P(-2,6)
•
per nessun valore di k
•
per k = - 
•
x
•
per k = -1
c) La disequazione x2 + ax > 0, con a >0, è verificata per:
•
x < 0 v x > -a
•
-a < x < 0
•
x < -a v x > 0
•
0 < x < -a
Esercizi di completamento
Completare le seguenti frasi: (0,1 punti per ogni risposta esatta)
a) La parabola è il ……….. dei punti del piano …………………. da un punto fisso detto ………… e da una retta
fissa detta ………………
b) L’equazione y=ax2 rappresenta una parabola avente come ……….. l’asse y, come vertice il punto di coordinate
(..…;……), come fuoco il punto F(..…;……) e come direttrice la retta y = …….
c) Data la parabola y = ax2 + bx + c, se a > 0 la parabola ha concavità verso ………..
Completare: (0,4 punti per ogni risposta esatta)
a) x
è soluzione di
x2 ……. 25 > 0
b) impossibile
è soluzione di
x2 ……... 7 < 0
c) 2 < x < 5
è soluzione di
x2 - … x + … < 0
d) x
è soluzione di
2x2 - x + 1 ... 0
e) x  4 V x  6
è soluzione di
x2 - … x …..  0
Esercizi da risolvere (max 1 punto per ogni esercizio)
a) Descrivi, senza disegnarla, la parabola individuata dall’equazione y = x2+6x+5, precisando:
1) se è concava verso l’alto o verso il basso;
2) se incontra l’asse x e, in caso affermativo, in quanti punti;
3) se presenta punti di ordinata positiva;
4) se presenta punti di ordinata negativa.
b) Data la disequazione 4x2 - 12x +9 > 0
• risolverla algebricamente
• risolverla graficamente
c) Determinare i valori del parametro k per i quali la seguente equazione di secondo grado ammette soluzioni reali.
4x2 - 4kx + 4k2 - 3 = 0
Attività di recupero e potenziamento
In una fase successiva saranno proposti esercizi di recupero o potenziamento in
base alle capacità dei singoli allievi.