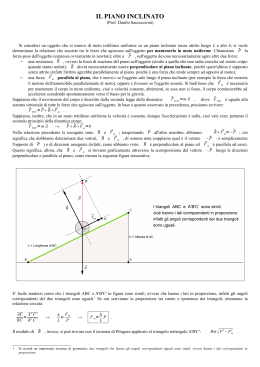
ROTOLARE
giù per un piano inclinato
Corpo rotondo omogeneo di raggio R che
rotola senza strisciare su un piano inclinato
di  sull’orizzontale in direzione x
ESEMPIO 1
Rotolare giù per una discesa
Corpo rotondo omogeneo di massa M e raggio R che
rotola senza strisciare per un piano inclinato di 
sull’orizzontale. Trovare la componente x
dell’accelerazione del CM, dovuta alla gravità

Poniamo l’asse x sul piano inclinato.
s
Diagramma delle forze che agiscono sul corpo:
Fg è la forza gravitazionale ed è diretta verso il
basso. La coda del vettore è applicata nel CM.
Osserviamo sulla figura le componenti normale e
tangenziale al piano inclinato.
N è la forza normale che agisce nel punto P, ma è
stata traslata lungo la sua direzione,ed applicata al
CM
Fgsin è la componente tangenziale ed è diretta
verso sinistra. La palla rotola verso sinistra
fs è la forza di attrito, che giace sul piano inclinato;
si oppone al moto del corpo, e quindi è diretta verso
destra
la forza di
attrito fs
genera un
momento
meccanico
che tende
a far
ruotare il
corpo

s
Rotolare giù per una discesa:cont.
Equazione del moto di
traslazione del CM
f s  Mg sin   Macm
Equazione del moto di
rotazione attorno al CM,
dovuta alla fs
 s  Rf s  I cm
Il corpo rotola senza
strisciare,quindi il moto è
volvente
sostituendo
=-a/R
acm=-R
f s   I cm
acm
2
R
Sostituendo fs , nella equazione del moto di traslazione del CM.
 I cm
acm
 Mg sin   Macm
2
R
acm
g sin 

2
1  I cm / MR

