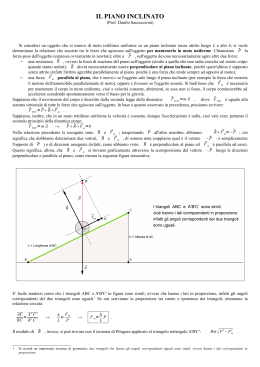
Esempio 1
Un blocco di massa m = 10kg deve essere trasportato dalla base all’estremità superiore
di un piano inclinato, percorrendo 5 m sul piano inclinato, e sollevandosi ad una quota
di 3 m. Supponendo il piano inclinato senza attrito, quale lavoro compie una forza F,
parallela al piano inclinato, che spinge il blocco a velocità costante ?
Come prima cosa, inquadriamo graficamente il problema indicando i dati noti
5m
3m
θ
F
Le forze che agiscono sul blocco sono indicate nel diagramma di seguito. Poiché il problema
parla di moto a velocità costante lungo il piano inclinato, la risultante delle forze lungo x deve
essere = 0, cioè
Da cui
F – mg sin (θ) = 0
[ notiamo che sin (θ) = 3/5 ]
F = mg sin(θ) =
= 3/5 x 10kg x 9,8 m/s2 = 58,8 nt
N
L = F • d = F d cos(0°) = 58,8 nt x 5 m =
F
= 294 Joule
mg
5m
3m
θ
F
Esempio 2
Supponiamo di tirare una slitta di peso P = 10kg per 10 m su di una superficie orizzontale a
velocità costante. Supponiamo che il coefficiente di attrito dinamico sia
μc =
0,20
e che la forza applicata per trascinare la slitta formi un angolo di 45° con l’orizzontale.
Quesito: quale lavoro compiamo sulla slitta ?
Come prima cosa, inquadriamo graficamente il problema indicando i dati noti.
10 m
10 kg
μc = fc / N = 0,2
45°

Notate la definizione di coefficiente d’attrito
Le forze che agiscono sulla slitta sono indicate nel diagramma di seguito.
Il lavoro L fatto nel trascinare la slitta è dato da:
y
L = F • d = F d cos (θ)
N
Per calcolare F ci riferiamo al diagramma delle forze. Poiché
il moto orizzontale avviene a velocità costante, la
risultante delle forze agenti lungo l’asse x deve essere = 0
F
θ=45°
x
fc
F cos (θ) + fc = 0  F cos (θ) = -fc
P
dove:
fc = μc N
Non essendoci moto lungo l’asse y, anche la risultante delle
forze agenti lungo l’asse y deve essere = 0
F sin (θ) + N – P
=0
Le due equazioni sono quindi:
F cos (θ) − μc N = 0
F sin (θ) + N – P = 0
I dati noti sono:
μc = 0,2
P = 10 kg
θ = 45°
Le incognite sono:
F
N
Da cui risulta:
N = F cos (θ) / μc
F sin (θ) + F cos (θ) / μc – P = 0
F (sin(θ) + cos(θ)/ μc ) = P  F = P / (sin(θ) + cos(θ)/ μc )
Per comodità riscriviamo così la formula ricavata per F:
F = P / (sin(θ) + cos(θ)/ μc )  F = μc P / (μc sin(θ) + cos(θ) )
Adottando i valori noti:
μc = 0,2
P = 10 kg
θ = 45°
Si ha:
F = 0,2 x 10kg x 9,8 m/s2 / (0,141 + 0,707) = 23,5 nt
Quindi il lavoro fatto su
d = 10m è:
L = F d cos(θ) = 23,5 nt x 10 m x 0,707 = 166 joule