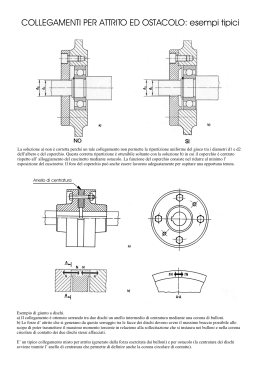
Dischi e cilindri assialsimmetrici
Accoppiamenti forzati – Dischi e cilindri
Corpi assialsimmetrici elastici
relazioni di base
y
z  0
Se R>>h Stato piano di tensione   z  0
Se R<<h
r
O
h


x
Stato piano di deformazione
z
R
Ipotesi di base per i dischi
Stato piano di tensione   z  0
 r 
E
Elasticità isotropa    
2

1


 
1    r 
 1   

  
EQUILIBRIO DELL’ELEMENTO INFINITESIMO
r 
d
r
r+dr

F
r

d
r
( r  d r )( r  dr ) ddz   r rddz  2  drdz sin(
cioè
r
d r
  r     Fr  0
dr
d
)  Frddrdz  0
2
DEFORMAZIONI E SPOSTAMENTI
r+dr
u+
du
u
r
d
dr'
dr 'dr dr  du  dr du
r 


dr
dr
dr
(r  u )d  rd u
 

rd
r
Sistema di equazioni
d r
  r     Fr  0
dr
du
r 
dr
u
 
r
   r 
 r 
1
E





1
1  2 

   
  
r
Da questo sistema si può ottenere un’unica equazione:
E
d 2u du u
(r

 )  Fr  0
1  2 dr 2 dr r
ovvero
E d 1 d

(
ur
)
  F  0
1  2 dr  r dr
Dischi con F=0
Caso della pressione interna
Integrando l’eq. differenziale con F = 0 si ha:
u  C1
a
p
b
r C2

2 r
Le due costanti si ottengono
imponendo le due condizioni al contorno
 r (a)   p
 r (b)  0
La soluzione completa risulta:

k 
b2 
u
(1  )r  (1   )

b2
k (1  2 )
E
r 
a
2
b
 r  k (1  2 )
r
b2
   k (1  2 )
r

pa 2
k 2 2
b a
2k
a
p
b
r
r
Dischi con F=0
Caso della pressione esterna
•
Questo caso si tratta in modo analogo
al precedente, ottenendo gli stessi
risultati dove però si sostituisca a
con b
p
a
b
pb 2
k' 2
a  b2
k' 
a2 
u  (1  ) r  (1   ) 
E
r 

a
b
r
2
a
 r  k ' (1  2 )
r
a2
   k ' (1  2 )
r
r
2
2 pb
a2  b2

p
Disco pieno con pressione esterna
p
R
1 
u   pr
E
 r     p
Disco rotante scarico ai bordi
F   2 r
C1r C2  2 (1  2 )r 3
u  uo  u p 
 
2 r
8E
Condizioni al contorno:
b
a
 r (a)   r (b)  0
La soluzione

k" 
 2 (3  )
8

 
b2a 2
2
2
u
 (1  2 )r 3 
(3  )(1  )(b  a )r  (3  )(1  )
8E 
r

2 2
ba
 r  k " (b 2  a 2  2  r 2 )
r
b2a 2
1  3
2
2
   k " (b  a  2  r 2
)
r
3 
2
Disco rotante scarico ai bordi

 2

(3  )b2  (1  )a 2 
4
 2

(3  )a 2  (1  )b2 
4

r
a
b
ab
 2 (3  )
(b  a)2
8
r
Disco pieno rotante di raggio a
k'
 2
8
1 
u  k'
[(3   ) a 2 r  (1   ) r 3 ]
E


r2
1 2


 r 


2
a

k
'
a
(
3


)
 

2 
  
1  1  3 r 

3  a 2 


Disco con effetti termoelastici F = 0
•
La distribuzione di temperatura assialsimmetrica lungo il raggio
costituisce un “carico termico”, rappresentato dalla deformazione
εT(r)=αΔT(r).
T  T
a
b
•
L’eq. differenziale dei dischi diviene:
d 1 d
d T

(
ur
)

(
1


)
0

dr  r dr
dr
Integrando si ha:
Cr C
1 
u 1  2 
2
r
r
r
 r
a
T
dr
Disco con effetti termoelastici
Con le condizioni  r (a)   r (b)  0
Si ottiene
 C1 
1
  2
2
C2  b  a
b
 r
a
T
 2(1  ) 
dr  2

a (1   )
b
u
 r
E

 
E
N .B  se
 T  cos t
allora   r     0
u  T r
 r
T
dr
a
b2  a 2
[(1  )r  (1  )


1
 2
2
 b a

a2
1 
]
r
r
 a 
1 2  1



a r T dr  ar 2   r 2
1 

2 

r 

r
 r
T
dr
a
2
b
 1  0 
r

dr
 

T
a
 1    T 
r
Accoppiamento forzato
mozzo-albero
Per trasmettere una coppia
L
Congruenza all’interfaccia
C
d1
d2
p
p
C
d1m
 um
2
d1a
 ua
2
d1m
d
 um  1a  ua
2
2
quindi
i  d1a  d1m  2(um  ua )