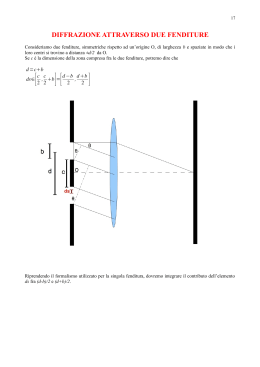
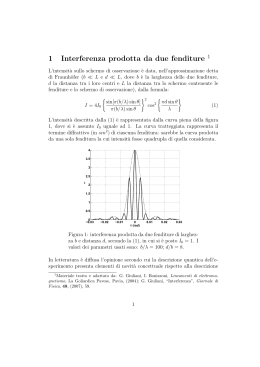
Liceo Scientifico “G.Marinelli”
Classe 4^ H
A.S. 2003/2004
INTERFERENZA
LASER
L’esperimento delle due fenditure con i
sensori online
A cura di:
Emanuel Castellarin, Pierangelo Degano, Laura Passaponti
OBIETTIVO
Studiare il fenomeno dell'interferenza
confrontando i risultati del modello
teorico con le misure registrate con i
sensori on-line.
I RISULTATI:
1-Sono sovrapponibili?
2-Per quali motivi si differenziano?
MATERIALI
Un puntatore laser
Le due fenditure
Un calcolatore con interfaccia
Un sensore di intensità luminosa collegato all’interfaccia
Un sensore di posizione angolare con traslatore lineare
MODO DI OPERARE
CONDIZIONI:
 Ambiente buio
 Allineamento accurato tra fenditure e
schermo
SI REGISTRA:
La distribuzione angolare dell’intensità luminosa
sullo schermo
IL TRAGITTO DELLA LUCE:

PUNTATORE
LASER
DOPPIA
FENDITURA
SCHERMO
E SENSORE
INTERFACCIA
E PC
L’IMMAGINE OSSERVATA
SULLO SCHERMO
OSSERVIAMO SULLO
SCHERMO
La luce che raggiunge lo schermo forma
frange chiare e frange scure.
La distanza tra ciascun massimo e
minimo è costante.
L’intensità dei massimi non è costante.
Le misure
Abbiamo anche misurato con un sensore la
distribuzione angolare dell’intensità sullo schermo
FARE PREVISIONI PER
INTERPRETARE
L’ipotesi teorica prevede che, per il principio di
sovrapposizione, sullo schermo compaiano frange
chiare intervallate da frange scure.
La distanza tra un massimo ed un minimo deve
essere costante
Il grafico dell'intensità in funzione della posizione
deve apparire con l’andamento di una sinusoide.
IL MODELLO MATEMATICO
IMPLEMENTATO IN EXCEL
Per studiare il fenomeno in Excel abbiamo
usato la formula:
k

I  4 A cos   x1  x2  
2

2
2
partendo dal principio di sovrapposizione.
ECCO COME ABBIAMO PROCEDUTO:
X
A=
k=
Lamda=
1
1
6.28
Rad X
0
30
60
90
120
150
180
0
30.5236
61.0472
91.5708
122.0944
152.618
183.1416
K/2(x1-x2) cos(k/2(x1-x2)) Funzione
0
1
4
15.2618
-0.902109053 3.255203
30.5236
0.627601486 1.575535
45.7854
-0.230220912 0.212007
61.0472
-0.212232749 0.180171
76.309
0.61313508 1.503739
91.5708
-0.893996664
3.19692
ESITO DEL MODELLO
MATEMATICO: IL GRAFICO
1E+02
INTENSITA'
1E+02
8E+01
6E+01
4E+01
2E+01
0E+00
-2E+01
0
0,0005
0,001
X
0,0015
0,002
VERIFICA DEL MODELLO
L’immagine osservata sullo schermo mostra che
l’intensità in corrispondenza di diverse
posizioni angolari non varia con la regolarità
suggerita da una dipendenza di tipo seno o
coseno.
INFATTI...
VERIFICA DEL MODELLO
Le misure della distribuzione angolare di
intensità suggeriscono una dipendenza più
complessa. La linea che le rappresentata è
irregolare.
CONSIDERAZIONI
Per quali aspetti i due grafici si differenziano?
Il fenomeno osservato e misurato dipende
fortemente dalla diffrazione: infatti le
fenditure, anche se piccolissime, hanno
ampiezza di due ordini di grandezza
maggiore della lunghezza d’onda della luce
PROVIAMO...
Cosa accade se nel modello teniamo
conto della diffrazione?
Costruiamo un modello matematico per la
diffrazione.
 Costruiamo un modello che tenga conto dei
due effetti combinati.

GRAFICO ESITO DEL
MODELLO DI DIFFRAZIONE
Intensità
Diffrazione
-1000
-500
1.2
1
0.8
0.6
0.4
0.2
0
-0.2 0
Angolo (rad)
500
1000
GRAFICO ESITO DEL
MODELLO DI INTERFERENZA
1E+02
INTENSITA'
1E+02
8E+01
6E+01
4E+01
2E+01
0E+00
-2E+01
0
0,0005
0,001
X
0,0015
0,002
GRAFICO DIFFRAZIONE +
INTERFERENZA
1.60
1.40
1.20
1.00
0.80
0.60
0.40
0.20
0.00
-15
-10
-5
-0.20
0
5
10
15
CONSIDERAZIONI FINALI
L’esito della simulazione in Excel conferma che il
fenomeno studiato non riguarda solamente
l’interferenza, ma anche la diffrazione.
Il grafico ottenuto come risultato della simulazione
che tiene conto dei due modelli, corrisponde
proprio alla somma del modello dell’interferenza
e di quello della diffrazione.
PUNTATORE LASER
BACK
DOPPIA FENDITURA
BACK
CALCOLATORE CON
INTERFACCIA
BACK
SENSORE DI INTENSITA’
LUMINOSA
BACK
SENSORE DI POSIZIONE
ANGOLARE
BACK
PRINCIPIO DI
SOVRAPPOSIZIONE
L’immagine mostra
l’interferenza tra due
sorgenti puntiformi:
le linee nere rappresentano
una successione di massimi,
mentre le linee bianche
rappresentano una
successione di minimi;
-punti minimi: x=(2n+1)/2
-punti massimi: x=2n/2
BACK