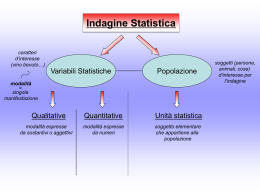
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Introduzione
Fenomeno, unità e popolazione
La statistica è una disciplina che offre una metodologia scientifica con la quale
trattare quantitativamente fenomeni che si presentano con una molteplicità di
manifestazioni e che sono osservabili sia nelle scienze naturali che in quelle sociali.
I fenomeni d’interesse per la Statistica sono detti fenomeni statistici.
Esempi di fenomeni statistici che riguardano le scienze sociali possono essere:
il “genere” delle persone di un collettivo di interesse;
il “ numero di esami” registrati sul libretto degli studenti iscritti ad un certo anno di
un dato corso di laurea;
la “temperatura massima giornaliera registrata a Ferrara” nei giorni di un certo mese
di un dato anno.
Ogni fenomeno statistico , che indicheremo con le lettere X, Y, Z, si manifesta
secondo diverse modalità che indicheremo con x, y, z, ad esempio per il fenomeno
“genere” le modalità sono maschio e femmina; per il fenomeno “numero di esami” le
modalità possono essere 0,1,2.e così via,; per il fenomeno “temperatura massima”
avremo 30°C, 35°C e così via.
Le entità su cui è possibile osservare e registrare le diverse manifestazioni x del
fenomeno X in esame sono chiamate unità statistiche. Negli esempi precedenti le
unità statistiche sono individui mentre nell’esempio delle temperature sono i giorni
del mese.
Chiameremo popolazione statistica o universo U l’insieme delle unità statistiche
sulle quali interessa studiare il fenomeno.
Relativamente agli esempi precedenti, possiamo quindi esprimerli velocemente come
Fenomeno statistico di interesse X: genere.
Popolazione statistica U: collettivo di persone.
x, modalità di manifestazione del fenomeno X, osservabili su ogni unità statistica che
compone U x: maschio o femmina:
Fenomeno statistico di interesse Y: numero di esami.
U: studenti del terzo anno del corso di laurea in ortottica ed oftalmologia.
y, Modalità di manifestazione del fenomeno Y: 0, 1, 2, 3…
Fenomeno statistico di interesse Z: temperatura massima a Ferrara.
U: giorni del mese di giugno 2015
Z, modalità di manifestazione del fenomeno Z: 30°C, 29°C, 32°C …..
Il numero di unità statistiche che compongono la popolazione statistica è chiamato
dimensione di U useremo la lettera N. I fenomeni di interesse si manifestano in
genere su popolazioni finite ma anche su popolazioni infinite cioè composte da un
1
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
numero infinito di unità statistiche. Talvolta la dimensione N di U pur essendo finita
è talmente elevata che ai fini dell’analisi statistica è conveniente pensarla infinita.
In base alle definizioni di unità e di popolazione statistica, possiamo dire che un
fenomeno statistico X è una caratteristica della popolazione statistica che si presenta
con modalità diverse a seconda della natura del fenomeno. Possono essere: un
numero nullo o intero positivo come nell’esempio del numero di esami, un numero
reale e dotato di unità di misura come nell’esempio della temperatura o altro ancora
come vedremo più avanti. Dunque i fenomeni collettivi non sono tutti uguali e
bisogna individuarne la natura ossia bisogna imparare a classificare i fenomeni
statistici
Analisi statistica di un fenomeno
Una volta stabilito:
 Il fenomeno che interessa studiare
 La popolazione su cui interessa studiarlo
 Le unità statistiche sulle quali sono reperibili le sue diverse manifestazioni,
bisogna trattare quantitativamente il fenomeno statistico, ossia bisogna:
 registrare le diverse manifestazioni del fenomeno. In questo modo si creano i
dati.
 Organizzare il risultato delle manifestazioni. Quando la popolazione è
numerosa, occorre organizzare i dati in tabelle e grafici in modo da renderlo
più leggibile. In questa fase si introducono le variabili statistiche e le
distribuzioni di frequenza.
 Elaborare i dati. L’obiettivo è di far emergere dai dati le informazioni che
interessano. Si tratta di sintetizzare i dati attraverso la costruzione di valori
sintetici e studiarne le eventuali relazioni statistiche con altri fenomeni
 Comunicare i risultati. E’ il momento conclusivo dell’analisi statistica. Anche
il risultato più interessante e più elegantemente elaborato è perfettamente
inutile se non è ben comunicato.
Le due funzioni della Statistica: Statistica descrittiva e Statistica
inferenziale
Una volta registrati i dati relativi al fenomeno X, la Statistica ha la funzione di
descriverli. Gli strumenti di analisi statistica adeguati a questo scopo formano la
Statistica descrittiva
La Statistica descrittiva si classifica in:
2
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
 Mono-variata o anche uni-variata che ha per oggetto la descrizione sintetica di
un solo fenomeno singolarmente rilevato.
 Bi-variata quando l’oggetto è una coppia di fenomeni congiuntamente rilevata
sulla stessa popolazione statistica, sulla stessa U.
 Multivariata se i fenomeni rilevati sulla stessa U sono più di due e l’obiettivo e
descriverne il comportamento congiunto, studiarne le relazioni.
L’analisi statistica mono- bi e multivariata, avendo scopi sensibilmente diversi,
necessita di strumenti matematici e statistici diversi. Le tre tipologie vanno quindi
trattate separatamente.
Abbiamo detto che le popolazioni statistiche sono formate da un numero molto
grande, di solito infinitamente grande di elementi diversi fra loro e quindi, se
vogliamo studiarla, dobbiamo valutare tutti gli individui componenti. Per motivi di
tempo e di costi non potendo esaminare l’intera popolazione eseguiamo le
misurazioni della caratteristica in esame su un numero limitato di individui, su un
campione. Tuttavia il valore ottenuto dai dati campionari è soggettivo perché dipende
dagli elementi inclusi e quindi varia da campione a campione e non rappresenta il
valore vero della caratteristica oggetto di studio.
Ad esempio se vogliamo esaminare l’effetto di un nuovo farmaco sulla pressione
arteriosa non possiamo esaminare tutti i pazienti ipertesi nel mondo, ma valuteremo
gli effetti del farmaco su un campione estratto dalla popolazione di riferimento e
quindi le nostre considerazioni sono necessariamente relative al campione esaminato
e non all’intera popolazione.
Se i dati sperimentali sono campionari, la statistica continua ad avere sempre la
descrizione e la comprensione del comportamento del fenomeno, ma la sua funzione
ora è più ardita: vuole estendere i risultati dell’elaborazione dai dati campionari
all’intera popolazione e quindi anche alla parte della popolazione U non osservata. Si
tratta di un’induzione dal particolare (campione) al generale (U) chiamata inferenza
statistica.
La statistica inferenziale offre metodologie che arrivano a conclusioni la cui validità è
relativa non solo al campione estratto ma anche all’intera popolazione. I dati
disponibili per l’inferenza sono scelti a caso fra la totalità dei dati che esaurirebbero
l’osservazione di U e la validità delle conclusioni è espressa in termini probabilistici.
Ecco perché alla base della statistica inferenziale vi sono elementi della teoria di
probabilità.
Per capire quindi le generalizzazioni statistiche ed i limiti di validità di tali
generalizzazioni dobbiamo dapprima esaminare le principali modalità utilizzate per
rappresentare, visualizzare e sintetizzare i dati campionari (statistica descrittiva),
introdurre alcuni elementi della teoria della probabilità ed infine discutere la verifica
di ipotesi (inferenza statistica)
Classificazione dei fenomeni statistici
3
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Abbiamo detto che i fenomeni statistici possono avere una natura diversa e che
quindi occorre classificarli.
La prima fondamentale distinzione è fra nomi e numeri, tra fenomeni qualitativi e
quantitativi.
Fenomeni qualitativi. Si manifestano nella popolazione osservata attraverso attributi
o categorie.
Esempi
X: genere
Y: squadra di calcio tifata
Z: titolo di studio
Fenomeni quantitativi. Si manifestano nella popolazione attraverso numeri, quantità.
Esempi:
X: temperatura massima giornaliera a Ferrara nel mese di giugno 2015;
Y: numero di accessi a un certo sito di Internet in un dato giorno.
In certe situazioni è necessario che le manifestazioni del fenomeno in esame possano
essere ordinate, per esempio dalla più piccola alla più grande. Le manifestazioni dei
fenomeni quantitativi possono essere sempre ordinate perché tra i numeri esiste una
relazione d’ordine naturale.
Per i fenomeni qualitativi è importante la sotto-classificazione che li distingue in base
alla possibilità di ordinarne le manifestazioni.
Fenomeni qualitativi ordinali. Sono fenomeni che pur essendo qualitativi si
manifestano con attributi e categorie che si possono ordinare secondo un qualche
criterio oggettivo e convenzionalmente accettato.
Esempio.
Fenomeno X: titolo di studio. Le sue modalità sono ovviamente categorie ma che tutti
ordiniamo allo stesso modo: scuola dell’obbligo < diploma < laurea triennale< titolo
post-laurea.
Fenomeni qualitativi nominali o categoriali. Sono tutti quei fenomeni qualitativi per i
quali non abbiamo un criterio oggettivo per ordinare le categorie con cui si
manifesta.
Esempi. X: gruppo sanguigno, Y: sesso, Z: lingua parlata
Fra i fenomeni quantitativi invece, una sotto-classificazione importante ai fini
dell’analisi statistica è tra fenomeni discreti e continui.
Fenomeni quantitativi discreti. Sono fenomeni quantitativi che possiamo enumerare.
Esempi. X: numero di esami registrati sul libretto al termine del primo anno. Y:
numero di furti di motorini denunciati a Ferrara nel 2014.
4
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Fenomeni quantitativi continui. Sono fenomeni quantitativi che si possono misurare
una volta scelta una opportuna unità di misura e con la disponibilità del corretto
strumento di misura.
Esempi. X: peso corporeo alle ore 8:00 e a digiuno. Y: temperatura massima
giornaliera a Ferrara nel mese di giugno 2015.
Il punto importante da capire è che le manifestazioni di un fenomeno quantitativo
continuo sono intervalli e che la caratteristica della numerabilità tipica dei fenomeni
discreti scompare a favore della caratteristica della continuità.
Osservazione. Abbiamo visto che un fenomeno statistico X si manifesta con modalità
x diverse a seconda della natura del fenomeno qualitativo o quantitativo. Indicheremo
tali modalità con gli stessi simboli x1, x2,….xn per tutti i fenomeni, siano essi
qualitativi o quantitativi. Ad esempio per rilevare il fenomeno X: genere, useremo la
scala x1 =femmina e x2=maschio.
Esercizi
Esercizio 1
Vero o falso?
a) Una popolazione statistica è l’insieme delle unità statistiche
b) Un fenomeno statistico è una caratteristica della popolazione
c) L’unità statistica è un numero
d) Un fenomeno statistico si manifesta con la stessa modalità su ciascuna unità
e) La popolazione statistica è necessariamente finita
f) La statistica è un insieme di metodologie per il trattamento scientifico dei dati
a)Vero
b) Vero
c) Falso
d) Falso
e) Falso
f) Vero
Esercizio 2
Si identifichi se le seguenti variabili sono quantitative o qualitative. Se sono
quantitative si stabilisca se la variabile è discreta o continua. Se sono qualitative, si
stabilisca se la variabile è nominale oppure ordinale.
a. I voti scolastici espressi in lettere (sistema anglosassone)
b. Il numero di lesioni subite in una caduta
c. La marca degli antidepressivi.
d. L’indice di massa corporeo (sottopeso, normale sovrappeso, obeso)
e. Il numero di crimini commesso
f. Il sesso
g. Lo stadio di maturazione dei frutti (acerbo, maturo, molto maturo)
h. Il peso alla nascita
5
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Risposte a) qualitativa ordinale; b) quantitativa discreta; c) qualitativa nominale; d)
qualitativa ordinale e) quantitativa discreta; f) qualitativa nominale g) qualitativa
ordinale; h) quantitativa continua.
Esercizio 3
Quali delle sottoelencate variabili sono qualitative e quali sono quantitative e nel
secondo caso specificare se continue o discrete.?
a) sesso
b) pressione sanguigna
c) diagnosi
d) altezza.
e) Concentrazione di glucosio nel sangue
f) Dimensione del nucleo familiare.
Sesso e diagnosi sono variabili qualitative; l’altezza, la pressione sanguigna, la
concentrazione di glucosio nel sangue sono variabili quantitative continue; la
dimensione del nucleo familiare è qualitativa discreta.
Esercizio 4
Scegliere la risposta più corretta.
1. l’insieme dei metodi statistici per la raccolta, l’organizzazione, la sintesi e la
presentazione dei dati osservati su una popolazione è
 statistica descrittiva
 un esempio di statistica
 inferenza statistica
 lo studio della statistica
2. Un fenomeno statistico è
 Una misura
 Un insieme di unità statistiche
 Un insieme di modalità osservabili
 Un’osservazione
3. La modalità di un fenomeno è:
 Un campione statistico
 La manifestazione del fenomeno su una singola unità statistica
 Una caratteristica della popolazione di riferimento.
1. l’insieme dei metodi statistici per la raccolta, l’organizzazione, la sintesi e la
presentazione dei dati osservati su una popolazione è
6
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
la statistica descrittiva
2. Un fenomeno statistico è
un insieme di modalità osservabili
3. La modalità di un fenomeno è:
la manifestazione del fenomeno su una singola unità statistica
7
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Parte I
Statistica descrittiva monovariata
Vogliamo descrivere un solo fenomeno statistico X ossia una sola caratteristica di
una popolazione statistica.
Il risultato di rilevazione del fenomeno X sulla popolazione di riferimento U è un
insieme di osservazioni formato dalle modalità xi con cui si presenta il fenomeno e
prende il nome di dati grezzi . Poiché i dati non sono ordinati, tale insieme non aiuta
o aiuta pochissimo al raggiungimento della descrizione del fenomeno X. La prima
basilare sintesi consiste nel dare una struttura ai dati grezzi organizzandoli in tabelle
e grafici
Parleremo quindi di distribuzioni di frequenze e variabili statistiche.
Distribuzioni di frequenze.
Effettuando una semplice operazione di conteggio delle modalità di X che si
ripetono, i dati grezzi vengono organizzati in una tabella.
La caratteristica in esame la chiamiamo variabile statistica e le modalità con cui si
presenta tale caratteristica sono i valori 𝑥1 , 𝑥2 , … . 𝑥𝑛 della variabile statistica.
Il numero delle volte con cui si presenta una data modalità della caratteristica è detto
frequenza assoluta di quella modalità. Indicheremo la generica frequenza assoluta
con 𝑓𝑖 . L’insieme delle frequenze (assolute) è detta distribuzione di frequenze
assolute del fenomeno X su U.
In senso generale una distribuzione di frequenza si presenta mediante una tabella di
questo tipo:
𝑥1 𝑥2 𝑥3 ………….. 𝑥𝑛
𝑓1 𝑓2 𝑓3
𝑓𝑛
8
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
In questo modo i dati sono più organizzati e meglio leggibili. La prima riga è relativa
alle modalità 𝑥𝑖 ed ha a che fare con il fenomeno X e quindi a seconda della natura
del fenomeno può contenere attributi, categorie, numeri, intervalli. La seconda riga è
relativa alle frequenze (assolute) ha invece a che fare con le unità statistiche e dunque
con la popolazione U. Costituisce la distribuzione di frequenze.
Frequenze relative e percentuali.
Le frequenze assolute sono direttamente influenzate dalla numerosità della
popolazione: più è grande la numerosità , più grandi sono le frequenze assolute., Se
l’obiettivo è confrontare le distribuzioni di frequenze di X in due o più popolazioni
con numerosità diversa occorre togliere le frequenze assolute dall’influenza della
numerosità. Si deve costruire la distribuzione delle frequenze relative. La frequenza
relativa associata alla modalità 𝑥𝑖 è il rapporto tra la frequenza assoluta di 𝑥𝑖 e la
numerosità dei dati. Le percentuali sono le frequenze relative moltiplicate per 100. Le
percentuali sono sempre comprese tra 1 e 100 e la loro somma è 100.
Frequenze assolute, frequenze relative e percentuali sono costruibili per qualunque
tipo di fenomeno X. Quando il fenomeno è almeno ordinale (cioè qualitativo ordinale
oppure quantitativo) possiamo aumentare il livello di analisi e costruire un ulteriore
tipo di distribuzione di frequenze.
Frequenze cumulate
Quando X è almeno ordinale è buona pratica costruire la v.s. ordinando in senso
crescente le modalità osservate partendo dal minimo e arrivando al massimo. La
possibilità di stabilire un ordine oggettivo e universale fra le modalità di X è utile
all’analisi statistica e consente di porsi domande come: quante sono le unità
statistiche fra tutte quelle osservate che che manifestano una modalità non più
grande ( cioè al più pari a) una certa 𝑥𝑖 ? Si tratta di sommare, cioè cumulare, le
frequenze associate alle modalità inferiori ad 𝑥𝑖 , costruendo le frequenze cumulate.
Possiamo avere la distribuzione delle frequenze cumulate assolute o relative.
Densità di frequenza
Limitiamo ora la nostra attenzione ai fenomeni quantitativi continui. Se la X è
continua le modalità 𝑥𝑖 sono intervalli. In questo caso la v.s. ci informa che al
generico intervallo 𝑥𝑖 : 𝑥𝑙 − 𝑥𝐿 appartengono 𝑓𝑖 unità statistiche. Questo è tutto ciò
che sappiamo. Non sappiamo esattamente in quale degli infiniti punti che
appartengono all’intervallo si posiziona ciascuna delle 𝑓𝑖 . Ogni volta che ci si trova in
situazioni di questo tipo, per superare l’ostacolo si formulano delle ipotesi. Due sono
le ipotesi comunemente fatte:
9
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
1) Ipotesi del valore centrale. Le 𝑓𝑖 unità statistiche che cadono nell’intervallo
𝑥𝑖 vengono associate tutte nel punto centrale dell’intervallo. Il valore centrale è
la semisomma dei suoi estremi
𝑥𝑙 + 𝑥𝐿
𝑥𝑖∗ =
2
2) Ipotesi di distribuzione uniforme. Se non conosciamo dove sono posizionate le
𝑓𝑖 unità statistiche all’interno dell’intervallo, le distribuiamo in modo uniforme
ed equidistante lungo tutto l’intervallo.
Un secondo aspetto su cui bisogna soffermarsi quando si ha a che fare con fenomeni
continui riguarda il fatto che gli intervalli possono avere ampiezza diversa.
(L’ampiezza dell’intervallo è la differenza tra l’estremo superiore e l’estremo
inferiore.) Intuiamo tutti che tanto più un intervallo è ampio quanto più conterrà più
casi di un intervallo meno ampio. Per togliere questa dipendenza introduciamo la
densità di frequenza (assoluta) che è il rapporto tra la frequenza (assoluta/relativa) e
l’ampiezza dell’intervallo:
𝑓𝑖
𝜑𝑖 =
𝑥𝐿 − 𝑥𝑙
oppure, se abbiamo N dati le densità di frequenza relativa è
𝜑𝑖
𝑁
Esempi
Supponiamo che i dati siano puramente qualitativi, ossia nominali e ordinali. Il modo
più semplice di trattarli è contare il numero dei casi che cadono in un particolare
gruppo. Per esempio, nell’analisi del censimento di una popolazione di un ospedale
psichiatrico una delle variabili di interesse è la diagnosi principale relativa al
paziente. Le classi (categorie) di questa variabile qualitativa nominale sono:
schizofrenia, disordini affettivi, sindrome mentale, subnormalità, alcolismo, altro. Per
riassumere i dati si conta il numero di pazienti per ciascun tipo di diagnosi. I risultati
vengono raccolti in una tabella detta tabella statistica, simile a questa:
Tabella 1.
Diagnosi
Numero di pazienti
Schizofrenia
474
Disordini affettivi 277
Sindrome mentale 405
Subnormalità
58
Alcolismo
57
Altro
196
TOTALE
1467
10
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Il numero di pazienti sta ad indicare la frequenza assoluta della classe. Così la
frequenza assoluta della schizofrenia è 474. L’insieme delle frequenze di tutte le
possibili caratteristiche è detta distribuzione di frequenze della variabile.
Nella tabella successiva viene mostrata la distribuzione di frequenze di una variabile
quantitativa: la parità ovvero il numero di gravidanze precedentemente condotte a
termine per un campione di donne che si prenotano per il parto ad un dato ospedale.
In questo caso sono ammessi soltanto determinati valori della variabile, dal momento
che il numero di gravidanze deve necessariamente essere intero. Quindi la variabile è
quantitativa discreta
Tabella 2.
Parità
Frequenza
0
59
1
44
2
14
3
3
4
4
5
1
TOTALE 125
Per ottenere la distribuzione di frequenza di una variabile quantitativa continua è
necessario scomporre i valori delle osservazioni in una serie di intervalli distinti non
sovrapposti. Sebbene non sia necessario, conviene scegliere gli intervalli con la stessa
ampiezza per facilitare il confronto fra le classi. Una volta selezionati i limiti
superiore ed inferiore di ciascun intervallo, si calcola il numero dei dati grezzi della
variabile continua i cui valori rientrano in ciascuna coppia di limiti e si ottiene la
tabella distribuzione di frequenza.
La tabella 3 mostra i dati grezzi di una variabile quantitativa continua: il volume
espiratorio forzato (FEV1) in litri, in un campione di 57 studenti di medicina di sesso
maschile.
2.85
2.85
2.98
3.04
3.10
3.19
3.20
3.30
3.39
3.42
3.50
3.54
3.54
3.57
3.60
3.69
3.70
3.70
3.75
3.78
Tabella 3.
3.90 4.14
3.96 4.16
4.05 4.20
4.08 4.20
4.10 4.30
4.32
4.44
4.47
4.47
4.47
4.50
4.56
4.68
4.70
4.71
4.80 5.20
4.80 5.30
4.90 5.43
5.00
5.10
11
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
3.10 3.48 3.60 3.83 4.14 4.30 4.50 4.78 5.10
Per ottenere una distribuzione di frequenze assolute utilizzabile è necessario dividere
la scala dei possibili volumi espiratori in intervalli, ciascuno dei quali verrà
identificato con una classe (ad esempio da 3.0 a 3.5, da 3.5 a 4.0, e così via) e
contare il numero di individui il cui valore di FEV1 appartiene ad ogni classe. E’
necessario che le classi non si sovrappongano, pertanto bisogna decidere quale tra
due intervalli contigui, debba contenere il valore soglia, al fine di evitare conteggi
duplici. Per convenzione si è soliti includere l’estremo inferiore nell’intervallo , e
attribuire invece l’estremo superiore all’intervallo successivo. Quindi l’intervallo che
va da 3.0 a 3.5 include 3.0 ma non 3.5. Con riferimento alla tabella 3, se scegliamo di
partire da 2.5 con intervalli di ampiezza 0.5 otteniamo la distribuzione di frequenze
mostrata in tabella 4. Si noti che la distribuzione di frequenze non è unica. Se infatti
anziché partire da 2.5 scegliamo come valore di partenza 2.4 con intervalli di
ampiezza 0.2, la distribuzione di frequenze risultante sarà diversa.
Tabella 4.
FEV1
Frequenza Frequenza
Relativa %
2.0 - 2.5 0
0.0
2.5 – 3.0 3
5.3
3.0 – 3.5 9
15.8
3.5 – 4.0 14
24.6
4.0 – 4.5 15
26.3
4.5 – 5.0 10
17.5
5.0 – 5.5 6
10.5
5.5 - 6.0 0
0.0
TOTALE 57
100.0
E’ evidente che quest’ultima tabella permette una migliore comprensione dei dati
rispetto alla tabella dei dati grezzi. Nella tabella vengono calcolate anche le frequenze
relative. Per capirne l’utilità consideriamo il seguente esempio.
In tabella 5 vengono mostrati come si distribuiscono i valori di colesterolo sierico di
1067 soggetti della popolazione maschile degli Stati Uniti di età compresa tra 25 e 34
anni nei rispettivi intervalli
Tabella 5.
Livello di colesterolo Numero di soggetti
(mg/100mL)
80-119
13
120-159
150
160 -199
442
200-239
299
12
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
240-279
280-319
320-359
360-399
TOTALE
115
34
9
5
1067
In una distribuzione di frequenza è utile, a volte, conoscere non tanto il numero
assoluto dei valori che rientrano in un dato intervallo (frequenza assoluta) quanto la
proporzione dei valori (frequenza relativa). La frequenza relativa per un intervallo è
calcolata dividendo il numero di osservazioni all’interno di un intervallo per il
numero totale di osservazioni della tabella.
La frequenza relativa può essere espressa anche in valori percentuali (%). Ad
esempio nella tabella 5 la frequenza relativa nella classe 80-119 mg/100mL è
(13⁄1067) = 0.012 = 1.2%; allo stesso modo, la frequenza relativa nella classe
120-159 mg/mL è (150⁄1067) = 0.141 = 14.1%. Le frequenze relative per tutti gli
intervalli di una tabella si sommano al 100%.
Le frequenze relative sono utili per confrontare serie di dati con numero diverso di
osservazioni. La tabella 6 mostra le frequenze assolute e relative del livello di
colesterolo sierico per i 1067 soggetti della popolazione maschile di età compresa tra
25 e 34 anni già illustrata in tabella 5 e per un gruppo di 1227 maschi di età
compresa tra 55 e 64 anni. Poiché i soggetti anziani sono più numerosi non è corretto
confrontare le colonne delle frequenze assolute dei due gruppi. Invece il confronto
delle frequenze relative ha un significato. Possiamo notare che, in generale, i soggetti
anziani presentano livelli di colesterolo sierico più elevati rispetto ai giovani; i
soggetti giovani hanno una proporzione più elevata di valori al di sotto di
200mg/100mL, mentre gli anziani presentano una proporzione più elevata al di sopra
di questo valore.
Tabella 6.
Livello di
colesterolo
(mg/100mL)
80-119
120-159
160-199
200-239
240-279
280-319
320-359
360-399
Età 25-34
Numero di
soggetti
13
150
442
299
115
34
9
5
Frequenza
relativa (%)
1.2
14.1
41.4
28.0
10.8
3.2
0.8
0.5
Età 55-64
Numero di
soggetti
5
48
265
458
281
128
35
7
Frequenza
relativa (%)
0.4
3.9
21.6
37.3
22.9
10.4
2.9
0.6
13
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Totale
1067
100.0
1227
100.0
La frequenza relativa cumulativa per un intervallo è la percentuale del numero totale
di osservazioni che hanno un valore inferiore o uguale al limite superiore
dell’intervallo stesso. La frequenza relativa cumulativa è calcolata sommando le
frequenze relative per l’intervallo specificato assieme a quelle per tutti gli intervalli
precedenti. Così per il gruppo di età compresa tra 25 e 35 anni la frequenza relativa
cumulativa del secondo intervallo è 1.2+14.1=15.3%; allo stesso modo, la frequenza
relativa cumulativa del terzo intervallo è 1.2+14.1+41.4=56.7%. Come le frequenze
relative, le frequenze relative cumulative sono utili per confrontare serie di dati che
contengono numeri diversi di osservazioni. La tabella 7 riporta le frequenze relative
cumulative dei livelli di colesterolo sierico dei due gruppi di maschi illustrati nella
tabella 6.
Tabella 7.
Età 25-34
Livello di
colesterolo
(mg/100mL)
Frequenza
relativa(%)
80-119
120-159
160-199
200-239
240-279
280-319
320-359
360-399
1.2
14.1
41.4
28.0
10.8
3.2
0.8
0.5
Frequenza
relativa
cumulativa (%)
1.2
15.3
56.7
84.7
95.5
98.7
99.5
100
Età 55-64
Frequenza
relativa (%)
0.4
3.9
21.6
37.3
22.9
10.4
2.9
0.6
Frequenza
relativa
cumulativa (%)
0.4
4.3
25.9
63.2
86.1
96.5
99.4
100
In accordo con la tabella precedente, i soggetti anziani tendono ad avere livelli di
colesterolo sierico più elevati dei giovani. Ciò è più evidente nella tabella 7 che in
tabella 6. Ad esempio il 56.7% dei soggetti di età compresa tra 24 e 34 anni ha un
livello di colesterolo sierico inferiore o uguale a 199 mg/100 mL, mentre solo il 25.9
% dei soggetti di età compresa tra 55 e 64 anni rientra in questa categoria.
14
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Rappresentazione grafiche
Con le distribuzioni di frequenze (assolute, relative o percentuali, e cumulate)
possiamo costruire grafici. La rappresentazione grafica delle distribuzioni di
frequenze è alternativa alla forma tabellare. Non si tratta di effettuare una sintesi ,
ma di presentare i dati in diversa forma.
Sono disponibili molti metodi per visualizzare graficamente le distribuzioni di
frequenza, a seconda che la variabile sia qualitativa o quantitativa discreta o continua
Come è stato detto la frequenza di un valore di una variabile in un campione è il
numero di volte con cui è stato osservato quel particolare valore e la distribuzione di
frequenze di una variabile visualizza le frequenze di tutti i suoi valori.
Per visualizzare graficamente le distribuzioni di frequenza di una variabile qualitativa
si utilizza un diagramma a barre. In tale rappresentazione si impiegano barre
rettangolari aventi uguale larghezza ed altezza uguale alla frequenza In figura 1
vengono rappresentati i dati della variabile qualitativa nominale “diagnosi principali
in un ospedale psichiatrico” già tabulati in tabella 1.
Diagnosi principali in un ospedale
psichiatrico
altro
alcolismo
subnormalità
Sindrome mentale
disordini affettivi
Schizofrenia
0
100
200
300
400
500
Figura 1. Diagramma a barre che mostra le diagnosi principali in un ospedale
psichiatrico.
Se la distribuzione si presenta secondo un carattere quantitativo discreto, questa può
essere rappresentata ponendo sull’asse delle ascisse le modalità, ossia i valori della
variabile, e sull’asse delle ordinate le frequenze in modo tale che l’insieme dei punti
d’incontro tra le modalità e le relative frequenze, individuati dalle coordinate
cartesiane, rappresenti la distribuzione. Si ottiene così il diagramma cartesiano. La
figura 2 rappresenta i dati della variabile quantitativa discreta tabulata in tabella 2.
15
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
70
F
r
e
q
a
u
e
n
z
60
50
40
30
20
10
0
0
1
2
3
4
5
6
Parità
Figura 2. Parità di donne prenotatesi per il parto in un ospedale (vedi testo)
Istogrammi
Il modo più comune per rappresentare una distribuzione di frequenze per una
variabile continua è l’istogramma.
Un istogramma utilizza l’area di barre rettangolari per visualizzare la distribuzione di
frequenza. E’ un diagramma che vede indicati sull’asse orizzontale gli estremi degli
intervalli che rappresentano le classi di suddivisione della variabile quantitativa
continua. In corrispondenza di ciascun intervallo è costruito un rettangolo la cui base
è uguale all’ampiezza dell’intervallo e la cui altezza si può calcolare tenendo presente
che l’area 𝐴 di ogni rettangolo deve essere proporzionale alla frequenza
corrispondente all’intervallo stesso, ossia, se la frequenza è 𝑓 e la costante di
proporzionalità è 𝑘, si ha
𝐴 = 𝑘𝑓
Per semplificare il problema si pone k=1 e quindi l’area di ogni rettangolo ha un
significato preciso: è interpretabile come frequenza.
𝐴=𝑓
Tuttavia, essendo l’area del rettangolo uguale alla base 𝑏 per l’altezza ℎ, quest’ultima
risulta
𝑓
ℎ=
𝑏
ossia l’altezza risulta uguale alla densità di frequenza. Concludendo in un istogramma
sulle ascisse si mettono gli intervalli della variabile statistica, sulle ordinate la densità
di frequenza. Si tenga sempre presente che il termine istogramma va riservato solo a
diagrammi la cui area è interpretabile come frequenza (assoluta o relativa).
Per chiarire ulteriormente le idee consideriamo il seguente esempio.
16
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Supponiamo di avere una variabile quantitativa che ha la seguente distribuzione di
frequenza
X 26-30 30-34 34-42 42-52 52-57 57-65
f
40
72
120
20
20
10
Se rappresentassimo sulle ordinate le frequenze e sulle ascisse gli intervalli, si
otterrebbe la seguente rappresentazione:
140
F
r
e
z
q
a
u
e
n
120
100
80
60
40
20
0
26-30
30-34
34-42
42-52
52-57
57-65
Questa rappresentazione falsa completamente la percezione del fenomeno. Due classi
hanno la stessa frequenza ma una ha ampiezza doppia dell’altra e quindi le stesse
frequenze sono distribuite diversamente nelle rispettive classi. Questo non risulta dal
grafico. Bisogna tenere conto di questo aspetto.
La funzione densità di frequenza si ottiene dividendo le frequenze per l’ampiezza
dell’intervallo. Si ha quindi la seguente tabella:
X
26-30 30-34 34-42 42-52 52-57 57-65
Densità 10
18
15
2
4
1.25
e il suo istogramma è il seguente:
17
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
20
D
f
e
r
e
n
d
q
s
i
u
i
e
t
à
…
18
16
14
12
10
8
6
4
2
0
26-30
30-34
34-42
42-52
52-57
57-65
Età
Figura 3.
Riprendendo la tabella 4 e tenendo conto dell’ampiezza dell’intervallo si ha
Tabella 8. Distribuzione della densità frequenze di FEV1
FEV1 Frequenza Densità di frequenza
2.0 - 2.5
0
0.0
2.5 – 3.0
3
6.0
3.0 – 3.5
9
18
3.5 – 4.0
14
28
4.0 – 4.5
15
30
4.5 – 5.0
10
20
5.0 – 5.5
6
12
5.5 - 6.0
0
0.0
E l’istogramma corrispondente è rappresentato in figura 3 .
Figura 4. Rappresentazione della densità di frequenze per i dati FEV
18
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
35
D
e
n
s
i
t
à
f30
r25
e
q20
u15
e
10
n
z5
d
e0
i
2.0
2.5
3.0
3.5
4.0
4.5
5.0
5.5
FEV1 (litri)
Possiamo anche rappresentare la densità di frequenze cumulative di questa variabile
quantitativa. Si ha la seguente tabella:
Tabella 8. Distribuzione della densità frequenze cumulative di FEV1
FEV1 Frequenza Frequenze cumulative
2.0 - 2.5
0
0.0
2.5 – 3.0
3
3
3.0 – 3.5
9
12
3.5 – 4.0
14
26
4.0 – 4.5
15
41
4.5 – 5.0
10
51
5.0 – 5.5
6
57
5.5 - 6.0
0
57
e la corrispondente rappresentazione è
19
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
70
F
r
e
q
u
e
n
z
e
c
u
m
u
l e
a
t
i
v
60
50
40
30
20
10
0
0
2
4
6
8
10
FEV1(Litri)
Figura 4 Rappresentazione del poligono delle frequenze cumulative dei dati FEV1.
Abbiamo esaminato le distribuzioni di frequenza e le distribuzioni di frequenza
cumulative. Abbiamo già detto che quando si vogliono confrontare due o più serie di
dati, queste ultime sono più adatte rispetto alle distribuzioni di frequenza perché si
possono facilmente sovrapporre. Nella figura sottostante vengono confrontate le
frequenze cumulative relative ai livelli di colesterolo sierico per soggetti della
popolazione maschile di età compresa tra 25 e 34 anni e età compresa tra 55 e 64 anni
(vedi tabella 7)
120
F
r
e
q
u
e
n
z
a
c
u
m
u
l
a
t
i
v
a
100
80
60
40
20
0
79.5 119.5 159.5 199.5 239.5 279.5 319.5 359.5 399.5
Livelli colesterolo (mg/100mL)
Le distribuzioni di frequenza cumulativa possono essere utilizzate anche per ottenere
i percentili o i quartili di una serie di dati. Sono quei valori del carattere osservato
20
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
che dividono la distribuzione in 100 parti oppure in 4 parti uguali. Sono
rispettivamente 3 e 99 valori. Ad esempio il 95-esimo percentile è il valore che è
maggiore o uguale al 95% delle osservazioni e minore o uguale al restante 5%. Nella
figura il cinquantesimo percentile (oppure il secondo quartile) dei livelli di
colesterolo sierico per il gruppo di età compresa tra 25 e 34 anni- cioè il valore
maggiore o uguale alla metà delle osservazioni e minore o uguale all’altra metà- è
approssimativamente 193 𝑚𝑔⁄100 𝑚𝐿; il 50-esimo percentile per il gruppo di età
compresa tra 55 e 64 anni è circa 226𝑚𝑔⁄100𝑚𝐿.
Aerogrammi o diagrammi circolari
L’aerogramma è una rappresentazione equivalente a un diagramma a barre adatta a
fenomeni qualitativi. In un aerogramma le frequenze relative ad ogni categoria sono
rappresentate dividendo un cerchio in settori, in modo che ogni settore sottenda un
angolo proporzionale alla frequenza relativa alla categoria corrispondente. Se
l’ampiezza dell’angolo giro è di 360° , l’ampiezza dell’angolo 𝛼 relativo ad ogni
singola frequenza misurata in gradi , si ricava da una elementare proporzione
𝛼: 360 = 𝑓𝑖 : 𝐹
ove 𝐹 è la frequenza totale e 𝑓𝑖 è la frequenza assoluta della i-esima categoria.
Risolvendo rispetto ad 𝛼 si ottiene
𝑓𝑖
𝛼 = 360 = 360𝑓𝑟
𝐹
ove 𝑓𝑟 è la frequenza relativa dell’ì-esima categoria. Per ottenere l’angolo in gradi di
ogni singola categoria è sufficiente moltiplicare la frequenza relativa per 360. La
tabella 9 mostra una parte dei dati relativi ai decessi femminili suddivisi per causa in
Inghilterra e Galles ed i calcoli necessari per costruire il corrispondente aerogramma.
Tabella 9
Cause di morte
Frequenza Frequenza
relativa
Malattie del sistema circolatorio 137165
0.46619
Neoplasie
69948
0.23773
Malattie del sistema respiratorio 33223
0.11292
Lesioni ed avvelenamenti
6427
0.02184
Malattie del sistema digerente
10779
0.03663
Malattie del sistema nervoso
5990
0.02936
Altro
30695
0.10432
Angolo
(gradi)
168
86
40
8
13
7
38
21
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
TOTALE
294227
1.00000
360
1
2
3
4
5
6
7
Figura 5 Principali cause di morte in Inghilterra e Galles nel 1983.
Esercizi
Esercizio 1
I seguenti tre fenomeni sono stati rilevati su 16 famiglie residenti nel nord Italia
X: regione di provenienza (F=Friuli, L=Lombardia, P=Piemonte, V=Veneto)
L V V L P F F L V F F P L F L V
Y: titolo di studio del/la capofamiglia (N=nessuno, E=licenza elementare, M=licenza
media, D=diploma, L=laurea, A=titolo post laurea)
D E M L A M M L D D D E D N E D
Z: numero di immobili di proprietà
0 1 2 1 1 0 0 0 1 3 2 0 1 0 0 2
Per ciascun fenomeno organizzare il risultato della rilevazione in forma tabellare
costruendo la variabile statistica con le distribuzioni di frequenze assolute e relative e
22
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
indicare quale rappresentazione grafica mette il evidenza l’importanza relativa fra le
modalità.
Variabile statistica X: Regione di provenienza
𝑥𝑖
𝑓𝑖
𝑓𝑖 ⁄𝑁
Friuli
5 5⁄16 =0.3125
Lombardia 5 5⁄16 =0.3125
Piemonte 2 2⁄16 = 0.125
Veneto
4 4⁄16 = 0.25
16
1
Variabile statistica Y: titolo di studio del/la capofamiglia
𝑦𝑖
𝑓𝑖
𝑓𝑖 ⁄𝑁
Nessuno
1 1⁄16 =0.0625
Elementari 3 3⁄16 =0.1875
Medie
3 3⁄16 =0.1875
Diploma
6 6⁄16 =0.375
Laurea
2 2⁄16 =0.125
Post -laurea 1 1⁄16 =0.0625
16
1
Variabile statistica Z: numero di immobili di proprietà
𝑧𝑖 𝑓𝑖
𝑓𝑖 ⁄𝑁
0 7 7⁄16 =0.4375
1 5 5⁄16 =0.3125
2 3 3⁄16 = 0.1875
3 1 1⁄16 = 0.0625
16
1
La rappresentazione grafica che mette in evidenza l’importanza relativa fra le
modalità è il grafico a torta.
Esercizio 2.
Vero o falso?
a) La variabile statistica è l’insieme delle modalità osservate con le corrispondenti
frequenze.
b) Per i fenomeni categoriali non è possibile la costruzione delle frequenze
relative
23
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
c) Le frequenze assolute sono numeri interi la cui somma riproduce la numerosità
della popolazione
d) Le frequenze relative sono sempre comprese tra 0 e 1 e la loro somma è
unitaria.
e) Per effettuare confronti sono sempre necessarie le frequenze relative (o
percentuali)
f) Un grafico a barre e un istogramma sono la stessa cosa
g) Per rappresentare graficamente un fenomeno quantitativo continuo (rilevato in
intervalli di diversa ampiezza) si devono utilizzare le densità e non le
frequenze.
h) Le frequenze cumulate sono calcolabili per qualunque fenomeno
a)V b) F c)V d)V e) F f) F g)V h) F
Esercizio 3
1. La somma delle frequenze relative è:
 Dipende dal tipo di fenomeno qualitativo o quantitativo
 La numerosità della popolazione
 1
 100
2. Il grafico più corretto per rappresentare la distribuzione di frequenze di un
fenomeno quantitativo continuo è:
 Un diagramma a bastoncini con le modalità sulle ascisse e le frequenze sulle
ordinate
 Un istogramma con gli intervalli sulle ascisse e le densità sulle ordinate
 Un istogramma con gli intervalli sulle ascisse e le frequenze sulle ordinate.
 Un diagramma a torta
3.



La definizione di frequenza relativa è:
Il rapporto tra la frequenza assoluta e la numerosità della popolazione
Il rapporto tra due frequenze assolute consecutive
La somma delle frequenze assolute associate alle modalità più piccole.
4. La definizione di frequenze cumulate assolute è
 La somma di due frequenze assolute consecutive
24
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
 La somma delle frequenze assolute associate alle modalità inferiori
nell’ordinamento
 La somma delle frequenze assolute associate alle modalità superiori
nell’ordinamento
1. La somma delle frequenze relative è:
1
2. Il grafico più corretto per rappresentare la distribuzione di frequenze di un
fenomeno quantitativo continuo è:
Un istogramma con gli intervalli sulle ascisse e le densità sulle ordinate
3. La definizione di frequenza relativa è:
Il rapporto tra la frequenza assoluta e la numerosità della popolazione
4. La definizione di frequenze cumulate assolute è
La somma delle frequenze assolute associate alle modalità inferiori
nell’ordinamento
Esercizio 4
Si consideri la variabile “dimissione di pazienti in un ospedale” e supponiamo di
avere la seguente tabella:
Possibilità di dimissione per i pazienti di un ospedale
Dimissione Frequenza
Impossibile
871
Possibile
339
Prossima
257
TOTALE
1467
Si identifichi il tipo di variabile e si calcoli la frequenza relativa, la frequenza
cumulata e la frequenza relativa cumulata.
La variabile “dimissione” è una variabile qualitativa e le sue categorie possono essere
ordinate. Si tratta quindi di una variabile qualitativa ordinale.
La frequenza relativa di ogni classe si ottiene facendo il rapporto tra la frequenza
assoluta della classe e il totale delle frequenze. Così per la classe “impossibile” la
frequenza relativa è 871⁄1467 = 0.594
Poiché le categorie di questa classe possono essere ordinate possiamo considerare le
frequenze cumulate. La frequenza cumulata per un valore di una variabile è il numero
di individui il cui valore è minore o uguale a quello preso in considerazione. Quindi,
se ordiniamo in maniera crescente la dismissione come “impossibile”, “possibile”,
“prossima”, le frequenze cumulate sono rispettivamente 871, 1210 (=871+339) e
25
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
1467 (1210+257). Analogamente a quanto visto prima, la frequenza relativa
cumulata per un dato valore è la proporzione di individui nel campione il cui valore è
minore o uguale a quello preso in considerazione. Nell’esempio considerato tali
valori sono 0.59 0.82 (0.59+0.23) e 1.00. Si ha quindi la seguente tabella.
Dimissione Frequenza Frequenza Frequenza Frequenza relativa
Relativa cumulata
cumulata
Impossibile
871
0.59
871
0.59
Possibile
339
0.23
1210
0.82
Prossima
257
0.18
1467
1.00
TOTALE
1467
1.00
1467
1.00
Da questa tabella possiamo dedurre che la proporzione di pazienti non in procinto di
essere dimessi, cioè la cui dimissione non è prossima, è 0.82 cioè 82%.
Esercizio 5
La tabella seguente illustra le cause di morte per infortunio di 100 bambini di età
compresa tra 5 e 9 anni. I dati sono nominali:
1 rappresenta incidente stradale,
2 annegamento,
3 incendio in ambiente domestico,
4 omicidio
5 altre cause.
Con questi dati che cosa possiamo concludere?
1
2
4
5
2
1
1
3
1
5
5
1
1
1
3
2
1
3
1
1
3
1
3
1
1
5
2
1
2
1
1 2 4 1 3 1 5
5 3 1 2 1 4 1
1 5 1 2 1 1 2
5 15 3 1 1 2 1
1 2 1 5 1 5 1
1 1 1 3 4 1 1
1 1 2 1 1 2 3
5 2 3 5 1 3 4
4 5 4 1 5 1 5
5 1 1 5 1 1 5
I dati grezzi non ci dicono nulla sulle cause di morte. Per arrivare ad una qualche
conclusione dobbiamo costruire una distribuzione di frequenza. Per i dati nominali ed
ordinali, una distribuzione di frequenza è una tabella formata da una serie di
classi/categorie con le conte numeriche che corrispondono a ciascuna di esse.
Per costruire una distribuzione di frequenza occorre elencare le diverse cause di
morte e poi contare il numero di bambini deceduti per ciascuna causa. Si ottiene la
tabella seguente:
26
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Causa
Numero di decessi
Incidente stradale
48
Annegamento
14
Incendio Domestico
12
Omicidio
7
Altro
19
TOTALE
100
Usando la tabella è possibile osservare che 48 dei 100 decessi per infortunio è per
incidenti stradali, 14 per annegamento, 12 per incendio in ambiente domestico, 7 per
omicidio e 19 per altre cause.
Oltre alla tabella possiamo utilizzare anche un grafico per visualizzare questa serie di
dati. In questo caso utilizzeremo un diagramma a barre posizionando lungo l’asse
orizzontale le classi in cui rientrano le osservazioni. Le barre verticali rappresentano
le frequenze di osservazioni in ciascuna classe. Il grafico evidenzia che un’ elevata
proporzione di decessi infantili è il risultato di incidenti stradali. Si osservi che sia la
tabella che il diagramma a barre forniscono maggiori informazioni sulle cause di
morte per infortunio di 100 bambini rispetto ad un elenco di 100 osservazioni.
Altro
Omicidio
Incendio domestico
Annegamento
Incidente stradale
0
10
20
30
40
50
60
Esercizio 6
Nel costruire una tabella, quando può essere utile utilizzare frequenze relative
anziché assolute?
Quando vogliamo confrontare serie di dati con un numero diverso di osservazioni
non è corretto confrontare le frequenze assolute, ma bisogna normalizzarle al totale
delle osservazioni, ossia considerare le frequenze relative.
Esercizio 7
27
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Quali grafici possono essere utilizzati per illustrare osservazioni nominali o ordinali?
Quali sono adatte per osservazioni discrete o continue?
Il diagramma a barre e l’ aerogramma sono grafici utilizzati per distribuzioni di
frequenza per dati nominali o ordinali; mentre l’ istogramma
e il diagramma cartesiano sono utili per rappresentare distribuzioni di frequenze per
dati quantitativi rispettivamente continui e discreti. e.
Esercizio 8
Che cosa sono i percentili di una serie di dati? Quanti sono?
Sono quei valori del carattere osservato che dividono la distribuzione in 100 parti
uguali. Sono 99 valori
Esercizio 10
Si è visto che la parità -ovvero il numero di gravidanze precedentemente condotte a
termine per un campione di donne che si prenotano per il parto ad un dato ospedale- è
una variabile quantitativa discreta e si è visto anche le sue osservazioni in un dato
ospedale sono le seguenti:
Parità
Frequenza
0
59
1
44
2
14
3
3
4
4
5
1
TOTALE
125
Si calcoli la frequenza relativa , la frequenza cumulativa e la frequenza relativa
cumulativa.
Tenendo presente la definizione di frequenza relativa, di frequenza cumulativa e di
frequenza relativa cumulativa si ha la seguente tabella
Parità
0
1
2
3
4
5
Frequenza Frequenza Frequenza Frequenza relativa
Relativa% cumulativa
Cumulativa %
59
47.2
59
47.2
44
35.2
103
82.4
14
11.2
117
93.6
3
2.4
120
96.0
4
3.2
124
99.2
1
0.8
125
100.0
28
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
TOTALE
125
100.0
125
100.0
Esercizio 11
Su un collettivo di 10 ragazze impiegate in un gruppo editoriale sono stati rilevati i
seguenti fenomeni:
X: numero di scarpe possedute
8 8 5 7 7 8 8 6 7 6
Y: colore dei capelli ( B=biondo, R =rosso, C=castano)
C B B R C B B B C C
Z: titolo di studio (M=scuola media, S=scuole superiori, U=università)
M S M U U S U S S S
Per ciascun fenomeno costruire la variabile statistica e fornire una distribuzione a
piacere tra frequenze relative e percentuali. Costruire ove sensato, la distribuzione di
frequenze cumulate.
Variabile statistica X: numero di scarpe.
La variabile è quantitativa discreta: ha senso costruire le frequenze cumulate.
𝑥𝑖 𝑓𝑖 Frequenze relative Frequenze cumulate
1
5 1
1
= 0.1
10
6 2
0.2
3
7 3
0.3
6
8 4
0.4
10
10
1
Variabile statica Y: colore dei capelli.
La variabile è qualitativa nominale: non ha senso costruire le frequenze cumulate.
𝑦𝑖
𝑓𝑖 Frequenze relative percentuali
Biondo 5
50%
Castano 4
40%
Rosso 1
10%
10
100%
Variabile statistica Z: titolo di studio
La variabile è qualitativa ordinale: ha senso costruire le frequenze cumulate.
29
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
𝑧𝑖
𝑓𝑖 Frequenze relative Frequenze cumulate
medie
2
0.20
2
superiori 5
0.5
7
università 3
0.3
10
10
1
Valori medi
Introduzione
Le tabelle e la rappresentazione grafica di un fenomeno costituiscono un notevole
strumento di illustrazione e di divulgazione ma non di sintesi dell’informazione.
Praticamente si ha l’esigenza di stabilire metodiche utili a sintetizzare le informazioni
contenute nei dati sperimentali anche se tale sintesi comporta naturalmente una
perdita di informazione. I valori medi operano delle sintesi che facilitano
l’interpretazione dei fenomeni che altrimenti si renderebbe difficoltosa se non
impossibile. Infatti si parte da una massa di dati, difficilmente interpretabile, e si
perviene ad un solo dato di facile intuizione e comprensione.
Si distinguono due tipi di valori medi: medie che si ottengono da concorso di tutti i
termini della distribuzione (medie analitiche) e medie che si ottengono da un solo
termine scelto in base ad una caratteristica (medie di posizione).
Alle medie analitiche appartengono: la media aritmetica, la media geometrica e la
media armonica.
Alle medie di posizione appartengono: la mediana o valore mediano, la moda o il
valore modale e i quantili.
La scelta dell’una o dell’altra di queste medie dipende dalle caratteristiche della
distribuzione e dall’interesse del ricercatore.
Media aritmetica
Se 𝑥1 , 𝑥2 , 𝑥3 , … . . , 𝑥𝑛 sono gli 𝑁 valori della variabile 𝑥, la media 𝑥̅ è definita dal
rapporto tra l’ammontare totale del carattere e il numero delle unità in cui è stato
rilevato, ossia
𝑥1 + 𝑥2 + ⋯ + 𝑥𝑛 ∑𝑛1 𝑥𝑖
𝑥̅ =
=
𝑛
𝑛
Ad esempio se si ha 𝑥1 = 4, 𝑥2 = 7, 𝑥3 = 9, 𝑥4 = 10, 𝑥5 = 12, la media sarà
𝑥̅ =
4 + 7 + 9 + 10 + 12 42
=
= 8.4
5
5
30
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
La media può essere utilizzata come misura di sintesi per misurazioni discrete e
continue. In genere comunque non è adatta per dati nominali o ordinali. Si ricordi che
per questi tipi di dati i numeri sono semplici etichette; così se scegliamo di indicare i
gruppi sanguigni 0, A, B, AB con i numeri 1,2,3,4, un gruppo sanguigno medio di 1.8
non ha alcun significato. Un’eccezione a questa regola si applica ai dicotomici ed i
due possibili risultati sono rappresentati con 0 e 1. In questo caso la media delle
osservazioni è uguale alla proporzione di 1 nella serie di dati. Esempio. Supponiamo
di avere un gruppo di 13 persone con una data patologia e voler conoscere la
proporzione di maschi. I valore 1 rappresenta il maschio, lo 0 la femmina.
Supponiamo di avere la seguente tabella:
Soggetto Sesso
1
0
2
1
3
1
4
0
5
0
6
1
7
1
8
1
9
0
10
1
11
1
12
1
12
0
Risulta
8
= 0.615
13
Pertanto il 61.5 dei soggetti nello studio, sono maschi
𝑥̅ =
Media di dati raggruppati (Media ponderata)
Prendiamo ora in considerazione una serie osservazioni, per esempio, i punteggi
riportati a un test attitudinale da un gruppo di 10 soggetti.
Punteggi: 4, 6, 8, 8, 7, 6, 7, 8, 8, 6 la media darà
𝑥̅ =
4+6+8+8+7+6+7+8+8+6
= 6.8
10
31
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Come si può osservare l’operazione è diventata più laboriosa della precedente e lo
sarebbe ancora di più se si dovesse calcolare la media dei punteggi ottenuti per un
numero molto più grande di soggetti. Ma osservando attentamente la distribuzione
notiamo che alcuni soggetti hanno ottenuto lo stesso punteggio e quindi possono
essere raggruppati e successivamente passare al calcolo della media aritmetica che in
questo caso si chiama media aritmetica ponderata per distinguerla da quella
precedente che viene definita media aritmetica semplice. Tenendo presente che il
punteggio 6 ha frequenza 3, il punteggio 7 ha frequenza 2, ed il punteggio 8 ha
frequenza 4, il calcolo può essere così semplificato
4+6∙3+7∙2+8∙4
= 6.8
10
In termini generali, se la variabile 𝑥 ha valori 𝑥1 , 𝑥2 ,…. 𝑥𝑘 con frequenza 𝑓1 ,
𝑓2 ……. 𝑓𝑘 , rispettivamente, la media aritmetica ponderata è calcolabile mediante
𝑥̅ =
𝑥̅ =
𝑥1 ∙ 𝑓1 + 𝑥2 ∙ 𝑓2 + ⋯ . . 𝑥𝑘 ∙ 𝑓𝑘
𝑓1 + 𝑓2 + ⋯ . 𝑓𝑘
Pertanto, la media aritmetica ponderata di una distribuzione è data dal rapporto tra la
somma dei prodotti delle modalità per la propria frequenza, diviso la somma delle
frequenze.
Indicato con 𝐹 la somma di tutte le frequenze, cioè
𝐹 = 𝑓1 + 𝑓2 + ⋯ +𝑓𝑘
La media ponderata è calcolabile con
𝑓1
𝑓2
𝑓𝑘
𝑥̅ = 𝑥1 + 𝑥2 + ⋯ + 𝑥𝑘 = 𝑥1 𝑓𝑟1 + 𝑥2 𝑓𝑟2 + ⋯ + 𝑥𝑘 𝑓𝑟𝑘
𝐹
𝐹
𝐹
𝑓𝑖
ove 𝑓𝑟𝑖 = è la frequenza relativa del generici i-esimo termine.
𝐹
In conclusione, per calcolare la media ponderata di una variabile 𝑥 con valori 𝑥1 ,
𝑥2 ,…. 𝑥𝑘 e frequenza relativa 𝑓𝑟1 , 𝑓𝑟2 ……. 𝑓𝑟𝑘 , occorre fare la somma dei prodotti
di ogni valore della variabile per la corrispondente frequenza relativa.
La tecnica di raggruppare le misurazioni che hanno uguali valori prima di calcolarne
la media offre un particolare vantaggio rispetto al metodo standard: essa può essere
applicata a dati che sono stati rappresentati sotto forma di distribuzioni di frequenza.
Per calcolare la media di una distribuzione già suddivisa per intervalli, si deve fare
l’ipotesi che la variabile sia concentrata nel valore centrale dell’intervallo. Pertanto è
necessario determinare i punti centrali delle classi come semisomma degli estremi
dell’intervallo, sostituendo i valori trovati alle classi e procedendo come è stato fatto
per le altre medie.
Esempio: si calcoli la media dell’età di un gruppo di pazienti.
32
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Distribuzione per età di un gruppo di pazienti
Anni (𝑥𝑖 ) 𝑓𝑖 Valore centrale 𝑥𝑖′ 𝑓𝑖 Risultato
(𝑥𝑖′ )
10 – 20 5
15
75
15× 5
20 – 30 7
25
175
25× 7
30 – 40 5
35
175
35× 5
40 – 50 2
45
90
45× 2
50 – 60 3
55
165
55× 3
60 – 70 4
65
260
65× 4
Totale 26
940
In simboli:
∑𝑘1 𝑥𝑖′ 𝑓𝑖
𝑥̅ = 𝑘
∑1 𝑓𝑖
Nel caso dell’esempio precedente si ha:
15 × 5 + 25 × 7 + 35 × 5 + 45 × 2 + 55 × 3 + 65 × 4 940
𝑥̅ =
=
= 36.15
26
26
Quindi la media ponderata è ottenuta pesando ciascun punto medio dell’intervallo per
la frequenza delle osservazioni all’interno dell’intervallo.
Alcune proprietà della media aritmetica.
1. La somma algebrica degli scarti di tutti i termini della media è nulla. (Si
definisce scarto o scostamento la differenza tra ogni termine 𝑥𝑖 della
distribuzione e un qualsiasi valore costante). Questa proprietà può essere
verificata in termini generali. Infatti si ha
𝑛
∑(𝑥𝑖 − 𝑥̅ ) = (𝑥1 − 𝑥̅ ) + (𝑥2 − 𝑥̅ ) + ⋯ + (𝑥𝑁 − 𝑥̅ )
1
= (𝑥1 + 𝑥2 + ⋯ 𝑥𝑁 ) − 𝑛𝑥̅
(𝑥1 + 𝑥2 + ⋯ 𝑥𝑁 )
= (𝑥1 + 𝑥2 + ⋯ 𝑥𝑁 ) − 𝑛
=0
𝑛
Si abbia ad esempio una variabile che assume i seguenti valori 2, 3, 5, 10. La
media aritmetica vale 5, 𝑥̅ = 5. La somma algebrica degli scarti di tali valori
dal valor medio è:
(2 − 5) + (3 − 5) + (5 − 5) + (10 − 5) = −3 − 2 + 5 = 0
33
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
2. La somma dei quadrati degli scarti dalla media aritmetica è un minimo
rispetto alla somma dei quadrati degli scarti da un qualsiasi altro valore diverso
dalla media 𝑥̅ .
Infatti partendo dai dati dell’esempio precedente, la somma dei quadrati degli
scarti dal valor medio risulta
(2 − 5)2 + (3 − 5)2 + (5 − 5)2 + (10 − 5)2 = 38
mentre se prendiamo un valore qualsiasi ad esempio 6 si ha:
(2 − 6)2 + (3 − 6)2 + (5 − 6)2 + (10 − 6)2 = 41
Analogamente se prendiamo il valore 3 si ha:
(2 − 3)2 + (3 − 3)2 + (5 − 3)2 + (10 − 3)2 = 54
Abbiamo verificato questa proprietà per due numeri particolari ma è del tutto
generale. Questa proprietà e molto importante perché mediante i quadrati degli
scarti si definisce una nuova grandezza statistica: la varianza e quindi la media
aritmetica rende minima la varianza.
3. La media aritmetica è associativa. Se una variabile statistica è divisa in 𝑘
gruppi di cui si conoscono le relative medie ̅̅̅,
𝑥1 ̅̅̅,
𝑥2 … . ̅̅̅
𝑥𝑘 e le rispettive
frequenze 𝑓1 , 𝑓2 , … . 𝑓𝑘 , si può ottenere la media della variabile statistica
facendo la media ponderata delle medie dei gruppi
∑𝑘1 𝑥̅𝑖 𝑓𝑖
𝑥̅ = 𝑘
∑1 𝑓𝑖
Ad esempio se l’età media di un gruppo di 15 donne ricoverate in clinica
medica è di 45 anni e quella di 25 maschi ricoverati nella stessa clinica è di 55
anni, l’età media di tutti i ricoverati del reparto è
45 × 15 + 55 × 25
𝑥̅ =
= 51.25
40
Esistono in statistica altri tipi di medie: la media geometrica e la media armonica
La media geometrica
Se 𝑥1 , 𝑥2 , 𝑥3 , … . . , 𝑥𝑁 sono gli 𝑛 valori di una variabile, la media geometrica 𝑀𝑔 di
tali valori è definita dalla radice n-esima del prodotto degli N termini della
distribuzione, ossia in termini matematici:
34
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
𝑛
𝑛
𝑛
𝑀𝑔 = √𝑥1 ∙ 𝑥2 … . 𝑥𝑛 = √∏ 𝑥𝑖
1
ove il simbolo∏𝑛1 𝑥𝑖 indica il prodotto dei termini 𝑥𝑖 quando l’indice 𝑖 varia da 1 a n.
Per le proprietà dei logaritmi diventa
𝑛
1
log 𝑀𝑔 = ∑ log 𝑥𝑖
𝑛
1
cioè il logaritmo della media geometrica è uguale alla media aritmetica dei logaritmi
dei termini. Il calcolo della media geometrica si può fare anche con questa formula.
La media geometrica trova applicazione in quei fenomeni che seguono una legge di
tipo esponenziale, ovvero le cui manifestazioni si verificano in progressione
geometrica. Ad esempio quando si vuol conoscere il tasso di incremento di una
popolazione di batteri la media adeguata è quella geometrica.
Esempio
Il numero di batteri presenti in una popolazione costituita inizialmente da 100
elementi, viene rilevato in periodi successivi: al primo conteggio risultano 112
elementi, al secondo 196 e al terzo 369. Si trovi il tasso d’incremento medio della
popolazione.
Gli incrementi osservati nei tre periodi sono:
112
196
369
= 1.12
= 1.75
= 1.88
100
112
196
Abbiamo quindi questi tre numeri. Per trovare il tasso d’incremento medio, poiché il
fenomeno segue una legge di tipo esponenziale, dobbiamo fare una media geometrica
ossia calcolare
3
𝑀𝑔 = √1.12 × 1.75 × 1.88
Svolgendo tale calcolo si ottiene
𝑀𝑔 = 1.54456
La popolazione ha subito un tasso di incremento medio del 54% ossia la popolazione
ha subito in ogni intervallo un incremento del 54%. Verifica:
100 × (1.54456)3 = 368
Se avessimo calcolato la media aritmetica dei tre numeri precedenti avremmo trovato
1.12 + 1.75 + 1.88
= 1.58333
3
ed è un risultato non corretto. Infatti con questo valore medio il numero di elementi
attesi alla fine dei tre periodi sarebbe stato
100 × (1.58333)3 = 397
La media armonica
35
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
La media armonica 𝑀𝑎 è il reciproco della media aritmetica dei reciproci dei singoli
termini. Se 𝑥1 , 𝑥2 , 𝑥3 , … . . , 𝑥𝑛 sono gli 𝑛 valori di una variabile, la media armonica si
calcola mediante
𝑀𝑎 =
1
1
1
1
+ + ⋯.+
𝑥1 𝑥2
𝑥𝑛
𝑛
=
𝑛
∑𝑛1
1
𝑥𝑖
La media armonica trova applicazione in medicina relativamente a quei fenomeni in
cui occorre ad esempio tenere conto dei tempi di osservazione.
Esempio
Una proteina viene studiata mediante elettroforesi. La proteina viene fatta correre su
gel in un campo elettrico per 20 mm e viene misurato il tempo necessario a
percorrere questa distanza in 5 prove successive. Si vuole conoscere la velocità di
migrazione media.
Si ha
Prova Tempo(s) Velocità(mm/s)
1
40
20/40=0.50
2
60
20/60=0.33
3
30
20/30=0.66
4
50
20/50=0.40
5
70
20/70=0.29
Totale
250
2.186
Abbiamo 5 numeri per trovare il valore medio non dobbiamo fare la media
aritmetica; ossia la velocità media non è la media delle velocità cioè non è
0.5 + 0.33 + 0.66 + 0.40 + 0.29
= 0.4372𝑚𝑚/𝑠
5
Infatti se la velocità media fosse questa, il totale del cammino percorso nelle 5 prove
risulterebbe 0.4372 × 250 = 109.3 𝑚𝑚 mentre il cammino reale nelle 5 prove è
20 × 5 = 100𝑚𝑚.
Per calcolare la media corretta dei 5 numeri dati bisogna tenere presente che si tratta
di una velocità e quindi la velocità media si ottiene dividendo la distanza percorsa
complessivamente per il tempo impiegato a percorrere tale distanza. La distanza
percorsa è 5 volte la stessa distanza 𝑑 (che nel caso in esame vale 20 mm), ed i tempo
totale è la somma dei 5 tempi ossia 𝑡1 + 𝑡2 + ⋯ + 𝑡5 .
36
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
5𝑑
5
=𝑡
𝑡
𝑡
𝑡
𝑡
𝑡1 + 𝑡2 + 𝑡3 + 𝑡4 + 𝑡5
1
+ 2+ 3+ 4+ 5
𝑑 𝑑 𝑑 𝑑 𝑑
5
=
= 𝑀𝑎
1
1
1
1
1
+ + + +
𝑣1 𝑣2 𝑣3 𝑣4 𝑣5
Quindi il valore medio dei 5 numeri è la media armonica ossia:
5
𝑀𝑎 =
= 0.40
1
1
1
1
+
+
+
05 0.33 0.4 0.29
e infatti risulta0.4 × 0.250 = 100𝑚𝑚
𝑉𝑒𝑙𝑜𝑐𝑖𝑡à 𝑚𝑒𝑑𝑖𝑎 =
In conclusione quando si ha una serie di valori 𝑥1 , 𝑥2 , 𝑥3 , … . . , 𝑥𝑁 di una variabile,
prima di decidere quale media fare bisogna tenere presente la natura della variabile.
Tra le tre medie appena esaminate esiste la relazione
𝑀𝑎 ≤ 𝑀𝑔 ≤ 𝑥̅
Il segno di uguale vale quando tutti i valori della variabile statistica sono uguali.
Esaminiamo ora le medie di posizione: la mediana, la moda e i quantili.
Mediana
La mediana è un valore di posizione utilizzabile sia per le variabili quantitative che
per quelle qualitative ordinabili.
La mediana 𝑀𝑒 è un valore medio di posizione ed è il termine che, in una
distribuzione ordinata in ordine crescente o decrescente, occupa il posto centrale
ossia è quel valore/modalità che bipartisce la distribuzione in modo tale da lasciare al
di sotto lo stesso numero di termini che lascia al di sopra. Se n è dispari, la mediana è
esattamente il termine il posto centrale
𝑀𝑒 = 𝑥𝑛+1
2
Esempio. Data la distribuzione 6, 2, 5, 8, 9, si procede a ordinare la distribuzione in
modo ad esempio crescente così da ottenere le seguente graduatoria 2, 5, 6, 8, 9.
Essendo 𝑁 = 5 dispari, applichiamo la formula precedente:
𝑀𝑒 = 𝑥5+1 = 𝑥3 = 6
2
Questo valore è posto proprio nella parte centrale avendo sia a destra che a sinistra un
ugual numero di valori.
Se invece il numero dei termini è pari, la mediana è data per convenzione dalla media
aritmetica dei due termini centrali: 𝑥𝑛 𝑥𝑛+1 . In questo caso si ha
2
2
37
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
𝑀𝑒 =
𝑥𝑛 + 𝑥𝑛+1
2
2
2
Esempio. Data la distribuzione 5, 6, 2, 10, 8, 12 si procede a ordinare i valori in
ordine supponiamo decrescente 12, 10, 8, 6, 5, 2. Essendo 𝑛 = 6 pari, applicando la
formula precedente si ha
𝑥3 + 𝑥4 8 + 6
𝑀𝑒 =
=
=7
2
2
Mediana per dati raccolti in classi
Se si ha una distribuzione con modalità continue divisa in classi, per calcolare la
mediana si individua innanzi tutto la classe mediana con l’aiuto delle frequenze
cumulate e poi si applica l’espressione seguente
𝑛
𝑛
𝑥𝐿 − 𝑥𝑙
𝑐
𝑐
𝑀𝑒 = 𝑥𝑙 + ( − 𝐹𝑖−1
) /𝜑𝑖 = 𝑥𝑙 + ( − 𝐹𝑖−1
)
2
2
𝑓𝑖
ove
 𝑥𝑙 è l’estremo inferiore della classe che contiene la mediana:
 𝑛⁄2 è la posizione centrale della distribuzione
𝑐
 𝐹𝑖−1
è il numero che esprime le frequenze cumulate nella classe antecedente
quella che contiene la mediana
𝑓
 𝜑𝑖 = 𝑖 è la densità di frequenza della classe in cui è contenuta la mediana.
𝑥𝐿 −𝑥𝑙
𝑛
𝑐
Per comprendere questa espressione si tenga presente che ( − 𝐹𝑖−1
)rappresenta
2
l’area della porzione di rettangolo di estremi 𝑥𝑙 ed 𝑀𝑒 (diciamo di un sotto-rettangolo
di estremi 𝑥𝑙 ; 𝑥𝐿 ) perché 𝑛 è l’area sotto l’istogramma e quindi 𝑛⁄2 è l’area della
𝑐
parte di istogramma che si trova a sinistra della mediana mentre 𝐹𝑖−1
è l’area della
parte di istogramma che si trova a sinistra dell’intervallo in cui la mediana. 𝜑𝑖 =
𝑓𝑖
𝑛
𝑐
rappresenta l’altezza del rettangolo di base 𝑀𝑒 − 𝑥𝑙 e quindi ( − 𝐹𝑖−1
) /𝜑𝑖 è il
𝑥𝐿 −𝑥𝑙
2
rapporto tra l’area di un rettangolo e la sua altezza ossia è la base
Esempio. Il perimetro toracico di un gruppo di individui di sesso maschile ha le
misure espresse nella tabella sottostante.
Perimetro toracico frequenza Frequenze cumulate
80 - 86
2
2
86 - 92
10
12
92- 98
20
32
98 – 104
4
36
104 - 110
3
39
Totale
39
38
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
La posizione centrale è
𝑛 39
=
= 19.5
2
2
e di conseguenza le frequenze cumulate in precedenza sono 12 ossia
𝑐
𝐹𝑖−1
= 12
La posizione centrale cade nella frequenza cumulata 32 corrispondente alla classe 92
– 98. Quindi
𝑥𝑙 = 92
Infine l’ampiezza della classe che contiene la mediana è 6 e le frequenze in essa
contenute sono 20
𝑥𝐿 − 𝑥𝑙 = 6
𝑓𝑖 = 20
La mediana risulta quindi:
𝑀𝑒 = 92 + (19.5 − 12)
6
= 92 + 2.25 = 94.25
20
Alcune proprietà della mediana.
a) la mediana, al contrario della media, non è sensibile ai valori estremi;
b) oltre ai dati quantitativi discreti e continui, può essere usata anche per dati
qualitativi ordinali.
c) La mediana rende minima la somma dei valori assoluti degli scarti dei valori
della v.s. dalla mediana:∑|𝑥𝑖 − 𝑀𝑒 | ≤ ∑|𝑥𝑖 − 𝑐| qualunque sia c
Relazioni e confronto tra media e mediana.
La mediana e la media misurano differenti aspetti della posizione di una distribuzione
di frequenze. La mediana è pari all’osservazione centrale di una distribuzione, mentre
la media è il “baricentro”. Possiamo pensare la media come il punto in cui la
distribuzione sarebbe in equilibrio se le osservazioni avessero un peso. La figura
successiva illustra il confronto tra la media e la mediana.
39
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
La relazione tra media e mediana può fornire utili informazioni sulla forma della
distribuzione di frequenza.
Se
𝑚𝑒𝑑𝑖𝑎 = 𝑚𝑒𝑑𝑖𝑎𝑛𝑎
la distribuzione è simmetrica. Le osservazioni equidistanti dalla media (che in questo
caso coincide con la mediana) presentano la stessa frequenza relativa.
Quando non si ha simmetria, cioè la distribuzione è asimmetrica, la media non indica
più dove è localizzata la maggior parte delle osservazioni. In caso di dati asimmetrici
la mediana è spesso la migliore misura di tendenza centrale.
Se
𝑚𝑒𝑑𝑖𝑎𝑛𝑎 < 𝑚𝑒𝑑𝑖𝑎
(ossia la media è a destra della mediana) la distribuzione di frequenza è asimmetrica
(asimmetria positiva) e presenta una coda più lunga a destra rispetto al massimo
centrale. Si dice che la distribuzione è asimmetrica a destra. Quindi in una
distribuzione di frequenze asimmetrica a destra, la media si trova a destra della
mediana
Se
𝑚𝑒𝑑𝑖𝑎 < 𝑚𝑒𝑑𝑖𝑎𝑛𝑎
la distribuzione di frequenza è asimmetrica e, in questo caso, si parla di asimmetria
negativa. La distribuzione presenta una coda più lunga a sinistra rispetto al massimo
centrale. Quindi in una distribuzione di frequenze asimmetrica a sinistra, la media si
trova a sinistra della mediana. La figura precedente mostra una distribuzione di
frequenze asimmetrica a sinistra.
Moda.
40
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
La moda è un altro valore medio di posizione. La moda di una distribuzione è la
modalità della variabile che presenta la massima frequenza. Può essere utilizzata
come misura di sintesi per tutti i tipi di dati, sia quantitativi che qualitativi. Se i dati
sono qualitativi, la modalità con cui si presenta la variabile è formata da
classi/categorie e quindi la moda è la classe che si presenta con maggior frequenza.
Se i dati sono quantitativi, la moda è il valore della variabile che si presenta con
maggior frequenza.
Una distribuzione può avere più di una moda. In tal caso anziché di una distribuzione
unimodale, si parlerà di distribuzione bimodale, trimodale etc.
Esempio1: i valori della variabile quantitativa siano 58,55, 67,55, 59, 53.
La moda della distribuzione è il valore 55
Esempio 2: i valori della variabile siano 57, 58, 59, 62, 63.
In questo caso la moda non esiste
Esempio 3: i valori della variabile siano 56, 55, 58, 58, 63, 68, 67, 68
In questa distribuzione ci sono due valori che si presentano con la frequenza
maggiore 58 e 68 e quindi la distribuzione è bimodale.
Quantili.
I quantili sono quei valori della variabile statistica che dividono la distribuzione di
frequenze in q parti, ognuno delle quali contiene la q –esima parte della distribuzione
complessiva. Possiamo avere i quartili, i decili e i percentili. I quartili sono quei 3
valori che dividono la distribuzione di frequenza in 4 parti . Il primo quartile divide
la distribuzione in due parti: la prima comprende il 25% delle frequenze totali, la
seconda il 75%. Il secondo quartile è la mediana. Il terzo quartile divide la
distribuzione di frequenza in 2 parti: la prima comprende il 75% delle frequenze
totali, la secondo il 25%.
Stesso discorso per i decili e i percentili. Sono valori della variabile statistica che
dividono la distribuzione di frequenza in 10 o in 100 parti e sono rispettivamente 9 o
99. Naturalmente il quinto decile e il 50-esimo percentile coincidono con la mediana.
Per calcolare, ad esempio, i percentili, bisogna disporre le misurazioni in ordine
crescente. Se il numero delle misurazioni è 𝑛, il 25-esimo o il 75- esimo percentile si
ottengono calcolando dapprima
𝑛 × 25
𝑛 × 75
100
100
Tuttavia questi calcoli sono approssimativi, non sono esatti, perché si ottengono
numeri reali e quindi per diminuire questa approssimazione si fa la media fra
l’osservazione corrispondente all’intero e l’osservazione corrispondente all’intero
successivo.
Ad esempio supponiamo di avere le seguenti misurazioni
41
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
2.30 2.15 3.50 2.60 2.75 2.82 4.05 2.25 2.68 3.0
4.02 2.85 3.38
che, messe in ordine crescente, diventano:
2.15 2.25 2.30 2.60 2.68 2.75 2.82 2.85 3.0 3.38 3.50 4.02 4.05
Essendo n=13 si ha
13 × 25
= 3.25
100
che non è intero. L’intero successivo è 4. Quindi il 25 esimo percentile è la media tra
la terza (2.30) e la quarta misurazione (2.60) ossia 2.45.
Analogamente per il 75-esimo percentile si ha
13 × 75
= 9.75
100
che non è intero e quindi il 75-esimo percentile è la media tra la nona e la decima
misurazione ossia 3.19.
Ricapitolando, per i caratteri da noi esaminati possiamo usare i seguenti indici di
posizione:
Carattere
Qualitat. nominale
Qualitat. ordinale
Quantitativo
media
NO
NO
SI
mediana
NO
SI
SI
moda
SI
SI
SI
quartili
NO
SI
SI
Esercizi
Esercizio 1
Calcolare media mediana e moda della variabile statistica:
1
3
11
𝑥𝑖 0
𝑓𝑟 0.10 0.35 0.30 0.25
ove 𝑓𝑟 indica la frequenza relativa.
Si ha
𝑥̅ = 0 × 0.10 + 1 × 0.35 + 3 × 0.30 + 11 × 0.25 = 4
La mediana risulta uguale a 3, e la moda è il valore della variabile che ha frequenza
maggiore ossia 1.
Esercizio 2
42
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Su 50 studenti iscritti al primo anno di una Università italiana nel 2014 sono stati
rilevati i seguenti dati.
X: provenienza territoriale (S=sud, C= centro, N=nord)
Provenienza territoriale N. Iscritti
N
15
C
17
S
18
Z: voto di maturità
Voto di maturità N. Iscritti
60-70
16
70-80
11
80-85
9
85-90
7
90-95
5
95-100
2
W: genere (0=maschio, 1=femmina)
Genere N. iscritti
0
23
1
27
Sintetizzare le variabili statistiche mediante la moda e quando è possibile , la
mediana. Confrontare e commentare i risultati.
Variabile statistica X: provenienza territoriale.
𝑥𝑖
𝑓𝑖
Nord 17
Centro 15
Sud 18
50
𝑓𝑟
0.34
0.30
0.36
1
La modalità più frequente è Sud che raccoglie il 36% della popolazione: tale modalità
non è molto rappresentativa dell’intera popolazione.
La variabile è di tipo qualitativo nominale non ha senso calcolare le frequenze
cumulate e di conseguenza la mediana.
43
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Variabile statistica Y: voto all’esame di maturità.
𝑦𝑙 − 𝑦𝐿
𝑓𝑖 𝐹𝑖𝑐 𝑦𝐿 − 𝑦𝑙
60 − 70 16 16
70 − 80 11 27
80 − 85 9 36
85 − 90 7 43
90 − 95 5 48
95 − 100 2 50
50
10
10
5
5
5
5
𝜑𝑖 =
𝑓𝑖
𝑦𝐿 − 𝑦𝑙
1.6
1.1
1.8
1.4
1
0.4
La variabile si presenta raggruppata in intervalli di ampiezze differenti per cui è
necessario utilizzare le densità di frequenza per individuare la classe modale. Dalla
tabella la classe modale risulta essere (80-85)e ad essa possiamo associare il valore
centrale dell’intervallo e dire che la moda è 𝑦𝑖∗ = 82.5. La moda anche in questo caso
non è molto rappresentativa dell’intera distribuzione.
Essendo la variabile di tipo quantitativo continuo è possibile calcolare la mediana.
Dopo aver individuato l’intervallo (70-80) in cui ricade la mediana, utilizziamo
l’espressione:
𝑛
𝑛
𝑥𝐿 − 𝑥𝑙
𝑐
𝑐
𝑀𝑒 = 𝑥𝑙 + ( − 𝐹𝑖−1
) /𝜑𝑖 = 𝑥𝑙 + ( − 𝐹𝑖−1
)
2
2
𝑓𝑖
Sostituendo i valori numerici si ha:
(25 − 16)
𝑀𝑒 = 70 +
= 78.18
1.1
E’ possibile quindi affermare che almeno il 50% della popolazione assume modalità
minore o uguale a 78.18. La mediana ci dà questa informazione sul fenomeno
statistico X: metà della popolazione ha manifestato un voto non inferiore a 78.18,
un’altra metà un voto non inferiore a 78.18.
Variabile statistica W: genere
Genere
𝑤𝑖
𝑓𝑖 𝑓𝑟
0
maschio 23 0.46
1
femmina 27 0.54
50
La modalità modale in questo caso è Femmina e non è rappresentativa di tutta la
distribuzione in quanto la restante modalità maschio non ha una frequenza molto
dissimile. La variabile W è qualitativa nominale a due modalità (dicotomica) anche
44
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
se è presentata con modalità numeriche, non è possibile attribuirle una mediana in
quanto non esiste un ordinamento fra la modalità maschio e femmina.
Esercizio 3
Il responsabile delle risorse umane di un’azienda deve analizzare 21 candidature per
il posto di assistente del direttore marketing. Dispone delle seguenti tabelle in cui ha
registrato alcuni dati fondamentali dei candidati.
W: titolo di studio (D=Diploma, LT=Laurea Triennale, LM=Laurea Magistrale)
Titolo di studio N. candidati
D
5
LT
10
LM
6
X: età in anni compiuti
Età N. candidati
23
2
24
1
25
3
26
4
27
2
28
3
29
1
30
5
Y: voto di laurea in 110-esimi
Voto di laurea N. candidati
66-90
4
90-95
8
95-100
5
100-105
2
105-110
2
Z: principale lingua straniera (F=francese, I= inglese, S=spagnolo, T=tedesco)
Lingua straniera N. candidati
F
3
I
9
S
4
T
5
45
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Calcolarne la moda, la media e la mediana, quando è possibile.
Variabile statistica W: titolo di studio
𝑤𝑖
Diploma
Laurea Triennale
Laurea Magistrale
𝑓𝑖
5
10
6
21
𝑓𝑟
0.24
0.47
0.29
1
𝐹𝑖𝑐
5
15
21
Si ha
Titolo di studio
Moda
Laurea Triennale
Mediana Laurea triennale
Si può affermare che la modalità Laurea triennale è la più frequente e che almeno il
50% della popolazione possiede titoli di studio inferiori o pari ad esso. Per quanto
riguarda la media non è possibile effettuare il calcolo perché W è una variabile
qualitativa.
Variabile statistica X: Età in anni compiuti
𝑥𝑖
23
24
25
26
27
28
29
30
𝑓𝑖
2
1
3
4
2
3
1
5
21
𝑓𝑟
0.10
0.05
0.14
0.19
0.10
0.14
0.05
0.23
𝐹𝑖𝑐
2
3
6
10
12
15
16
21
Si ha:
Età
Moda
30
Media 27
Mediana 27
46
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
La modalità più frequente di X è 30, ma essa non è molto rappresentativa in quanto
raccoglie solo il 23% della popolazione. IN media o candidati hanno 27 anni e
almeno il 50% di essi al massimo uguaglia questa età.
Variabile statistica Y: voto di laurea in 110-esimi.
𝑦𝑙 − 𝑦𝐿
𝑦𝑖∗
𝑓𝑖 𝐹𝑖𝑐 𝑦𝐿 − 𝑦𝑙
66-90
78
90-95
92.5
95-100 97.5
100-105 102.5
105-110 107.5
4
8
5
2
2
21
4
12
17
19
21
21
24
5
5
5
5
𝑓𝑖
𝑦𝐿 − 𝑦𝑙
0.167
1.6
1
0.4
0.4
𝜑𝑖 =
Per il calcolo della moda bisogna fare riferimento alla densità di frequenze: la classe
con maggiore densità è (90-95) per cui la moda è pari alla modalità centrale 92.5.
Calcolo mediana
La classe in cui cade la mediana è ancora (90-95) per cui, utilizzando l’espressione
𝑛
𝑛
𝑥𝐿 − 𝑥𝑙
𝑐
𝑐
𝑀𝑒 = 𝑥𝑙 + ( − 𝐹𝑖−1
) /𝜑𝑖 = 𝑥𝑙 + ( − 𝐹𝑖−1
)
2
2
𝑓𝑖
e sostituendo i valori numerici si ha:
(10.5 − 4)
𝑀𝑒 = 90 +
= 94.06
1.6
Calcolo media
Poiché i dati sono raggruppati per classi il valore medio è
1
𝑦̅ = ∑ 𝑦𝑖∗ 𝑓𝑖 = ∑ 𝑦𝑖∗ 𝑓𝑟 = 78 × 0.19 + ⋯ + 107.5 × 0.10 = 94.08
𝑛
Poiché i valori ottenuti sono molto prossimi, possiamo affermare che la distribuzione
non presente grandi asimmetrie, ovvero non privilegia né le modalità più basse ne
quelle più alte.
Variabile statistica Z: principale lingua straniera
𝑧𝑖
𝑓𝑖
Francese 3
Inglese 9
Spagnolo 4
Tedesco 5
21
𝑓𝑟
0.14
0.43
0.19
0.24
1
47
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Tutto ciò che è possibile fare su questi dati è trovare la modalità modale, che in
questo caso è inglese e notare che raggruppa il 43% della popolazione, che non è un
valore molto rappresentativo. Essendo una variabile nominale non è possibile
calcolarne la mediana o la media.
Esercizio 4
Vero o falso?
a) Sintetizzare una variabile statistica con un valore medio non produce alcuna
perdita d’informazione
b) Qualunque variabile statistica può essere sintetizzata mediante la moda
c) La mediana ha significato solo per fenomeni almeno ordinali
d) E’ sempre indifferente usare moda mediana e media perché forniscono la
stessa informazione sintetica del fenomeno
e) Se un fenomeno categoriale è codificato in valori numerici (per esempio
0=maschio, 1= femmina) allora è sintetizzabile con la mediana.
f) La media è sempre il miglior valore e quindi è preferibile utilizzarlo in ogni
occasione.
a) F b) V c) V d) F e) F f) F
Esercizio 5
Scegliere la risposta più corretta.
1. La moda di una variabile statistica è:
 La modalità più elevata più elevata o l’intervallo più ampio nel caso di
fenomeni continui.
 Il valore più vicino alla media aritmetica
 La frequenza o la percentuale più elevata
 La modalità a cui è associata la frequenza più elevata o la densità più
elevata nel caso di intervalli.
2. La mediana di una variabile statistica è
 La modalità tale che il 50% delle osservazioni risulta minore di tale
modalità e l’altro 50% risulta maggiore.
 L’osservazione che occupa la posizione centrale della tabella dei dati
grezzi
 La modalità che nell’ordinamento si trova tra la media e la moda.
 La frequenza cumulata relativa pari a 0.5.
3. Per calcolare la media di un fenomeno rilevato in intervalli è necessario
1
 Sostituire le frequenze con le densità 𝑥̅ = ∑ 𝑥𝑖 𝜑𝑖
𝑛
 Sostituire le modalità con il valore centrale degli intervalli 𝑥̅ = ∑ 𝑥𝑖∗ 𝑓𝑖
48
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
1
 Utilizzare l’espressione 𝑥̅ = ∑ 𝑥𝑖 𝑓𝑟
𝑛
4. L’unità di misura in cui è espressa la media è
 Uguale a quella del fenomeno oggetto di studio
 Diversa da quella del fenomeno oggetto di studio
 Quella della mediana elevata al quadrato
 La media non ha unità di misura.
Le risposte corrette sono
1 La moda di una variabile statistica è:
 La modalità a cui è associata la frequenza più elevata o la densità più
elevata nel caso di intervalli.

2 La mediana di una variabile statistica è
 La modalità tale che il 50% delle osservazioni risulta minore di tale
modalità e l’altro 50% risulta maggiore.
3 Per calcolare la media di un fenomeno rilevato in intervalli è necessario
 Sostituire le modalità con il valore centrale degli intervalli 𝑥̅ = ∑ 𝑥𝑖∗ 𝑓𝑖
4 L’unità di misura in cui è espressa la media è
 Uguale a quella del fenomeno oggetto di studio
49
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Variabilità
Esamineremo solo fenomeni quantitativi, sia discreti che continui.
Si è visto che le medie servono per sintetizzare in un solo numero la distribuzione di
una data variabile statistica. Tuttavia nell’analisi di una qualsiasi caratteristica
relativa ad un fenomeno, i valori medi forniscono una sintesi delle osservazioni, ma
non consentono di evidenziare e di valutare eventuali differenze che esistono tra i
valori assunti dalle diverse modalità. Le distribuzioni dei dati possono presentare lo
stesso valore medio ma essere disperse in intervalli di valori molto diversi. Ad
esempio tre individui possono avere i seguenti valori di glicemia.
𝑥1 : 96 98 105 97 95
𝑥2 : 86 100 108 99 98
𝑥3 : 86 125 95 76 109
In tutti e tre i soggetti la glicemia media è 98.2, ma i valori sono dispersi su intervalli
diversi. Il valore medio quindi non fornisce alcuna indicazione sulle variazioni dei
dati e pertanto non è sufficiente a caratterizzare una distribuzione di frequenze.
Come ulteriore esempio, si considerino le due diverse distribuzioni illustrate nella
figura successiva.
50
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Hanno la stessa media, la stessa mediana, la stessa moda. Per sapere di più sulla
distribuzione di frequenze, dobbiamo avere un’idea della variabilità tra i valori dei
dati. Tutte le osservazioni tendono ad essere simili e perciò a situarsi vicino al centro,
o sono distribuite su un ampio intervallo di valori?
Definiamo quindi come “variabilità della distribuzione di frequenze di un fenomeno
quantitativo” l’attitudine del fenomeno quantitativo a manifestarsi con modalità tra
loro diverse e distanti. Così se l’intensità del carattere osservato è la medesima in
tutte le osservazioni effettuate, si dirà che la variabilità è nulla; se, al contrario, sono
molto diverse tra loro , si dirà che la distribuzione presenta una grande variabilità. Si
pone allora il problema di misurare la variabilità. Ciò avviene mediante gli indici di
variabilità.
Gli indici di variabilità si distinguono in indici assoluti e indici relativi. I primi sono
espressi nelle stesse unità di misura usate per i valori del carattere osservato. Sono
indici assoluti il campo di variazione, la differenza interquartile e lo scarto
quadratico medio. Gli indici relativi seno espressi come rapporti fra gli indici assoluti
e altre grandezze omogenee ad essi e perciò sono indipendenti dalle unità di misura e
quindi possono essere utilizzati per confrontare la variabilità di fenomeni diversi
anche quando le intensità dei loro caratteri sono misurate con unità di misura
differenti e quindi non direttamente confrontabili. Un indice di variabilità relativo è il
coefficiente di variazione.
Variabilità assoluta
Campo di variazione (range)
Il campo di variazione di un insieme di 𝑛 termini di una distribuzione è la differenza
tra il valore maggiore e quello minore.
𝑅 = 𝑥𝑚𝑎𝑥 − 𝑥𝑚𝑖𝑛
E’ una misura descrittiva grossolana perché è basata solo su due delle n modalità
osservate, quelle estreme mentre i rimanenti valori della v.s. sono ignorati.
51
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Differenza interquartile
La differenza interquartile (range interquartile) è la differenza tra il terzo quartile
(settantacinquesimo percentile) e il primo quartile (venticinquesimo percentile) e
comprende pertanto il 50% delle osservazioni centrali.
𝑑𝑖𝑓𝑓𝑒𝑟𝑒𝑛𝑧𝑎 𝑖𝑛𝑡𝑒𝑟𝑞𝑢𝑎𝑟𝑡𝑖𝑙𝑒 = 𝑄3 − 𝑄1
oppure
𝑑𝑖𝑓𝑓𝑒𝑟𝑒𝑛𝑧𝑎 𝑖𝑛𝑡𝑒𝑟𝑞𝑢𝑎𝑟𝑡𝑖𝑙𝑒 = 𝑃75 − 𝑃25
Questo indice di variabilità è meno influenzato dai valori estremi rispetto al campo di
variazione. Quando abbiamo definito i percentili ,abbiamo calcolato il 25 esimo e il
75-esimo percentile per una data distribuzione di 13 osservazioni ottenendo i valori
2.45 per il 25–esimo e 3.19 per il 75-esimo percentile.
Pertanto il campo di variazione interquartile è
3.19 − 2.45 = 0.74
Lo scarto quadratico medio, la varianza e la devianza.
Se 𝑥1 , 𝑥2 , … . 𝑥𝑛 sono gli 𝑛 valori di una variabile statistica di valor medio 𝑥̅ , lo
scarto quadratico medio, 𝑠, (detto anche deviazione standard) è la radice quadrata
della media aritmetica dei quadrati degli scarti dei termini dalla loro media. In termini
matematici
∑𝑛1(𝑥𝑖 − 𝑥̅ )2
𝑠=√
𝑛
Il quadrato dello scarto quadratico medio si chiama varianza della distribuzione e il
suo numeratore è la devianza. Pertanto la varianza è
𝑛
(𝑥𝑖 − 𝑥̅ )2
2
𝑠 =∑
𝑛
1
Mentre la devianza si calcola mediante l’espressione
𝑛
∑(𝑥𝑖 − 𝑥̅ )2
1
Esempio:
Si supponga di avere una variabile statistica che assume i seguenti 5 valori
128, 130, 134, 132, 140
Determinare gli scostamenti semplice e quadratico dalla loro media aritmetica e la
varianza.
Cominciamo a calcolare la media aritmetica.
52
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
128 + 130 + 134 + 132 + 140
= 132.8
5
Per calcolare gli scostamenti semplice e quadratico utilizziamo la seguente tabella
𝑥̅ =
𝑥𝑖
𝑥𝑖 − 𝑥̅ (𝑥𝑖 − 𝑥̅ )2
128 −4.8
23.04
130 −2.8
7.84
134
1.2
1.44
132 −0.8
0.64
140
7.2
51.84
Totali
0
84.8
Servendosi di questi risultati si ha:
84.8
𝑠2 =
= 16.96 (𝑣𝑎𝑟𝑖𝑎𝑛𝑧𝑎)
5
𝑠 = √16.96 ≅ 4.12 (𝑠𝑐𝑎𝑟𝑡𝑜 𝑞𝑢𝑎𝑑𝑟𝑎𝑡𝑖𝑐𝑜 𝑚𝑒𝑑𝑖𝑜)
Lo scarto quadratico medio è l’indice di dispersione relativo alla media aritmetica.
Occorre tuttavia notare che in letteratura e in molti pacchetti informatici si considera
al denominatore non n ma (𝑛 − 1). Ci sono argomenti teorici per giustificare questo
cambiamento. C’è comunque da notare che per 𝑛 grande la differenza è irrilevante.
La definizione con 𝑛 al denominatore è chiamata “deviazione standard della
popolazione” mentre quella con 𝑛 − 1 è detta “deviazione standard del campione”.
Se i valori della variabile statistica hanno frequenza 𝑓1 , 𝑓2 , … . 𝑓𝑁 lo scarto quadratico
medio diventa
∑𝑛1(𝑥𝑖 − 𝑥̅ )2 𝑓𝑖
𝑠=√
∑𝑛1 𝑓𝑖
Variabilità relativa
Considereremo solo il coefficiente di variazione dato dal rapporto fra lo scarto
quadratico medio e la media aritmetica.
𝑠
𝐶𝑉 =
𝑥̅
Il coefficiente di variazione è un numero puro in quanto rapporto di due grandezze
omogenee e quindi consente il confronto fra variabili di caratteri eterogenei.
Generalmente viene espressa in percentuale. In pratica si ha:
𝐶𝑜𝑒𝑓𝑓𝑖𝑐𝑖𝑒𝑛𝑡𝑒 𝑑𝑖 𝑣𝑎𝑟𝑖𝑎𝑧𝑖𝑜𝑛𝑒 =
𝑠𝑐𝑎𝑟𝑡𝑜 𝑞𝑢𝑎𝑑𝑟𝑎𝑡𝑖𝑐𝑜 𝑚𝑒𝑑𝑖𝑜
× 100
𝑚𝑒𝑑𝑖𝑎 𝑎𝑟𝑖𝑡𝑚𝑒𝑡𝑖𝑐𝑎
53
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
L’uso di tale indice è necessario quando si vogliono mettere a confronto misure di
variabilità relative a distribuzioni le cui modalità sono espresse in unità di misura
diverse (ad esempio confronto fra aumento di peso e aumento di statura) oppure sono
espresse nella stessa unità di misura ma il loro valore medio risulta molto diverso (ad
esempio spesa per assistito nel 1930 in confronto con la spesa per assistito oggi)
Esempio.
Si vuole confrontare la variabilità della diuresi nelle 24 ore e della pressione in 5
soggetti. Si ha la seguente tabella:
Pressione Sistolica Urine nelle 24 ore
(mm Hg)
(mL)
120
1250
140
1200
160
900
180
850
130
1080
146
1056
𝑥̅
21.5
158.5
𝑠
147.2
150.1
𝑠⁄𝑥̅
Come appare evidente dalla tabella, se ci fossimo fermati ad esaminare il differente
scarto quadratico medio delle due distribuzioni, avremmo affermato una forte
variabilità nelle urine rispetto a quella della pressione perché avremmo commesso il
grande errore di confrontare due fenomeni espressi con due unità di misure diverse
(mm Hg, mL). Viceversa omogeneizzando le due misure a confronto mediante il
calcolo del coefficiente di variazione, risulta che la variabilità dei due fenomeni è
circa uguale.
Esercizi
Esercizio 1
Vero o falso?
a) Il coefficiente di variazione è indispensabile per i confronti di variabilità
b) La devianza è la radice quadrata della varianza.
c) La deviazione standard si chiama così perché è la media di quanto ogni
modalità devia dalla media.
a) V b) F c) V
Esercizio 2
54
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Il range è una misura di variabilità dei valori di una distribuzione, che prende in
considerazione
- solo i valori centrali
- solo i valori estremi
- solo i valori con frequenza maggiore
Il range considera solo i valori estremi
Esercizio 3
Si calcoli la media , la mediana e la differenza interquartile dei seguenti dati.
Si stabilisca infine il tipo di asimmetria della distribuzione.
1.25 1.64 1.91 2.31 2.37 2.38 2.84 2.87 2.93 2.94 2.98 3.00 3.09 3.22 3.41 3.55
Facendo la somma dei 16 dati e dividendo per il loro numero si ottiene
𝑥̅ = 2.605
La mediana si ottiene facendo la media fra l’ottava e la nona osservazione
2.87 + 2.93
𝑀𝑒 =
= 2.90
2
I quartili sono valori che ripartiscono i dati in quattro parti uguali. Il primo quartile (il
25-esimo percentile) è il valore centrale delle misure minori della mediana. Il
secondo quartile è la mediana. Il terzo quartile( il 75-esimo percentile) è il valore
centrale delle misure maggiori della mediana. La differenza interquartile è la
differenza tra il terzo ed il primo interquartile.
𝑑𝑖𝑓𝑓𝑒𝑟𝑒𝑛𝑧𝑎 𝑖𝑛𝑡𝑒𝑟𝑞𝑢𝑎𝑟𝑡𝑖𝑙𝑒 = 𝑄3 − 𝑄1
Tenendo presente che i dati sono 16, il primo interquartile si ottiene con
1 × 16
𝑝𝑟𝑖𝑚𝑜 𝑞𝑢𝑎𝑟𝑡𝑖𝑙𝑒 =
=4
4
Facciamo la media tra il quarto e il quinto valore, ossia
2.31 + 2.37
𝑄1 =
= 2.34
2
Analogamente per il terzo quartile
3 × 16
𝑡𝑒𝑟𝑧𝑜 𝑞𝑢𝑎𝑟𝑡𝑖𝑙𝑒 =
= 12
4
Facciamo la media tra il 12-esimo e il 13-esimo valore ,ossia
3.00 + 3.09
𝑄3 =
= 3.045
2
In conclusione si ha
𝑄3 − 𝑄1 = 3.045 − 2.34 = 0.705
Per determinare il tipo si asimmetria della distribuzione, osserviamo che si è trovato
𝑥̅ = 2.605 e 𝑀𝑒 = 2.90
55
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
ossia
𝑥̅ < 𝑀𝑒
𝑚𝑒𝑑𝑖𝑎 < 𝑚𝑒𝑑𝑖𝑎𝑛𝑎
la distribuzione di frequenza presenta quindi una asimmetria negativa ossia ha una
coda più lunga a sinistra rispetto al massimo centrale.
Esercizio 4
In uno studio che esamina le cause di morte in soggetti affetti da asma grave, sono
stati raccolti dati su 10 pazienti arrivati in ospedale con arresto respiratorio; la
respirazione era assente ed i soggetti erano in stato di incoscienza. La tabella
seguente riporta la frequenza cardiaca dei dieci pazienti al momento dell’ammissione
in ospedale.
Si calcoli la media, la mediana, la moda, la differenza interquartile e la deviazione
standard.
Paziente Frequenza cardiaca
(battiti al minuto)
1
167
2
150
3
125
4
120
5
150
6
150
7
40
8
136
9
120
10
150
𝑥̅ =
167 + 150 + 125 + 120 + 150 + 150 + 40 + 136 + 120 + 150
10
= 130.8 𝐵𝑎𝑡𝑡𝑖𝑡𝑖 𝑎𝑙 𝑚𝑖𝑛𝑢𝑡𝑜
Per calcolare la mediana (o 50-esimo percentile) di una serie di dati bisogna ordinare
le osservazioni dalla più piccola alla più grande. Si ha:
40 120 120 125 136 150 150 150 150 167
56
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Poiché c’è un numero pari di osservazioni, la mediana è data dalla media dei due
valori centrali ossia dalla media fra la quinta e la sesta osservazione. Pertanto la
mediana è
136 + 150
𝑀𝑒 =
= 143 𝑏𝑎𝑡𝑡𝑖𝑡𝑖 𝑎𝑙 𝑚𝑖𝑛𝑢𝑡𝑜
2
La moda di una serie di dati è l’osservazione che si verifica più frequentemente. Il
valore 150 si verifica 4 volte; pertanto è
𝑚𝑜𝑑𝑎 = 150
La differenza interquartile di una serie di dati è la differenza tra il 75-esimo percentile
e il 25-esimo percentile. Essendo 10 le osservazioni si ha
25 × 10
𝑃25 =
= 2.5
100
75 × 10
𝑃75 =
= 7.5
100
Il 25-esimo percentile è la media tra la seconda e la terza misurazione ossia 120
battiti al minuto, mentre il 75-esimo percentile è la media tra la settima e l’ottava
misurazione ossia 150 battiti al minuto.
𝑃75 − 𝑃25 = 150 − 120 = 30 𝑏𝑎𝑡𝑡𝑖𝑡𝑖 𝑎𝑙 𝑚𝑖𝑛𝑢𝑡𝑜
Calcoliamo ora la deviazione standard. Si ha
10
1
𝑠 = ∑(𝑥𝑖 − 130.8)2 = 1258.2 (𝑏𝑎𝑡𝑡𝑖𝑡𝑖 𝑎𝑙 𝑚𝑖𝑛𝑢𝑡𝑜)2
9
2
1
la deviazione standard e la radice quadrata della varianza. Pertanto
𝑠 = √1258.2 = 35.5 𝑏𝑎𝑡𝑡𝑖𝑡𝑖 𝑎𝑙 𝑚𝑖𝑛𝑢𝑡𝑜
La deviazione standard è la misura di dispersione più frequentemente utilizzata. In
genere viene utilizzata con la media per descrivere una serie di valori.
Esercizio 5
Si definisca il coefficiente di variazione, la sua unità di misura e la sua utilità.
Il coefficiente di variazione è definito come il rapporto fra lo scarto quadratico
medio e la media aritmetica.
𝑠
𝐶𝑉 =
𝑥̅
Il coefficiente di variazione è un numero puro in quanto rapporto di due grandezze
omogenee. E’ un parametro utile in quanto consente il confronto fra variabili di
caratteri eterogenei.
Esercizio 6.
Un campione di maschi ha una altezza media di 175.2 cm con una deviazione
standard di 4 cm ed una peso medio di 76 kg con una deviazione standard di 3 kg.
57
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Quale delle due variabili statistiche è più variabile?
Il coefficiente di variazione della prima variabile (la statura) è
𝑠𝑠𝑡𝑎𝑡𝑢𝑟𝑎
4
𝐶𝑉𝑠𝑡𝑎𝑡𝑢𝑟𝑎 =
=
× 100 = 2.28%
𝑥̅𝑠𝑡𝑎𝑡𝑢𝑟𝑎 175.2
Per la seconda variabile, il peso, si ha
𝐶𝑉𝑝𝑒𝑠𝑜 =
𝑠𝑝𝑒𝑠𝑜
3
=
× 100 = 3.9%
𝑥̅𝑝𝑒𝑠𝑜 76
Conclusione: il peso è più variabile.
Esercizio 7
Esempio di calcolo di media e varianza per dati raggruppati.
Calcolo della media e della deviazione standard dei livelli di colesterolo sierico in
soggetti della popolazione maschile degli Stati Uniti di età compresa tra 25 e 34 anni.
I dati sono già stati esaminati e vengono ora riproposti per semplificare il calcolo.
Livello di colesterolo Numero di soggetti
(mg/100mL)
80-119
13
120-159
150
160 -199
442
200-239
299
240-279
115
280-319
34
320-359
9
360-399
5
TOTALE
1067
Per calcolare la media di una serie di dati raggruppati sotto forma di distribuzione di
frequenza, assumiamo che tutti i valori che rientrano in un determinato intervallo
siano uguali al punto medio di quell’intervallo. Così, assumiamo che i 13 valori
all’interno del primo intervallo siano uguali al valore di 99.5 mg/100 mL; tutte le
150 osservazioni comprese nel secondo intervallo – 120-159 mg/100 mL- siano tutte
uguali al valore 139.5 mg/100 mL e così via per tutti gli altri intervalli. Poiché
facciamo queste assunzioni il nostro calcolo è approssimativo. Si ha
𝑥̅ =
99.5 × 13 + 139.5 × 150 + ⋯ + 339.5 × 9 + 379.5 × 5
= 198.8 𝑚𝑔⁄100 𝑚𝐿
1067
58
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Per calcolare la deviazione standard di dati raggruppati, assumiamo, di nuovo, che
tutte le osservazioni che rientrano in un determinato intervallo siano uguali al punto
medio di quell’intervallo. La varianza raggruppata risulta quindi
𝑠2
(99.5 − 198.8)2 × 13 + (139.5 − 198.8)2 × 150 + ⋯ + (279.5 − 198.8)2 × 5
=
1067
= 1929(𝑚𝑔⁄100 𝑚𝐿)2
e quindi la deviazione standard risulta
𝑠 = √1930 = 43.9 𝑚𝑔⁄100 𝑚𝐿
Parte II
Statistica descrittiva bivariata
59
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Tabelle a doppia entrata
In questa parte analizzeremo la rilevazione congiunta di una coppia di fenomeni sulla
stessa popolazione. Il nostro obiettivo diventa la descrizione del comportamento
congiunto dei due fenomeni e l’analisi dell’ eventuale relazione statistica esistente tra
i due fenomeni. La strumentazione statistica che utilizzeremo sarà utile per far
emergere dai dati a disposizione se e come i due fenomeni co-variano e si
influenzano. I due fenomeni X ed Y sono osservati congiuntamente (insieme) su
ciascuna delle unità statistiche che formano la popolazione di interesse. Quindi il
risultato della rilevazione è adesso un insieme di coppie (x,y) che prende il nome di
matrice dei dati grezzi.
Unità statistiche Rilevazione di X Rilevazione di Y
1
…
…
2
…
…
….
x
y
n
…
..
Esempio.
Un collettivo di 15 bambini frequentanti una scuola dell’infanzia è stato sottoposto ad
un test per misurare l’attitudine musicale e l’attitudine al disegno. Il test classifica le
due attitudini secondo la scala sufficiente (S), buona (B), ottima (O). I due fenomeni
sono il risultato del test circa l’attitudine alla musica ( chiamiamolo X) e il risultato
circa l’attitudine al disegno (chiamiamolo Y). Entrambi i fenomeni sono qualitativi
ordinali.
I risultati della rilevazione congiunta sono i seguenti:
Bambino Attitudine alla musica Attitudine al disegno
1
O
O
2
O
B
3
S
B
4
B
B
5
S
S
6
O
S
7
B
O
8
B
O
9
S
B
10
B
B
11
O
O
12
B
S
13
B
B
14
O
S
15
S
B
60
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Per cominciare l’analisi statistica bivariata, il risultato della rilevazione congiunta
viene organizzato in una tabella a doppia entrata composta da righe e colonne.
Y 𝑦1 𝑦𝑗 𝑦ℎ
X
𝑥1
𝑥𝑖
𝑥𝑘
Useremo l’indice i con riferimento al fenomeno X e l’indice j con riferimento al
fenomeno Y. Indicheremo con k ed h il numero di differenti modalità con cui si
manifesta X ed Y rispettivamente. Poniamo sulle righe le k modalità 𝑥𝑖 di X e sulle
colonne le h modalità 𝑦𝑖 di Y. L’interno della tabella si compila contando il numero
dei casi che manifestano la medesima coppia di modalità (𝑥𝑖 , 𝑦𝑖 ). Ai margini della
tbella si pongono le somme dei casi per riga e per colonna. Infine in basso a destra
nell’incrocio, si pone la somma dell’intera tabella.
Ad esempio per i dati grezzi precedenti si ha, contando il numero di bambini che
manifesta le 9 coppie di modalità (S,S), (S, B)…, (O,O) si ha la seguente tabella
composta da k=3 righe e h=3 colonne. Ai margini si hanno le somme dei casi per riga
e per colonna e in basso a destra la somma generale.
Y S B O
X
S
B
O
1
1
2
4
3
3
1
7
0
2
2
4
4
6
5
15
In conclusione la tabella a doppia entrata struttura i dati grezzi bivariati, organizza i
casi osservati.
Frequenze congiunte e marginali
All’interno della tabella si trova la frequenza con cui si manifesta ciascuna coppia di
modalità (𝑥𝑖 , 𝑦𝑖 ). Queste frequenze riguardano entrambi i fenomeni e sono dette
frequenze congiunte che indicheremo con 𝑓𝑖𝑗 cioè utilizzando entrambi gli indici.
Ai margini della tabella si trovano le frequenze che riguardano i fenomeni X ed Y
considerati singolarmente e separatamente. Queste frequenze sono chiamate
61
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
frequenze marginali. Indicheremo con 𝑓𝑖 frequenza marginale di X e con 𝑓𝑗 la
frequenza marginale di Y
Indipendenza statistica.
Si è detto che è di studiare il comportamento congiunto dei due fenomeni, rilevando
l’eventuale relazione fra i due fenomeni. Occorre puntualizzare che considereremo
fenomeni statistici di qualunque natura, cioè sia qualitativi che quantitativi perché
lavoreremo sulle frequenze.
Se fra X ed Y non esiste alcuna relazione statistica allora X ed Y sono statisticamente
indipendenti. Un metodo per stabilire l’esistenza di indipendenza statistica consiste
nel confrontare la tabella osservata con la tabella teorica di indipendenza statistica.
Questa tabella si compila mantenendo fisse le frequenze marginali (che parlano del
comportamento dei singoli fenomeni indipendentemente l’uno dall’altro) e
sostituendo le frequenze congiunte osservate con le frequenze teoriche ( o attese) di
indipendenza statistica 𝑓𝑖𝑗∗ ottenibile con le seguente espressione generale:
𝑓𝑖 𝑓𝑗
𝑓𝑖𝑗∗ =
𝑛
Ad esempio se si ha la seguente tabella osservata riporta dati relativi alle 7058 scuole
secondarie statali e non classificate in base alla tipologia e zona geografica
relativamente all’anno 2013. Quindi X: tipologia; Y: zona geografica.
Y Nord Centro Mezzogiorno
X
Licei
Tecnici
Professionali
𝑓𝑗
1257
909
508
2674
674
376
246
1297
1513
926
648
3087
𝑓𝑖
3444
2211
1403
7058
La tabella delle frequenze attese è quindi
Y
X
Licei
Tecnici
Professionali
𝑓𝑗
Nord
Centro
Mezzogiorno
𝑓𝑖
3444 × 2674
7058
= 1304.7
837.8
531.5
2674
3444 × 1297
7058
= 632.9
406.4
257.8
1297
1506.3
3444
967.2
613.5
3087
2211
1403
7058
62
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Le due tabelle non coincidono cioè le frequenze congiunte osservate non sono tutte
uguali alle frequenze attese . La condizione di indipendenza statistica non è
verificata e quindi X ed Y non sono statisticamente indipendenti: fra tipologia e zona
geografica nelle scuole secondarie superiori italiane c’è qualche relazione
statisticamente rilevabile.
Connessione
Se X ed Y non sono statisticamente indipendenti allora fra i due fenomeni esiste una
relazione statistica. Diremo che X ed Y sono connessi e indicheremo con connessione
una generica relazione statisticamente rilevabile in una coppia di fenomeni osservati
sulla popolazione. La misura di connessione più nota (indice di connessione) ha un
simbolo standard: la lettera greca 𝜒 elevata al quadrato per ricordare che si utilizzano
i quadrati per eliminare l’influenza del segno. Si calcola mediante l’espressione
2
𝑘 ℎ
((𝑓𝑖𝑗 − 𝑓𝑖𝑗∗ ) )
𝜒2 = ∑ ∑
𝑓𝑖𝑗∗
𝑖=1 𝑗=1
Praticamente l’indice di connessione misura quanto la tabella osservata è distante da
quella teorica di indipendenza.
Nell’esercizio precedente avevamo visto che X ed Y non erano indipendenti e quindi
erano connesse. Ora siamo in grado di misurare il grado di connessione. Applicando
la definizione si ha
(1257 − 1304.7)2 (674 − 632.9)2
(648 − 613.5)2
2
𝜒 =
+
+⋯+
= 18.09
1304.7
632.9
613.5
Indice di connessione normalizzato
Ci chiediamo: il valore ottenuto è tanto o è poco? La connessione fra X ed Y è forte o
debole?
Il valore assoluto dell’indice, cioè quello ottenuto mediante l’espressione precedente,
non consente la valutazione, cioè non è interpretabile. Infatti il valore di 𝜒 2 cresce al
crescere di n, della numerosità dei dati ottenuti, perciò in una “grande” popolazione,
il valore di 𝜒 2 è più elevato senza che necessariamente sia più elevata la connessione.
Per rispondere alla nostra domanda serve un altro accorgimento: serve la
normalizzazione. Normalizzare un indice significa trasformarlo in un numero
compreso nell’intervallo (0,1) in modo che , moltiplicato per 100, diventi una
percentuale e quindi facilmente interpretabile. Il valore minimo di 𝜒 2 è 0, mentre il
valore massimo si ottiene moltiplicando la numerosità 𝑛 della popolazione per il più
piccolo tra il numero delle righe (k) e il numero h delle colonne meno 1, ossia
𝑛 × min(𝑘 − 1, ℎ − 1)
La percentuale di connessione permette la valutazione della connessione (tanta o
poca) compatibilmente agli obiettivi di ricerca.
63
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Nel nostro caso:
7058 × min(3 − 1,3 − 1) = 7058 × 2 = 14116
18
= 0.00128 = 0.128%
14116
Associazione (locale) fra coppie di modalità
Consideriamo coppie di fenomeni dicotomici, cioè che assumono ciascuno due sole
modalità. In questo caso la tabella osservata sarà composta da k=2 righe e h=2
colonne ed è chiamata tabella 2x2. Ad esempio su un insieme di studenti ambosessi
vogliamo studiare la propensione al fumo e al consumo di alcol. E si vuol vedere se
statisticamente i fumatori tendono ad essere consumatori di alcol e se i non fumatori
tendono ad essere astemi (o viceversa). In questo caso X: attitudine al fumo, rilevato
con k=2 modalità: famatore/trice (F), non fumatore/trice (NF); Y: consumo di alcol ,
rilevato con h=2 modalità consumatore/trice (C), astemio (A)
Tabella osservata
Y C A
X
F
NF
88 72 160
10 70 80
98 142 240
Ci interessa verificare se esiste un’associazione tra la modalità F di X e C di Y.
Lavoriamo all’interno della tabella lasciando fisse le distribuzioni marginali (che ci
parlano del comportamento monovariato dei due fenomeni, indipendentemente l’uno
dall’altro). Una misura di associazione è l’indice di Yule, definito dall’espressione
𝑓11 𝑓22 − 𝑓12 𝑓21
𝑌𝑢𝑙𝑒 =
𝑓11 𝑓22 + 𝑓12 𝑓21
L’indice Yule può assumere valori che vanno da +1 a −1. Se vale +1 si ha la
massima associazione, −1 si ha la massima repulsione.
Nel caso in esame si ha
88 × 70 − 72 × 10
𝑌𝑢𝑙𝑒 =
= 0.79
88 × 70 + 72 × 10
Questo ci dice che le modalità fumatore/trici e consumatore/trici di alcol tendono ad
associarsi al 79%.
Se X ed Y sono statisticamente indipendenti non esiste associazione in nessuna
coppia di modalità. In caso di indipendenza statistica l’indice di Yule vale 0
qualunque sia la coppia di modalità che mettiamo in posizione (1,1).
64
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Dicotomizzazione della tabella osservata
Per dicotomizzare una tabella kxh, ossia ridurla a dimensione 2x2, si pone in
posizione (1,1) la coppia che interessa e si aggregano le rimanenti modalità in una
unica modalità contraria.
Esempio.
La seguente tabella è tratta da un recente studio riguardo l’atteggiamento di acquisto
di cereali pronti per la colazione.
X: prezzo comparato con la media della categoria rilevato con k=3 modalità inferiore,
uguale o superiore al prezzo medio di categoria.
Y: tipo di regalo /gadget associato al prodotto, rilevato con h=4 modalità.
N=1200 acquirenti di cereali pronti per la colazione presso una catena di
supermercati
Tabella osservata
Y Gadged Raccolta punti Concorso Nessuna
X
≤prezzo medio
= prezzo medio
≥prezzo medio
4
88
280
372
12
113
221
346
2
93
144
239
162
6
75
243
180
300
720
1200
Ci domandiamo se l’assenza di regalo/gadged determina un prezzo inferiore alla
media della categoria. Misuriamo l’associazione nella coppia di modalità”inferiore al
prezzo medio di categoria” di X e “nessun regalo/gadged” di Y. Mettiamo la coppia
che ci interessa in posizione (1,1)e aggreghiamo tutte le altre in un’unica modalità
contraria.
Tabella dicotomizzata
Y Nessuno Regalo/gadget/Concorso
X
≤prezzo medio
≥prezzo medio
𝑌𝑢𝑙𝑒 =
162
81
243
18
939
957
180
1020
1200
162 × 939 − 18 × 81
= 0.981
162 × 939 + 18 × 81
Otteniamo un valore positivo molto vicino a 1 che indica una situazione prossima alla
massima associazione.
65
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Diagramma a dispersione (scatter plot)
Supponiamo di voler descrivere la relazione tra due variabili quantitative continue.
come ad esempio la capacità vitale ( massimo volume di aria che l’organismo può
espirare in seguito ad una inspirazione forzata) e l’altezza. (vedi tabella sottostante)
Altezza CV
Altezza CV
Altezza CV
Altezza CV
(cm)
(Litri)
(cm)
(Litri)
(cm)
(Litri)
(cm)
(Litri)
155.0
2.20
161.2
3.39
166.0
3.66
170.0
3.88
155.0
2.65
162.0
2.88
166.0
3.69
171.0
3.38
155.4
3.06
162.0
2.96
166.6
3.06
171.0
3.75
158.0
2.40
162.0
3.12
167.0
3.48
171.5
2.99
160.0
2.30
163.0
2.72
167.0
3.72
172.0
2.83
160.2
2.63
163.0
2.82
167.0
3.80
172.0
4.47
161.0
2.56
163.0
3.40
167.6
3.06
174.0
4.02
161.0
2.60
164.0
2.90
167.8
3.70
174.2
4.27
161.0
2.80
165.0
3.07
168.0
2.78
176.0
3.77
161.0
2.90
166.0
3.03
168.0
3.63
177.0
3.81
161.0
3.40
166.0
3.50
169.4
2.80
180.6
4.74
Nel caso in cui siano due i caratteri quantitativi si riporta ciascun carattere su ognuno
degli assi ( in genere si pone la variabile dipendente sulle ordinate e la variabile
indipendente sulle ascisse). A questo punto ciascuna unità statistica sul piano è
caratterizzata da una coppia di valori: uno relativo alla modalità del primo carattere,
l’altro alla modalità del secondo carattere.
Capacità vitale (Litri)
5
4,5
4
3,5
3
2,5
2
1,5
1
0,5
0
150
155
160
165
170
175
180
185
Altezza (cm)
66
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Diagramma a dispersione tra capacità vitale ed altezza
L’insieme dei punti apparirà in questi casi come una “nuvola” più o meno addensata
che prende il nome di diagramma a punti o diagramma a dispersione o scatter plot.
Questa rappresentazione viene effettuata al fine di cogliere eventuali proprietà o
legami tra i dati ossia tra le due variabili. Se i punti tendono a distribuirsi nel
diagramma dal basso a sinistra verso l’alto a destra significa che esiste una
associazione positiva tra le due variabili; se viceversa i punti tendono a decorrere
dall’alto a sinistra verso il basso a destra , l’associazione tra le due variabili è
negativa; se è indistinguibile significa che non c’è nessuna associazione tra le due
variabili. Il diagramma a dispersione riesce anche a rivelare se la relazione tra due
variabili possa essere rappresentata da una retta o da una curva più articolata.
Esercizi
Esercizio1
In un’indagine sulla prevenzione del fumo, 20 soggetti sono stati intervistati riguardo
al luogo di residenza in Italia ( Sud=S, Centro=C, Nord=N) e alla propensione al
fumo (Si, No) ottenendo i seguenti risultati:
Fumo
Si No No Si No No Si Si Si Si
Residenza N C C N S S S S N S
Fumo
Si No No Si No No Si Si Si Si
Residenza N C C N S S S S N S
Organizzare i dati in una tabella a doppia entrata. Utilizzando gli stessi dati grezzi,
costruire le due variabili statistiche per i due fenomeni separatamente e verificare che
coincidono con le due distribuzioni marginali della tabella.
La tabella a doppia entrata è la seguente:
Y Centro Nord Sud 𝑓𝑖
X
No
Si
𝑓𝑗
4
0
4
0
6
6
4
6
10
8
12
20
Le due variabili statistiche sono le seguenti:
X 𝑓𝑖
No 8
Si 12
67
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
20
Y
𝑓𝑗
Centro 4
Nord 6
Sud 10
20
Esercizio 2
Vero o falso?
a) In una rilevazione congiunta, due fenomeni vengono osservati su soggetti
diversi e poi riuniti in un’unica tabella di frequenze.
b) La rilevazione congiunta di due fenomeni sulla medesima popolazione
fornisce, come dati grezzi, un elenco di coppie.
c) E’ possibile ricavare le frequenze congiunte dalle frequenze marginali
d) Considerando le sole frequenze marginali si possono costruire variabili
statistiche monovariate.
e) In una tabella a doppia entrata le frequenze congiunte sono bivariate mentre le
frequenze marginali sono monovariate.
a) F b) V c) F d) V e) V
Esercizio 3
Scegliere la risposta più corretta.
1. Una volta organizzati i dati grezzi in una tabella a doppia entrata:
 Non è più possibile analizzare il comportamento di un fenomeno
indipendentemente dall’altro.
 È possibile individuare e studiare l’eventuale relazione statistica
esistente fra i due fenomeni.
 Diventa più difficoltoso analizzare le relazioni statistiche esistenti fra i
due fenomeni
 Non sono più applicabili gli strumenti di statistica descrittiva
monovariata.
2. La variabile statistica doppia
 È costruita dalla somma delle frequenze di due v.s. semplici
 E data dall’accostamento delle frequenze di due v.s. semplici
 Si legge all’interno della tabella a doppia entrata
 È costituita dal prodotto di due v.s.
68
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Le risposte corrette sono:
Una volta organizzati i dati grezzi in una tabella a doppia entrata:
 È possibile individuare e studiare l’eventuale relazione statistica
esistente fra i due fenomeni.
La variabile statistica doppia
 Si legge all’interno della tabella a doppia entrata
Esercizio 4
Il proprietario di un negozio ritiene che sia possibile mettere in relazione il fenomeno
“taccheggio” con l’”età dei propri clienti” e che la propensione al taccheggio aumenti
con l’età. Per un’intera settimana intensifica i controlli e classifica i propri clienti
secondo l’età (≤30 anni, fra 30 e 60 anni, ≥60 anni) e a seconda che siano sorpresi o
meno a taccheggiare (Si,No) ottenendo
≤ 30 30 − 60 ≥ 60
Si
10
1
3
14
No 65
36
23 124
75
37
26 138
Valutare il grado di connessione (globale) fra i due fenomeni nel collettivo osservato.
Per valutare il grado di connessione esistente è necessario introdurre un indicatore
appropriato. L’indice che segnala la presenza di un generico legame tra due variabili
è l’indice di connessione 𝜒 2 . La tabella teorica di indipendenza è:
≤ 30
30 − 60 ≥ 60
14
×
75
Si
3.75
2.64 14
= 7.61
138
No
67.39
33.25 23.36 124
75
37
26 138
E, utilizzando la definizione:
2
𝑘 ℎ
((𝑓𝑖𝑗 − 𝑓𝑖𝑗∗ ) )
𝜒2 = ∑ ∑
𝑓𝑖𝑗∗
𝑖=1 𝑗=1
si ottiene:
(10 − 7.61)2
(23 − 23.36)2
𝜒 =
+ ⋯+
= 3.13
7.61
23.36
2
𝜒 2 diverso da zero indica che fra i due fenomeni esiste un generico legame, ma
questo indice non permette di valutare il grado di connessione tra i due fenomeni.
Bisogna calcolare il 𝜒 2 normalizzato che vale:
69
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
𝜒2
3.13
=
= 0.02
𝑛 × min(𝑘 − 1, ℎ − 1) 138 × min(2 − 1,3 − 1)
Questo valore indica che vi è il 2% della connessione massima ossia un bassissimo
grado di connessione.
Esercizio 5
Vero o falso?
a) Quando la relazione tra due fenomeni è molto debole, si dice che i due
fenomeni sono statisticamente indipendenti.
b) La connessione è una generica relazione tra due fenomeni
c) La normalizzazione dell’indice 𝜒 2 è necessaria per la valutazione del grado di
connessione.
d) L’indice di Yule misura in percentuale il grado di associazione o repulsione fra
due modalità.
e) L’analisi di associazione (locale) è effettuabile solo su tabelle dicotomiche o
dicotomizzate.
a) V b) V c) V d) V e) V
70
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Parte III
Statistica inferenziale
Finora l’obiettivo era la descrizione del comportamento del fenomeno X o della
coppia di fenomeni X e Y su dati rilevati. In ogni caso si dispone sempre di dati
parziali cioè relativi a una parte dell’intera popolazione ossia ad un campione di
numerosità 𝑛 perché il collettivo è infinito o molto grande. L’obiettivo ora è di
estendere l’analisi del comportamento di X all’intera popolazione. Si tratta di inferire
dal campione all’intera popolazione. I metodi statistici adeguati a questo scopo
costituiscono la statistica inferenziale. Passeremo dunque dalla descrizione
all’inferenza.
Per fare buona inferenza è strategico che il campione abbia la caratteristica della
rappresentatività cioè sia un’immagine su scala ridotta della popolazione da cui è
stato estratto. L’inferenza statistica si basa su campioni casuali. Un campione è
casuale quando è scelto a caso dalla popolazione, ossia selezionato senza criteri o
sistematicità. La casualità di un campione è garanzia della sua rappresentatività.
Lo strumento scientifico per trattare il caso e i suoi effetti è la teoria della
probabilità. L’inferenza statistica avviene su base probabilistica. Per introdurre gli
strumenti di inferenza statistica abbiamo bisogno di imparare qualche elemento della
teoria della probabilità.
Elementi di calcolo delle probabilità
Probabilità di un evento aleatorio
Un evento aleatorio è un avvenimento che può verificarsi secondo diverse modalità
che chiameremo eventi elementari e non possiamo prevedere a priori quale modalità,
quale evento elementare si verificherà perché il verificarsi di un qualunque evento
elementare è soggetto solo alla legge del caso. Esempi sono il lancio di un dado o di
una moneta. Tuttavia, per quanto il verificarsi di un evento aleatorio non possa
essere previsto con certezza, possiamo valutarne la probabilità. Si definisce
71
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
probabilità di un evento aleatorio il rapporto tra il numero dei casi favorevoli
(numero dei casi in cui si manifesta l’evento elementare) e il numero dei casi
possibili cioè il numero totale degli eventi elementari. Ad esempio se consideriamo
l’evento lancio di una moneta allora la probabilità che si verifichi, ad esempio, testa è
1⁄2 perché abbiamo un caso favorevole (l’evento elementare testa) e due casi
possibili (gli eventi elementari testa e croce). Se l’evento è il lancio di un dado allora
la probabilità che si verifichi un punteggio qualunque, ad esempio 5, è 1⁄6 perché gli
eventi elementari complessivi sono 6 e l’evento elementare favorevole è 1.
La probabilità così definita viene chiamata probabilità matematica. Possiamo
calcolarla solo se si conoscono a priori i casi favorevoli e quelli possibili. In molti
casi pratici questa situazione non si verifica. Ad esempio per la medicina è il calcolo
della probabilità che un individuo contragga una certa malattia. In queste situazioni si
dà la definizione di probabilità statistica. Si effettua un grande numero 𝑛 di
osservazioni e si rivela il numero 𝑚 di volte (ossia la frequenza) in cui la modalità
dell’evento si verifica. Si considera quindi la frequenza relativa dell’evento
𝑚
𝑓𝑟 =
𝑛
L’esperienza mostra che tali valori al crescere delle osservazioni tendono a un valore
che viene chiamato probabilità statistica dell’evento. Si è visto che nei casi in cui è
possibile determinare tanto la probabilità matematica che quella statistica di uno
stesso evento, i due valori sono uguali e quindi ammettiamo la legge empirica del
caso: il valore della frequenza relativa di un evento rilevato su un grande numero di
prove effettuate nelle stesse condizioni, tende a quello della probabilità matematica e
l’approssimazione cresce al crescere delle prove.
Principi fondamentali del calcolo delle probabilità
Principio delle probabilità totali.
Per probabilità totale di due eventi casuali A e B s’intende la probabilità che si
verifichi l’evento A oppure l’evento B. Tale probabilità si calcola in modo diverso a
seconda che i due eventi siano compatibili o incompatibili.
Due eventi casuali A e B sono incompatibili quando non possono verificarsi
contemporaneamente ossia quando gli eventi elementari che compongono l’evento
casuale A non hanno nessun elemento comune agli eventi elementari dell’evento B.
Se indichiamo con P(A) e P(B) le rispettive probabilità, la probabilità totale P(A+B)
degli eventi A e B è data dalla somma delle probabilità di ciascuno dei due eventi:
(regola della somma)
𝑃(𝐴 + 𝐵) = 𝑃(𝐴) + 𝑃(𝐵)
Se due eventi sono incompatibili e vogliamo conoscere la probabilità che si verifichi
l’uno oppure l’altro, dobbiamo usare la regola della somma.
72
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Esempio. Si abbia un’urna contenente 100 palline, tutte uguali nella forma ma di
colore differente; 10 sono bianche, 40 rosse e le rimanenti 50 nere. Vogliamo
calcolare la probabilità che facendo una sola estrazione si ottenga una pallina bianca
(evento A) oppure una pallina nera (evento B). I due eventi sono incompatibili, si
escludono a vicenda.
La probabilità di estrarre una pallina bianca è P(A)=10/100 mentre la probabilità di
estrarre una pallina nera è P(B)=50/100; dunque la probabilità totale è
10
50
60
𝑃(𝐴 + 𝐵) =
+
=
= 0.6
100 100 100
La regola della somma può essere estesa a più di due eventi purché siano tutti
incompatibili. Per esempio supponiamo di voler conoscere la probabilità di ottenere il
punteggio 3 o più di 3 con un singolo lancio di un dado. 3 o più di 3 comprende i
seguenti quattro risultati 3 (evento A) oppure 4 (evento B)oppure 5 (evento C) oppure
6 (evento D). Questi quattro possibili risultati sono incompatibili fra loro perché non
possiamo ottenere ad esempio 4 e 5 contemporaneamente con lo stesso dado.
Possiamo dunque calcolare la probabilità di ottenere 3 o un punteggio maggiore di 3
usando la regola della somma
1 1 1 1 4 2
𝑃(𝐴 + 𝐵 + 𝐶 + 𝐷) = 𝑃(3) + 𝑃(4) + 𝑃(5) + 𝑃(6) = + + + = =
6 6 6 6 6 3
Se gli eventi A e B sono compatibili, ossia si possono verificare
contemporaneamente, o, se si preferisce, gli eventi elementari di A hanno elementi
comuni agli eventi elementari dell’evento B, per calcolare la probabilità totale si
applica la seguente regola detta regola della somma generalizzata :
𝑃(𝐴 + 𝐵) = 𝑃(𝐴) + 𝑃(𝐵) − 𝑃(𝐴𝐵)
ove 𝑃(𝐴𝐵) sta ad indicare la probabilità che l’evento A e l’evento B si verifichino
contemporaneamente ovvero la probabilità che si verifichino gli eventi elementari
comuni ai due eventi. Se non si fa questa sottrazione, i risultati in cui gli eventi A e B
si verificano contemporaneamente vengono contati due volte. Naturalmente, se A e B
sono incompatibili, non hanno elementi comuni e quindi 𝑃(𝐴𝐵) = 0
Esempio. Calcolare la probabilità che facendo una sola estrazione da un mazzo di 40
carte si ottenga una carta di picche oppure una figura. Si ha
10
12
𝑃(𝐴) =
𝑃(𝐵) =
40
40
perché le picche sono 10 e le figure sono 12. Tuttavia in questo modo le 3 figure di
picche vengono contate due volte. La probabilità di estrarre una figura di picche da
un mazzo di 40 carte è
3
𝑃(𝐴𝐵) =
40
In conclusione per gli eventi compatibili
10 12 3
19
𝑃(𝐴 + 𝐵) =
+
−
=
40 40 40 40
73
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Allo stesso risultato si perviene applicando per il calcolo di 𝑃(𝐴𝐵)il principio delle
probabilità composte che verrà analizzato successivamente.
Altro esempio. Si consideri un’urna contenente 6 palline uguali fra loro e numerate
da 1 a 6. Vogliamo calcolare la probabilità che eseguendo una sola estrazione si abbia
una pallina che sia dispari oppure che abbia un numero non superiore a 4 Indichiamo
con A l’evento aleatorio “estrazione di una pallina con numero dispari”. L’evento A
comprende quindi i seguenti tre eventi elementari “estrazione di una pallina con
numero 1”, estrazione di una pallina con numero 3” infine “estrazione di una pallina
con numero 5”. A(1,3,5) Indichiamo con B l’evento estrazione di una pallina con
numeri compresi da 1 a 4 L’evento B comprende gli eventi elementari “estrazione di
una pallina con numero 1”……..”estrazione di una pallina con numero 4” :
B(1,2,3,4). E’:
3 1
4 2
𝑃(𝐴) = =
𝑃(𝐵) = =
6 2
6 3
Gli eventi A e B hanno comuni i seguenti due eventi elementari: “estrazione di una
pallina con numero 1” “estrazione di una pallina con numero 3”, e, di conseguenza
2 1
𝑃(𝐴𝐵) = =
6 3
Applicando la formula generale si ha
𝑃(𝐴 + 𝐵) =
1 2 1 5
+ − =
2 3 3 6
Probabilità condizionata e principio della probabilità composta
Si abbiano due eventi casuali A e B e si voglia determinare la probabilità 𝑃(𝐴𝐵) che
si verifichino entrambi gli eventi. Il verificarsi del primo evento a volte modifica la
probabilità del verificarsi dell’altro evento ed a volte la lascia inalterata. Nel primo
caso i due eventi sono dipendenti nel secondo sono indipendenti.
Si abbia, ad esempio, un’urna contenente 7 palline bianche e 3 palline nere. La prova
consiste nell’estrarre due palline, una di seguito all’altra senza rimettere la prima
pallina nell’urna. In questo caso il verificarsi del primo evento modifica la probabilità
del secondo evento e quindi gli eventi sono dipendenti. Calcoliamo la probabilità
P(AB) che la prima pallina estratta sia bianca e la seconda sia nera; è importante
l’ordine. Sia A l’evento “la prima pallina estratta è bianca”. Si ha
7
𝑃(𝐴) =
10
Indichiamo con B l’evento “la seconda pallina estratta è nera” e con 𝑃(𝐵/𝐴) la
probabilità di estrarre una pallina nera senza aver rimesso la pallina estratta
nell’urna. 𝑃(𝐵/𝐴) è la probabilità di B condizionata ad A, ossia è la probabilità del
verificarsi di B nell’ipotesi che A si sia verificato. Tale probabilità sarà
74
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
3 1
=
9 3
Il principio dell’evento composto afferma che la probabilità che accadano due eventi
è uguale al prodotto delle probabilità di un evento per la probabilità del verificarsi
dell’altro condizionata al verificarsi del primo. In termini matematici possiamo
scrivere
𝑃(𝐵/𝐴) =
𝑃(𝐴𝐵) = 𝑃(𝐴) × 𝑃(𝐵⁄𝐴)
Nel caso appena esaminato si ha quindi:
7 1
7
𝑃(𝐴𝐵) =
× =
= 0.233
10 3 30
Vogliamo ora trovare la probabilità che estraendo due palline la prima sia bianca e la
seconda nera ma nell’ipotesi che dopo aver estratto la prima pallina questa venga
rimessa nell’urna in modo da ricreare le condizioni di partenza. Indichiamo sempre
con A l’evento “la prima pallina è bianca” e con B l’evento “la seconda pallina è
nera”. In questo caso gli eventi sono indipendenti e la probabilità di B condizionata
ad A è la probabilità che si verifichi l’evento B; ossia si ha
3
𝑃(𝐵/𝐴) = 𝑃(𝐵) =
10
Il principio della probabilità composta nel caso di eventi indipendenti diventa
𝑃(𝐴𝐵) = 𝑃(𝐴) × 𝑃(𝐵)
ossia è uguale al prodotto delle probabilità.
Nel caso in esame si ha quindi:
7
3
21
𝑃(𝐴𝐵) =
×
=
= 0.210
10 10 100
Distribuzioni teoriche di probabilità
La variabile aleatoria (casuale)
Qualsiasi caratteristica che può essere misurata o categorizzata è detta variabile. Se
una variabile può assumere numerosi valori tali che qualsiasi risultato è determinato
dal caso, essa è nota come variabile casuale. Si sono già visti esempi di variabili
casuali. Le variabili casuali sono di solito rappresentate da lettere maiuscole quali X,
Y e Z. Una variabile casuale discreta può assumere solo un numero finito o
numerabile di risultati. Una variabile casuale continua può assumere qualsiasi valore
75
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
nell’ambito di uno specifico intervallo. Nella teoria della probabilità le variabili
casuali sono chiamate variabili aleatorie perché stanno ad indicare un rischio
calcolato, ma i due termini casuale ed aleatorio vengono usati indifferentemente.
Distribuzioni di probabilità discrete
Una variabile aleatoria (v.a.) X discreta è una quantità variabile che può assumere i
valori 𝑥1 , 𝑥2 , … 𝑥𝑛 al verificarsi degli eventi 𝐸1 , 𝐸2 … 𝐸3 con probabilità
rispettivamente 𝑝1 , 𝑝2 , … . 𝑝𝑛 tali che la loro somma sia 1, cioè
𝑛
∑ 𝑝𝑖 = 𝑝1 + 𝑝2 + ⋯ + 𝑝𝑛 = 1
1
L’insieme dei valori di una v.a. X con le rispettive probabilità p(X) viene chiamato
distribuzione di probabilità discreta.
Valore medio e varianza di una variabile statistica discreta
Data una qualunque v.a. X che assume i valori 𝑥1 , 𝑥2 , … 𝑥𝑛 con probabilità
rispettivamente 𝑝1 , 𝑝2 , … . 𝑝𝑛 si dice valore medio 𝜇, la somma dei valori 𝑥1 , 𝑥2 , … 𝑥𝑛
moltiplicati per le rispettive probabilità 𝑝1 , 𝑝2 , … . 𝑝𝑛 ; ossia
𝜇 = 𝑥1 𝑝1 + 𝑥2 𝑝2 + ⋯ . . +𝑥𝑛 𝑝𝑛
Il valore medio è quindi una media pesata sulle probabilità.
La varianza di una qualunque v.a. discreta X che assume i valori 𝑥1 , 𝑥2 , … 𝑥𝑛 con
probabilità rispettivamente 𝑝1 , 𝑝2 , … . 𝑝𝑛 e avente valore medio 𝜇, è definita come
𝜎 2 = ∑(𝑥𝑖 − 𝜇)2 𝑝𝑖 = (𝑥1 − 𝜇)2 𝑝1 + (𝑥2 − 𝜇)2 𝑝2 + ⋯ + (𝑥𝑛 − 𝜇)2 𝑝𝑛
Esempi di distribuzioni di probabilità discrete
Esempi di variabili aleatorie discrete sono: il risultato del lancio di un dado oppure
lancio di una moneta.
Nel caso dell’evento “lancio di un dado” la distribuzione di probabilità è:
X
1
2
3
4
5
6
p(X) 1/6 1/6 1/6 1/6 1/6 1/6
perché l’ evento può presentarsi con modalità 1, 2, 3, 4, 5, 6 ciascuna delle quali ha
probabilità 1⁄6; mentre nel caso dell’evento “lancio di una moneta” la distribuzione
di probabilità è
X
T C
p(X) 1/2 1/2
perché l’evento può presentarsi secondo due modalità T e C ciascuna con probabilità
1⁄2.
76
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Per ogni distribuzione di probabilità la somma di tutte le probabilità dà la certezza
cioè 1. Così:
1 1 1 1 1 1
𝑝= + + + + + =1
6 6 6 6 6 6
Utilizzando i principi fondamentali del calcolo delle probabilità si possono calcolare
le distribuzioni di probabilità di un qualunque evento aleatorio. Calcoliamo come
esempio la distribuzione di probabilità della variabile aleatoria “somma del punteggio
di due dadi”. Per ottenere il punteggio 2 deve verificarsi il seguente evento composto
“ punteggio 1 sul primo dado e punteggio 1 sul secondo” (lo chiameremo evento A).
Ciascuno dei due eventi elementari ha probabilità 1⁄6; inoltre sono indipendenti
perché il verificarsi del primo evento non altera la probabilità di verificarsi del
secondo. Di conseguenza la probabilità che si verifichi l’evento A è il prodotto delle
due probabilità ossia 1⁄36.
1
𝑃(𝐴) =
36
Il punteggio 3 può essere ottenuto mediante il seguente evento composto: “punteggio
2 sul primo dado e punteggio 1 sul secondo” ( lo chiameremo evento B). Ripetendo il
ragionamento precedente si ottiene che la probabilità che si verifichi l’evento B è
1⁄36.
1
𝑃(𝐵) =
36
Il punteggio 3 può essere ottenuto anche mediante un altro evento composto:
“punteggio 1 sul primo dado e punteggio 2 sul secondo dado” (lo chiameremo evento
C). L’evento B e l’evento C sono incompatibili perché non possono verificarsi
simultaneamente, quindi la probabilità che si verifichi o l’uno o l’altro è la somma
delle due probabilità
2
𝑃(2) = 𝑃(𝐴) + 𝑃(𝐵) =
36
Ripetendo simili ragionamenti per tutti gli altri punteggi si ottiene la seguente
distribuzione di probabilità
X
2
3
4
5
6
7
8
9
10
11
12
p(X) 1/36 2/36 3/36 4/36 5/36 6/36 5/36 4/36 3/36 2/36 1/36
Distribuzione binomiale
E’ la più importante distribuzione teorica di probabilità discreta.
77
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Supponiamo di lanciare una moneta due volte e di voler determinare la distribuzione
di probabilità del numero di teste. I casi possibili sono in tutto 22 = 4 e sono i
seguenti
TT; TC; CT; CC
Quindi la distribuzione di probabilità dell’evento X “numero di teste in due lanci” è
la seguente:
X
0
1
2
p(X) 1/4 1/2 1/4
Supponiamo ora di lanciare la moneta 3 volte. Il numero di combinazioni possibili
per gli esiti generati dai 3 lanci sono 23 = 8 così distribuiti
TTT; TTC; TCT; CTT; CCT; CTC; TCC, CCC
La distribuzione di probabilità dell’evento X “numero di teste in tre lanci” è la
seguente:
X
0
1
2
3
p(X) 1/8 3/8 3/8 1/8
Siamo quindi in grado di calcolare la distribuzione di probabilità per un numero
qualunque di lanci ma diventerebbe molto complicato elencare tutti gli esiti possibili
per esempio per 10 lanci (210 = 1024). Seguire questa strada non è molto
conveniente. Esiste invece un’espressione che ci permette di determinare la
distribuzione di probabilità in tutte quelle situazioni in cui un evento può presentarsi
secondo due modalità. Proprio perché le possibilità sono due, tale distribuzione viene
chiamata distribuzione binomiale
E’ la più importante distribuzione di probabilità per una variabile discreta. Descrive
la seguente situazione generale. Consideriamo un evento che può presentarsi secondo
due modalità: una la chiameremo successo, l’altra insuccesso. Supponiamo di fare 𝑛
prove indipendenti ognuna delle quali dà luogo ad uno dei due eventi mutuamente
esclusivi, e in ogni prova l’evento abbia una probabilità costante 𝑝 di verificarsi. I
valori del numero delle prove 𝑛 e della probabilità 𝑝 costante di verificarsi
dell’evento caratterizzano la distribuzione binomiale nel senso che noti questi due
valori è completamente determinata la distribuzione di probabilità binomiale.
Vogliamo calcolare la probabilità che l’evento considerato si verifichi 𝑘 volte nelle 𝑛
prove considerate ossia si verifichino 𝑘 successi. Si può dimostrare che tale
probabilità si calcola mediante la seguente espressione
𝑛!
𝑃(𝑛, 𝑘) =
𝑝𝑘 𝑞 𝑛−𝑘
𝑘! (𝑛 − 𝑘)!
ove 𝑞 = 1 − 𝑝 è la probabilità di insuccesso.
Esempio 1.
78
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Supponiamo di lanciare 4 volte una moneta. Calcoliamo la distribuzione di
probabilità del numero di teste, ossia la probabilità di ottenere 𝑘 = 0,1,2,3,4 volte
testa.
Si ha
4! 1 0 1 4
1 4
𝑘=0
𝑃(4,0) =
( ) ( ) = ( ) = 0.063 = 6.3%
0! 4! 2
2
2
𝑘=1
4! 1 1 1 3
1 4
𝑃(4,1) =
( ) ( ) = 4 ( ) = 0.25 = 25%
1! 3! 2
2
2
𝑘=2
4! 1 2 1 2
1 4
𝑃(4,2) =
( ) ( ) = 6 ( ) = 0.38 = 38%
2! 2! 2
2
2
𝑘=3
4! 1 3 1 1
1 4
𝑃(4,3) =
( ) ( ) = 4 ( ) = 0.25 = 25%
3! 1! 2
2
2
𝑘=4
4! 1 4 1 0
1 4
𝑃(4,4) =
( ) ( ) = ( ) = 0.063 = 6.3%
4! 0! 2
2
2
Esempio 2.
Calcolare la distribuzione di probabilità relativa all’evento “numero di volte in cui si
presenta il punteggio 3 lanciando un dado 4 volte”. Anche in questo caso siamo di
fronte ad una variabile discreta che si presenta con due modalità: punteggio 3
(successo) punteggio diverso da 3 (insuccesso). La probabilità 𝑝 (successo) di
ottenere il punteggio 3 è 1⁄6 mentre la probabilità di insuccesso 𝑞 = 1 − 𝑝 è 5⁄6.
4! 1 0 5 4
𝑘=0
𝑃(4,0) =
( ) ( ) = 0.4822
0! 4! 6
6
𝑘=1
4! 1 1 5 3
𝑃(4,1) =
( ) ( ) = 0.3858
1! 3! 6
6
𝑘=2
4! 1 2 5 2
𝑃(4,2) =
( ) ( ) = 0.1157
2! 2! 6
6
𝑘=3
4! 1 3 5 1
𝑃(4,3) =
( ) ( ) = 0.0154
3! 1! 6
6
𝑘=4
4! 1 4 5 0
𝑃(4,4) =
( ) ( ) = 0.0008
4! 0! 6
6
79
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Valore medio e varianza
Per ottenere il valor medio di successi 𝜇 in 𝑛 prove, se 𝑝 è la probabilità di successo
costante in ogni prova, dobbiamo sommare i possibili valori che la variabile aleatoria
può assumere - ossia il numero di successi attesi in una serie di 𝑛 prove - per le
rispettive probabilità. Indicato con 𝑘𝑖 il numero di successi nella i-esima prova (ossia
i valori 0,1,2,…𝑛 che la variabile casuale può assumere) e con 𝑃(𝑛, 𝑘𝑖 ) la probabilità
che in 𝑛 prove si verifichino 𝑘𝑖 successi, il valor medio 𝜇 di una variabile che segue
la distribuzione binomiale è
𝑛
𝜇 = ∑ 𝑘𝑖 ∙ 𝑃(𝑛, 𝑘𝑖 ) = 𝑘1 ∙ 𝑃(𝑛, 1) + 𝑘2 ∙ 𝑃(𝑛, 2) + ⋯ + 𝑘𝑛 ∙ 𝑃(𝑛, 𝑛)
𝑖=1
Si può dimostrare che tale espressione è uguale al prodotto delle prove 𝑛 per la
probabilità di successo in ogni prova, ossia
𝑛
𝜇 = ∑ 𝑘𝑖 ∙ 𝑃(𝑛, 𝑘𝑖 ) = 𝑛𝑝
𝐾=1
Non dimostreremo questa espressione ma la verificheremo nel caso particolare del
lancio di una moneta per 4 volte ossia calcoliamo il numero medio di teste atteso
lanciando una moneta 4 volte. Tenendo presente i calcoli precedentemente svolti si
ha
4
1 4
1 4
1 4
1 4
1 4
𝜇 = ∑ 𝑘𝑖 ∙ 𝑃(𝑛, 𝑘𝑖 ) = 0 ∙ ( ) + 1 ∙ 4 ( ) + 2 ∙ 6 ( ) + 3 ∙ 4 ( ) + 4 ∙ ( )
2
2
2
2
2
𝑖=1
1 4
= 32 ( ) = 2
2
D’altra parte, se si calcola il valore medio mediante il prodotto delle prove 𝑛 per la
probabilità di successo in ogni prova si ha:
1
𝜇 = 𝑛𝑝 = 4 = 2
2
Il valore medio rappresenta il valore atteso perché ci si aspetta che in 4 lanci di una
moneta il valore medio dei successi sia 2.
La distribuzione binomiale, come tutte le distribuzioni, oltre ad un valore medio ha
una deviazione standard.
Applicando la definizione di varianza di una qualunque distribuzione discreta alla
generica distribuzione binomiale relativa ad 𝑛 prove con probabilità di successo 𝑝
costante in ogni prova risulta si ha
80
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
𝜎 2 = ∑(𝑘𝑖 − 𝜇)2 𝑃(𝑛, 𝑘𝑖 )
= (𝑘1 − 𝜇)2 𝑃(𝑛, 𝑘1 ) + (𝑘2 − 𝜇)2 𝑃(𝑛, 𝑘2 ) + ⋯ + (𝑘𝑛 − 𝜇)2 𝑃(𝑛, 𝑘𝑛 )
Si può dimostrare che questa espressione è equivalente a
𝜎 2 = 𝑛𝑝𝑞
ossia la deviazione standard è calcolabile mediante l’espressione
𝜎 = √𝑛𝑝𝑞
Non dimostreremo questa espressione ma la verificheremo nel caso particolare del
lancio di una moneta per 4 volte ossia calcoliamo la deviazione standard di questa
distribuzione tenendo presente che il valore medio è 𝜇 = 2 e i calcoli
precedentemente svolti. Risulta
1 4
1 4
1 4
2
2
2
2
𝜎 = (0 − 2) ∙ ( ) + (1 − 2) ∙ 4 ∙ ( ) + (1 − 2) ∙ 4 ∙ ( ) + (2 − 2)2 ∙ 6
2
2
2
4
4
1 4
1
1
16
∙ ( ) + (3 − 2)2 ∙ 4 ∙ ( ) + (4 − 2)2 ∙ ( ) =
=1
2
2
2
16
Se utilizziamo l’espressione equivalente si ottiene
1 1
𝜎 2 = 𝑛𝑝𝑞 = 4 ∙ ∙ = 1
2 2
Distribuzioni di probabilità continue
Una variabile aleatoria X, quando segue una distribuzione binomiale può assumere
solo valori interi. In circostanze diverse però i risultati di una variabile casuale
possono non essere limitati a valori interi, ossia la variabile aleatoria può essere
continua. A differenza delle variabili discrete, le variabili continue possono assumere
qualsiasi valore entro un certo intervallo e tra due qualsiasi valori esiste un numero
infinito di altri valori. La distribuzione di probabilità continua viene descritta con una
curva continua e la funzione che la descrive è chiamata densità di probabilità. A
differenza delle distribuzioni di probabilità discrete, l’altezza della curva in
corrispondenza di un certo valore della variabile casuale, non fornisce la probabilità
di ottenere proprio quel valore, ma indica la probabilità di ottenere quel valore entro
un certo intervallo della variabile casuale. Questa probabilità è data dall’area della
regione sottesa dalla curva tra gli estremi dell’intervallo. Per esempio la probabilità
che un singolo valore della variabile casuale, scelto casualmente sia compreso tra due
numeri a e b è uguale all’area della regione sottesa dalla curva tra a e b. Nel caso di
distribuzioni di probabilità continue, le aree sottese da queste distribuzioni sono
quindi rilevanti, non le altezze. ( Questo concetto è già stato visto durante la
trattazione degli istogrammi.) L’area della regione sottesa dalla curva tra a e b si
calcola integrando la funzione densità di probabilità tra i valori a e b. L’integrazione
81
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
è l’analogo per le variabili continue della somma, quindi integrare la funzione di
densità di probabilità tra i valori della variabile casuale compresi tra a e b analogo a
sommare la probabilità della variabile aleatoria per tutti i valori compresi tra a e b. (
Attenzione non ci pensiamo a calcolare gli integrali. Il simbolo di integrale viene
usato solo per correttezza formale, ma come si vedrà non useremo mai un integrale)
Per ogni distribuzione di probabilità, l’area della regione sottesa dall’intera curva di
una qualunque funzione di densità di probabilità continua è sempre uguale a 1 perché
dà la certezza che l’evento considerato si verifichi. Se 𝑓(𝑥) e una generica funzione
densità di probabilità, si ha quindi
+∞
∫
𝑓(𝑥)𝑑𝑥 = 1
−∞
Valore medio e varianza di una variabile statistica continua
Data una variabile continua con funzione di densità di probabilità 𝑓(𝑥), si definisce
valor medio 𝜇 di tale variabile è
+∞
𝜇=∫
𝑥𝑓(𝑥)𝑑𝑥
−∞
E’ la stessa definizione data per la variabile discreta ove al posto della somma si è
sostituito un integrale e al posto della probabilità si è sostituito la densità di
probabilità.
In analogia con quanto visto per la variabile casuale discreta, si definisce varianza di
una variabile continua con densità di probabilità 𝑓(𝑥) e valor medio 𝜇 il seguente
numero:
2
+∞
𝜎 =∫
(𝑥 − 𝜇)2 𝑓(𝑥)𝑑𝑥
−∞
La distribuzione normale
La distribuzione continua più comune è la distribuzione normale nota anche come
distribuzione di Gauss. E’ una distribuzione teorica di notevole interesse pratico per
le sue proprietà matematiche verranno utilizzate nei problemi d’inferenza statistica.
La distribuzione normale è specificata dalla seguente funzione di densità di
probabilità:
1 𝑥−𝜇 2
1
− (
)
𝑓(𝑥) =
𝑒 2 𝜎
𝜎√2𝜋
ove 𝜋 ed 𝑒 sono costanti i cui valori approssimati sono rispettivamente 3.14159 e
2.71828, 𝜎 e 𝜇 sono due parametri che rappresentano la deviazione standard e il
valore medio della distribuzione continua. L’equazione particolare di una determinata
curva normale può quindi essere ottenuta in base ai valori della media e della
82
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
deviazione standard; questo significa che è possibile ottenere diverse curve normali a
seconda dei valori di 𝜇 e 𝜎.
Ogni curva normale possiede le seguenti caratteristiche:
- è simmetrica rispetto al punto di ascissa 𝜇 in corrispondenza del quale si
trovano la media aritmetica, la moda e la mediana della distribuzione;
- è asintotica rispetto all’asse delle ascisse (cioè si avvicina all’asse delle ascisse
senza mai toccarlo) e quindi i valori delle ascisse variano da −∞ a +∞;
- è crescente da −∞ a 𝜇 e decrescente da 𝜇 a +∞;
- l’area racchiusa dall’intera curva è uguale a 1.
In base a queste proprietà possiamo dire che la distribuzione normale ha il suo valore
massimo in corrispondenza della media e la media, la mediana e la moda coincidono.
E’ possibile definire alcune regole pratiche relative alle aree delle regioni sottese
dalla curva normale.
Circa i 2/3 (più precisamente il 68.3%) dell’area sottesa dalla curva normale
corrispondono ad un intervallo individuato da una deviazione standard dalla media.
In altre parole la probabilità che un valore della variabile aleatoria sia compreso
nell’intervallo tra 𝜇 − 𝜎 e 𝜇 + 𝜎 è 0.683. In termini matematici se 𝑓(𝑥) e la
generica funzione densità di probabilità con media 𝜇 e deviazione standard 𝜎, si ha
quindi
𝜇+𝜎
∫
𝑓(𝑥)𝑑𝑥 = 0.683
𝜇−𝜎
Il 95% della probabilità di una distribuzione normale è compreso in un intervallo
individuato dal doppio della deviazione standard dalla media (più precisamente da
1.96 deviazioni standard. In altre parole, la probabilità che un valore della variabile
aleatoria sia compresa tra 𝜇 − 1.96𝜎 e 𝜇 + 1.96𝜎 è 0.95.
𝜇+1.96𝜎
∫
𝑓(𝑥)𝑑𝑥 = 0.95
𝜇−1.96𝜎
Molte variabili casuali (ad esempio statura, peso) sono distribuite normalmente e se
si conoscono la media e la deviazione standard delle loro distribuzioni siamo in
grado di stabilire la percentuale dei casi compresi in un determinato intervallo.
Questo fatto è particolarmente importante nell’ambito delle rilevazioni campionarie.
83
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Distribuzione normale standardizzata
E’ difficile calcolare la probabilità che una variabile aleatoria che segue una
distribuzione normale assuma un particolare valore perché richiede il calcolo di
un’area ossia l’integrazione di una funzione complicata.
D’altra parte è impossibile tabulare l’area associata ad ogni singola distribuzione
normale perché abbiamo un numero infinito di distribuzioni normali, una per ogni
coppia di 𝜇 e 𝜎.
Vediamo come risolvere il problema del calcolo delle aree. Supponiamo che X sia
una variabile casuale normale con media 2 e deviazione standard 0.5. Sottraendo 2 da
X otterremo una variabile casuale normale con media 0 e l’intera distribuzione
risulterebbe spostata a sinistra di due unità. Dividendo poi per 0.5 l’ampiezza della
distribuzione è alterata e si ha una variabile casuale normale con deviazione standard
1.
84
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Pertanto se X è una variabile casuale normale con media 2 e deviazione standard 0.5,
allora
𝑋−2
𝑍=
0.5
è una variabile casuale con medio 0 e deviazione standard 1.
Generalizzando: per standardizzare una qualunque variabile aleatoria X con media 𝜇
e deviazione standard 𝜎, occorre sottrarre a X la sua media e dividere poi per la sua
deviazione standard. In termini matematici
𝑋−𝜇
𝑍=
𝜎
e questa nuova variabile ha media 0 e scarto quadratico medio 1 cioè
𝜇𝑧 = 0
𝜎𝑧 = 1
qualunque sia la funzione di densità di probabilità. E’ chiamata variabile normale (o
casule) standardizzata.
Questa trasformazione permette di riportare una qualunque distribuzione normale con
media 𝜇 e deviazione standard 𝜎 ad una distribuzione avente media 0 e deviazione
standard 1. Tale distribuzione è chiamata distribuzione normale standardizzata e per
questa distribuzione sono state compilate delle tavole che ci permettono di
determinare la probabilità che interessano ciascun caso concreto.(quindi non
calcoleremo nessun integrale)
Come si leggono le tavole della normale standard
La prima colonna a sinistra della tavola riporta i valori z della variabile Z (avente
media 0 e deviazione standard 1) con la prima cifra decimale dei valori z; all’interno
della tavola all’incrocio della riga e della colonna che identificano un particolare
valore z con due cifre decimali, si legge la probabilità (area) che Z assuma valori
85
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
inferiori o uguali a quel valore z. Le caratteristiche di Z, in particolare la simmetria
della curva rispetto ad 0 e il fatto che l’area totale sotto la curva vale 1, fanno si che
questi valori sono sufficienti per calcolare la probabilità di qualunque intervallo.
Esempi di calcolo di probabilità di un qualunque intervallo di una
qualunque normale
Supponiamo per esempio che da dati ufficiali rilevati sulla popolazione normale,
risulti che il valore medio dell’HDL-colesterolo è 𝜇 = 57𝑚𝑔/100𝑚𝐿 con una
deviazione standard 𝜎 = 5 𝑚𝑔/100 𝑚𝐿. Sapendo che la distribuzione è di tipo
normale, vogliamo detrminare:
- la percentuale di valori HDL-colesterolo superiori a 60mg /100mL;
- la percentuale di valori HDL-colesterolo compresi tra 40 e 45 mg/100 mL;
- la percentuale di valori HDL-colesterolo compresi tra 55 e 58mg /100 mL.
Calcoliamo il valore della variabile Z quando la variabile X ha un valore pari a 60mg
/100mL. Si ha
𝑚𝑔
60 − 57
𝑥 = 60
𝑧=
= 0.60
100mL
5
Quindi calcolare la percentuale dei valori di che sono maggiori di 60 mg/100 mL
(ossia l’area sottesa dalla distribuzione normale avente 𝜇 = 57𝑚𝑔/100𝑚𝐿 e 𝜎 =
5 𝑚𝑔/100 𝑚𝐿 per valori della 𝑥 ≥ 60 𝑚𝑔⁄100𝑚𝐿) è equivalente a calcolare la
percentuale dei valori della distribuzione normale standardizzata per valori della
variabile z maggiori di 0.6 (ossia l’area sottesa dalla distribuzione di densità di
probabilità avente 𝜇 = 0 e 𝜎 = 1 per valori della variabile 𝑧 ≥ 0.6). Dalla tabella si
ottiene che quest’ultima area è 0.2743 ossia è il 27.43% del totale. Tale percentuale è
anche quella dei valori HDL-colesterolo superiori a 60mg/100 mL.
Analogamente per calcolare il valore della percentuale dei valori della curva normale
compresi tra 40 e 45 mg/mL, dobbiamo calcolare i valori corrispondenti della
variabile normale standardizzata e, successivamente, utilizzando i valori tabulati di
tale distribuzione, calcolare l’area compresa tra gli estremi calcolati.
Calcoliamo i valori della variabile normale standardizzata corrispondenti ai valori
della variabile normale dati dal problema. Si ha:
40 − 57
𝑥1 = 40 𝑚𝑔⁄100𝑚𝐿
𝑧1 =
= −3.4
5
45 − 57
𝑥2 = 45 𝑚𝑔⁄100𝑚𝐿
𝑧2 =
= −2.4
5
La tabella fornisce l’ area 𝐴1 da 2.4 all’infinito e l’area 𝐴2 da 3.4 all’infinito. Risulta
𝐴1 = 0.0082
𝐴2 = 0.0003
86
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
e, di conseguenza l’area cercata ossia la percentuale tra 2.4 e 3.4 è
𝐴 = 𝐴1 − 𝐴2 = 0.0082 − 0.0003 = 0.0079
Tale area dà la percentuale dei valori della variabile normale standardizzata compresi
tra 𝑧1 e 𝑧2 e quindi anche quella tra 𝑥1 e 𝑥2 .
Calcoliamo infine i valori della distribuzione normale compresi tra 𝑥1 =
55 𝑚𝑔⁄100𝑚𝐿 e 𝑥2 = 58 𝑚𝑔⁄100𝑚𝐿. I valori corrispondenti della variabile
normale standardizzata sono
55 − 57
𝑥1 = 55 𝑚𝑔⁄100𝑚𝐿
𝑧1 =
= −0.40
5
58 − 57
𝑥2 = 58 𝑚𝑔⁄100𝑚𝐿
𝑧1 =
= 0.20
5
L’area 𝐴1 compresa tra 𝑧1 e l’infinito è 0.0446 e quindi l’area 𝐴2 compresa tra 𝑧0 =
0 e 𝑧1 = −0.40 è 𝐴2 = 0.5 − 0.3446 = 0.1554
L’area 𝐴3 compresa tra 𝑧2 e l’infinito è 0.4207 e quindi l’area 𝐴4 compresa tra 𝑧0 =
0 e 𝑧2 = 0.20 è 𝐴4 = 0.5 − 0.4207 = 0.0793.
Di conseguenza l’area compresa tra 𝑧1 e 𝑧2 è
𝐴 = 𝐴3 + 𝐴4 = 0.1554 + 0.0793 = 0.2347
Tale area è equivalente a quella compresa tra 𝑥 e 𝑥2 e quindi fornisce la percentuale
dei valori cercati relativi alla variabile normale.
Alcuni intervalli tipici
Molto interessante per l’ inferenza statistica e per la teoria della stima è il problema
opposto. Vogliamo calcolare per quali valori della variabile normale standardizzata
l’area su entrambe le code di tale distribuzione è il 5% o 1% del totale.
Poiché la percentuale dei valori su entrambe le code deve essere 0.05 ed essendo la
distribuzione normale simmetrica, l’area staccata su ogni coda deve essere 0.025.
Tale area si ottiene integrando la funzione di distribuzione normale standardizzata tra
1.96 e l’infinito
2
+∞ −𝑧
2
∫1.96 𝑒
𝑑𝑧
= 0.025
√2𝜋
Possiamo quindi affermare che i valori della variabile normale standardizzata che
staccano il 5% dell’area totale sono
𝑧1 = −1.96
𝑧2 = 1.96
Naturalmente l’area della normale standardizzata per −1.96 ≤ 𝑧 ≤ 1.96 è 0.95 ossia
è il 95% dell’area totale.
Questo procedimento è generale e quindi applicandolo nel caso dell’1% si ha che i
valori di z sono ±2.58 ossia i valori della variabile normale standardizzata che
staccano l’ 1% dell’area totale sono
𝑧1 = −2.58
𝑧2 = 2.58
87
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Naturalmente l’area della normale standardizzata per −2.58 ≤ 𝑧 ≤ 2.58 è 0.99 ossia
è il 99% dell’area totale.
Il valore di z che stacca, ad esempio, l’1% su una coda soltanto è diverso da valori
precedenti. Infatti, applicando lo stesso procedimento si ottiene 𝑧 = 2.32
Questo per la variabile normale standardizzata. I valori della variabile X avente
media 𝜇 e deviazione standard 𝜎 che staccano il 5% dell’area totale sono, di
conseguenza,
𝑋−𝜇
−1.96 ≤
≤ 1.96
𝜎
e quindi
𝜇 − 1.96𝜎 ≤ 𝑋 ≤ 𝜇 + 1.96𝜎
Analogamente nel caso dell’1%, si ha
𝜇 − 2.58𝜎 ≤ 𝑋 ≤ 𝜇 + 2.58
Esercizi
Esercizio 1
Si spieghi la differenza fra eventi mutuamente esclusivi ed eventi indipendenti
Due eventi A e B che non possono verificarsi contemporaneamente sono definiti
mutuamente esclusivi.
Due eventi A e B sono indipendenti quando il verificarsi di A non ha alcuna
influenza sul verificarsi o non verificarsi di B
Esercizio 2
Quali sono i parametri che definiscono una distribuzione binomiale.
I parametri che definiscono una distribuzione binomiale sono il numero delle prove 𝑛
e la probabilità di successo 𝑝 (costante) in ogni prova.
Esercizio 3
Quali sono le tre assunzioni associate alla distribuzione binomiale?
Si ha un numero fisso 𝑛 di prove ognuna delle quali dà luogo a due risultati
mutuamente esclusivi, il successo e l’insuccesso
In ogni prova la probabilità di successo (insuccesso) è costante.
I risultati delle 𝑛 prove sono mutuamente esclusivi.
88
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Esercizio 4
Molte coppie preferirebbero avere un figlio di ciascun sesso. La probabilità di avere
un maschio è 0.512, mentre la probabilità di avere una femmina è 0.488.Se la coppia
decide di avere soltanto due figli, qual è la probabilità di avere un figlio di ciascun
sesso? Qual è la probabilità che nasca almeno una femmina?
Calcoliamo la probabilità di avere un figlio di ciascun sesso in una famiglia con due
figli. Indichiamo con M l’evento “nascita di un maschio” e con F l’evento “nascita di
una femmina”. I due eventi sono incompatibili e le sequenze alternative che
determinano la nascita di un maschio e di una femmina sono
𝑀𝐹
𝐹𝑀
Vogliamo determinare la probabilità che si verifichi la prima oppure la seconda
sequenza perché entrambe producono un maschio e una femmina. La probabilità 𝑃1
della prima sequenza è il prodotto delle probabilità di ogni evento, perché gli eventi
sono indipendenti. Quindi
𝑃1 = 0.512 × 0.488 = 0.250
In modo analogo si procede per il calcolo della probabilità della seconda sequenza e
si ottiene
𝑃2 = 0.488 × 0.512 = 0.250
La probabilità che si verifichi la prima oppure la seconda sequenza è la somma delle
probabilità delle due sequenze alternative e si ha
𝑃 = 𝑃1 + 𝑃2 = 0.250 + 0.250 = 0.500
Calcoliamo ora la probabilità che nasca almeno una femmina in una famiglia con due
figli. Le sequenze alternative sono:
𝑀𝐹 𝐹𝑀 𝐹𝐹
e le rispettive probabilità sono:
𝑃1 = 0.512 × 0.488 = 0.250
𝑃2 = 0.488 × 0.512 = 0.250 𝑃3
= 0.488 × 0.488 = 0.238
La probabilità che in una famiglia con due figli ci sia almeno una femmina è
𝑃(𝑎𝑙𝑚𝑒𝑛𝑜 𝑢𝑛𝑎 𝑓𝑒𝑚𝑚𝑖𝑛𝑎) = 0.250 + 0.250 + 0.238 = 0.738
Alternativamente si poteva utilizzare la distribuzione binomiale per calcolare la
probabilità che ad esempio in una famiglia con due figli ci sia almeno una figlia.
Dobbiamo trovare il numero delle prove 𝑛 e la probabilità costante in ogni prova.
Abbiamo un evento che può verificarsi secondo due modalità e indichiamo l’evento
“nascita di una femmina” come evento successo e quindi la sua probabilità è 0.488.
La famiglia ha due figli e quindi il numero delle prove è 2. La probabilità di avere
almeno un successo su due prove è la somma delle probabilità di avere un successo
con la probabilità di avere due successi ossia
2!
2!
𝑃(𝑎𝑙𝑚𝑒𝑛𝑜 𝑢𝑛𝑎 𝑓𝑒𝑚𝑚𝑖𝑛𝑎) =
0.488 × 0.512 +
0.4882 × 0.5120
1! × 1!
2! × 0!
= 0.738
89
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Esercizio 5
Quali delle seguenti caratteristiche possiamo associare alla distribuzione normale?
1) simmetria; 2) la media è uguale alla mediana; 3) La media è uguale alla moda
4) asimmetria positiva.
a) solo 1, 2 e 3
b) solo 1 e 2
c) solo 2 e 4
d) solo 4
e) tutte le 4 caratteristiche.
La distribuzione normale è simmetrica e la media, la mediana e la moda coincidono.
Di conseguenza la risposta corretta è la a)
Esercizio 6
Una distribuzione normale ha media 15 e deviazione standard 3. Quale intervallo
include circa il 95% di probabilità?
a) 12-18
b) 9-21
c) 6-34
d) 3-27
e) nessuna delle precedenti risposte.
L’intervallo che comprende circa il 95% dei valori è quelle compreso tra il valore
medio e ±2𝜎. Nel nostro caso l’intervallo ha come estremi 15 − 2 ∙ 3 = 9 e 15 + 2 ∙
3 = 21. Quindi la risposta corretta è la b). Per ottenere l’intervallo esatto bisogna
sostituire 1.96 al posto di 2 e quindi si avrebbe 15 − 1.96 ∙ 3 = 9.12 e 15 + 1.96 ∙
3 = 20.88.
90
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
91
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Teoria elementare del campionamento
La teoria dei campioni è lo studio delle relazioni esistenti tra una popolazione ed i
campioni estratti dalla popolazione stessa Tale teoria è di grande importanza perché
permette di inferire le proprietà di una popolazione quali la media, la varianza, la
deviazione standard e così via (che chiameremo genericamente parametri) sulla base
di osservazioni relative ad un campione (teoria della stima) oppure permette di
estendere, in termini probabilistici, a tutta la popolazione le conclusioni relative al
campione stesso (verifica di ipotesi).
Distribuzione campionaria delle medie
Effettuare un campionamento di un parametro di una popolazione, per esempio
effettuare il campionamento della media, significa estrarre da una data popolazione
avente media 𝜇 e deviazione standard 𝜎, un campione casuale di 𝑛 osservazioni e
calcolare la media di questo campione. Indichiamo tale media con ̅̅̅.
𝑥1 Selezioniamo
poi un secondo campione casuale di 𝑛 osservazioni e calcoliamo la media del nuovo
campione. Indichiamo tale media con ̅̅̅.
𝑥2 Se eseguiamo questa procedura all’infinitoselezionando tutti i possibili campioni di dimensione 𝑛 e calcolando le loro medieotterremo una serie di valori costituiti da medie campionarie. Ciascuna media della
serie è considerata una singola osservazione e la distribuzione di queste medie è
denominata la distribuzione campionaria delle medie di campioni di dimensione 𝑛.
Dunque la variabile statistica campionata è la media.
La distribuzione campionaria delle media calcolata per campioni di dimensione 𝑛, ha
tre importanti proprietà:
1) la media della distribuzione campionaria è uguale alla media 𝜇 della
popolazione.
𝜇𝑥̅ = 𝜇
2) La deviazione standard della distribuzione delle medie campionarie è chiamata
errore standard della media è uguale a
𝜎
𝜎𝑥̅ =
√𝑛
3) La forma della distribuzione campionaria è approssimativamente normale,
posto che 𝑛 sia sufficientemente grande, ossia la variabile statistica “media” ha
una distribuzione campionaria normale se l’ampiezza del campione è
sufficientemente grande.
92
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Dimostrare le prime due proprietà per una popolazione infinitamente grande è molto
complesso. Le dimostreremo nel caso di una popolazione finita. Supponiamo dunque
di avere una variabile statistica che può assumere soltanto i seguenti cinque valori:
15 20 25 30 35
Su questa popolazione calcoliamo la media e la varianza. Si ha:
∑51 𝑥𝑖 15 + 20 + 25 + 30 + 35
𝜇=
=
= 25
5
5
∑51(𝑥𝑖 − 𝜇)2 102 + 52 + 52 + 102
𝜎 =
=
= 50
5
5
2
Da questa popolazione finita, fissata la dimensione del campione , potremo ottenere
un certo numero di campioni. Su ciascun campione possono essere calcolati diversi
parametri; ci limiteremo ai parametri più significativi: la media e la varianza.
L’insieme delle medie di tutti i possibili campioni costituisce la distribuzione
campionaria delle medie, così come l’insieme delle varianze rappresenta la
distribuzione campionaria delle varianze.
Supponiamo di mettere ogni singolo valore della variabile casuale all’interno di una
pallina e mettere le cinque palline in un’urna. Estraiamo una pallina alla volta ,
osserviamo il numero, la rimettiamo nell’urna e procediamo all’estrazione di
un’altra pallina. (estrazione bernoulliana)
Immaginiamo di estrarre da questa popolazione campioni di ampiezza 𝑛 = 2. Nella
tabella successiva viene rappresentata la distribuzione campionaria della media e
della varianza.
N
1
2
3
4
5
6
7
8
9
10
11
Campioni estratti media varianza
15−15
15−20
15− 25
15−30
15 −35
20 −15
20− 20
20 −25
20 −30
20−35
25 −15
15
17.5
20
22.5
25
17.5
20
22.5
25
27.5
20
0.00
6.25
25.00
56.25
100.00
6.25
0.00
6.25
25.00
56.25
6.25
93
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
12
13
14
15
16
17
18
19
20
21
22
23
24
25
25− 20
25− 25
25− 30
25− 35
30 −15
30−20
30−25
30−30
30−35
35−15
35−20
35−25
35−30
35−35
22.5
25
27.5
30
22.5
25
27.5
30
32.5
25
27.5
30
32.5
35
6.25
0.00
6.25
25.00
56.25
25.00
6.25
0.00
6.25
100.00
56.25
25.00
6.25
0.00
La distribuzione delle frequenze è la seguente
Media Frequenze assolute Frequenze relative
15
1
0.04
17.5
2
0.08
20
3
0.12
22.5
4
0.16
25
5
0.20
27.5
4
0.16
30
3
0.12
32.5
2
0.08
35
1
0.04
Su questa distribuzione calcoliamo la media e la varianza campionaria
Si ha
𝜇𝑥̅
15 + 17.5 × 2 + 20 × 3 + 22.5 × 4 + 25 × 5 + 27.5 × 4 + 30 × 3 + 32.5 × 2 + 35
=
25
= 25
𝜎𝑥̅2
102 + 7.52 × 2 + 52 × 3 + 2.52 × 4 + 02 × 5 + 2.52 × 4 + 52 × 3 + 7.52 × 2 + 102
=
25
= 25
94
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Se ora confrontiamo i valori della popolazione con quelli della distribuzione
campionaria otteniamo le seguenti relazioni:
𝜇𝑥̅ = 𝜇
ossia la media della popolazione è uguale alla media della distribuzione campionaria;
e
𝜎2
2
𝜎𝑥̅ =
𝑛
cioè la varianza della distribuzione campionaria è uguale alla varianza della
popolazione diviso l’ampiezza del campione.
L’enunciato della terza proprietà è noto come teorema del limite centrale. Questo
risultato si applica ad ogni popolazione con una deviazione standard finita,
indipendentemente dalla forma della distribuzione originaria.
Se la distribuzione originaria è normale, anche la distribuzione della media
campionaria avrà una distribuzione normale. Più la popolazione originaria si
allontana da una distribuzione normale , però, maggiore sarà il valore di 𝑛 necessario
ad assicurarsi la normalità della distribuzione campionaria. Nel caso in cui la
popolazione è bimodale o notevolmente asimmetrica, è spesso sufficiente un
campione di dimensione uguale a 30. Il teorema del limite centrale è molto potente e
si applica non solo alle variabili casuali continue ma anche alle discrete.
In conclusione per ampiezze del campione sufficientemente elevate, la distribuzione
campionaria delle medie è bene approssimata da una distribuzione normale con
media e varianza date dalle espressioni viste precedentemente. Di conseguenza la
quantità
𝑥̅ − 𝜇
𝑧= 𝜎
√𝑛
definisce una variabile casuale normale standardizzata ossia con media 1 e
deviazione standard 0.
Distribuzione campionaria delle proporzioni
Supponiamo ora di avere una popolazione relativa a un carattere nominale binomiale
(successo/insuccesso). Per esempio la popolazione può essere costituita da pazienti ai
quali è stato diagnosticato un cancro al polmone, e indichiamo la sopravvivenza a 5
anni con 1 e la morte con 0. Poiché la popolazione è di tipo binomiale, tenendo
presente le proprietà di tale distribuzione teorica, si ha che i parametri che la
definiscono sono
𝜇=𝑝
𝜎 2 = 𝑝𝑞
Supponiamo di selezionare dalla popolazione un campione casuale di dimensione 𝑛 e
indichiamo la proporzione di successi nel campione con ̂.
𝑝1 Allo stesso modo,
95
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
possiamo selezionare un secondo campione di dimensione 𝑛 e indicare la proporzione
di successi con 𝑝
̂.
2 Se trattassimo ogni proporzione come una unica osservazione, la
loro distribuzione collettiva è una distribuzione campionaria delle proporzioni per
campioni di dimensione 𝑛. La distribuzione campionaria delle proporzioni ha le
seguenti tre proprietà:
1) la media 𝜇 della distribuzione campionaria è la media 𝑝 della popolazione
𝜇=𝑝
2) la deviazione standard della distribuzione campionaria delle proporzioni 𝜎𝑝̂ è
detta errore standard di una proporzione ed è uguale a
𝑝𝑞
𝜎𝑝̂ = √
𝑛
3) La forma della distribuzione campionaria è approssimativamente normale
posto che 𝑛 sia sufficientemente grande.
Poiché la distribuzione campionaria delle proporzioni è approssimativamente
normale con media 𝑝 e deviazione standard √𝑝𝑞⁄𝑛, sappiamo che
𝑍=
𝑝̂ − 𝑝
𝑝𝑞
𝑛
è normalmente distribuita con media 0 e deviazione standard 1. Pertanto possiamo
utilizzare la tabella della distribuzione normale standardizzata per fare delle inferenze
sul valore della proporzione di una popolazione.
√
Intervalli di confidenza
Abbiamo esaminato le proprietà teoriche della distribuzione campionaria delle medie
e della distribuzione campionaria delle proporzioni. Applichiamo ora questi risultati
al processo dell’inferenza statistica. Il nostro primo obiettivo è la stima di alcune
caratteristiche di una variabile casuale continua – come la sua media o la varianzautilizzando le osservazioni contenute in un campione.
Stima puntuale e stima intervallare
Di solito si utilizzano due metodi di stima. Il primo è denominato stima puntuale ed
implica il calcolo di un singolo numero per stimare il parametro in esame.
Supponiamo di avere estratto un campione bernoulliano di ampiezza 𝑛, per fare una
96
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
stima puntuale della media 𝜇 della popolazione si utilizza la media 𝑥̅ del campione,
mentre per fare una stima puntuale della varianza si utilizza la varianza campionaria
corretta.
1
Media campionaria (stima) 𝑥̅ = ∑𝑛𝑖 𝑥𝑖
𝑛
Varianza campionaria corretta
𝑠2 =
1
𝑛−1
∑𝑛1(𝑥𝑖 − 𝑥̅ )2
Inoltre in ambito biomedico sono interessanti i fenomeni categoriali in special modo
quelli dicotomici cioè quelli che si manifestano con due sole modalità contrarie ed
esaustive: si/no, favorevole/contrario, sopravvissuto/non sopravvissuto. L’oggetto
della stima in questi casi è la percentuale di casi che è classificabile in una data
categoria. Oggetto dell’inferenza in questi casi è la percentuale di una data categoria..
Si sceglie l’ampiezza del campione, si estrae il campione e il risultato sarà un
insieme di unità statistiche classificabili o non classificabili nella categoria che ci
interessa. La stima per l’ignota frequenza relativa p di soggetti classificabili nella
categoria di interesse è la corrispondente frequenza relativa nel campione cioè è la
frequenza relativa campionaria che indicheremo con 𝑝̂ (pi cappello).
Stima della percentuale p
1
𝑝̂ = ∑𝑛𝑖 𝑥𝑖
𝑛
ove la somma dei dati campionari ∑𝑛𝑖 𝑥𝑖 ci da il numero di soggetti campionati che,
fra gli n estratti, sono classificabili nella categoria che ci interessa. Dividendo tale
somma per l’ampiezza del campione si ottiene la stima cercata. In formule la stima 𝑝̂
ha allora la stessa forma della media campionaria.
Tuttavia una stima puntuale non fornisce alcuna informazione sulla vicinanza della
stima al valore vero della popolazione. Pertanto, spesso, si preferisce un secondo
metodo, denominato stima intervallare. Questa tecnica fornisce un range di possibili
valori entro i quali si ritiene sia compreso il valore del parametro in esame ( in questo
caso la media della popolazione) con una certa probabilità, con un certo grado di
confidenza. Questo range di valori è denominato intervallo di confidenza.
Intervallo di confidenza per la media 𝜇 con popolazione normale e
varianza nota
Per calcolare un intervallo di confidenza per 𝜇 ci basiamo sulla distribuzione
campionaria della media. Data una variabile casuale X con media 𝜇 e deviazione
standard 𝜎, il teorema del limite centrale afferma che
97
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
𝑋̅ − 𝜇
𝜎
√𝑛
ha una distribuzione normale standardizzata se X è normalmente distribuita e una
distribuzione normale standardizzata approssimativa se non lo è, ma 𝑛 è
sufficientemente grande. Per una variabile casuale normale standardizzata, il 95%
delle osservazioni è compreso tra −1.96 e 1.96. In altre parole, la probabilità che Z
assuma un valore compreso tra −1.96 e 1.96 è il 95% cioè
𝑍=
𝑃(−1.96 ≤ 𝑍 ≤ 1.96) = 0.95
Allo stesso modo, possiamo sostituire a Z la sua espressione e scrivere:
𝑥̅ − 𝜇
𝜎 ≤ 1.96) = 0.95
√𝑛
Moltiplicando i tre termini della disuguaglianza per l’errore standard 𝜎⁄√𝑛 e
sottraendo poi 𝑥̅ da ciascun termine, si ha
𝜎
𝜎
𝑃 (−1.96
− 𝑥̅ ≤ −𝜇 ≤ 1.96
− 𝑥̅ ) = 0.95
√𝑛
√𝑛
Infine moltiplichiamo per −1, tenendo presente che quando si moltiplica una
disuguaglianza per un numero negativo si inverte la direzione della disuguaglianza, e
si ottiene
𝜎
𝜎
𝑃 (𝑥̅ − 1.96
≤ 𝜇 ≤ 𝑥̅ + 1.96 ) = 0.95
√𝑛
√𝑛
𝑃 (−1.96 ≤
Le quantità 𝑥̅ − 1.96
𝜎
√𝑛
e 𝑥̅ + 1.96
𝜎
√𝑛
sono i limiti dell’intervallo di confidenza al
95% per la media 𝜇 della popolazione. I valori −1.96 𝑒 1.96 sono chiamati “valori
critici al 5%” , il 95% e chiamato “livello di fiducia” e il 5% “livello di
significatività”.
In conclusione l’intervallo
(𝑥̅ − 1.96
𝜎
, 𝑥̅ + 1.96
𝜎
)
√𝑛
√𝑛
ha una probabilità del 95% di comprendere la media reale 𝜇 della popolazione.
Si faccia attenzione che la probabilità riguarda l’intervallo non la media vera, cioè
non diciamo che esiste una probabilità del 95% che la media vera sia compresa tra i
sopraddetti limiti - questa affermazione è sbagliata perché la media della popolazione
è un valore fisso, non è una variabile aleatoria, e non può essere associato ad una
probabilità- ma diciamo che siamo fiduciosi al 95% che la media vera sia compresa
tra i limiti precedentemente specificati.
98
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Sebbene l’intervallo di confidenza più applicato sia quello al 95% esso non è l’unico
utilizzabile. Potremmo preferire un maggior grado di confidenza relativamente al
valore della media della popolazione; in questo caso potremmo scegliere di calcolare
un intervallo di confidenza al 99%. Poiché il 99% delle osservazioni in una
distribuzione normale standardizzata è compreso tra −2.58 e 2.58 , un intervallo di
confidenza al 99% per 𝜇 è
(𝑥̅ − 2.58
𝜎
, 𝑥̅ + 2.58
𝜎
)
√𝑛
√𝑛
e −2.58 𝑒 2.58 sono detti “valori critici al 1%” e il 99% è detto “livello di fiducia”
Come atteso, l’intervallo di confidenza al 99% è più ampio dell’intervallo al 95%.
Se vogliamo restringere un intervallo senza ridurre il livello di confidenza, abbiamo
bisogno di maggiori informazioni sulla media della popolazione; dobbiamo quindi
selezionare un campione più ampio. All’aumentare della dimensione 𝑛 del campione,
l’errore standard 𝜎⁄√𝑛 diminuisce; ciò determina un intervallo di confidenza più
ristretto. Si considerino, ad esempio, i limiti dell’intervallo di confidenza al 95%. Se
selezioniamo un campione di dimensione uguale a 10 i limiti di confidenza sono 𝑥̅ ±
1.96(𝜎⁄√10) e quindi l’ampiezza dell’intervallo è
0.620𝜎 + 0.620𝜎 = 1.240𝜎. Se il campione selezionato è di dimensione uguale a
100 i limiti di confidenza sono 𝑥̅ ± 1.96(𝜎⁄√100) e quindi l’ampiezza
dell’intervallo è 0.196𝜎 + 0.196𝜎 = 0.392𝜎.
Quanto detto è valido per popolazioni distribuite normalmente con 𝜎 noto o
comunque per campioni abbastanza numerosi (𝑛 > 50) per i quali la distribuzione
campionaria della media è normale.
99
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Esempio1
Si consideri la distribuzione dei livelli di colesterolo sierico della popolazione
maschile negli Stati Uniti di ipertesi e fumatori. Questa distribuzione è
approssimativamente normale con media 𝜇 non nota e una deviazione standard 𝜎 =
46 𝑚𝑔⁄100𝑚𝑙. (Assumiamo che 𝜎 sia uguale a quella della popolazione generale di
maschi adulti negli Stati Uniti, anche se la media può essere diversa). Vogliamo
stimare il livello medio di colesterolo sierico di questa popolazione.
Per fare ciò dobbiamo estrarre un campione e valutare da esso 𝑥̅ . Supponiamo di
selezionare un campione di dimensione uguale a 12 dalla popolazione di ipertesi
fumatori e che questi soggetti abbiano un livello medio di colesterolo sierico 𝑥̅ =
217 𝑚𝑔⁄100𝑚𝐿. In base a questo campione, l’intervallo di confidenza al 95% per la
media 𝜇 della popolazione è:
46
46
; 217 + 1.96
(217 − 1.96
)
√12
√12
ossia
(191; 243)
La nostra miglior stima per il livello medio di colesterolo sierico della popolazione
maschile di ipertesi fumatori è 217 𝑚𝑔⁄100𝑚𝐿; tuttavia l’intervallo da 191 a 243 ci
fornisce un range di valori accettabili per 𝜇. (Si noti che questo valore comprende il
valore 211 𝑚𝑔⁄100 𝑚𝐿 che è il livello medio di colesterolo sierico per tutti i maschi
di età compresa tra 20 e 74 anni negli Stati Uniti, indipendentemente
dall’ipertensione o dall’atteggiamento dei confronti del fumo) Siamo confidenti al
95% che i limiti 191 e 243 comprendano la media reale 𝜇.
Invece di calcolare un intervallo di confidenza al 95% per il livello di colesterolo
sierico, potremmo calcolare un intervallo di confidenza al 99% per il parametro 𝜇.
Utilizzando lo stesso campione di 12 ipertesi fumatori, troviamo che i limito sono
46
46
; 217 + 2.58
(217 − 2.58
)
√12
√12
ossia
(183; 251)
come già osservato, questo intervallo è più ampio dell’intervallo di confidenza al
95%. L’intervallo di confidenza al 99% ha ampiezza 251 − 183 = 68 𝑚𝑔⁄100 𝑚𝐿
mentre l’intervallo di confidenza al 95% ha ampiezza 243 − 191 =
52 𝑚𝑔⁄100 𝑚𝐿.
Ci chiediamo ora quanto dovrebbe essere grande un campione per ridurre l’ampiezza
dell’intervallo a 20 𝑚𝑔⁄100 𝑚𝐿 a livello del 99%? L’ampiezza dell’intervallo è
data dalla semidifferenza tra il valore superiore e quello inferiore ossia da
46
2.58
= 10
√𝑛
Risolvendo si ha
2.58
46
√𝑛 =
10
100
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
𝑛 = 140.8
√𝑛 = 11.87
Per ridurre l’ampiezza dell’intervallo di confidenza al 99% a 20 𝑚𝑔⁄100 𝑚𝐿
dobbiamo selezionare un campione di 141 soggetti. Si osservi che l’ampiezza
dell’intervallo non dipende dalla media ma solo da 𝜎, 𝑛 e dal livello di confidenza.
Intervallo di confidenza per la media 𝜇 con popolazione normale e
varianza incognita
Distribuzione t di Student.
Nel calcolare gli intervalli di confidenza per una media 𝜇 non nota, abbiamo sempre
assunto che 𝜎, la deviazione standard della popolazione, sia nota. In realtà ciò è
improbabile; generalmente anche 𝜎 non è nota. In questo caso invece di utilizzare la
distribuzione normale standardizzata, si utilizza una nuova distribuzione di
probabilità nota come distribuzione t di Student. (pseudonimo usato dallo statistico
che ha scoperto questa distribuzione) e gli intervalli di confidenza sono calcolati in
modo simile.
Per calcolare un intervallo di confidenza per la media 𝜇 della popolazione, notiamo
prima di tutto che:
𝑋̅ − 𝜇
𝑍= 𝜎
√𝑛
ha una approssimata distribuzione normale standardizzata se 𝑛 è sufficientemente
grande. Quando la deviazione standard della popolazione non è nota e si hanno
piccoli campioni, anziché utilizzare l’errore standard
𝜎
𝜎𝑥̅ =
√𝑛
utilizziamo una sua stima
𝑠
√𝑛
Il numeratore di questa espressione è la deviazione standard campionaria corretta (𝑠)
che è una stima puntuale della deviazione standard vera (𝜎) ossia è:
𝑛
1
𝑠2 =
∑(𝑥𝑖 − 𝑥̅ )2
𝑛−1
1
Ma il rapporto
𝑋̅ − 𝜇
𝑍= 𝑠
√𝑛
101
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
non ha una distribuzione normale standardizzata perché 𝑠 varia da campione a
campione per effetto del caso e quindi 𝑠⁄√𝑛 non è costante come 𝜎𝑥̅ .
Se X è normalmente distribuita ed un campione casuale di dimensione 𝑛 è selezionata
da questa popolazione originaria, la distribuzione di probabilità della variabile
casuale
𝑋̅ − 𝜇
𝑡= 𝑠
√𝑛
è nota come distribuzione t di Student con 𝑛 − 1 gradi di libertà.
Il numero dei gradi di libertà (gl) è un ulteriore parametro di questa distribuzione. E’
data dalla dimensione campionaria meno 1:
𝑔𝑙 = 𝑛 − 1
Utilizzeremo in questo caso la notazione 𝑡𝑛−1 . Dunque prima di calcolare il valore
critico di t dobbiamo calcolare i gradi di libertà. Come la distribuzione normale
standardizzata, la distribuzione t è unimodale e simmetrica intorno alla sua media che
è 0 e l’area totale sotto la curva è uguale a 1.
Per ogni possibile valore dei gradi di libertà, c’è una diversa distribuzione di t. Le
distribuzioni con pochi gradi di libertà hanno una maggiore dispersione,
all’aumentare dei gradi di libertà, la distribuzione t si avvicina alla normale
standardizzata. Ciò si verifica perché, all’aumentare della dimensione del campione,
𝑠 diventa una stima più affidabile di 𝜎; se 𝑛 è molto grande , conoscere il valore di 𝑠
equivale a conoscere il valore di 𝜎(come visto nell’esempio precedente).
Poiché c’è una diversa distribuzione t per ogni grado di libertà, sarebbe alquanto
complesso avere una tabella completa delle aree corrispondenti a ciascun possibile
102
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
valore. Pertanto per un determinato valore dei gl, si sono tabulati solo i valori critici.
La tabulazione è avvenuta nel modo seguente.
Per esempio si consideri una distribuzione t corrispondente ad un certo grado di
libertà ad esempio 10; in corrispondenza al livello di significatività del 5% il valore
𝑡10 = 2.228 delimita il 2.5% superiore dell’area sotto la curva. Poiché la
distribuzione è simmetrica, 𝑡10 = −2.228 delimita il 2.5% inferiore. Si osservi che
per la curva normale standardizzata, 𝑧 = 1.96 delimita il 2.5% superiore della
distribuzione e quindi all’aumentare di n, la t di Student si avvicina a questo valore.
In realtà quando abbiamo più di 30 gradi di libertà, possiamo sostituire la
distribuzione normale standardizzata alla t ( in questo caso l’imprecisione sarà
minore del 5%).
Esempio. Siano
100 120 100 90 110 120 80 160
le pressioni arteriose, espresse in mm Hg, di 8 soggetti; si calcoli l’intervallo di
confidenza della media al 99%. Si ha
∑(𝑥𝑖 − 𝑥̅ )2
2
𝑥̅ = 110
𝑠 =
= 600
𝑠 = 24.5
𝑛−1
Il valore di t con 7 g.l. per 0.005 su entrambe le code è 𝑡0.01,7 = 3.499. Di
conseguenza gli estremi dell’intervallo di confidenza della media a livello di fiducia
del 99% sono
24.5
24.5
110 − 3.499
110 + 3.499
√8
√8
quindi l’intervallo avente valori estremi80 e 140 mm di Hg ha una probabilità del
99% di contenere il vero valore della pressione media di tutti i soggetti omogenei
(cioè con uguali caratteristiche) a quelli osservati.
Intervallo di confidenza per una proporzione.
Per calcolare un intervallo di confidenza per la proporzione di una popolazione,
seguiamo la stessa procedura adottata per la media di una popolazione. Prima di tutto
selezioniamo un campione di dimensione 𝑛 e usiamo queste osservazioni per
calcolare la proporzione del campione 𝑝̂ ; questo valore è una stima puntuale di 𝑝.
Come già detto
𝑝̂ − 𝑝
𝑍=
√𝑝(1 − 𝑝)
𝑛
103
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
è una variabile normale standardizzata con media 0 e varianza 1, se 𝑛 è
sufficientemente grande. Sappiamo che per una distribuzione normale standardizzata
il 95% dei possibili risultati giace tra −1.96 e 1.96. Quindi
𝑃 (−1.96 ≤
𝑝̂ − 𝑝
√𝑝(1 − 𝑝)⁄𝑛
≤ 1.96) = 0.95
e, di conseguenza
𝑝(1 − 𝑝)
𝑝(1 − 𝑝)
𝑃 (𝑝̂ − 1.96√
≤ 𝑝 ≤ 𝑝̂ + 1.96√
) = 0.95
𝑛
𝑛
I termini 𝑝̂ − 1.96√𝑝(1 − 𝑝)⁄𝑛 e 𝑝̂ + 1.96√𝑝(1 − 𝑝)⁄𝑛 sono i limiti dell’intervallo
di confidenza al 95% per la proporzione 𝑝 della popolazione. Tuttavia queste quantità
dipendono dal valore di 𝑝. Poiché 𝑝 non è nota, dobbiamo stimarla utilizzando la
proporzione campionaria 𝑝̂ . Pertanto l’intervallo di confidenza approssimato al 95%
per 𝑝 è
𝑝̂ (1 − 𝑝̂ )
𝑝̂ (1 − 𝑝̂ )
; 𝑝̂ + 1.96√
(𝑝̂ − 1.96√
)
𝑛
𝑛
Esempio. Si consideri la distribuzione della sopravvivenza a cinque anni dei pazienti
al di sotto di 40 anni ai quali è stato diagnosticato un cancro del polmone. Questa
distribuzione ha una media della popolazione 𝑝 non nota. In un campione casuale di
52 pazienti, solo 6 sopravvivono 5 anni. Quindi
𝑥
6
𝑝̂ = =
= 0.115
𝑛 52
è una stima puntuale di 𝑝. Si può dimostrare (infatti risulta 𝑛𝑝̂ = 6 e 𝑛(1 − 𝑝̂ ) = 52 ∙
(1 − 0.115) = 46.0)che la dimensione del campione è sufficientemente grande per
giustificare l’uso dell’approssimazione alla normale e quindi un intervallo di
confidenza approssimato al 95% per 𝑝 è
0.115(1 − 0.115)
0.115(1 − 0.115)
(0.115 − 1.96√
; 0.115 + 1.96√
52
52
oppure
(0.028; 0.202)
In conclusione: 0.115 è la nostra miglior stima per la proporzione della popolazione e
siamo confidenti al 95% che l’intervallo precedente comprenda la proporzione reale
di pazienti al di sotto di 40 anni che sopravvivono a 5 anni.
104
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
La variabile associata alla proporzione è distribuita come una binomiale, e quando 𝑛
è piccolo non può essere approssimata a una normale. In questo caso il calcolo degli
estremi dell’intervallo è molto laborioso e non lo considereremo
Esercizi
Esercizio 1
Come si interpreta l’intervallo di confidenza al 95% per la media 𝜇 di una
popolazione?
L’intervallo di confidenza al 95% è l’intervallo che ha una probabilità del 95% di
comprendere la media reale 𝜇 della popolazione.
Esercizio 2
L’errore standard della media di un campione
a) misura la variabilità delle osservazioni;
b) è l’accuratezza con cui ogni osservazione viene misurata;
c) è la misura di quanto, verosimilmente, la media campionaria è distante dalla
media della popolazione;
d) è proporzionale al numero delle osservazioni;
e) è più grande della deviazione standard stimata della popolazione.
Si tenga presente che la variabilità delle osservazioni è misurata dalla deviazione
standard, 𝑠. L’errore standard della media è 𝑠⁄√𝑛. Di conseguenza la sola risposta
corretta è la c)
Esercizio 3
I limiti di confidenza al 95% per la media stimati da un insieme di osservazioni
a) sono i limiti all’interno dei quali, sul lungo periodo, cadono il 95% delle
osservazioni;
b) sono i limiti all’interno dei quali la media campionaria cade con una
probabilità del 95%;
c) sono un modo per misurare la variabilità dell’insieme di osservazioni;
d) sono i limiti che dovrebbero contenere la media della popolazione nel 95% di
tutti i possibili campioni.
La risposta corretta è la d). I limiti di confidenza sono i valori estremi
dell’intervallo di confidenza. Non è corretto dire che la media della popolazione
cadrà entro l’intervallo di confidenza con una probabilità del 95%. La media di
una popolazione è un numero non è una variabile aleatoria e in quanto tale non
possiede una distribuzione di probabilità. E’ la probabilità che i limiti calcolati a
partire da un campione casuale contengano la media della popolazione ad essere
pari al 95%.
105
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Esercizio 4
In un periodo di epidemia influenzale, su 100 soggetti 70 sono affetti da influenza. Si
vuole calcolare l’intervallo di confidenza relativo alla proporzione 𝑝 della
popolazione al 95%.
In un campione casuale di 100 soggetti, 70 sono affetti da influenza. Quindi
𝑥
70
𝑝̂ = =
= 0.70
𝑛 100
è una stima puntuale di 𝑝. Risultando 𝑛𝑝̂ = 70 e 𝑛(1 − 𝑝̂ ) = 100 ∙ (1 − 0.70) = 30
la dimensione del campione è sufficientemente grande per giustificare l’uso
dell’approssimazione alla normale e quindi un intervallo di confidenza approssimato
al 95% per 𝑝 è
0.70(1 − 0.70)
0.70(1 − 0.70)
(0.70 − 1.96√
; 0.70 + 1.96√
100
100
oppure
(0.610; 0.790)
106
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Test statistici
Ipotesi statistica
Passiamo alla seconda grande classe di metodi di inferenza: la verifica di ipotesi
mediante test statistici.
Si è già detto che non sempre è possibile compiere rilevazioni di una determinata
caratteristica direttamente sull’universo perché, ad esempio, il collettivo è infinito.
Pertanto spesso si compiono rilevazioni parziali e si generalizzano le conclusioni,
raggiunte relativamente al campione, alla totalità della popolazione. In tale ottica ci si
domanda come è possibile estendere le conclusioni ricavate dalle unità osservate a
tutto il collettivo, ricercando e possibilmente massimizzando, i limiti di validità e di
attendibilità di tali generalizzazioni.
Per fare questa inferenza si formula una ipotesi sulla caratteristica della popolazione
in esame e successivamente si verifica la validità di tale ipotesi mediante un test
statistico. L’ipotesi formulata, viene indicata comunemente con 𝐻0 e viene chiamata
ipotesi nulla. Può riguardare il valore di un parametro della popolazione, per esempio
la media, la varianza, la frequenza relativa, la mediana e così via. In questi casi si
parla di ipotesi parametrica. Altrimenti si parla di ipotesi non parametrica, per
esempio l’ipotesi di esistenza o meno di una relazione statistica in una coppia di
fenomeni congiuntamente osservati sulla stessa popolazione, oppure sulle frequenze
cumulate ecc. La verifica di ipotesi è la metodologia inferenziale che , a partire dei
dati campionari, porta a decidere se accettare o rifiutare l’ipotesi nulla 𝐻0 ,
controllando probabilisticamente l’errore campionario. Il test statistico è la regola
pratica che porta a questa decisione.
Errore campionario e livello di significatività
Un test statistico, cioè la regola che porta ad accettare o rifiutare 𝐻0 è basato su dati
campionari, cioè su un’osservazione parziale dell’intera popolazione. E’ quindi
condotto in condizioni d’incertezza, quando il test porta ad un rifiuto di 𝐻0 non
107
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
significa necessariamente “𝐻0 falsa” ma solo che “ i dati campionari non suffragano
sufficientemente 𝐻0 ”. Quando invece il test porta all’accettazione di 𝐻0 , questo non
significa necessariamente “𝐻0 vera” ma solo che “ i dati campionari supportano 𝐻0 ".
Accettare o rifiutare 𝐻0 sulla base dei dati campionari comporta inevitabilmente il
rischio di commettere un errore.
Possiamo avere:
Errore di I specie. L’errato rifiuto, cioè sbagliare rifiutando 𝐻0 vera
Errore di II specie. Errore che si commette accettando 𝐻0 falsa
Per tenere conto di entrambi gli errori è necessaria una teoria più avanzata che
richiede più matematica e quindi va oltre i nostri scopi. Ci limiteremo a controllare
probabilisticamente l’errore di I specie. Con il test statistico si scegli a priori (quindi
si tiene sotto controllo) la probabilità di commettere un errore di I specie. Possiamo
sceglierla piccola quanto ci pare e quanto ci conviene ma non zero, perché il rischio
di errore esiste sempre ed è ineliminabile. Poiché questa probabilità è del tipo
probabilità di sbagliare, la indicheremo con il simbolo 𝛼
Verifica di ipotesi
Vediamo le fasi con cui si svolge la verifica di un’ipotesi.
1. Formulazione delle ipotesi . La prima fase consiste nell’enunciazione
dell’ipotesi statistica che si vuole sottoporre a verifica (ipotesi nulla 𝐻0 ). Si
chiama invece ipotesi alternativa o di ricerca , e si indica con 𝐻𝐴 l’ipotesi
contraria ad 𝐻0 . In genere l’ipotesi nulla pone l’assenza di relazioni
significative tra variabili a differenza di quella alternativa che ipotizza
l’esistenza di una relazione.
2. Distribuzione campionaria. La seconda fase riguarda l’individuazione della
distribuzione teorica di probabilità. Sappiamo infatti che la distribuzione
campionaria di una statistica ci consente di conoscere, dati certi requisiti, la
probabilità associata ai possibili valori che quella data statistica può assumere.
I requisiti richiesti variano a seconda del tipo di test adottato e riguardano
fondamentalmente la forma della distribuzione; un requisito però è comune a
tutti i test di cui ci occuperemo: quello riguardante la casualità e l’indipendenza
dei campioni. Le distribuzioni campionarie costituiscono i modelli di
riferimento ed è possibile utilizzare le loro caratteristiche e le loro proprietà
matematiche. La scelta di una particolare distribuzione piuttosto che di un’altra
dipende da parametri quali ad esempio il tipo di dati, la numerosità del
campione. La statistica campionaria ci fornisce le probabilità associate a tutti i
valori assumibili da una data variabile statistica, ma, nella verifica di una
determinata ipotesi siamo interessati alla probabilità di un solo risultato: quello
relativo al nostro campione. Prima di passare al calcolo del test e individuare la
sua possibilità di verificarsi, è necessario scegliere il livello di significatività.
108
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
3. Livelli di significatività. Tale livello con indicheremo come detto con la lettera
𝛼, si pone in genere uguale a 0.05, a 0.01 e più di rado a 0.001. Esso divide il
campo di esistenza della funzione test in due subaree, quella di rigetto e quella
di accettazione, delimitate dai valori critici. La prima è costituita da tutti quei
valori che hanno una bassissima probabilità di verificarsi se 𝐻0 è vera, la
seconda invece comprende quei valori che hanno una bassissima probabilità di
verificarsi se è vera l’ipotesi alternativa. Se il valore della statistica del nostro
campione sarà compreso nell’area di accettazione, si deciderà di accettare
l’ipotesi nulla, altrimenti si propenderà per l’accettazione di quella alternativa.
Un livello di significatività dello 0.01 ci indica, ad esempio, che la probabilità
di accettare l’ipotesi quando statisticamente è vera è dell’1% il che equivale a
dire che ci sono 99 probabilità su 100 di respingere 𝐻0 quando è falsa.
Scegliere un livello di significatività significa dunque stabilire il rischio di
commettere un errore rifiutando una ipotesi statisticamente vera. Quello che
occorre stabilire è il tipo di test che si vuole adottare: unidirezionale o
bidirezionale. Nel primo caso si otterrà una zona di rigetto in corrispondenza di
una coda della distribuzione e una zona di accettazione costituita dalla
rimanente porzione di area; nel secondo caso si otterranno invece due zone di
rifiuto in corrispondenza delle due code, e una di accettazione.
4. Calcolo del test e verifica delle ipotesi. In questa fase si procede al calcolo
della statistica nel campione e si decide se accettare o rigettare l’ipotesi nulla.
Se il valore del nostro campione cade nella regione di rifiuto significa che, se è
vera l’ipotesi nulla, la probabilità di ottenere i dati osservati è minore del
livello di significatività prefissato e possiamo sostenere- con una probabilità
stabilita dal livello di significatività 𝛼 di commettere un errore- che l’ipotesi
nulla è falsa e quindi rifiutarla.
La probabilità di ottenere i dati osservati o dati aventi una differenza ancora
maggiore rispetto al valore previsto dall’ipotesi nulla (nell’ipotesi che 𝐻0 sia
vera) è detto valore 𝑃 del test o semplicemente valore 𝑃. In conclusione per
accettare o rifiutare l’ipotesi nulla si confrontano due probabilità: il livello di
significatività e il valore 𝑃. Se il valore 𝑃 del test è minore o uguale al livello
di significatività , l’ipotesi nulla viene rifiutata; se viceversa è maggiore
l’ipotesi nulla non può essere rifiutata.
Vediamo alcuni esempi
Esempio 1
Z test per la verifica di ipotesi sulla media per popolazione normale con
varianza nota.
109
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Consideriamo la distribuzione dei livello di colesterolo sierico della popolazione
maschile di ipertesi e fumatori e assumiamo che la deviazione standard della
popolazione sia 𝜎 = 46 𝑚𝑔⁄100𝑚𝐿. Vogliamo verificare l’ipotesi che il livello
medio 𝜇 di colesterolo di questa popolazione sia uguale a quello dei soggetti maschi
di età compresa tra 20 e 74 anni. Abbiamo già visto che quest’ultima popolazione ha
un livello medio di colesterolo sierico pari a 𝜇0 = 211 𝑚𝑔⁄100𝑚𝐿. L’ipotesi nulla
da testare è quindi
𝐻0 : 𝜇 = 𝜇0 = 211 𝑚𝑔⁄100𝑚𝐿
Poiché la media della popolazione di ipertesi fumatori può essere minore o maggiore
di 𝜇0 , siamo interessati alle deviazioni che si verificano in entrambe le direzioni.
Quindi eseguiremo un test bilaterale. L’ipotesi alternativa per il test bilaterale è
𝐻𝐴 : 𝜇 ≠ 211 𝑚𝑔⁄100𝑚𝐿
Fissiamo il livello di significatività. Ad esempio sia
𝛼 = 0.05
Utilizziamo il campione casuale già indicato in precedenza costituito da 12 ipertesi
fumatori con livello medio di colesterolo sierico 𝑥̅ = 217 𝑚𝑔⁄100𝑚𝐿.
E’ verosimile che questo campione derivi da una popolazione con media
211𝑚𝑔⁄100𝑚𝐿? Per rispondere a questa domanda eseguiamo il test statistico. In
accordo con le già viste proprietà della distribuzione campionaria della media
possiamo dire che
𝑋̅ − 𝜇0
𝑍=
𝜎
√𝑛
ha una distribuzione approssimativamente normale standardizzata. Poiché questo test
si basa su questa distribuzione, viene denominato test z.
Fatte queste premesse eseguiamo il test statistico. Si ha
217 − 211
𝑧=
= 0.45
46
√12
Per rifiutare o non rifiutare l’ipotesi nulla, dobbiamo confrontare il valore
sperimentale del test con i valori critici. Non si accetta 𝐻0 se
𝑧 ≤ −1.96
𝑜𝑝𝑝𝑢𝑟𝑒
𝑧 ≥ 1.96
Nel caso in esame 𝑧 ≤ 1.96 e di conseguenza accettiamo o meglio non rifiutiamo
l’ipotesi 𝐻0 . In base a questo campione non abbiamo sufficiente evidenza per
concludere che il livello medio di colesterolo sierico della popolazione di ipertesi
fumatori sia diverso da 211𝑚𝑔⁄100𝑚𝐿.
Esempio 2
t- test per la verifica di ipotesi sulla media per popolazione normale con
varianza ignota
110
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Si consideri un campione casuale di 10 bambini selezionata dalla popolazione di
neonati che assumono antiacidi contenenti alluminio. La distribuzione dei livelli di
alluminio plasmatico di questa popolazione è approssimativamente normale con
media 𝜇 e deviazione standard 𝜎 non note. Il livello medio 𝑥̅ di alluminio plasmatico
del campione di 10 neonati e la sua deviazione standard 𝑠 sono rispettivamente
𝑥̅ = 37.20 𝜇𝑔⁄𝐿
𝑠 = 7.13 𝜇𝑔⁄𝐿
Sappiamo inoltre che il livello medio di alluminio plasmatico della popolazione di
neonati che non assumono antiacidi è 𝜇0 = 4.13 𝜇𝑔⁄𝐿. E’ verosimile che i dati del
nostro campione provengano da una popolazione con media 𝜇0 ?
Per rispondere a questa domanda eseguiamo un test di ipotesi. L’ipotesi nulla è
𝐻0 : 𝜇 = 𝜇0 = 4.13 𝜇𝑔⁄𝐿
e l’ipotesi alternativa è
𝐻𝐴 : 𝜇 ≠ 4.13 𝜇𝑔⁄𝐿
Siamo interessati alle deviazioni dalla media in entrambe le direzioni e vogliamo
sapere se 𝜇 è maggiore o minore di 4.13. Pertanto eseguiamo un test bilaterale. Ad un
livello di significatività 𝛼 = 0.05.
Poiché non conosciamo la deviazione standard 𝜎 della popolazione, utilizziamo la
variabile casuale t ossia eseguiamo un test t. Il test statistico è quindi
𝑥̅ − 𝜇0
𝑡=
𝑠
√𝑛
ossia
37.20 − 4.13
= 14.67
7.13
√10
Se l’ipotesi nulla è vera, questo risultato ha una distribuzione t con 10 − 1 = 9 gradi
li libertà.
𝑡=
Dobbiamo ora calcolare i valori critici Guardando la tabella allegata individuiamo
prima la colonna corrispondente al livello di significatività d’interesse (nel nostro
caso 𝛼 = 5% complessivamente su entrambe le code ossia 0.025 su ogni code) e
successivamente troviamo la riga corrispondente al numero di gradi di libertà (nel
nostro caso 𝑔𝑙 = 9). Il numero della cella corrispondente è il valore critico. Nel
nostro caso 𝑡𝑐 = 2.2622 che è minore del valore sperimentale e quindi rifiutiamo
l’ipotesi nulla. Questo campione di neonati fornisce sufficiente evidenza che il livello
medio di alluminio plasmatico dei bambini che assumono antiacidi non è uguale a
quello dei bambini che non ne assumono.
Esempio 3
Z test per grandi campioni per la verifica di ipotesi sulla frequenza relativa
p
111
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
La distribuzione della sopravvivenza a 5 anni dei pazienti al di sotto di 40 anni ai
quali è stato diagnosticato un cancro al polmone ha una proporzione della
popolazione p non nota. Sappiamo tuttavia che la proporzione di pazienti che
sopravvive a 5 anni tra quelli oltre i 40 anni al momento della diagnosi è dell’8.2%.
E’ possibile che anche nella popolazione di pazienti al di sotto di 40 anni la
proporzione di sopravvivenza sia 0.082? Per verificarlo facciamo un test statistico.
Formuliamo un’ipotesi sul valore p della proporzione della popolazione. Poiché il
nostro obiettivo è di verificare se la proporzione di pazienti con cancro del polmone
che sopravvive almeno 5 anni dopo la diagnosi è la stessa tra i pazienti al di sotto e
oltre i 40 anni , l’ipotesi nulla è:
𝐻0 : 𝑝 = 𝑝0 = 0.082
Facciamo un test bilaterale e quindi l’ipotesi alternativa è:
𝐻𝐴 : 𝑝 ≠ 0.082
Scegliamo come livello di significatività un valore 𝛼 = 5%.
Selezioniamo poi un campione casuale di osservazioni dicotomiche dalla popolazione
originaria e calcoliamo la probabilità di osservare una proporzione campionaria pari
o più estrema di 𝑝̂ , nell’ipotesi che la proporzione della popolazione sia p. In altre
parole calcoliamo il test statistico
𝑝̂ − 𝑝
𝑧=
√𝑝(1 − 𝑝)
𝑛
Se 𝑛 è sufficientemente grande e l’ipotesi nulla è vera, questo rapporto è distribuito
normalmente con media 0 e deviazione standard 1.
Per un campione casuale di 52 pazienti al di sotto di 40 anni ai quali è stato
diagnosticato un cancro al polmone, si è trovato 𝑝̂ = 0.115. Pertanto il test statistico
è.
𝑝̂ − 𝑝
0.115 − 0.082
𝑧=
=
= 0.87
0.082(1
−
0.082)
𝑝(1
−
𝑝)
√
√
𝑛
52
Non si accetta 𝐻0 se
𝑧 ≤ −1.96
𝑜𝑝𝑝𝑢𝑟𝑒
𝑧 ≥ 1.96
Nel caso in esame 𝑧 = 0.87 ≤ 1.96 e quindi non rifiutiamo l’ipotesi nulla.
Test a una coda
Le ipotesi fatte finora erano tutte bilaterali. Un test statistico per la verifica di ipotesi
bilaterale ha la regione critica formata da due zone sotto le due code della
distribuzione campionaria, ciascuna con probabilità 𝛼⁄2. Chiameremo questo tipo di
test, come si usa, a due code.
Nella pratica sono anche utili ipotesi unilaterali, cioè l’ipotesi nulla del tipo :
𝐻0 : 𝜇 ≤ 𝜇0 oppure 𝐻0 : 𝜇 ≥ 𝜇0
112
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Per verificare ipotesi nulle unilaterali si pone la regione critica sotto un’unica coda e
si esegue un test ad una coda. Per verificare l’ipotesi 𝐻0 : 𝜇 ≤ 𝜇0 si pone la regione
critica tutta sotto una coda di destra mentre la coda di sinistra fa parte della zona di
accettazione. Inoltre non sarà più necessario, come facevamo per il test a due code,
dividere la probabilità di sbagliare in 𝛼⁄2 sotto una coda e 𝛼⁄2 sotto l’altra: in un
test a una coda la regione critica è composta da una sola coda di probabilità 𝛼.
Quando l’ipotesi unilaterale è del tipo 𝐻0 : 𝜇 ≥ 𝜇0 , si ribalta il ragionamento.
Naturalmente il test ad una coda porta ad un cambiamento del valore critico rispetto
ad un test a due code. Per esempio 𝛼 = 5% su una coda 𝑧𝑐 = ±1.96.
Concetto di p-value
Di solito le analisi statistiche si fanno con il computer il quale esegue il test
producendo un unico numero con il quale possiamo decidere se accettare o rifiutare
𝐻0 , qualunque sia il livello di significatività che vogliamo fissare. Tale valore viene
chiamato p-value o significatività empirica del test.
Il p-value è una probabilità ed dunque un numero compreso tra 0 e 1. Rappresenta la
probabilità di ottenere i dati osservati o di ottenere dati ancora meno in accordo con
l’ipotesi nulla, supposta vera.
Come si usa? Se il p-value risulta più piccolo del livello prescelto 𝛼 (per un test a una
coda) o di 𝛼⁄2 per un test a due code, allora si rifiuta 𝐻0 .
Il computer fornisce il p-value in sostituzione del valore critico. Il valore critico
dipende sempre dall’ 𝛼 scelto ed è diverso per diversi livelli di significatività. Il pvalue invece di pende solo dal valore sperimentale del test, cioè dai dati campionari e
dunque rimane sempre lo stesso a qualunque livello di significatività.
Quando si esegue un test “a mano”, si decide se accettare o rifiutare 𝐻0 confrontando
i due valori: quello sperimentale e quello critico. Viceversa quando si esegue il test al
computer, si decide se accettare o rifiutare 𝐻0 confrontando due probabilità: il pvalue (fornito dal computer) e il livello 𝛼 o 𝛼⁄2 (scelto da noi). Le due procedure
sono equivalenti cioè portano allo stesso risultato.
Dati campionari qualitativi bivariati: tabelle di contingenza.
Abbiamo già descritto una coppia di fenomeni congiuntamente rilevati sulla stessa
popolazione. Ora abbiamo l’obiettivo di inferenziarli.
Abbiamo già visto anche che si ha 𝜒 2 = 0 se e sole se X ed Y sono statisticamente
indipendenti; se invece X ed Y sono connessi, l’indice 𝜒 2 risulterà maggiore di 0 e,
una volta normalizzato, fornisce una misura dell’intensità di questa connessione.
̂2 calcolato sulla tabella di contingenza è
Quando i dati sono campionari, l’indice 𝜒
allora una stima della reale ma ignota connessione esistente tra X e Y sull’intera
popolazione (per questo motivo abbiamo messo il simbolo con il cappello).
113
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
̂2 , per n
Ora un teorema della teoria della probabilità garantisce che 𝜒
sufficientemente grande è approssimativamente una variabile casuale chiamata anche
lei chi quadro con gradi di libertà (k-1)(h-1) (k, numero righe, h, numero colonne
della tabella di contingenza con i dati campionari) e può essere utilizzata come
statistica test nella verifica di ipotesi.
Variabile casuale Chi quadro
E’ una variabile casuale continua che assume valori positivi. Ha un solo parametro, ci
gradi di libertà, e anche per tale variabile esistono le tavole.
Test Chi quadro di indipendenza statistica
L’ipotesi nulla che esprime in formule che X ed Y sono indipendenti è
𝐻0 : 𝜒 2 = 0
Per eseguire il test statistico eseguiamo la solita procedura.
Bisogna osservare che si tratta di un test a una coda con la regione critica tutta sotto
la coda di destra. Si tratta anche di un test approssimato per grandi campioni
applicabile cioè se n è sufficientemente grande. L’unico valore critico si va a cercare
sulle tavole del 𝜒 2 con (k-1)(h-1) gradi di libertà. Infine si rifiuta 𝐻0 : 𝜒 2 = 0 se il
̂2 ≥valore critico.
valore sperimentale cade nella regione di rifiuto cioè se 𝜒
Esempio
Consideriamo due variabili casuali dicotomiche. Si consideri ad esempio la tabella
2 × 2 che illustra i risultati di uno studio sull’efficacia dei caschi protettivi per
bicicletta(variabile Y) nella prevenzione dei traumi cranici (variabile X).
Casco protettivo Totale
Trauma cranico
SI
NO
SI
17
218
235
114
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
NO
130
428
558
Totale
147
646
793
Dei 793 soggetti coinvolti in incidenti con la bicicletta, 147 indossavano il casco
protettivo al momento dell’incidente e 646 no. Tra coloro che indossavano il casco
protettivo, 17 riportarono traumi cranici che richiesero assistenza sanitaria e 130 no.
Tra coloro che non indossavano il casco , 218 soggetti riportarono traumi cranici e
428 no. I numeri all’interno della tabella – 17, 130, 218 e 428- sono le frequenze
osservate in ciascuna combinazione delle due categorie.
Ipotesi nulla 𝐻0 : la proporzione di soggetti che hanno riportato traumi cranici tra
coloro che indossavano il casco protettivo al momento dell’incidente è uguale alla
proporzione di soggetti che hanno riportato traumi cranici che non indossavano il
casco (in altre parole non vi è nessuna associazione tra le variabili).
𝐻0 : 𝜒 2 = 0
L’ipotesi alternativa è:
𝐻𝐴 : la proporzione di soggetti che hanno riportato traumi cranici non sono uguali
nelle due popolazioni (ossia tra le due variabili vi è un’associazione di un qualche
tipo)
Eseguiamo il test a livello di significatività del 5%.
Calcoliamo le frequenze attese per ciascuna cella della tabella di contingenza
nell’ipotesi che sia vera l’ipotesi nulla.
In generale la frequenza attesa per una determinata cella della tabella è uguale al
totale di riga moltiplicato per il totale di colonna diviso il totale della tabella
Le frequenze attese sono quindi:
Trauma cranico Casco protettivo
Totale
SI
NO
235 × 147
SI
191.4 235
= 43.6
793
NO
103.6
454.6 558
Totale
147
646
793
Il test chi quadro confronta le frequenze osservate in ciascuna categoria della tabella
di contingenza con le corrispondenti frequenze attese e viene utilizzato per stabilire
se le differenze tra le frequenze osservate e quelle attese siano troppo grandi per
essere attribuite al caso. Si calcola con la seguente somma
(𝑜𝑠𝑠𝑒𝑟𝑣𝑎𝑡𝑜𝑖 − 𝑎𝑡𝑡𝑒𝑠𝑜𝑖 )2
2
̂
𝜒 =∑
𝑎𝑡𝑡𝑒𝑠𝑜𝑖
𝑖
ove 𝑜𝑠𝑠𝑒𝑟𝑣𝑎𝑡𝑜𝑖 è la frequenza di individui osservata nella i-esima categoria e
𝑎𝑡𝑡𝑒𝑠𝑜𝑖 è la frequenza attesa in quella categoria sotto l’ipotesi nulla. Si osservi che la
statistica 𝜒 2 utilizza le frequenza assolute osservate ed attese e non le proporzioni
115
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
(che sono le frequenze relative). Si osservi anche che se le frequenze osservate
fossero esattamente uguali alle frequenze attese sotto l’ipotesi nulla, 𝜒 2
sarebbe 0. Maggiore è 𝜒 2 maggiore è la discrepanza tra le frequenze osservate e le
frequenze attese sotto l’ipotesi nulla.
Eseguiamo il test:
(17 − 43.6)2 (130 − 103.6)2 (218 − 191.4)2 (428 − 454.6)2
2
̂=
𝜒
+
+
+
43.6
103.4
191.4
454.6
Eseguendo i calcoli si ottiene
𝜒 2 = 16.228 + 6.843 + 3.697 + 1.556 = 28.324
La distribuzione teorica 𝜒 2
La distribuzione teorica 𝜒 2 è in realtà una famiglia di distribuzioni perché dipende
dal numero di gradi di libertà come si vede dal grafico sottostante. Per questa
distribuzione i gradi di libertà si calcolano in questo modo:
𝑔𝑙 = (𝑛𝑢𝑚𝑒𝑟𝑜 𝑑𝑖 𝑟𝑖𝑔ℎ𝑒 − 1) × (𝑛𝑢𝑚𝑒𝑟𝑜 𝑑𝑖 𝑐𝑜𝑙𝑜𝑛𝑛𝑒 − 1)
Le sue caratteristiche essenziali sono state tabulate in tavole statistiche di semplice
utilizzo.
A questo punto dobbiamo calcolare il valore critico. Guardando la tabella allegata
individuiamo prima la colonna corrispondente al livello di significatività d’interesse
116
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
(nel nostro caso 𝛼 = 5%) e successivamente troviamo la riga corrispondente al
numero di gradi di libertà (nel nostro caso 𝑔𝑙 = (2 − 1) × (2 − 1) = 1). Il numero
della cella corrispondente è il valore critico. Nel nostro caso
𝜒𝑐2 = 3.84
̂2 (28.324) è maggiore di 3.83 rifiutiamo l’ipotesi nulla
Poiché il valore osservato di 𝜒
e concludiamo che X ed Y non sono indipendenti.
Esercizi
Esercizio 1
E’ stata condotta una sperimentazione clinica per verificare se un nuovo trattamento
influisca sul tasso di recupero di pazienti affetti da una malattia debilitante. L’ipotesi
nulla 𝐻0 : il trattamento è inefficace è stata rifiutata con un valore di P pari a 0.04. I
ricercatori hanno usato un livello di significatività del 5%. Dite se ciascuna delle
seguenti conclusioni è corretta e se non lo è spiegate perché.
a) il trattamento ha solo un piccolo effetto
b) il trattamento ha qualche effetto
c) la probabilità di commettere un errore di tipo I è 0.04
d) l’ipotesi nulla non sarebbe stata rifiutata se il livello di significatività fosse
stato 0.01.
Risposte a) non corretto. Il valore P non dà l’entità dell’effetto. b) corretto. 𝐻0 è stata
rifiutata, quindi concludiamo che vi è stato realmente un effetto. c) non corretto. La
probabilità di commettere un errore di tipo I è stabilità dal livello di significatività,
0.05, che è deciso anticipatamente. d) Corretto
Esercizio 2
Una casa farmaceutica dichiara che una dose di un certo farmaco ha effetto dopo 25
minuti dall’assunzione e che tale tempo ha una distribuzione normale con varianza 49
min2. Su un campione casuale di 25 persone si è osservato un tempo medio fra
l’assunzione e l’effetto di 30 minuti. Verificare se l’affermazione della casa
farmaceutica è vera a livello di significatività del 5%.
Supponiamo che la casa farmaceutica dichiari il vero. Di conseguenza il valor medio
del tempo che intercorre tra l’assunzione e l’effetto è di 25 min e il campione in
esame è stato estratto da questa popolazione. Quindi
𝐻0 : 𝜇 = 𝜇0
Come ipotesi alternativa poniamo
𝐻𝐴 : 𝜇 ≠ 𝜇0
Il test è quindi bilaterale. Essendo 𝛼 = 5% i valori critici sono 𝑧𝑐 = ±1.96.
Eseguendo il test si ottiene:
117
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
𝑥̅ − 𝜇0
30 − 25
5
=
=
5
×
= 3.57
𝜎
7
√49
√𝑛
√25
Essendo 3.57 > 1.96 si rifiuta l’ipotesi nulla ossia il tempo che intercorre tra
l’assunzione del farmaco e il suo effetto non è di 25 minuti.
𝑧=
Esercizio 3
In occasione delle ultime elezioni amministrative il partito A ha ottenuto una
percentuale di voti pari al 30%. In vista delle prossime elezioni, per stabilire se si è
verificata una perdita nelle preferenze per il partito A, si estrae un campione
bernoulliano di n=100 elettori ottenendo una percentuale di preferenze per A pari al
20%. Stabilire se, a livello di significatività del 5%, lo scarto osservato tra la
percentuale delle ultime elezioni e quella del campione può essere considerata
casuale o è invece una perdita di consensi.
Supponiamo che lo scarto osservato tra la percentuale delle ultime elezioni e quella
del campione sia casuale. In questo caso il campione di 100 elettori è stato estratto da
una popolazione con frequenza attesa 𝑝0 = 0.30. Inoltre l’ipotesi alternativa sia che
lo scarto sia solo una perdita di consensi ossia avvenga in una sola direzione.
Di conseguenza si ha
𝐻0 : 𝑝 = 𝑝0
𝐻𝐴 : 𝑝 < 𝑝0
Il test è unilaterale e la statistica test è
𝑝 − 𝑝0
0.20 − 0.30
𝑧=
=
= −0.218
(1
)
0.30
×
0.70
𝑝
−
𝑝
0
√ 0
√
100
𝑛
Il valore critico per un test unilaterale con 𝛼 = 5% è 𝑧𝑐 = −1.65. Essendo
−0.218 > −1.65 si accetta l’ipotesi nulla ossia si ritiene che la differenza osservata
sia casuale e non da indicare una riduzione significativa dei consensi.
Esercizio 4
Un istituto scolastico effettua un’indagine per analizzare l’eventuale relazione tra il
genere X e il rendimento scolastico Y. Viene estratto un campione bernoulliano di
110 studenti e i dati sono sintetizzati nella seguente tabella
Y: media dei voti 4-6 6-8 8-10
X: genere
F
9
16 25
50
M
20 35 5
60
29 51 30
110
Verificare con un opportuno test a livello di significatività del 5% se nella
popolazione d’interesse esiste una significativa relazione statistica tra i fenomeni.
118
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
Ipotesi nulla 𝐻0 : non vi è nessuna associazione tra le variabili. quindi
𝐻0 : 𝜒 2 = 0
L’ipotesi alternativa è:
𝐻𝐴 : tra le due variabili vi è un’associazione di un qualche tipo
Eseguiamo il test a livello di significatività del 5%.
Calcoliamo le frequenze attese per ciascuna cella della tabella di contingenza
nell’ipotesi che sia vera l’ipotesi nulla.
Y: media dei voti 4-6
X: genere
F
6-8
8-10
50 × 29
23.18 13.64 50
= 13.18
110
15.82
27.82 16.36 60
29
51
30
110
M
Dai dati forniti si ottiene il seguente valore sperimentale
3
2
̂2 = ∑ ∑
𝜒
𝑖=1 𝑗=1
(9 − 13.18)2 (16 − 23.18)2
(5 − 16.36)2
+
+⋯+
= 23.87
13.18
23.18
16.36
Il valore critico si ricava dalle tavole tenendo presente che (h-1)(k-1)=2∙1=2 gradi di
libertà ed 𝛼 = 0.05. Si ottiene 𝜒𝑐2 = 5.99.
Essendo 23.87 > 5.99 si rifiuta l’ipotesi di indipendenza fra media dei voti e genere
nella popolazione di interesse a livello di significatività del 5% ovvero esiste una
relazione significativa tra i due fenomeni.
119
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
120
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
121
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
122
Appunti di
“Metodologia Statistica Applicata in Ambito Biomedico e Clinico”
Prof. Claudio Baraldi – A.A. 2015/16
123