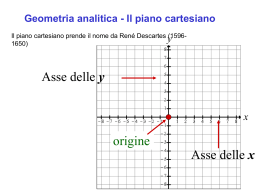
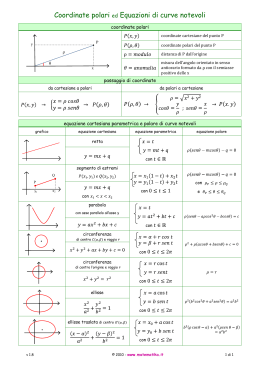
Elaborati
per il corso
ELEMENTI DI TOPOGRAFIA
Prof. Renzo Carlucci
Elaborati svolti da
TOSCANO SIMONE
matricola: 281791
Anno Accademico 2006/2007
Sessione di esame
Novembre 2006
Indice
Ö ESERCITAZIONE SU ANGOLI E CONVERSIONI ANGOLARI ……………pag. 3
Ö ESERCITAZIONE DI CARTOGRAFIA ……………………………………..……..pag. 7
o
o
o
o
o
o
o
Scelta della carta ………………………………………………………………………pag. 7
Scelta dei punti trigonometrici ……………………………….…………………….pag. 10
Calcolo delle coordinate cartesiane dei due punti ………….……………………pag. 11
Calcolo delle coordinate geografiche dei due punti ………….…………………..pag. 15
Calcolo della distanza tra i due punti trigonometrici …………………………..pag. 17
Calcolo angolo di direzione (AB) – Direzione alla bussola ……………………..pag. 19
Calcolo del dislivello tra i due punti trigonometrici …………………………….pag. 21
Ö RILIEVO TOPOGRAFICO DI UNA STANZA ……………..……………………pag. 22
Ö FOTOGRAMMETRIA …………………………………………………………………pag. 27
o
Fotogrammetria digitale …………………………………………………………….pag. 32
Ö ESERCITAZIONE DI AEROFOTOGRAMMETRIA …………………………...pag. 35
2
ESERCITAZIONE SU ANGOLI E
CONVERSIONI ANGOLARI
Esercizio n. 1
eseguire le seguenti operazioni
132 ° 32 ' 47.900 '' + 29 ° 37 ' 53.200 '' = 162 ° 10 ' 41.100 ''
344 ° 15 ' 12.300 '' - 175 ° 48 ' 29.600 '' = 168 ° 26 ' 42.700 ''
79 ° 8 ' 5.400 '' - 112 ° 23 ' 56.400 '' + 360 ° = 326 ° 44 ' 9.000 ''
189 ° 48 ' 48.350 '' x 2 - 136 ° 36 ' 47.399 '' - 360 ° = 19 ° 37 ' 10.000 ''
Esercizio n. 2
trasfomare i seguenti angoli nei vari sistemi
DEG GRAD RAD
301 ° 43 ' 21.505 '' 301.7226403 335.2473781 5.2660535
7 ° 14 ' 12.810 '' 7.2368917 8.0409907 0.1263076
245 ° 15 ' 35.201 '' 245.2597781 272.5108645 4.2805906
136 ° 36 ' 47.399 '' 136.6131664 151.7924071 2.3843496
299 ° 26 ' 47.640 '' 299.4465666 332.7184074 5.2263285
DMS
Esercizio 3:
In un poligono irregolare di 5 lati ABCDE, si conoscono 4 angoli interni
ABC = 154°35’49.7”
BCD = 70g 88c 41.6cc
CDE = 141.75482 gon
DEA = 1.507865 rad
Determinare il valore del quinto angolo EAB espresso in gradi
sessagesimali, gradi centesimali e radianti
[107°38’0.52” ; 119.592754 gon ; 1.87855859 rad]
3
4
5
6
ESERCITAZIONE DI CARTOGRAFIA
Determinare analiticamente su una tavoletta I.G.M. in scala 1:25000 la distanza, il
dislivello e la direzione alla bussola tra due punti trigonometrici liberamente scelti.
Dei punti trigonometrici scelti fornire le coordinate cartesiane e geografiche nel sistema
di riferimento presente sulla carta.
Ö
SCELTA DELLA CARTA
Come carta è stata scelta la seguente:
CARTA D’ITALIA - SCALA 1 : 25 000
FOGLIO N° 388 SEZ. IV - GENZANO DI ROMA
7
La carta rappresenta la zona di Genzano di Roma in scala 1 : 25 000, zona appartenente
al Fuso 33, con reticolo di riferimento UTM-WGS84. Come riportato a bordo del foglio, le
coordinate ai vertici della carta sono:
8
9
Ö
SCELTA DEI PUNTI TRIGONOMETRICI
I punti trigonometrici da me scelti sono
MONTE CAVO (A)
MASCHIO DELL’ARTEMISIO (B).
10
Ö
CALCOLO DELLE COORDINATE CARTESIANE DEI DUE PUNTI
Per il calcolo analitico delle coordinate cartesiane dei due punti, bisogna misurare la
distanza dalle linee del reticolo di riferimento immediatamente ad ovest ed a sud dei
punti.
Sapendo che un riquadro misura 4 cm di lato sulla carta (che in scala 1 : 25 000
equivalgono a 1000 m nella realtà) si può impostare la seguente proporzione:
4 cm : 1000 m = (distanza misurata in cm sulla carta) : X
Il valore così ottenuto andrà aggiunto alla coordinata di riferimento riportata sul reticolo
(il valore va aggiunto poiché sono state prese come riferimento le linee immediatamente
a sud ed a ovest dei punti trigonometrici).
Punto trigonometrico Monte Cavo
Coordinata cartesiana est (x) in UTM-WGS84
Coordinata di partenza: 309.000 m
4 cm : 1000 m = 2,25 cm : X
´
X = 562,5 m
309.000 m + 562,5 m = 309.562,5 m coordinata cartesiana est Monte Cavo
11
Coordinata cartesiana nord (y) in UTM-WGS84
Coordinata di partenza: 4.624.000 m
4 cm : 1000 m = 2,95 cm : X
´
X = 737,5 m
4.624.000 m + 737,5 m = 4.624.737,5 m coordinata cartesiana nord Monte Cavo
Punto trigonometrico Maschio dell’Artemisio
Coordinata cartesiana est (x) in UTM-WGS84
Coordinata di partenza: 313.000 m
4 cm : 1000 m = 0,45 cm : X
´
X = 112,5 m
313.000 m + 112,5 m = 313.112,5 m coordinata cartesiana est Maschio dell’Artemisio
Coordinata cartesiana nord (y) in UTM-WGS84
Coordinata di partenza: 4.620.000 m
4 cm : 1000 m = 1,15 cm : X
´
X = 287,5 m
4.620.000 m + 287,5 m = 4.620.287,5 m coordinata cartesiana nord Maschio dell’Artemisio
12
Le coordinate cartesiane appena trovate si riferiscono al reticolato UTM-WGS84. Seguendo
le indicazioni riportate nella tabella riportata sulla tavola
Posso riportare le coordinate cartesiane dei due punti trigonometrici in riferimento al
sistema UTM-ED50 e GAUSS-BOAGA.
Supponiamo per esempio di volerle riportare da UTM-WGS84 a UTM-ED50.
I punti si trovano nel Fuso 33. Andremo così ad aggiungere alle coordinate est 70 m,
mentre alle coordinate nord 193 m.
Punto trigonometrico Monte Cavo
Coordinata cartesiana est (x) da UTM-WGS84 a UTM-ED50
309.562,5 m + 70 m = 309.632,5 m coordinata cartesiana est Monte Cavo
Coordinata cartesiana nord (y) da UTM-WGS84 a UTM-ED50
4.624.737,5 m + 193 m = 4.624.930,5 m coordinata cartesiana nord Monte Cavo
Punto trigonometrico Maschio dell’Artemisio
Coordinata cartesiana est (x) da UTM-WGS84 a UTM-ED50
313.112,5 m + 70 m = 313.182,5 m coordinata cartesiana est Maschio dell’Artemisio
Coordinata cartesiana nord (y) da UTM-WGS84 a UTM-ED50
4.620.287,5 m + 193 m = 4.620.480,5 m coordinata cartesiana nord Maschio dell’Artemisio
13
Calcolate le coordinate cartesiane dei punti trigonometrici sia nel sistema UTM-WGS84
che UTM-ED50, posso ricavare la designazione dei due punti trigonometrici seguendo
l’esempio riportato nella tavola I.G.M.
Designazione dei punti trigonometrici:
DESIGNAZIONE DI ZONA
NOME DEL PUNTO: U MONTE CAVO 949 m
Il particolare in coordinate UTM-WGS84 e UTM-ED50 è individuato
dal complesso dei seguenti valori:
33T
UTM-WGS84
UTM-ED50
Fuso:
33
33
Zona:
T
T
Quadrato di 100 km:
UG
UG
Coordinata est:
0956
0963
Coordinata nord:
2473
2493
DESIGNAZIONE:
33TUG09562473 33TUG09632493
Nella designazione del punto, misurare in decametri, con un
coordinatometro, le distanze dalla quadrettatura chilometrica a
partire dalle linee immediatamente ad ovest e a sud dal particolare
e registrare le coordinate trascurando le cifre scritte in carattere
piccolo lungo la cornice.
Identificazione del quadrato
di 100 km di lato:
UG
DESIGNAZIONE DI ZONA
NOME DEL PUNTO: UMASCHIO DELL’ARTEMISIO 812 m
Il particolare in coordinate UTM-WGS84 e UTM-ED50 è individuato
dal complesso dei seguenti valori:
33T
UTM-WGS84
UTM-ED50
Fuso:
33
33
Zona:
T
T
Quadrato di 100 km:
UG
UG
Coordinata est:
1311
1318
Coordinata nord:
2028
2048
DESIGNAZIONE:
33TUG13112028 33TUG13182048
Nella designazione del punto, misurare in decametri, con un
coordinatometro, le distanze dalla quadrettatura chilometrica a
partire dalle linee immediatamente ad ovest e a sud dal particolare
e registrare le coordinate trascurando le cifre scritte in carattere
piccolo lungo la cornice.
Identificazione del quadrato
di 100 km di lato:
UG
Nella designazione del punto, misurare in decametri, con un coordinatometro, le distanze
dalla quadrettatura chilometrica a partire dalle linee immediatamente ad ovest e a sud
dal particolare e registrare le coordinate trascurando le cifre scritte in carattere piccolo
lungo la cornice.
Ö
CALCOLO DELLE COORDINATE GEOGRAFICHE DEI DUE PUNTI
14
Per calcolare le coordinate geografiche dei due punti trigonometrici il procedimento da
seguire è analogo a quello per calcolare le coordinate geografiche. Ci si riferisce alla
squadratura posta ai bordi della carta, dove vengono indicati i valori di latitudine e
longitudine. Basta misurare le distanze dei punti dalle linee di latitudine e longitudine
immediatamente ad ovest ed a nord del punto e poi impostare le seguenti proporzioni:
Latitudine
7,4 cm sulla carta = 0° 01’ 00”
7,4 cm : 0° 01’ 00” = (distanza misurata sulla carta) : X
Longitudine
5,55 cm sulla carta = 0° 01’ 00”
5,5 cm : 0° 01’ 00” = (distanza misurata sulla carta) : X
Il valore così ottenuto andrà aggiunto alla coordinata di riferimento riportata sul bordo
della carta (il valore va aggiunto poiché sono state prese come riferimento le coordinate
immediatamente a sud ed a ovest dei punti trigonometrici).
Punto trigonometrico Monte Cavo
Coordinata geografica latitudine nord
Coordinata di partenza: 41° 45’ 00”
7,4 cm : 0° 01’ 00” = 0,7 cm : X ´
X = 0° 00’ 5,68”
41° 45’ 00” + 0° 00’ 5,68” = 41° 45’ 5,68” latitudine nord Monte Cavo
Coordinata geografica longitudine est
Coordinata di partenza: 12° 42’ 00”
5,55 cm : 0° 01’ 00” = 3,15 cm : X
´
X = 0° 00’ 34,36”
12° 42’ 00” + 0° 00’ 34,36” = 12° 42’ 34,36” longitudine est Monte Cavo
15
Punto trigonometrico Maschio dell’Artemisio
Coordinata geografica latitudine nord
Coordinata di partenza: 41° 42’ 00”
7,4 cm : 0° 01’ 00” = 5,5 cm : X ´
X = 0° 00’ 44,59”
41° 42’ 00” + 0° 00’ 44,59” = 41° 42’ 44,59” latitudine nord Maschio dell’Artemisio
Coordinata geografica longitudine est
Coordinata di partenza: 12° 45’ 00”
5,55 cm : 0° 01’ 00” = 1,19 cm : X
´
X = 0° 00’ 12,98”
12° 45’ 00” + 0° 00’ 12,98” = 12° 45’ 12,98” longitudine est Maschio dell’Artemisio
16
Ö
CALCOLO DELLA DISTANZA TRA I DUE PUNTI TRIGONOMETRICI
Usando le coordinate cartesiane in UTM-WGS84 dei due punti trigonometrici, si può
calcolare la distanza tra i due punti con la formula
(X
B
- X A )2 + (YB - YA )2
(313.112,5m - 309.562,5m )2 + (4.620.287,5m - 4.624.737,5m)2 = 5.692,54m
17
La distanza ottenuta va corretta del modulo di deformazione lineare che è riportato sulla
tavola I.G.M. nella seguente tabella
Modulo di deformazione lineare : 1,00003 m
Per tanto, la distanza corretta sarà:
5.692,54m
= 5.692,37 m distanza tra i punti trigonometrici A e B
1,00003m
Come verifica approssimativa dell’esattezza della distanza, basta misurare sulla carta la
distanza in centimetri tra i punti ed impostare la seguente proporzione:
1 cm : 250 m = (distanza misurata sulla carta) : X
Nel nostro caso abbiamo che la distanza in centimetri sulla carta tra un punto e l’altro è
di 22,77 cm. La proporzione sarà:
1 cm : 250 m = 22,77 cm : X
´
X = 5.692,5 m
Il valore ottenuto si avvicina molo a quello calcolato analiticamente con le coordinate
cartesiane dei punti.
18
CALCOLO ANGOLO DI DIREZIONE(AB) – DIREZIONE ALLA BUSSOLA
Ö
Per calcolare l’angolo di direzione (AB) ci serviremo nuovamente delle coordinate
cartesiane dei due punti trigonometrici, che inseriremo nella formula
α = arctg
(X
(Y
B
B
- XA )
- YA )
L’angolo ottenuto è espresso nel sistema centesimale. In base al segno del numeratore e
del denominatore si procederà in un dei seguenti modi:
o
o
o
o
+
⇒ (AB) = angolo
+
+
⇒ (AB) = 200g - angolo
⇒ (AB) = 200g + angolo
⇒ (AB) = 400g – angolo
+
Nel nostro caso avremo:
α = arctg
(313.112,5 - 309.562,5 )
(4.620.287, 5 - 4.624.737, 5 )
=
-42g,8680
+
e quindi dovrò fare
200g - -42g,8680 = 157g,1320 angolo (AB) espresso in forma centesimale
141°,4188 angolo (AB) espresso in forma sessadecimale
141° 25’ 7,68” angolo (AB) in forma sessagesimale
Siamo nel caso
Ora l’angolo va corretto con la declinazione magnetica e la convergenza, valori che sono
riportati nella tabella, e che vanno calcolati ed aggiornati alla data odierna.
19
Come si può leggere dai dati sopra riportati, la declinazione magnetica al 1° gennaio
2000 valeva + 1° 20’ 00”, ed è stato calcolato che varia annualmente di + 0° 05’ 00”. È
presente inoltre una convergenza pari a - 1° 30’ 00”.
Bisogna ora calcolare quanto è variata dal 1° gennaio 2000 ad oggi.
Variazione della declinazione magnetica dal 1° gennaio 2000 al 1° gennaio 2006
Tempo trascorso: 6 anni
Variazione annuale: 0° 05’ 00”
0° 05’ 00” x 6 = 0° 30’ 00”
Variazione della declinazione magnetica dal 1° gennaio 2006 al 1°novembre 2006
Tempo trascorso: 10 mesi
Variazione mensile: (0° 05’ 00” / 12) = 0° 00’ 25”
0° 00’ 25” x 10 = 0° 04’ 10”
Variazione della declinazione magnetica dal 1° novembre 2006 al 22 novembre 2006
Tempo trascorso: 22 giorni
Variazione giornaliera: (0° 05’ 00” / 365) = 0° 0’ 0,82”
0° 0’ 0,82” x 22 = 0° 00’ 18,08”
Variazione totale della declinazione magnetica dal 1° gennaio 2000 al 22 novembre 2006
0° 30’ 00” + 0° 04’ 10” + 0° 00’ 18,08” = + 0° 34’ 28,08”
Declinazione magnetica aggiornata al 22 novembre 2006
(+ 1° 20’ 00”) + (+ 0° 34’ 28,08”) = 1° 54’ 28,08”
Correzione angolo di direzione – Direzione alla bussola
Angolo di direzione (AB) + Declinazione magnetica aggiornata + Convergenza
141° 25’ 7,68” + 1° 54’ 28,08” + (- 1° 30’ 00”) = 144° 49’ 35,7”
La direzione alla bussola da seguire per andare dal punto A al punto B sarà di
144° 49’ 35,7” S. E.
20
CALCOLO DEL DISLIVELLO TRA I DUE PUNTI TRIGONOMETRICI
Ö
Dalla carta di può leggere che:
o
o
Il punto trigonometrico Monte Cavo si trova alla quota di 949 m s.l.m.
Il punto trigonometrico Maschio dell’Artemisio si trova alla quota di 812 m s.l.m.
Le quote sopra riportate fanno riferimento al mareografo di Genova (1942).
Il dislivello tra due punti sarà dato dalla differenza delle due quote:
Dislivello AB = 949m s.l.m. – 812 m s.l.m. = 137 m
21
RILIEVO TOPOGRAFICO DI UNA STANZA
Planimetria della stanza in
scala 1:50
22
È stato effettuato il rilievo di una stanza. Dei lati e delle diagonali sono state effettuate
quattro misurazioni, con l’uso di tre diversi strumenti:
o
Fettuccia
o
Metro di legno
o
Metro da sarto
Una volta rilevate le diverse misure, ne è stata fatta la media matematica per avere il
valore più probabile della reale misura presa.
Sulla base della “Teoria degli errori”, è stato poi successivamente calcolato lo scarto
quadratico medio per ogni misurazione rilevata, usando la seguente formula:
∑ Vi 2
m=±
n -1
2
dove il termine ∑ Vi sta ad indicare le differenze tra la media matematica ed i singoli
valori ottenuti dalle quattro misurazioni poi elevate al quadrato e sommate tra loro;
dove il termine n – 1 sta ad indicare il numero di misurazioni fatte meno uno.
Di seguito viene riportata una tabella riassuntiva dei valori rilevati e calcolati durante il
rilievo della stanza.
FETTUCCIA
1°
MISURA
LATO
(cm)
L1
360,4
L2
350,6
L3
361,7
L4
361,9
d1
506,3
d2
510,2
METRO
METRO DA
DI
SARTO
LEGNO
2°
3°
4°
MEDIA
∑ Vi 2
MISURA MISURA MISURA MATEMATICA
(cm)
m=±
n -1
(cm)
(cm)
(cm)
(cm)
360,2
360
360,8
360,35
0,341565026
349,1
348,9
351,4
350
1,20277457
361,6
362
361,5
361,7
0,21602469
361,7
362,2
361,5
361,825
0,298607881
506,5
506,6
505,9
506,325
0,309569594
510,3
509,8
509,9
510,05
0,238047614
Una volta rilevate le misure e calcolati gli scarti quadratici medi, si è proceduto alla
rappresentazione in scala della stanza, usando il metodo dell’intersezione in avanti.
23
Come prima cosa è stato disegnato il lato L1, definita come base del disegno.
Sono stati poi tracciati gli archi puntando il compasso una volta nel vertice sinistro di L1
con apertura pari a d2, ed una volta puntando il compasso nel vertice destro di L1 con
apertura L4. Il punto di incrocio tra i due archi segna esattamente dove finisce il lato L4
che è poi stato rappresentato.
Costruzione grafica
scala 1:50
24
Lo stesso procedimento è stato seguito per rappresentare il lato L3, puntando prima il
compasso nel vertice destro di L1 con apertura pari a d2, e poi puntando il compasso nel
vertice sinistro di L1 con apertura pari a L3. Il punto di incrocio tra i due archi segna
esattamente dove finisce il lato L3 che è poi stato rappresentato.
Costruzione grafica
scala 1:50
25
Chiudendo poi il disegno, ecco che è stato ottenuto L2, come riportato nella planimetria
sottostante.
Planimetria schematica della stanza scala 1:50
LATO
L1
L2
L3
L4
d1
d2
MISURA (cm)
360,35 ±0,341565026
350 ±1,20277457
361,7 ±0,21602469
361,825 ±0,298607881
506,325 ±0,309569594
510,05 ±0,238047614
26
27
FOTOGRAMMETRIA
Con l’avvento della fotogrammetria l’uomo è riuscito ad effettuare rilievi del territorio
con l’ausilio di apposite apparecchiature fotografiche, aumentando così il livello della
precisione del rilievo, traendo vantaggi sia a livello qualitativo che a livello economico.
Le operazioni della fotogrammetria consistono nello scattare una serie di fotogrammi
dell’oggetto, determinando poi con una serie di lunghi e complessi calcoli matematici le
coordinate plano-altimetriche di ogni singolo punto, dopo ovviamente aver controllato sul
posto le zone che magari sono risultate scarsamente visibili, come ad esempio
avvallamenti particolarmente profondi.
La precisione della fotogrammetria è data dal fatto che con una fotografia del territorio
dall’alto si riescono a riportare fedelmente tutti i particolari e gli oggetti presenti nella
zona, senza preoccuparsi di dimenticarsene qualcuno. Così facendo, il fotogramma
sostituisce il libretto di campagna, sul quale l’operatore, durante il rilievo diretto sul
territorio doveva riportare in una scala opportuna tutti gli oggetti che venivano notati ad
occhio nudo nelle giuste loro posizioni.
Esistono diversi tipi di fotogrammetria:
Ö
Ö
Ö
Ö
fotogrammetria aerea: usata a scopi cartografici, per realizzare cartografie di
ampie zone con grande precisione
fotogrammetria terrestre: usata per scopi cartografici, realizzata da terra
esclusivamente in zone non facilmente visibili dall’alto (scarpate rocciose, valli
profonde, ecc…)
fotogrammetria speciale: usata per piccole misurazioni, come ad esempio in
campo medico per la visione di organi umani, o in campo industriale per
misurazione e creazione di carrozzerie, documentazioni di incidenti stradali
fotogrammetria architettonica: usata per il rilevo architettonico di particolari
strutturali di edifici, volte, prospetti piani ecc…
La prima fotogrammetria fu senza dubbio analitica. Bisognava infatti calcolare le
coordinate plano-altimetriche di ogni punto analiticamente, partendo dal fotogramma.
Verso i primi del ‘900 queste operazioni venivano effettuate con l’ausilio di mono o stereo
comparatori di immagine, con i quali le operazioni risultavano senza dubbio più semplici.
Evoluzione della restituzione analitica fu quella analogica, basata sul concetto si
proiezione ottica del fotogramma sia di tipo meccanica che ottico-meccanica.
Successivamente vennero affrontati diversi studi riguardo alla restituzione analitica, ma
i risultati ottenuti, anche se molto considerevoli, non potevano essere presi in
considerazione a causa della scarsa competitività dei prezzi delle apparecchiature
analitiche con quelle analogiche. Solamente in tempi recenti questa competitività
economica si è venuta a creare.
Verso il 1981 è stata proposta la possibilità di usare immagini digitali fotogrammetriche
dalle quali ricavare con estrema semplicità e velocità, grazie a calcolatori automatici, le
coordinate di ogni singolo punto in maniera del tutto automatizzata. Fu questo l’inizio
della restituzione digitale.
28
PROCESSO DEL RILIEVO FOTOGRAMMETRICO
Il rilievo fotogrammetrico consiste nel rilevare dai fotogrammi le coordinate X, Y e Z di
ogni singolo punto del fotogramma, usando solo le coordinate x e y dello stesso, con
operazioni matematiche.
Ciò può avvenire sia con l’uso di un solo fotogramma, (ottenendo con il suo
raddrizzamento un fotopiano), oppure con due fotogrammi di una stessa zona scattati da
angolazioni diverse che vengono poi disposti in maniera tale da permettere una
restituzione dell’immagine in tre dimensioni grazie alla fusione dei due fotogrammi
tramite una stereoscopio. In questo caso i fotogrammi vengono disposti nell’esatta
posizione in cui sono stati scattati, posti uno accanto all’altro e poi osservati
contemporaneamente ma separatamente.
I restitutori di immagini possono essere di tre tipi:
Ö
Ö
Ö
analogici: due portalastre nei quali vengono inseriti i fotogrammi orientati
esattamente come al momento dello scatto. Il tracciamento è eseguito da pantografi
collegati meccanicamente con le lastre
analitici: due portalastre che vengono mossi meccanicamente con impulsi
provenienti da un elaboratore, che le trasla automaticamente e simultaneamente. Il
tracciamento avviene con l’utilizzo di plotter che ricevono l’impulso direttamente dai
calcolatiri che estrapolano direttamente dai fotogrammi le coordinate ed effettuano
sul momento i calcoli
digitali: utilizza immagini a video, dette raster che, visionate con particolari
occhiali vengono visualizzate in tre dimensioni.
Il processo fotogrammetrico segue le seguenti fasi:
Ö
Ö
Ö
Ö
Ö
Ö
progetto di presa
presa dei fotogrammi
topografia d’appoggio
formazione dei modelli e delle triangolazioni aeree
restituzione grafica
ricognizione finale sul terreno e disegno da plotter o archiviazione
La presa dei fotogrammi viene effettuata con speciali camere metriche e realizzata in
modo che due fotogrammi consecutivi di sovrappongano almeno del 60% l’uno con l’altro.
Si ha così, con il giusto posizionamento, l’immagine tridimensionale attraverso lo
stereoscopio.
29
LE CAMERE DA PRESA
Le camere da presa vengono classificate in base all’angolo di campo di cui sono dotate,
cioè in base all’abbracciamento di territorio che riescono ad incorporare in un singolo
fotogramma.
Possono essere:
Ö
Ö
Ö
camere normali (per grandi scale)
camere grandangolari (per medie scale)
camere supergrandangolari (per piccole scale)
I fotogrammi sono in genere di dimensioni standard 23cm x 23 cm.
In base al campo di visione si determinano le seguenti focali di campo:
Ö
Ö
Ö
campo normale: 305 mm , 610 mm , 210 mm
campo grandangolare: 152 mm
campo supergrandangolare: 85 mm , 88 mm
Le camere da presa aeree sono molto ingombranti e pesano all’incirca 100 kg.
Sono dotate di molte apparecchiature ausiliarie, come quelle per la regolazione del tempo
di scatto tra un fotogramma e l’altro, della regolazione dell’inclinazione della macchina
da presa rispetto a quella dell’aereo, del caricamento della carta fotografica a rullo o
digitale.
Su una lastra sono presenti alcuni dati relativi allo scatto, come il numero progressivo
della tavola, la scala di rappresentazione, le coordinate di latitudine e longitudine, ora
data e luogo, griglia per le coordinate di ogni singolo fotogramma.
L’obbiettivo della macchina da presa viene costruito con una precisione molto alta, per
avere un immagine più vicina possibile alla realtà. Ogni macchina è accompagnata da un
certificato della casa costruttrice sul quale vengono riportate le caratteristiche tecniche
della stessa, come, dato molto importante, la distanza focale (f) ovvero la distanza del
centro dell’obbiettivo con la lastra.
L’otturatore viene costruito assieme al diaframma. Il tempo di apertura dell’otturatore
deve essere molto breve, per evitare l’effetto di trascinamento nei fotogrammi dovuto alla
velocità di movimento dell’aereo.
Macchina da presa aerea
30
GEOMETRIA DELLA PRESA
Con semplici relazioni matematiche si possono calcolare alcuni elementi geometrici utili
per il rilievo aerofotogrammetrico.
Si può ad esempio calcolare la quota di volo in base alla distanza focale (f) ed al rapporto
di scala media di rappresentazione del fotogramma (l su L, dove l sta per la grandezza
del fotogramma ed L la sua proiezione sul terreno in scala. Il loro rapporto è proprio la
scala media di rappresentazione grafica). Si parla di scala media perché non si può
garantire che tutti i punti sono alla stessa distanza H dalla machina da presa a causa
delle variazioni di quota del terreno. Si assume così un valore medio di H. Sappiamo che
la distanza focale (f), la quota di volo (H), la dimensione del lato del fotogramma (l) e la
sua proiezione sul terreno (L) sono legate dalla seguente relazione:
f:H = l:L
Da qui ne ricaviamo la quota di volo H.
Un altro fattore importante è il potere risolutivo dell’obbiettivo, perché con ciò si può
determinare la dimensione del più piccolo oggetto rappresentabile sul fotogramma in
maniera chiara e nitida.
La base di presa (b) nasce da una buona relazione tra il voler ottenere una buona
immagine stereoscopica e precisa. È stato calcolato che per avere queste precisioni
bisogna sovrapporre due fotogrammi consecutivi per almeno il 60%. La base di presa
sarà allora il restante 40% della lunghezza L.
Altro fattore da tenere conto è la sovrapposizione trasversale delle strisciate contigue.
Questa sovrapposizione deve essere tra il 10% ed il 20%, ciò per garantire che non
rimangano zone non rappresentate tra una strisciata e l’altra.
Per effettuare le strisciate l’aereo può seguire rotte nord-sud oppure est ovest. Perché si
possa effettuare correttamente u rilievo aerofotogrammetrico bisogna tener conto anche
di alcune condizioni meteorologiche:
assenza di nebbia o nuvole a bassa quota
assenza di forti raffiche di vento per evitare eccessivi spostamenti della rotta
dell’aereo
Ö raggi solari inclinati di un angolo superiore a 30°
- condizioni vegetative a terra ottimali per non coprire alcuni particolari
Ö
Ö
Con queste condizioni, le giornate utili per i rilievi aerofotogrammetrici sono davvero
poche.
31
Fotogrammetria Digitale
Oggi è molto diffuso l’utilizzo di immagini digitali create con apposite macchine digitali o
con la digitalizzazione di un fotogramma tramite scanner. Con il loro uso si è in grado di
rendere automatici molti processi fotogrammetrici, come l’orientamento dei fotogrammi,
il disegno delle relative cartografie per coordinate e la costruzione di modelli 3D,
lavorando anche con immagini di scarsa qualità.
Il processo di restituzione digitale di un’immagine precede i seguenti passaggi:
Ö
Ö
Ö
Ö
Ö
acquisizione dei fotogrammi tramite scanner
orientamento interno
creazione del modello 3D
elaborazioni automatizzate dell’immagine
elaborazioni di disegno manuale a video
E’ stata nominata nelle pagine precedenti l’immagine digitale, meglio nominata raster.
Questa immagine nasce dalla suddivisione dell’immagine fotografica in elementi di
dimensioni finite chiamati pixel, trasformando l’immagine in una matrice righe per
colonne. L’origine di questo sistema viene fissato per convenzione nell’angolo in alto a
destra del fotogramma.
È così possibile associare ad ogni singolo pixel delle coordinate. Per calcolare le
coordinate di un oggetto rappresentato nell’immagine basterà così calcolare la posizione
del pixel all’interno della matrice, calcolo che avviene in maniera del tutto automatica.
RISOLUZIONE DELL’IMMAGINE
La risoluzione di un’immagine è la nitidezza di rappresentazione della stessa, la
possibilità di individuare chiaramente il più piccolo oggetto presente.
Le risoluzione delle immagine possono essere di due tipi.
Parliamo di risoluzione radiometrica quando ci basiamo sulle gradazioni di colorazione
dell’immagine. In un’immagine ci sono 256 livelli cromatici differenti. Se l’immagine è in
bianco e nero, verrà fissato il valore 0 al colore nero, mentre il livello 255 al colore bianco.
L’intervallo tra i valori rappresenta ogni tipo di gradazione di grigio.
Se l’immagine è a colori, si divide ogni singola tonalità cromatica nei tre colori base rosso
giallo e verde, ai quali si affidano valori da 0 (assenza di colore) a 255 (saturazione del
colore).
La radiometria di un pixel a colori nasce dalla somma dei valori di ogni singolo colore
base.
Parliamo di risoluzione geometrica quando ci si riferisce direttamente alle dimensioni dei
pixel. È strettamente legata alla capacità di risoluzione delle macchine da presa e degli
scanner.
32
VISIONE STEREOSCOPICA NEL CAMPO DIGITALE
I sistemi di visione stereoscopica nel campo digitale sono sostanzialmente di sue tipi:
Ö
Ö
occhiali a polarizzazione attiva
schermo a polarizzazione attiva ed occhiali passivi
Ambedue i sistemi permettono la creazione di un’immagine tridimensionale dalla fusione
di due fotogrammi, che si viene a creare con la proiezione alternata dei due fotogrammi
ad alta frequenza, facendo visualizzare con l’occhio destro l’immagine destra e con
l’occhio sinistro l’immagine sinistra.
Nel primo caso si usano degli occhiali a polarizzazione, che, collegati al monitor, oscura
con le stesse frequenze di visualizzazione dell’immagine la vista dell’occhio destro e
sinistro.
Nel secondo caso è uno schermo a cristalli liquidi posto davanti al monitor ad oscurare
alternativamente le immagini. L’operatore indossa dei normali occhiali polarizzati che
permettono di visualizzare l’immagine in 3D.
ALGORITMI DI UN’IMMAGINE DIGITALE
Tramite questi algoritmi di autocorrelazione è possibile individuare automaticamente
immagini omologhe in due fotogrammi, i modo da poterli orientare correttamente con
una precisione pari alle dimensioni di un pixel.
Queste operazioni possono essere eseguite basandosi o in base ai valori radiometrici
dell’immagine o i base alle relazioni tra gli spazi geometrici presenti.
In generale si basano sulla comparazione delle gradazioni di grigio tra i pixel delle
immagini. Ci si aiuta con una matrice sagoma che viene tenuta ferma sull’oggetto da
cercare all’interno dell’altro fotogramma, e di una matrice di ricerca, che cerca
muovendosi all’interno del secondo fotogramma l’immagine analoga evidenziata nel
primo fotogramma dalla matrice sagoma.
Esistono due tecniche:
Ö
Ö
tecnica Cross-corelation che si basa sulla correlazione tra i livelli di grigio e che
fornisce una precisione al livello del pixel;
tecnica Least Squares Matching che considera anche le distorsioni
radiometriche e le deformazioni di immagine, ottenendo così una precisione
inferiore al pixel
Il processo di autocorrelazione avviene seguendo quattro punti:
Ö
Ö
Ö
Ö
selezione dell’entità per la correlazione dell’immagine
individuazione della corrispondente entità su un’altra immagine
calcolo della posizione nello spazio del punto considerato
valutazione della qualità della correlazione
Il primo punto sta a significare la ricerca automatica di punti facilmente individuabili
nel primo fotogramma
33
Il secondo riguarda la ricerca degli stessi all’interno di una seconda immagine,secondo i
metodi della scomposizione piramidale (si scompone l’immagine in immagini con
risoluzioni via via più base e si parte a cercare da quella con risoluzione più bassa) e
della geometria epipolare (basata sul presupposto che i fotogrammi sono fissati su un
unico piano e che quindi i unti possono essere cercati su di una stessa linea).
34
ESERCITAZIONE DI
AEROFOTOGRAMMETRIA
Piano di volo per rilievo aerofotogrammetrico
della regione Lazio
Ö
DATI DI PROGETTO
Scala 1 : 30.000
Distanza focale (f): 150 mm
Dimensioni fotogramma (l): 23 cm x 23 cm
Velocità Aereo: 200 km/h
Ö
CALCOLO DEL LATO DEL FOTOGRAMMA IN SCALA 1:30.000 PROIETTATO
SUL TERRENO (L)
Nota la scala di progetto, nota la dimensione dei lati del fotogramma, possiamo
impostare la seguente proporzione:
1 cm : 30.000 cm = 23 cm : X
X = 690.000 cm 6.900 m
Ö
CALCOLO DELLA QUOTA DI VOLO DELL’AEREO (H)
Sappiamo che la distanza focale (f), la quota di volo (H), la dimensione del lato del
fotogramma (l) e la sua proiezione sul terreno (L) sono legate dalla seguente relazione:
f:H = l:L
dove:
f = 150 mm 0,15 m
l = 23 cm 0,23 m
L = 6.900 m
Conoscendo I valori, impostiamo la proporzione:
0,15 m : H = 0,23 m : 6.900 m
H = 4.500 m
35
Ö
CALCOLO DELL’AREA DI UN FOTOGRAMMA PROIETTATA SUL TERRENO IN
SCALA 1 : 30.000
Sono note le dimensioni dei lati della porzione di terreno rappresentata all’interno di un
fotogramma. Pertanto possiamo calcolarne l’area:
A = L x L 6.900 m x 6.900 m = 47.610.000 m2 47,61 km2
Ö
CALCOLO DELLA BASE DI PRESA (b)
La base di presa b è definita come la distanza tra i centri di due fotogrammi, ed ha
valore pari al 40% di L, ovvero
40% di 6.900 m = 2.760 m 2,76 km
Ö
CALCOLO DEL TEMPO DI SCATTO TRA UN FOTOGRAMMA E L’ALTRO
Sapendo che l’aereo vola a 200 km/h (velocità minima perché l’aereo riesca a rimanere
sospeso in aria) e conoscendo la base di presa, possiamo impostare la seguente
proporzione, riportano le lunghezze in m e i tempi in secondi:
3.600 s : 200.000 m = X : 2.760 m
X = 49,68 s
Ö
CALCOLO DEL
SCATTARE
NUMERO
APPROSSIMATIVO
DI
FOTOGRAMMI
DA
Sappiamo che la superficie del Lazio misura 17.203 km2. Per regola, i fotogrammi
contigui presenti all’interno di una strisciata devono essere sovrapposti del 60% gli uni
agli altri (fotogramma 2 sovrappone il fotogramma 1 per il 60%, fotogramma 3
sovrappone il fotogramma 2 per il 60 % e così via…). Così facendo si ottiene un
fotogramma utile ogni tre fotogrammi continui sovrapposti. Proprio per questa ragione,
basta dividere la superficie del Lazio per il valore della superficie di un fotogramma
proiettato sul terreno e moltiplicare per tre il valore appena ottenuto, trovando così
approssimativamente il numero di fotogrammi da scattare per avere una visione
aerofotogrammetrica del Lazio.
17.203km 2
≈ 362 fotogrammi “puliti”
47,61km 2
362 x 3 = 1.086 fotogrammi sovrapposti
36