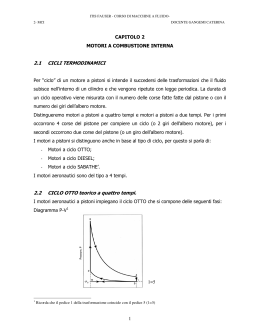
Termodinamica
Gas perfetto e sue leggi
1
Un po’ di chimica…
La materia è fatta di atomi distinti per
Massa molecolare:
somma delle masse atomiche di tutti gli
atomi che compongono la molecola.
Numero
atomico
Massa atomica
espressa in u
1
C12H22O11 molecola di zucchero
H
12 (12 u) +22 (u) + 11 (16u) = 342 u
1,0079
u è pari a 1/12 dell’isotopo C12
Ed è pari alla massa di un protone o
neutrone.
Mole (mol):
Quantità di materia che contiene NA =
6,02 * 1023 mol-1 particelle (numero di
Avogadro).
Corrisponde alla quantità di materia
tale che la misura in grammi della
sua massa sia pari alla massa
atomica o molecolare.
2
Applicazione
n (mol) 
massa (g)
massa molecolare (g/mol)
Consideriamo ora 12g di
Carbonio-12 calcoliamo la massa
in kg del singolo atomo di C
12 g / mol
 23
 26

1
,
99

10
g

1
,
99

10
kg
23
1
6,02 10 mol
Essendo u la dodicesima parte
della massa atomica del carbonio
1,99 1023g
1u 
 1,66 10 24 g  1,66 1027 kg
12
quindi
1kg  6,02 1026 u
3
Principio di Avogadro
Volumi uguali di
gas perfetti
Uno stesso numero
di molecole di gas
Alla stessa P
Alla stessa T
Alla stessa P
Alla stessa T
Contengono le stesse
molecole
Occupano lo stesso
volume
In particolare alla P = 1 atm e alla T = 0°C, 1 mole di gas occupa un
volume di 22,4 litri ( volume molare)
4
Sistema termodinamico
Un sistema termodinamico, S,
è costituito da tutti gli
elementi oggetto della nostra
osservazione.
L’ambiente esterno, A, è tutto
ciò che non appartiene al
sistema
L’ambiente universo è S U A,
l’unione del sistema e
dell’ambiente esterno.
5
Descrizione di un sistema
termodinamico
Sistema
termodinamico
Può essere
Aperto,
Chiuso,
Isolato
Per essere descritto
macroscopicamente
Temperatura T, Pressione p
Volume V, Densità d
Per misurarle
Eq. termico
Eq.
meccanico
Equilibrio termodinamico
Eq. chimico
6
Il gas perfetto:definizione e leggi
Una sostanza allo stato
aeriforme è detta
GAS PERFETTO
se soddisfa esattamente
le leggi di
Boyle Mariotte
Gay – Lussac
isobara
Gay - Lussac
isocora
7
Boyle Mariotte: isoterma (1660 circa)
La legge:
p V = costante
isoterme sul piano di Clapeyron
40,0
35,0
Pressione
30,0
25,0
20,0
Come realizzarla:
Immergendo il
sistema (cilindro con
pistone mobile) in
una miscela di
acqua e ghiaccio.
Variando il volume o
la pressione avremo
una isoterma a 0°C
(273 K)
15,0
10,0
5,0
0,0
Volume
8
Gay – Lussac: isobara (1800)
Come realizzarla:
La legge:
V = V0 (1+a t)
Dove V0 è il volume a temperatura 0°C.
Lasciando il pistone
libero di muoversi, la
pressione del gas intero
al cilindro sarà sempre
uguale alla pressione
atmosferica. La
temperatura e il volume
aumenteranno
linearmente
isobara sul piano di Clapeyron
1,2
1
pressione
0,8
0,6
0,4
0,2
0
0,0
0,2
0,4
0,6
0,8
1,0
1,2
1,4
1,6
1,8
2,0
volum e
9
Gay – Lussac: isocora (1800)
La legge:
P = P0 (1+a t)
Dove P0 è il volume a temperatura 0°C.
Isocora
2,0
1,8
1,6
1,4
Come realizzarla:
Bloccare il pistone oppure
zavorrare in modo
progressivo il pistone in
modo da mantenere il
volume costante. Ponendo
il sistema su una sorgente
di calore la temperatura e il
volume aumenteranno
linearmente.
pressione
1,2
1,0
0,8
0,6
0,4
0,2
0,0
0
0,5
volum e
1
1,5
10
Isocora in funzione della
temperatura
0,40
0,35
0,30
pressione (atm) o Pa
Poiché il valore a è indipendente dal
tipo di gas, è possibile realizzare un
termometro a gas utilizzando un
cilindro con pistone bloccato e con un
manometro registrare la variazione
della pressione.
0,25
0,20
0,15
0,10
0,05
-273,15 °C
0,00
0
50
100
150
temperatura ( °C)
200
250
11
Isobara in funzione della
temperatura
1,00
Se, mantenendo immutato l’intervallo di
temperature corrispondente ad 1 °C,
spostiamo lo zero a -273,15 °C,
otteniamo la
T (K) = t(°C) + 273,15
0,80
0,70
volume (cm^3)
SCALA TERMOMETRICA ASSOLUTA
o SCALA KELVIN K
0,90
0,60
0,50
0,40
0,30
0,20
-273,15 °C
0,10
0,00
0
50
100
150
200
250
temperatura (°C)
12
Leggi dell’isobara nella scala
K
La legge:
V = V0 (1+a t) Dove V0 è il volume a temperatura 0°C.
1


V  V0 1 
t  facendo il m.c.m.
 273,15 
 273,15  t 
V  V0 
 chiamando T  273,15  t e con T0  273,15
 273,15 
cioè passando alla scala termometr ica assoluta la legge si scrive :
VT
V 0
T0
similmente anche l' isocora verrà descritta dalla legge
p 0T
p
T0
13
La legge dei gas perfetti
Condizioni iniziali stato A
Temperatura T0 = 273 K = 0°C
Pressione = p0 e Volume = V0
Trasformazione isoterma A  B
V p
Vo' p  V0 p0 quindi Vo'  0 0
p
Trasformazione isobara B  C
p0
V
'
0
V
V p
V p
p
V  oT 
T  0 0 T  pV  0 0 T
T0
T0
pT0
T0
Ma per la legge di Avogadro fissati P0, T0 il volume V0 è proporzionale al numero
n di moli del gas
Equazione di stato pV  nRT dove R  8,3 J
mol  K
14