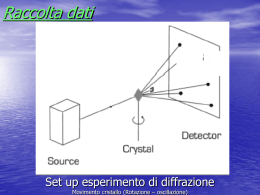
DIFFRAZIONE DI ONDE NEI CRISTALLI
Quando in cristallo si propaga un’onda con λ ≈ a,b,c si verifica diffrazione
dal suo studio è possibile ottenere informazioni su:
Simmetria del cristallo (tipo di reticolo)
Parametri reticolari
Struttura della cella elementare (posizioni atomi)
Diffrazione di raggi X (von Laue e Bragg, 1912-1913)
Diffrazione di elettroni (Davisson e Germer, 1927)
Diffrazione di neutroni (Shull, anni ‘50)
A secondo della natura dell’onda cambiano i centri di scattering
all’interno del cristallo:
Elettroni per diffrazione di raggi X
Elettroni e nuclei per diffrazione di fasci elettronici
Nuclei per diffrazione di fasci neutronici
Se consideriamo un fotone:
E fotone = hν =
hc
λ
= pc
λ ≈ A°
Raggi x
E ≈ 10 KeV
Se consideriamo particelle massive :
Diffrazione: interferenza fra onde diffuse elasticamente
G
k
G
r
G
k
G
ρ
O
G
r
P
Per raggi X i centri di scattering sono gli elettroni, mentre il contributo
dei nuclei è trascurabile
Se consideriamo una carica e di carica m accelerata da un campo
elettrico E:
eE
eE = ma ⇒ a =
m
D’altra parte l’elettrodinamica classica ci dice che la potenza media
irradiata dalla carica accelerata è (formula di Larmor o di Lienard):
2 e2 2
1
< P >=
a ∝ 2
3
3c
m
m M I ≈ 104 − 105 m
- Onda diffusa ha la stessa frequenza di quella incidente
- Ampiezza dell’onda diffusa dall’elettrone è data da:
Formula di Thomson
Scattering elastico
classico
Nel caso in cui l’onda incidente sia costituita da un fascio di neutroni:
l’interazione avviene quasi esclusivamente con i nuclei. In realtà
esiste una debole interazione fra i momenti magnetici di spin dei
neutroni e degli elettroni, che tuttavia è significativa solo per solidi
ferromagnetici o antiferromagnetici
Nel caso in cui l’onda incidente sia costituita da un fascio di elettroni:
L’interazione avviene sia con i nuclei che con gli elettroni del
cristallo e lo scattering è con il potenziale elettrostatico del cristallo
Ricordiamo che per onde materiali, l’intensità è il numero di partic.
che attraversano l’unità di superficie nell’unità di tempo.
G
k
S
D
G
ρ
O
Rρ
θ
φ
G
r
α
G
R
P
B
φ'
rρ
φ ≡ arcos(rˆ ⋅ kˆ)
φ ' ≡ arcos( Rˆ ⋅ kˆ)
θ ≡ arcos( ρˆ ⋅ Rˆ )
α ≡ arcos(rˆ ⋅ Rˆ )
G
G
α → 0 r ≈ // R
φ'≈φ
DBP triangolo “quasi” isoscele
(DP-BP) << r
r ≈ R − ρ cosθ
DP ≈ BP = OP - OB
F ampiezza in P
dell’onda diffusa
F = F0e
F = F0 A(φ )
e
G G
ik ⋅ρ ik ( R − ρ cos θ )
e
R − ρ cos θ
ρ cos θ
R
Definendo:
G
k ' ≡ kRˆ
eikr
A(φ )
r
G G
ik ⋅ρ − ik ρ cos θ
e e
= F0 A(φ )
R ⎛ ρ cos θ ⎞
⎜1 −
⎟
R
⎝
⎠
ˆ
eikR ikG⋅ρG −ik ρ ( ρˆ ⋅R )
F ≈ F0 A(φ )
e e
R
e
ikR
G G
ik ⋅ρ
F = F0 A(φ )
e
1
ikR
R
e
cos θ = ρˆ ⋅ Rˆ
G G
G G
ik ⋅ρ − ik '⋅ρ
e
F = F0 A(φ )
JJG G G
∆k ≡ k '− k
e
ikR
R
e
G G
G G
ik ⋅ρ − ik '⋅ρ
e
eikR −i∆kG⋅ρG
F = F0 A(φ )
e
R
G
G
k'
k
φ ≈ φ ' ≡ arcos( Rˆ ⋅ kˆ) = arcos(rˆ ⋅ kˆ ')
φ
JJG
∆k
Questa è l’ampiezza dell’onda diffusa in P da un unico centro
di scattering posto in ρ ≡ρ0 ma in un cristallo ho più centri di
scattering equivalenti per simmetria…
G
ρ = ρ0 + n1τ1 + n2τ 2 + n3τ 3 = ρ0 + n1tn
G
G
G
G
G
G
G
Ogni punto
ρ0
della cella elementare produce un contributo
G JJG
− i ρ 0 ⋅∆ k
e
questo contributo
G derivanti da altri punti
G va sommato a quelli
connessi a ρ 0 da una traslazione
τ
:
= e
n1
e
G JJG
− i t n ⋅∆ k
=1
G G G
∆k = G ≡ h
G JJG
− i ρ 0 ⋅∆ k
G JJG
⎡
− i t n ⋅∆ k ⎤
⎢∑ e
⎥
⎣ n
⎦
Legge di Laue della diffrazione reticolare
JJG G G
∆k = G ≡ h
I tot ∝
= I1I 2 I 3
I∝
1− qN
∑ q = 1− q
n =1
N
n
2⎛
x ⎞
sin ⎜ N ⎟
⎝2 ⎠
f ( x) ≡
2⎛ x⎞
sin ⎜ ⎟
⎝2⎠
con
G JJG
x ≡ τ ⋅ ∆k
altezza picchi principali ≈ N2
Area picchi principali ≈ N2 (4π/N) ≈ N
Posizione picchi principali= 0 +2πn
JJG G
∆k = G
Connessione fra legge di Laue e legge di Bragg
φ = 2θ
2d sin θ = nλ
2sin θ
λ
n
=
d
2π
2
sin θ =
n
λ
d
JJG 2π
G
2k sin θ =| ∆k |=
n =| G |
d
2π
2d sin θ = nλ
per
n ≠1
per
θ = 900 2d = nλ
λmax = 2d
n =1
λ sottomultiple di λmax e diffrazione di ordine n
Condizione di Laue
Condizione di Bragg
2d sin θ = nλ
JJG
G
G
2π
| ∆k |=| G |= n | G0 |=
n
d
Al crescere di G
crescere di n
λ ≤ 2d
2d sin θ
λ=
n
diminuire λ
λ≈d
dimiunisce I
Fattore di struttura
eikR −i∆kG⋅ρG0
F = F0 A(φ )
e
R
Contributo del
singolo centro
di scattering
N
Ftot = ∑
∑ Fn,i
n =1 i∈Ωc
cos t (φ , R)
G
eikR −i∆k ⋅ρGn ,i
eikR
e
= ∑ ∑ F0 A(φ )
= F0 A(φ )
R
R
n =1 i∈Ωc
N
N
∑∑e
G G
− i∆k ⋅ρ n ,i
n =1 i∈Ωc
P
G
k
G
ρ0
O
G
R
∫
G
n ( ρ 0 )e
G G
− i∆k ⋅ρ0
G
d ρ0
Ωcell
densità di centri di scattering
I tot
G G ⎞
G G
N
⎛
G
− i∆k ⋅ρ n
− i∆k ⋅ ρ0 G
2
d ρ0
=| Ftot | = C (φ , R) ⎜ ∑ e
⎟ ∫ n( ρ 0 )e
⎝ n=1
⎠ Ωcell
2
C (φ , R ) ≡| cos t (φ , R) |2
I tot =| Ftot | = C (φ , R )
2
∫
G
n ( ρ 0 )e
G G
− i∆k ⋅ρ0
2
G
N
∑e
d ρ0
n =1
Ωcell
= C (φ , R )
∫
Ωcell
G
n ( ρ 0 )e
G G
− i ∆k ⋅ ρ 0
G G 2
− i ∆k ⋅ ρ n
2
G
d ρ0 I1I 2 I 3
JJG
G
⎞
2 ⎛ τ 1 ⋅ ∆k
sin ⎜
N1 ⎟
2
⎝
⎠
I1 ≡
JJG
G
⎛
2 τ 1 ⋅ ∆k ⎞
sin ⎜
⎟
⎝ 2 ⎠
lim N1 →∞ I1 ≠ 0
G JJG
lim N1 →∞ I1 = 2π N1δ (τ1 ⋅ ∆k )
per
G JJG
τ1 ⋅ ∆k = 0 + 2π n
JJG G
∆k = G
JJG G
lim N1 →∞ I1 = 2π N1δ (∆k − G )
I tot = C (φ , R )
∫
G
n ( ρ 0 )e
G G
− i∆k ⋅ρ0
2
G
d ρ0 I1I 2 I 3
Ωcell
I tot = C (φ , R )
∫
G
n( ρ 0 )e
G G
− i∆k ⋅ρ0
2
G
d ρ0
G G
(2π ) N1 N 2 N3δ (∆k − G )
3
Ωcell
N
∫
I tot = C (φ , R )
G
n( ρ 0 )e
G G
− i ρ0 ⋅G
2
G
d ρ0
G G
(2π ) N δ (∆k − G )
3
Ωcell
∫
Ωcell
G
n ( ρ 0 )e
G G
− i ρ0 ⋅G
G
d ρ0 ≡ ζ (G )
G
Fattore di struttura
I tot
G G
G 2
= (2π ) N C (φ , R) ζ (G ) δ (∆k − G )
3
JJG G
La condizione di Laue, ∆k = G , rappresenta quindi solo una condizione
I tot ≠ 0
necessaria ma non sufficiente perché
G
ζ (G ) ≠ 0
G
n( ρ 0 ) =
Nbase
G
G
∑ n j ( ρ0 − ρ j )
j =1
occorre anche che:
G
ζ (G ) =
G
∫
n ( ρ 0 )e
G G
− i ρ0 ⋅G
d ρ0 ≈
Ωcell
=
Nbase
∑e
j =1
G
f j (G )
G
Nbase
∑ ∫
j =1
G
G
n j ( ρ0 − ρ j )e
G G
− i ρ0 ⋅G
G
d ρ0
Ωcell
G G
− i ρ j ⋅G
∫
G −i ρG ⋅GG G
n j ( ρ )e
dρ
G G
G
ρ ≡ ρ0 − ρ j
Ωcell
G
Fattore di forma atomico
G Nbase −i ρG j ⋅GG
G
ζ (G ) ≈ ∑ e
f j (G )
j =1
Fattore geometrico
G
ai struttura S (G )
G G
ρ0 = ρ + ρ j
G
G
d ρ0 = d ρ
Se atomi nella base sono uguali
G
G Nbase −i ρG j ⋅GG
G
G
ζ (G ) ≈ f (G ) ∑ e
≡ f (G ) S (G )
j =1
G
G −idG ⋅GG
G −idG ⋅GG
ζ (G ) = f A (G )e A + f B (G )e B
G
G
d A = −d B
In conclusione:
JJG G
∆k = G
JJG 2π
G
2k sin θ =| ∆k |=
n =| G |
d
Consentono di determinare il reticolo reciproco e la distanza fra
piani reticolari
G
ζ (G ) =
∫
G
n ( ρ 0 )e
G G
− i ρ0 ⋅G
d ρ0 ≈
Ωcell
Nbase
∑ ∫
j =1
G
G
n j ( ρ0 − ρ j )e
G G
− i ρ0 ⋅G
G
d ρ0
Ωcell
G Nbase −i ρG j ⋅GG
G
ζ (G ) ≈ ∑ e
f j (G )
j =1
G
Consentono di ottenere informazioni
sulla posizione e caratteristiche dei
centri di scattering all’interno di una
cella elementare
G
G Nbase −i ρG j ⋅GG
G
G
ζ (G ) ≈ f (G ) ∑ e
≡ f (G ) S (G )
j =1
Effetto termico di vibrazione e fattore di Debye-Waller
L’effetto delle vibrazioni atomiche all’interno di un cristallo è quello
di ridurre l’intensità diffratta di un fattore, detto fattore di Debye-Waller
che dipende in maniera esponenzialmente decrescente da T e G2
I DW = e
−
kBTG 2
3M ω 2
M = massa totale degli atomi all’interno della cella
ω = frequenza media di vibrazione degli atomi
G G
G
r (t ) = ρ + u ρ (t )
Oscillatori armonici indipendenti
per
Karm
G
∆k // zˆ
(
G JJG
u ⋅ ∆k
)
2
=
(
JJJJG
u z | ∆k |
)
2
JJJJG 2
JJJJG
JJJJG
2
2
| ∆k |
= u z2 | ∆k | = | ∆k | u z2 =
u2
3
k BT
< u >=
M ωm 2
2
2
1
⎛ − 1 <u 2 >|∆k |2 ⎞
− < u 2 >|∆k |2
⎟ =e 3
I = ⎜e 6
⎜
⎟
⎝
⎠
JJG
I ∆k = I0 IDW = I0
( )
kBTG2
−
2
M
3
ω
e
CONDIZIONI
PER LA
CONDIZIONI SPERIMENTALI
SPERIMENTALI PER
LA DIFFRAZIONE
DIFFRAZIONE
Solo se la superficie della sfera
contiene i vertici di vettori del
reticolo reciproco è possibile
la diffrazione
Costruzione di Ewald
E’ sempre possibile verificare la
condizione di Laue ruotando il
centro della sfera attorno ad O,
ossia ruotando il cristallo, oppure
variando λ
METODO DI LAUE
METODO DEL
CRISTALLO
ROTANTE
JJG
G
| G | = | ∆ k | = 2 k s in θ
G
| G |≤ 2 k
METODO DELLE POLVERI o dI DEBYE - SCHERRER