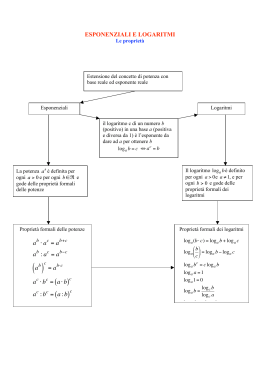
CAPITOLO 3: EQUILIBRI DI FORMAZIONE DI COMPLESSI.
1. Introduzione.
In un contesto analitico per complesso si intende una qualsiasi specie esistente in soluzione data
dalla combinazione di due o più specie semplici capaci di esistenza autonoma in soluzione. La loro
formazione è interpretabile, per lo più, sulla base della teoria di Lewis e cioè a seguito della
formazione di legami dativi tra donatori e accettori di doppietti di elettroni. Di norma in un
complesso si individua un nucleo (chiamato accettore) circondato da dei leganti per cui si definisce
numero di coordinazione il numero di leganti legati all'accettore. A seconda della natura e del
numero di accettori e di leganti il complesso può essere:
carico (positivamente o negativamente)
neutro
mononucleare (presenza di un solo accettore)
polinucleare (presenza di più accettori)
chelato (il legante lega, chela, l'accettore con più legami).
Il coinvolgimento di una specie in un complesso ne condiziona le proprietà ed in particolare la
solubilità, il potenziale redox, la disponibilità verso altre reazioni di equilibrio (effetto competitivo
tra reazioni). In particolare le reazioni di formazione di complessi possono essere utilizzate per fini
analitici quali e quantitativi. L'applicazione quantitativa prevede o l'impiego di opportuni metodi di
calibrazione o la procedura della titolazione. Per un impiego analitico le reazioni di formazione di
complessi devono essere quantitative, stechiometriche e rapide.
quantitative: formazione completa del complesso (costante di formazione molto elevata o eccesso di
legante).
stechiometriche: si forma un'unica specie di stechiometria ben definita e non più specie fra loro in
equilibrio.
rapide: l'equilibrio è raggiunto velocemente.
In generale i leganti monodentati danno reazioni veloci ma non utilizzabili a fini quantitativi a causa
dell'instaurarsi di stadi successivi di equilibrio con costanti usualmente simili mentre i leganti
chelanti in genere danno stechiometrie 1:1 con elevati valori della costante di equilibrio ma con
velocità di reazione talvolta bassa.
2.Complessi mononucleari
Data una coppia Mm+, generico metallo-ione accettore, ed Ll-, generico legante, gli equilibri che si
possono instaurare sono
M
m+
(m-l)+
+ L ↔ ML
(m-l)+
ML
l-
l-
+ L ↔ ML2
(m-2l)+
K1 =
ML( m− l) +
= β1
M m+ Ll −
K2 =
(III.2.1)
ML(2m − 2 l ) +
(III.2.2)
ML( m − l ) + Ll −
ML(2m − 2 l ) +
K1 ⋅ K 2 =
M
m+
l− 2
= β2
(III.2.3)
⋅ L
e quindi in generale
ML(km−−1kl+ l) +
l−
+L
⇔ML(km− kl) +
Kk =
ML(km − kl ) +
ML(km−−1 kl + l ) +
K1K 2 .... K k =
l−
L
ML(km − kl ) +
M
m+
(III.2.4)
l− k
=βk
(III.2.5)
⋅ L
dove con K si intendono le costanti di stadio e con β le costanti cumulative di formazione. Se si
opera in soluzione acquosa accanto agli equilibri sopra scritti sono operanti eventuali altri equilibri
del metallo e del legante condizionati principalmente dal pH della soluzione. Il metallo-ione, se di
carica elevata, può dare complessi con lo ione ossidrile e/o precipitare come idrossido mentre il
legante può sottostare ad equilibri di protonazione. Per un catione bicarico, M2+ ed un legante L- si
possono avere ad esempio gli equilibri competitivi:
2+
-
+
M + OH ↔ MOH
K OH =
MOH +
M 2 + OH −
(III.2.6)
2
K s = M 2 + OH −
M2+ + 2 OH- ↔ M(OH)2
-
+
Ka =
L + H3O ↔ HL + H2O
2
H 3O + L−
(III.2.7)
(III.2.8)
HL
L'analogia formale tra sistemi poliprotici e complessi, le particelle scambiate sono H+ ed Llrispettivamente, trova riscontro nella derivazione di relazioni del tutto equivalenti alle II.11.10II.11.13. Dalla combinazione dei bilanci di massa del metallo-ione e del legante
CM = [Mm+] + [ML(m-l)+] + [ML2(m-2l)+] + ....... + [MLn(m-nl)+]
(III.2.9)
CL = [Ll-] + [ML(m-l)+] + 2[ML2(m-2l)+] + .......
+ n[MLn(m-nl)+] + [HL(l-1)-]+...+ [HlL]
(III.2.10)
con le III.2.1-III.2.5 si ottengono le frazioni, αi, delle varie specie contenenti il metallo in perfetta
corrispondenza con quanto derivato per gli equilibri acido base. Si ha:
αM =
M m+
α ML =
CM
=
1
1 + β 1 Ll − + β 2 Ll −
ML( m−l) +
CM
2
+ ...... + β n Ll −
n
≡ α0
β1 Ll −
=
l−
1 + β1 L
l− 2
+ β2 L
(III.2.11)
≡ α1
l− n
+ ...... + β n L
(III.2.12)
.........................................................................................
α MLn =
ML(nm− l) +
CM
=
β n Ll −
1 + β 1 Ll − + β 2 Ll −
2
n
+ ...... + β n Ll −
n
≡ αn
(III.2.13)
E' da notare la indipendenza degli αi dalla concentrazione dell'accettore, quando si abbia la
formazione di soli complessi mononucleari. L'analogia tra equilibri acido-base e di formazione di
complessi si sviluppa ovviamente anche negli approcci metodologici della loro trattazione, in
particolare anche nell'uso dei diagrammi logaritmici in cui l'ordinata rappresenta il logaritmo delle
concentrazioni di equilibrio e l'ascissa il pL, cioè ancora il logaritmo negativo della particella
scambiata.
Per il sistema Cu2+, accettore, e trietilentetraammina (NH2-CH2CH2NH-CH2CH2NH-CH2CH2NH2,
Trien), legante, come per un acido debole monoprotico, si ha:
3
2+
2+
K=
Cu + Trien ↔ [Cu(trien) ]
Cu ( Trien ) 2 +
Cu 2 + Trien
(III.2.14)
CCu = [Cu2+] + [Cu(Trien)2+]
(III.2.15)
CTrien = [Trien] + [Cu(Trien)2+]
(III.2.16)
Se CCu è la concentrazione analitica di Cu2+ e se si trascura l'insorgenza di qualsiasi equilibrio acido
base si può scrivere:
Cu 2 + = C Cu α
Cu2 +
1
1 + K Trien
= C Cu
[Cu (Trien) ] = C (1 − α ) = C
2+
Cu 2 +
Cu
Cu
K [Trien]
1 + K [Trien]
(III.2.17)
(III.2.18)
Si individuano tre situazioni:
K [Trien] << 1, K [Trien] ≈ 1, K [Trien] >> 1
Per K [Trien] << 1
Cu 2+ = C Cu
,
log Cu 2+ = log C Cu
(III.2.19)
Cu ( Trien ) 2+ = C Cu K Trien
log Cu ( Trien ) 2+ = log C Cu K + log Trien
(III.2.20)
Nel DL di fig.III.1 le III.2.19 e III.2.20 sono due rette di cui la prima di pendenza nulla e la seconda
di pendenza -1.
Per K [Trien] = 1
Cu 2 + = Cu ( Trien ) 2 + =
C Cu
2
log Cu 2 + = log Cu ( Trien ) 2 + = log C Cu − log 2
(III.2.21)
Avendo le due specie concentrazioni uguali i corrispondenti valori si collocano nel DL a 0.3 unità
logaritmiche al di sotto di CCu.
4
Per K [Trien] >> 1
Cu 2+ =
C Cu
C
; log Cu 2+ = log Cu − log Trien
K Trien
K
(III.2.22)
Cu ( Trien ) 2+ = C Cu ; Cu ( Trien ) 2+ = log C Cu
(III.2.23)
Il raccordo dei tratti rettilinei con quelli curvi viene fatto, come visto per le reazioni acido-base, a
±1.3 unità logaritmiche dal punto sistema che è individuato dalle coordinate -log K, log CCu. Per
quanto riguarda [Trien] essa è rappresentata da una retta di pendenza -1 in quanto
pTrien = -log [Trien]
(III.2.24)
pTrien
0
0
5
10
15
20
25
30
[Cu2+]
[Cu(Trien)2+]
-5
-15
-20
n]
rie
[T
log [Ci]
-10
-25
-30
Fig.III.1. DL del sistema Cu2+/Trien. CCu = 10-2 M, log K = 20.4.
5
(EDA =
Un secondo esempio, analogo ad un sistema biprotico, è dato dal complesso Cu ( EDA ) 2+
n
NH2CH2CH2NH2, etilendiammina, legante bidentato) con n = 1, 2. Si ha
Cu
2+
2+
K1 =
+ EDA ↔ Cu(EDA)
2+
Cu(EDA) + EDA ↔ Cu(EDA)2
2+
K2 =
Cu ( EDA ) 2 +
= β1
Cu 2+ EDA
(III.2.25)
Cu ( EDA ) 22 +
(III.2.26)
Cu ( EDA ) 2 + EDA
K1 ⋅ K 2 =
Cu ( EDA ) 22 +
Cu 2 + EDA
2
= β2
(III.2.27)
CCu = [Cu2+] + [Cu(EDA)2+] + [Cu(EDA)22+]
(III.2.28)
CEDA = [EDA] +[Cu(EDA)2+] +2[Cu(EDA)22+]
(III.2.29)
Trascurando ancora equilibri competitivi acido-base il DL del sistema Cu2+/EDA, riportato in
fig.III.2 per CCu=10-2 M, si ottiene diagrammando log[EDA], log[Cu(EDA)2+] e log[Cu(EDA)22+]
vs. pEDA. Si può scrivere:
Cu 2 + = C Cu α
Cu2 +
= C Cu
Cu ( EDA ) 2 + = C Cu α
Cu ( EDA ) 22 + = C Cu α
1
1 + β1 EDA + β 2 EDA
Cu( EDA ) 2 +
Cu( EDA ) 2 +
2
= C Cu
= C Cu
(III.2.30)
2
β1 EDA
1 + β 1 EDA + β 2 EDA
β 2 EDA
2
(III.2.31)
2
(III.2.32)
2
1 + β 1 EDA + β 2 EDA
che nelle varie zone sono riconducibili a relazioni più semplici, lineari. Si noti che la differenza tra
le costanti di stadio, inferiore a 2.6 unità logaritmiche, fà sì che il complesso 1:1 non raggiunga mai
la concentrazione analitica,10-2 M.
6
pEDA
0
0
3
6
9
12
15
[Cu2+]
[Cu(EDA)22+]
-9
[C
u(
ED
A
) 2+
]
-6
A
D
[E
log [Ci]
-3
]
-12
-15
Fig.III.2. DL del sistema Cu2+/EDA. CCu = 10-2 M, log K1 = 10.7, log K2 = 8.9.
L'assenza di un intervallo di concentrazione di legante in cui il complesso intermedio presenta un
valore di α unitario è ancora più evidente nel caso dei complessi ammoniacali dello ione Ag+ per i
quali il valore di K1 è addirittura minore di quello di K2.
[Ag (NH ) ] = K
+
+
+
3
[Ag ][NH ]
Ag + NH3 = Ag(NH3)
+
(III.2.33)
1
3
+
Ag(NH3) + NH3 = Ag(NH3)2
+
[Ag (NH ) ] = K
[Ag (NH ) ][NH ]
+
3 2
+
3
2
(III.2.34)
3
Nel tracciare il DL riportato in fig.III.3 sono nuovamente ignorati gli equilibri acido-base ed i punti
sistema contrassegnati con le lettere a e b sono dati ancora dai valori di log K1 e log K2.
7
pNH3
0
0
1
2
3
4
5
6
-1
[Ag+]
c
a
b
]
H3
[N
-4
3
H
) +]
-3
[A
g(
N
log [Ci]
-2
[Ag(NH3)2+]
-5
-6
Fig.III.3. DL del sistema Ag+/NH3. CAg = 10-2 M, log K1 = 3.32, log K2 = 3.89.
Dall'esame del grafico si ottengono immediatamente le seguenti informazioni:
nel punto a si ha:
[Ag+] = [Ag(NH3)+]
(III.2.35)
da cui
NH 3 = K1−1
(III.2.36)
Nel punto b
[Ag(NH3)+] = [Ag(NH3)2+]
(III.2.37)
8
da cui
NH 3 = K 2−1
(III.2.38)
Nel punto c
[Ag+] = [Ag(NH3)2+]
(III.2.39)
da cui
NH 3 =
K1−1 K 2−1
(III.2.40)
Anche nel caso dei complessi il diagramma logaritmico fornisce velocemente le risposte a vari
quesiti. Ad esempio il DL di fig. III.3 può dare il valore delle concentrazioni delle varie specie
all'equilibrio per il sistema CAg = 10-2 M e CNH3 = 10-1 M (si trascura l'interazione con H2O).
Essendo
][
]
= [NH ] +[Ag ( NH ) ]+ 2[Ag ( NH ) ]
[
][
C Ag = Ag + + Ag ( NH 3 ) + Ag ( NH 3 )2
C NH 3
+
+
+
3
3
+
3 2
(III.2.41)
(III.2.42)
moltiplicando la III.2.41 per 2, sottraendo membro a membro e riarrangiando si ottiene
2 Ag + + Ag ( NH 3 ) + + 8 ⋅ 10 −2 = NH 3
(III.2.43)
che è una condizione di ugualianza che deve valere all'equilibrio. Essa rappresenta un bilancio di
legante, analogo al bilancio protonico, relativo al sistema pensato come [NH3] 8·10-2 M, eccesso di
ammoniaca, [Ag(NH3)2+] =10-2 M. Con lo schematismo già utilizzato per gli acidi si può scrivere:
9
Ag +
+2
↑
Ag ( NH 3 )
+1
+
↑
0 − − − − − Ag ( NH 3 )2
+
↓
NH 3
−1
dove per livello 0 si sceglie il complesso con più alto numero di coordinazione a seguito della
presenza di un eccesso di legante. La concentrazione di ammoniaca deve essere comprensiva di
quella generata dalla dissociazione del complesso (livello -1) e dell'eccesso (8·10-2 M). Dal DL si
verifica la validità dell'approssimazione 8·10-2 = [NH3] essendo trascurabili il catione libero ed il
complesso 1:1. Tracciando una verticale passante per il punto di incrocio si determinano tutte le
concentrazioni all'equilibrio.
In modo del tutto analogo si possono calcolare le concentrazioni di equilibrio per il sistema CCu =
10-2 M e CNH3 = 10-2 M (si trascura l'interazione con H2O). Dalla combinazione dei due bilanci di
massa
][
][
][
]
= [NH ] +[Cu ( NH ) ]+ 2[Cu ( NH ) ] + 3[Cu ( NH ) ] + 4[Cu ( NH ) ]
[
][
C Cu = Cu 2+ + Cu ( NH 3 ) + Cu ( NH 3 )2 + Cu ( NH 3 )3 + Cu ( NH 3 )4
C NH 3
2+
2+
2+
3
3
2+
2+
3 2
2+
2+
3 3
2+
3 4
(III.2.44)
(III.2.45)
si ottiene
[Cu ] = [NH ] +[Cu(NH ) ]+ 2[Cu(NH ) ]+ 3[Cu(NH ) ]
2+
3
2+
3 2
2+
3 3
2+
3 4
(III.2.46)
Pensando il sistema come costituito da Cu(NH3)2+ = 10-2 M che si equilibra lo schema è
10
+1
Cu 2+
↑
0 − − − − − Cu (NH 3 )
2+
↓
− 1 NH 3 , Cu ( NH 3 )2
2+
↓
−2
Cu ( NH 3 )3
2+
↓
−3
Cu ( NH 3 )4
2+
da cui
[Cu2+] = [Cu(NH3)22+] + 2 [Cu(NH3)32+] + 3[Cu(NH3)42+] + [NH3]
che è proprio la III.2.46. Dal DL di fig.III.4 si evidenzia
[Cu2+] = [Cu(NH3)22+]
(III.2.47)
e per quella ascissa si possono leggere le concentrazioni di tutte le specie in soluzione.
11
pNH3
0
0
1
6
(N
u
[C
H
)3
3
[Cu2+]
]
3 ) 2+
2 ]
[Cu
(NH
3 ) 2+]
-5
5
[Cu
(N
H
log [Ci]
-4
4
[Cu(NH3)42+]
2+
-3
3
]
H3
[N
-1
-2
2
-6
-7
-8
Fig. III.4. DL del sistema Cu2+/NH3. CCu = 10-2 M, log K1 = 4.31, log K2 = 3.67, log K3
= 3.04, log K4 = 2.30. La verticale permette di leggere i valori delle concentrazioni
all'equilibrio nel caso di CCu = CNH3 = 10-2 M.
3. Equilibri competitivi, limiti del DL, costanti condizionali
I leganti molto spesso oltre che basi di Lewis sono anche basi di Brönsted per cui sottostanno anche
ad equilibri di tipo acido-base (NH3, CN-). La presenza di equilibri competitivi rende molto più
complessa la rigorosa descrizione del sistema impedendo, in linea di principio, la diretta
applicazione dei DL sopra descritti poichè accanto agli equilibri di formazione dei complessi
devono essere considerati anche quelli antagonisti acido-base. Prendendo in considerazione il
sistema argento amminico visto in precedenza si può verificare quanto accurata sia la descrizione
12
grafica sopra descritta e come il pH influenzi la formazione dei complessi. Le specie effettivamente
presenti in una soluzione di AgNO3 ed NH3 sono NH3, NH4+, Ag+, Ag(NH3)+, Ag(NH3)2+, H3O+,
OH- ed NO3- cui corrispondono le seguenti relazioni:
K w = H 3O + OH −
(III.3.1)
NH 3 H 3O +
Ka =
(III.3.2)
NH 4+
[Ag (NH ) ]
+
β1 =
3
[Ag ][NH ]
(III.3.3)
+
3
[Ag (NH ) ]
+
3 2
β2 =
(III.3.4)
[Ag ][NH ]
= [NH ] + [NH ] + [Ag ( NH ) ]+ 2[Ag ( NH ) ]
= [Ag ] + [Ag (NH ) ]+ [Ag ( NH ) ]
+
2
3
C NH 3
C Ag
3
+
+
4
+
3 2
3
+
+
(III.3.5)
+
3 2
3
(III.3.6)
C Ag = NO 3−
(III.3.7)
[H O ] + [NH ] + [Ag ]+ [Ag (NH ) ]+ [Ag (NH ) ] = [OH ] + [NO ]
+
3
+
4
+
+
+
3 2
3
−
−
3
(III.3.8)
Disponendo di 8 equazioni in 8 incognite il sistema è risolvibile fornendo i valori delle
concentrazioni delle specie in equilibrio. Per il caso CAg = CNH3 =10-2 M dalla combinazione delle
III.3.1-III.3.8 si giunge a
 Ka
 [NH 3 ] 
C
2
1 +

[
]
[
]
1
NH
NH
=
−
−
β
2
3
3 
K a 1 + β1 [NH 3 ] + β 2 [NH 3 ]2

 [NH 3 ]
(
)
(III.3.9)
=
Kw

 Ka
C
2
1 − β 2 [NH 3 ] − [NH 3 ]

2
1 + β1 [NH 3 ] + β 2 [NH 3 ]
 [NH 3 ]
(
)
la cui soluzione grafica è data in figura III.5. L'unità di misura delle due funzioni rappresentate dalla
III.3.9 è M per cui valori negativi di tali funzioni sono privi di significato fisico. Conseguentemente
la soluzione è pNH3 =3.6167.
13
1,e-3
8,e-4
6,e-4
4,e-4
2,e-4
f 0e+0
-2,e-4
-4,e-4
-6,e-4
-8,e-4
-1,e-3
3,608
3,610
3,612
3,614
3,616
3,618
pNH3
Fig. III.5. Soluzione grafica della III.3.9.
Conseguentemente si trova
[Ag+]=10-2.3858
[Ag(NH3)+]=10-2.6825
[Ag(NH3)2+]=10-2.4192
[NH4+]=10-4.1994
[H3O+]=10-9.8327 (pH=9.83)
[OH-]=10-4.1673
Dal DL di fig.III.3 la soluzione al problema si ottiene ponendo
[Ag+] = [Ag(NH3)2+] + [NH3]
14
che porta a pNH3 = 3.61. La coincidenza tra i valori trovati con i due approcci, quello numerico
(rigoroso) e quello ottenuto dal DL, indica che il secondo, nel caso in oggetto rimane
sufficientemente accurato.
Qualora si operi a pH costante la trattazione analitica è molto semplificata ovvero l'uso del DL
diviene in generale rigoroso con l'introduzione delle costanti condizionali. Definendo la
concentrazione di legante non impiegato nei complessi amminici, [NH3'] come:
[NH ] = [NH ] + [NH ] = C
'
3
+
4
3
NH 3
[
] [
− Ag ( NH 3 ) − 2 Ag ( NH 3 )2
+
+
]
(III.3.10)
si può scrivere
[NH ]=[NH ]1+ [HKO ]
+
'
3
3
3


a
NH 3' K a
NH 3 =
K a + H 3O
= NH 3' α NH 3
+
(III.3.11)
(III.3.12)
A pH tamponato α NH 3 ha un valore costante per cui dall'equazione di β1
[Ag (NH ) ]
+
β1 =
3
[Ag ][NH ]α
+
'
3
(III.3.13)
NH 3
si ottiene
[Ag (NH ) ]
=
+
β = β1α NH
'
1
3
3
[Ag ][NH ]
+
'
3
(III.3.14)
dove β 1' è la costante condizionale del complesso [Ag(NH3)+] al pH fissato. Analogamente si scrive:
β2 =
[Ag (NH ) ]
+
3 2
' 2
2
3
NH 3
[Ag ][NH ] α
+
(III.3.15)
da cui
15
2
β 2' = β 2α NH
=
3
[Ag (NH ) ]
+
3 2
[Ag ][NH ]
' 2
3
+
(III.3.16)
Come esempio è di seguito riportato, in fig. III.6, il DL relativo al sistema in oggetto calcolato a pH
7 per una concentrazione 10-2 M di Ag. Dato che a pH 7 si ha
1
α NH 3 =
1+
H 3O +
Ka
=
1
= 10 −2.25
−7
10
1 + −9.25
10
le costanti condizionali diventano K1'=101.07 e K2'=101.64. Un confronto con il DL di fig.III.3 mostra
uno spostamento del sistema a sinistra e cioè verso una destablilizzazionme dei complessi a seguito
della minore quantità di ammoniaca disponibile a pH 7 rispetto a pH 9.8.
16
pNH3'
0
0
1
2
3
4
5
6
-1
[Ag+]
log [Ci]
-2
-3
']
H3
[N
-4
)+ ]
H3
N
g(
[A
+]
)
3 2
(NH
[Ag
-5
-6
Fig.III.6. DL del sistema Ag+/NH3 a pH 7. CAg = 10-2 M, log K1' = 1.07, log K2' = 1.64.
17
4. Complessi chelati
L'uso di agenti complessanti polidentati (chelanti) in chimica analitica è di particolare rilievo per un
duplice motivo:
i) le costanti di formazione sono elevate
ii) sono assenti complessi intermedi a differenza di quanto ha luogo con leganti monodentati.
Questa circostanza è dovuta al fatto che un singolo legante "satura" la coordinazione dell'accettore
formando anelli di atomi di particolare stabilità grazie all'assenza di distorsione dei legami
interatomici. Ne consegue un più alto grado di complessazione a parità di legante libero
all'equilibrio ed un minore effetto della diluizione sulla stabilità del complesso.
Tra gli agenti chelanti, di particolare rilevanza è l'acido etilendiamminotetracetico (EDTA, H4Y)
che dà, con numerosi metalli, complessi con stechiometria 1:1 la cui stabilità dipende fortemente
dal pH della soluzione.
EDTA: pK1=2.0, pK2=2.67, pK3=6.16, pK4=10.26.
Per il complesso MY(m-4)+ le equazioni che descrivono il sistema sono:
M
m+
K1 =
K2 =
K3 =
4-
+ Y
(m-4)+
↔ MY
H 3Y − ⋅ H 3O +
H4Y
H 2 Y 2 − ⋅ H 3O +
H 3Y −
HY 3− ⋅ H 3O +
H 2 Y 2−
β MY =
MY ( m− 4) +
M m+ Y 4 −
(III.4.1)
(III.4.2)
(III.4.3)
(III.4.4)
18
Y 4 − ⋅ H 3O +
K4 =
(III.4.5)
HY 3−
Y ' = C Y − MY ( m−4) +
(III.4.6)
Y ' = Y 4 − + HY 3− + H 2 Y 2 − + H 3Y − + H 4 Y
(III.4.7)
Si noti come la combinazione della III.4.6 con la III.4.7 rappresenti il bilancio di massa di Y.
Riscrivendo la III.4.7 come [Y'] = [Y4-]/αY4- la III.4.1 diviene
β MY =
MY ( m− 4) +
M m+ ⋅ Y ' ⋅ α
(III.4.8)
Y4 −
da cui
β 'MY
=α
Y4 −
⋅ β MY =
MY ( m− 4) +
M m+ Y '
(III.4.14)
che fornisce la dipendenza della costante condizionale del complesso dal pH. Il grafico relativo al
sistema Ni2+/EDTA (logβNiY = 18.6) è riportato in figura III.7. Si notano 5 zone in cui la pendenza è
progressivamente decrescente fino a divenire nulla. Esse corrispondono al diverso numero di
protoni rilasciati all'atto della formazione del complesso tra ione metallico ed EDTA variamente
protonato per cui in ambiente fortemente acido la pendenza è 4 mentre in ambiente alcalino la
pendenza è 0. In questa zona costante condizionale e costante termodinamica coincidono.
19
20
15
log β'
10
5
0
-5
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
pH
Fig.III.7. Andamento della costante condizionale del complesso NiY2-. Le verticali
corrispondono ai valori delle quattro pK dell'EDTA: pK1=2.0, pK2=2.67, pK3=6.16,
pK4=10.26. Il valore costante di β' per pH >> 10.26 coincide con il valore
termodinamico, β = 1018.6.
In fig.III.8 sono riportati analoghi diagrammi per altri complessi metallo-EDTA.
20
log β'
25
Fe3+
20
Cu2+
Ni2+
Zn2+
15
Fe2+
Ca2+
10
Mg2+
Ba2+
5
0
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
pH
Fig.III.8. Andamento delle costanti condizionali di vari complessi metallo-EDTA. Le
verticali corrispondono ai valori delle quattro pK dell'EDTA.
Oltre al legante anche l'accettore può essere soggetto ad equilibri competitivi ed anche in questo
caso l'uso della costante condizionale può essere conveniente. Consideriamo la formazione del
complesso MY in ambiente ammoniacale in cui M forma complessi anche con NH3. Omettendo le
cariche per semplicità
C M = M ' + MY
(III.4.15)
n
M ' = M + ∑ β i M NH 3
i
(III.4.16)
1
[M ] = [M ']
1

i 
1 + ∑ β i [NH 3 ] 
1


n
= [M '] ⋅ α M
(III.4.17)
21
β MY =
MY
M ⋅ Y
4−
=
MY
M ⋅ Y ⋅αM ⋅α
'
β 'MY = β MY ⋅ α M ⋅ α Y4 − =
'
(III.4.18)
Y4 −
MY
M' ⋅ Y'
(III.4.19)
Si noti che il valore di β 'NiY ricavato contiene ora due termini "α", uno dipendente dal pH l'altro
dalla concentrazione di NH3. L'esistenza di equilibri competitivi a carico dell'accettore può causare
un andamento a massimo della costante condizionale in funzione del pH. Questa situazione si
verifica tipicamente quando l'accettore forma idrosso complessi al crescere del pH.
5. Titolazioni complessometriche
5.1 Introduzione.
Nelle titolazioni complessometriche si fa uso pressochè esclusivo di leganti chelanti per conseguire
quei vantaggi sopra ricordati e cioè una stechiometria ben definita (normalmente 1:1) ed elevate
costanti di formazione dei complessi. Poichè nel corso della reazione di titolazione l'agente
chelante, ad esempio l'EDTA, viene di solito introdotto in soluzione nella forma parzialmente
protonata H2Y2- la reazione globale di formazione del complesso è
M m+ + H 2 Y 2 − + 2 H 2 O ↔ MY ( m−4) + + 2 H 3 O +
Durante il decorso della titolazione si ha rilascio di protoni con conseguente diminuzione del pH per
cui si configura una situazione in cui la costante condizionale della reazione di titolazione tende a
diminuire con continuità. Di qui la necessità dell'uso di tamponi per bloccare il pH durante la
titolazione e mantenere costante il valore della β'. L'eventuale azione complessante che l'anione del
tampone può esplicare nei confronti del metallo da titolare è di aiuto se il catione metallico tende a
precipitare in ambiente alcalino, ma comporta inevitabilmente una diminuzione della costante
condizionale.
5.2 Curva di titolazione.
Nel caso di una titolazione tra uno ione Mm+, C0 M, con l'anione dell'EDTA, Y4-, C M, ha luogo la
reazione:
22
M m+ + Y 4 − ↔ MY ( m−4) +
Facendo uso della notazione delle costanti condizionali ed omettendo le cariche le specie coinvolte
sono formalmente M', Y' e MY dove le prime due rappresentano la somma di tutte le specie di M e
di Y non contenute nel complesso. Ne consegue che
β' =
MY
M ' Y'
(III.5.1)
M ' + MY =
C 0 V0
V + V0
(III.5.2)
Y ' + MY =
CV
V + V0
(III.5.3)
Per definizione la frazione titolata è
Φ=
CV
C 0 V0
(III.5.4)
per cui sottraendo membro a membro la III.5.2 e la III.5.3 e dividendo per
([M '] − [Y '])V + V0 =1 − Φ
C 0V0
C 0 V0
si ottiene
V + V0
(III.5.5)
Questa, tramite la costante condizionale ed il bilancio di massa sul metallo diviene in successione

[MY ] 1  V + V0
Φ=1 −  [M '] −
[M '] β '  C0V0

(III.5.6)
C 0V0


− [M '] 

V + V0
1  V + V0
Φ = 1 −  [M '] −

[M '] β '  C0 ⋅V0




(III.5.7)
che è l'equazione rigorosa della curva di titolazione.
Nel diagramma pM' vs. Φ si può notare quanto segue
23
Φ = 0.
M' = C0
(III.5.8)
Φ < 1.
Prima del P.E. può essere trascurato [Y'] e pertanto
Φ = 1 − M'
V + V0
C 0 V0
(III.5.9)
Φ > 1.
Dopo il P.E. può essere trascurato [M'] per cui
V + V0
C 0 V0
(III.5.10)
MY V + V0
M ' β ' C 0 V0
(III.5.11)
Φ = 1 + Y'
Φ = 1+
Se la reazione è quantitativa è accettabile l'approssimazione
MY =
C 0 V0
V + V0
(III.5.12)
per cui la III.5.11 diviene
Φ = 1+
1
M' β '
Arrestando la titolazione a Φ = 2 la quota finale è M' =
(III.5.13)
1
che evidenzia come l'escursione del
β'
pM' dipenda oltre che dalla concentrazione iniziale anche dal valore di β'. Ponendo Φ =1 nella
III.5.5 si ottiene la condizione del P.E.
[Y'] = [M'].
(III.5.14)
24
Se Φ ≈ 1 e la reazione è sufficientemente quantitativa (β' elevata) [M'] risulta trascurabile nei
confronti della concentrazione analitica per cui dalla III.5.7 si ottiene
C 0V0




V + V0 1  V + V0

Φ = 1 − [M '] −

[M '] β '  C0V0




(III.5.15)
In particolare per Φ = 1 e diluizione trascurabile
M'
P.E.
C0
M'
P.E.
=
=
1
β' M '
(III.5.16)
P.E.
C0
β'
(III.5.17)
La relazione III.5.14 è ottenibile direttamente anche da un bilancio di legante analogo al bilancio
protonico degli equilibri acido base. Sotto la condizione di totale completezza della reazione il
complesso MY rappresenterebbe la sola specie presente al P.E. della titolazione per cui
assumendolo come livello 0 si può scrivere:
+1
M'
↑
0 − − − − − MY 2−
↓
−1
Y'
e dalla III.5.1 si riottiene immediatamente la III.5.17 per diluizione trascurabile. Si noti che qualora
si desideri passare dalla curva pM' vs. Φ alla pM vs. Φ, analoga alla curva sperimentale ottenibile
per via potenziometrica, è sufficiente calcolare M' · α
M m+
.
5.3 Individuazione del P.F.. Scelta dell'indicatore e del pH.
Oltre che alle metodiche strumentali quali la spettrofotometria, la monoamperometria, ecc., il P.F.
delle titolazioni complessometriche si determina facendo uso di indicatori cromatici come il Nero
Eriocromo T (EBT) o il piridilazonaftolo (PAN) ed altri. Il principio di funzionamento di questi
25
indicatori è la competizione tra l'indicatore, anch'esso complessante per il metallo, ed il titolante, di
solito l'EDTA. In difetto di EDTA (Φ < 1), il metallo è disponibile alla formazione del complesso
con l'indicatore e la soluzione assume il colore del complesso M-In mentre per Φ > 1 tutto il metallo
è sequestrato dall'EDTA e la soluzione assume la colorazione propria dell'indicatore libero. Di qui
l'esigenza che la costante di formazione di M-In sia inferiore a quella di M-EDTA. Poiché sia
l'EDTA che l'indicatore sono coinvolti in equilibri acido-base, caratterizzati da costanti diverse, la
scelta del pH a cui condurre la titolazione può essere critica. Occorre individuare preliminarmente
il limite inferiore di pH sotto il quale il valore di β' è troppo piccolo cioè quando la reazione non è
più quantitativa. Convenzionalmente tale limite corrisponde ad una completezza pari a 99.9% nella
formazione del complesso con una presenza di legando libero dello 0.1%. Dalla III.5.1 deve essere
quindi
β' =
0.999
(0.001)2 C0
(III.5.18)
β ' C 0 = 10 6
26
24
22
20
log β
18
16
14
12
10
8
6
0
2
4
6
8
10
pH
Fig.III.9. Valore minimo di pH per la quantitatività della titolazione complessometrica con EDTA di
12 metalli in concentrazione C0 = 10-2 M. I metalli sono: Fe3+, Hg2+, Cu2+, Ni2+, Pb2+, Cd2+, Zn2+,
Co2+, Fe2+, Mn2+, Ca2+, Mg2+, Sr2+ elencati in ordine decrescente di β.
26
Individuato il limite inferiore di pH oltre il quale la titolazione non è fattibile (vedi fig. III.9), in
base all'indicatore scelto occorre individuare il pH ottimale. Esso è quello per cui il P.F. (viraggio
dell'indicatore) è il più prossimo possibile al P.E.. Come nel caso degli indicatori acido-base, il
viraggio dell'indicatore ha luogo tra
MIn
In ' M '
M'
P.F.
MIn
MIn
MIn
1
= 10 e
=
con P.F. teorico a
= 1. Da
In'
In'
10
In'
= β 'MIn si ottiene
P.F.
=
1
β 'MIn
(III.5.19)
Il pH ottimale è quello per cui [M']P.E. = [M']P.F.
L'approccio grafico utilizzato più volte nella risoluzione di equazioni di ordine superiore risulta
particolarmente conveniente anche in questo contesto. Dovendo valere in assenza di diluizione le
III.5.17 e III.5.19
M'
=
P.E.
M'
P.F.
=
C0
β 'MY
1
β 'MIn
il P.F. coincide con il P.E. allorchè
1
β 'MIn
=
C0
β 'MY
(III.5.20)
Diagrammando il logaritmo di III.5.17 e III.5.19 contro il pH il punto di incontro delle curve
fornisce il pH ricercato. La fig.III.10. riporta il caso della titolazione dello ione Mg2+ con EDTA (β
= 108.7) usando come indicatore l'EBT (β = 107).
27
8
6
2+ ] P.E
4
2
f=
.
g
[M
g
- lo
0
.F .
-2
g[
M
g 2+
]P
f
f=
-6
-lo
-4
-8
pH = 9.6
-10
-12
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
pH
Fig. III.10. Determinazione grafica del pH ottimale per la titolazione di Mg2+ 10-2 M con
EDTA, indicatore EBT.
28
6. Esempi di risoluzione di esercizi.
Esercizio n.1. A 25 ml di soluzione di acido imminodiacetico (H3X+) 0.12 M, tamponata a pH = 7,
si aggiungono 25 ml di Cu2+ 0.05 M. Calcolare la concentrazione di Cu2+ nella soluzione risultante.
Per H3X+ : pK1 = 1.82, pK2 = 2.84, pK3 = 9.79
Per Cu 2 + + 2 X 2 − = CuX 22 −
log β 2 = 16.5
Metodo algebrico.
A seguito della diluizione le concentrazioni analitiche sono: CH3X+ = 0.06 M e CCu = 0.025 M. Le
specie presenti in soluzione sono: H3X+, H2X, HX-, X2-, Cu2+, CuX22- per un totale di 6. Si imposta
quindi un sistema di 6 equazioni:
CCu= [Cu2+] + [CuX22-]
(III.3.32)
C H X+ = 2 CuX 22 − + H 3 X + + H 2 X + HX − + X 2 −
3
(III.3.33)
CuX 22 −
Cu
2+
X
= β2
(III.3.34)
= K1
(III.3.35)
= K2
(III.3.36)
2− 2
H 2 X H 3O +
H 3X +
HX − H 3O +
H2X
X 2 − H 3O +
HX −
= K3
(III.3.37)
La combinazione di queste equazioni porta a
[
C H X + =2 CuX
3
2−
2
]+ [X ] [
2−
] [
] [
]
+ 2
+ 3 
 H O+
H
O
H
O
3
3
3
1+

+
+


K
K
K
K
K
K
3
3
2
3
2
1


(III.3.38)
Ricavando dai due bilanci di massa [CuX22-] e uguagliando si ha
29
(
0 .5 C H
3X
+
[ ]
)
[
− X 2− α X−12 − = CCu − Cu 2+
]
(III.3.39)
La concentrazione di X2- può essere data in funzione di [Cu2+]
C Cu − Cu 2 +
Cu
X
2+
2−
X
=
2− 2
= β2
(III.3.40)
C Cu − Cu 2 +
(III.3.41)
Cu 2 + β 2
da cui
[Cu ] = C
2+
Cu
[

CCu − Cu 2+
− 0.5 C H X + − α X−12−
 3
Cu 2+ β 2

[
]
] 


(III.3.42)
Una facile risoluzione di questa equazione si ha per via grafica, vedi fig.III.11, ricavando [Cu2+]
dall'incrocio di
y = [Cu2+]
(III.3.43)
e
[

CCu − Cu 2+
y = CCu − 0.5 C H X + − α X−12−
 3
Cu 2+ β 2

[
]
] 


(III.3.44)
30
-4,790
-4,790
-4,790
y
-4,791
-4,791
-4,791
8,5200
8,5205
8,5210
8,5215
8,5220
log [Cu2+]
Fig. III.11. Soluzione grafica dell'eq. III.3.42.
Si trova log [Cu2+] = -8.5.
Metodo grafico
Facendo uso della costante condizionale la soluzione può essere ottenuta per mezzo di un DL
log[Ci] vs. pX' relativo al sistema equivalente CuX22- 0.025 M e X2- 0.01 M. A pH 7 α −12 − = 617
X
per cui β '2 = 8. 2 1010 e X = X 2 − 617 . Il punto sistema ha come ascissa un valore di log[Ci] =
'
logCCu tale per cui [CuX22-]/[ Cu2+]=1. Ne consegue
2−
1 CuX 2
β '2
Cu
2+
= X ' = 3.14 10 −6 ; pX ' = 5. 4
31
e
log CCu = log 0.025 = -1.6
L'andamento di Cu2+ è dato da:
[
][
](
] [
[ ])
CCu = CuX 22− + Cu 2+ = Cu 2+ 1 + 8.21010 X '
2
(III.3.45)
C Cu
log Cu 2 + = log
1 + 8. 2 1010 X '
(III.3.46)
2
da cui si individuano due zone rettilinee:
i) per 1 >> 8.2 1010 [X']2, cioè per [X'] << 3.5 10-6
log [Cu2+] = log CCu
(III.3.47)
ii) per 1 << 8.2 1010 [X']2, cioè per [X'] >> 3.5 10-6
log [Cu2+] = log CCu - 10.9 - 2 log [X']
(III.3.48)
Analogamente, per CuX22- si può scrivere:

] [CuX ] = [CuX ]1 + 1
β [X ]
 8.210 [X ]
[
CCu = CuX 22− +
2−
2
' 2
'
2
2−
2
10

1
log CuX 22− = log CCu − log1 +
 8.21010 X '

[
]
[ ]
2
'


2 





(III.3.49)
(III.3.50)
Le due zone approssimabili a delle rette si hanno:
i) per 1 >>
1
8. 2 1010 X
' 2
, cioè per [X'] >> 3.5 10-6
32
log [CuX22-] = log CCu
(III.3.51)
1
ii) per 1 <<
8. 2 1010 X
' 2
, cioè per [X'] << 3.5 10-6
log [CuX22-] = log CCu + 10.9 + 2 log [X']
(III.3.52)
Il DL è mostrato in fig.III.12.
pH
0
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
[CuX22-]
[Cu2+]
-2
log [Ci]
-4
-6
-8
-10
2-
[X
]
-12
-14
Fig. III.12. DL del sistema CuX22- 2.5 10-2 M
Analogamente al bilancio protonico si imposta un bilancio di legante pensando che all'inizio tutto il
Cu sia sotto forma di complesso e che ci sia del legante in eccesso in ragione di 10-2 M.
33
Cu 2+
+2
↑
+1
10 − 2
/
↑
↑
0 − − − − − CuX
−1
2−
2
− − − − − 10 − 2 X 2−
↓
↓
X'
X'
da cui
2 [Cu2+] + 10-2 = [X']
Dal DL si vede che 2 [Cu2+] è trascurabile rispetto a 10-2 e pertanto a [X'] = 10-2 si trova log [Cu2+]
= -8.5 come in precedenza.
Esercizio n.2: si debba titolare Zn2+ 10-1 M con EDTA usando il Ditizone (HIn) come indicatore.
Valutare il pH ottimale di lavoro e, sotto queste condizioni, gli errori teorici agli estremi
dell'intervallo di viraggio dell'indicatore.
per H 4 Y : pk 1 = 2 . 0 ,
per HIn : pK In = 4. 6 ,
pk 2 = 2 . 7 , pk 3 = 6. 2 , pk 4 = 10. 3
β ZnY = 1016 , β ZnIn = 105.2
Risoluzione
In assenza di diluizione e per reazione di complessazione quantitativa vale
Zn 2 +
αY =
P.E.
[Y ]=
10 −1
1016 α Y
=
(III.3.53)
4−
[Y ']
1 + 10
10.3
[H O ] + 10 [H O ]
+
3
+ 2
16.5
3
1
+ 10
19.2
[H O ]
+ 3
3
+ 10
21.2
[H O ]
(III.3.54)
+ 4
3
e
Zn 2 +
P . F.
=
1
10 −5.2 α In
(III.3.55)
34
α In =
In −
In '
=
1
1 + 10
4.6
(III.3.56)
H 3O +
Diagrammando [Zn2+]P.E. e [Zn2+]P.F. vs. pH il punto di incontro fornisce il pH ottimale in cui
coincidono [Zn2+]P.E. e [Zn2+]P.F.. Tale valore è dato dal diagramma di fig.III.13.
4
2
log [Zn2+]
0
-2
-4
[Zn2+]P.F.
-6
-8
[Zn2+]P.E.
pH = 4.65
-10
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
pH
Fig. III.13. Determinazione grafica del pH ottimale per la titolazione di Zn2+ 10-1
M con EDTA ed indicatore ditizone.
Per il pH trovato deve essere ora verificata la validità dell'assunzione iniziale, cioè della
quantitatività della reazione. A tale scopo si calcola la β 'ZnY a quel pH e si controlla se
(β )
'
ZnY ott
10 −1 >10 6
(III.3.57)
35
(
'
A pH = 4.65 αY = 107.22 e β ZnY
)
ott
10 −1 = 10 7.78 >10 6 per cui la reazione è quantitativa. Il valore di
[Zn2+] agli estremi del viraggio si trova introducendo i rapporti
ZnIn +
In '
ZnIn +
In
'
= 10
errore in difetto
1
10
errore in eccesso
=
e
(III.3.58)
(III.3.59)
nella espressione della costante dell'indicatore.
β 'Ind
=
Zn 2 +
Zn 2 +
ZnIn +
≅ 10
Zn 2 + In '
P . F.
P . F.
10
=
=
'
β Ind
4.9
→
Zn
2+
=
ZnIn +
(III.3.60)
β 'Ind In '
= 10 −3.9
1
10 β 'Ind
(III.3.61)
= 10 −5.9
(III.3.62)
I valori di [Zn2+]P.F. così calcolati, una volta introdotti nella espressione della curva di titolazione

1
Φ −1 =  '
2+
 β ZnY Zn
[
] (C
P. F .
Zn
[
− Zn 2+
] ) − [Zn ]
2+
P. F .
P. F .
 1

 C Zn
(III.3.63)
consentono il calcolo dei corrispondenti errori. Si trova
εdifetto = -1.25 10-3
εeccesso = 5.93 10-5.
Esercizio n.3: Stabilire la concentrazione minima di [Hg2+] che si può titolare con EDTA ed
indicatore blù-nero eriocromo B a pH = 10 con un errore teorico inferiore ad 1 %.
per H 4 Y : pk 1 = 2 . 0 , pk 2 = 2 . 7 , pk 3 = 6. 2 , pk 4 = 10. 3
per H 2 In : pk 1 = 6. 2 ; pk 2 = 12. 5
per HgY : lg β = 8. 7 ; HgIn = lg β = 7 . 4
36
Risoluzione
Si calcolano la costante condizionale β 'HgY a pH = 10 che risulta essere
β 'HgY
=
β HgY
HgY 2 −
=
αY
Hg
2+
Y
= 108.22
'
(III.3.64)
e la costante condizionale β 'HgIn
β 'HgIn
=
β HgIn
HgY 2 −
=
α In
Hg
2+
In
'
= 10 4.9
(III.3.65)
Al P.F. della titolazione si ha
[Hg]P.F. = 10-4.9
(III.3.66)
In assenza di diluizione si può scrivere
([
] [ ]) C1
1 − Φ = Hg 2+ − Y '
(III.3.67)
0
e dato che
Y =
'
HgY 2 −
Hg
2+
1
(III.3.68)
β 'HgY
HgY 2 − = C 0 − Hg 2 +
(III.3.69)
si ottiene

2+
 Hg

[
]
P. F .
−
β
'
HgY
1
Hg 2+
[
 1
(
<10
C −[Hg ] )
]
 C
2+
0
P. F .
P. F .
−2
(III.3.70)
0
C 0 > 1. 2 10 −3
37
Esercizio n.4: Si consideri la titolazione di [Bi3+] e [Pb2+] 10-2 M ciascuno, con EDTA a pH = 2 e
pH = 5, usando sempre come indicatore arancio xilenolo. Verificare le potenzialità del
procedimento ai pH considerati. Si trascurila diluizione.
per EDTA : pk 1 = 2 . 0 , pk 2 = 2 . 7 , pk 3 = 6. 2 , pk 4 = 10. 3
log β BiY = 22 . 8
log β PbY =18
a pH 2: log β 'BiIn = 5. 4
; log β 'PbIn = − 0. 2
a pH 5: log β 'BiIn =13.1 ; log β 'PbIn = 7. 0
Risoluzione
Prima di tutto si devono trovare le costanti condizionali dei complessi con l'EDTA a pH 2 e pH 5
calcolando gli αY. Si trova
(α Y ) pH =2 = 2.810 −14
(α Y ) pH =5 = 2.96 10 −7
(β
(β
(β
(β
)
)
)
)
'
BiY pH = 2
'
=1.76109 , lg β BiY
=9.2
'
BiY pH =5
'
=1.861016 , lg β BiY
=16.2
'
PbY
pH = 2
'
= 2.810 4 , lg β PbY
= 4 .4
pH =5
'
= 2.961011 , lg β PbY
=11.5
'
PbY
La conoscenza delle costanti condizionali MInd permette di calcolare i diversi [M]P.F. A pH 2 si ha
[Bi3+]P.F. = 10-5.4
mentre per il Pb2+ l'indicatore non opera. A pH = 5
[Bi3+]P.F. = 10-13
[Pb2+]P.F. = 10-7
Si può dire quindi che a pH 2 la soluzione vira per [Bi3+] = 10-5.4 mentre a pH = 5 la soluzione vira
per [Bi3+] = 10-13. Introducendo nell'equazione della curva di titolazione i valori delle
38
concentrazioni corrispondenti a questi due P.F. si calcolano i corrispondenti valori di Φ e quindi gli
errori
([Y ]− [Bi ]− [Pb ]) 2C1
'
3+
2+
= Φ −1
0
Dalla fig.III.14a [Bi3+]P.F. = 10-5.4 si trova
PbY 2 − = 10 −3.4
Pb 2 + = 10 −2 − 10 −3.4 = 9 . 6 ⋅ 10 −3
Y ' = 10 −5.7
che inseriti nell'equazione sopra riportata danno Φ=0.52. Ricordando la definizione di Φ il valore
trovato indica che a pH 2 si titola solo il Bi con un errore in eccesso del 4 %. Analogamente dalla
fig.III.14b si ricavano le concentrazioni corrispondenti a [Pb2+]P.F. = 10-7 e [Bi3+]P.F. = 10-13. Poichè
la condizione [Pb2+]P.F. = 10-7 richiede meno [Y']P.F. che non la condizione [Bi3+]P.F. = 10-13 è
necessario fare riferimento a quest'ultima. Si ottiene
BiY − =10 −2
Pb 2 + = 10 −8.8
Y ' = 10 −4.15
che danno per la somma Bi 3+ + Pb 2 + un errore in eccesso dello 0.35 %.
39
pY'
0
5
10
15
20
-
iY
[B
-5
[P
b
2+
]
0
[B
i 3+
]
2-
]
log [Ci]
]
bY
[P
-10
1° P.E.
']
[Y
2°P.E.
-15
-20
pY'
0
0
5
10
15
20
-
iY
[B
-15
]
2+
2° P.E.
']
[Y
[B
i 3+
]
[P
b
1° P.E.
]
log [Ci]
2-
bY
[P
-10
]
-5
-20
Fig.III.14. DL per il sistema Bi3+, Pb2+ 10-2 M - EDTA; a) pH 2; b) pH 5.
40