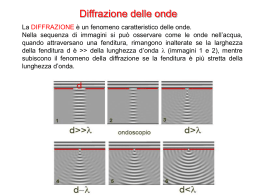
Intensità figura di diffrazione da una fenditura
φ=0
Si suppone di avere la fenditura divisa in un gran numero di
piccole strisce di larghezza ∆y. Ogni striscia si comporta
Come una sorgente di radiazione coerente e in un punto P
dello schermo dà un contributo ∆E al campo elettrico totale.
Il campo elettrico totale in P è dato dalla somma dei
Contributi di tutte le strisce. I contributi di due strisce
adiacenti sono sfasati di ∆φ=(2π/λ)∆y senθ.
Per piccoli valori di θ si può ipotizzare che I valori di ∆E
siano uguali per ogni striscia.
Quando θ=0 i contributi ∆E sono allineati e E0=N∆E, N strisce
In b) si ha ER (lunghezza corda)per un certo angolo θ, ΕR<E0.
La differenza totale di fase tra le onde provenienti dai due
Estremi della fenditura è:
2π
2π
φ = NΔφ =
λ
NΔysenθ =
λ
asenθ
Aumentando θ la catena dei vettori forma ad un certo punto
un percorso chiuso, quindi a somma nulla  ER=0, primo
minimo:
€
2π =
Ettore Focardi
2π
λ
asenθ →senθ =
λ
a
1
€
Intensità figura di diffrazione da una fenditura(2)
Si possono ottenere l’ampiezza totale del campo ER e l’intensità della luce I in ogni punto P
Sullo schermo considerando il caso in cui ∆y0 e N∞. In questo limite la catena dei vettori
Dalle singole strisce è la curva continua rossa. La lunghezza dell’arco è E0.
Per un generico θ si ha:
φ
Rsen
2
= E R /2
Ma E0=Rφ, quindi
€
φ/2
sen
E R = 2Rsen
φ
E
φ
= 2( 0 )sen = E 0 [
φ
2
φ
2
2
φ
2]
Poichè nel punto P dello schermo l’intensità totale I ∝ ER2 è
φ
€
Minimi per
πasenθ
λ
= mπ o senθ = m
λ
a
€
2
⎡
φ ⎤ €
⎢ sen 2 ⎥
I = Imax ⎢
φ ⎥
⎢
⎥
⎣ 2 ⎦
€
Imax intensità a θ=0
⎡ sen(πasenθ / λ) ⎤ 2
I = Imax ⎢
⎣ πasenθ / λ ⎥⎦
φ/2
m = ±1,±2,...
Ettore Focardi
2
Risoluzione di una fenditura
La capacità degli strumenti ottici di distinguere oggetti vicini tra loro è limitata dalla natura
Ondulatoria della luce. Due sorgenti di luce si trovano a grande distanza da fenditura larga a.
Per la diffrazione, l’imagine di ogni sorgente
Consiste di una regione centrale luminosa con
Frange laterali meno intense chiare e scure.
Sullo schermo si osserva la somma delle due
Figure di diffrazione. Se S1 e S2 sono distanti
Tra loro, I loro massimi centrali non si
Sovrappongono, immagini distinte, risolte.
Se sono vicine, I due massimi si sovrappongono,
Le immagini non sono risolte.
Criterio di Rayleigh : Le immagini sono considerate risolte se il massimo centrale di una
coincide con il primo minimo dell’altra.
λ
λ<<a, senθ∼θ  θmin=λ/a
senθ =
a
Molti strumenti ottici utilizzano aperture circolari, in questo
caso si trova
θmin=1.22 λ/D D=diametro apertura
€
Ettore Focardi
3
esempi
1) Risoluzione limite di un microscopio.
Per osservare un oggetto al microscopio viene usata luce di λ=589 nm. Se l’apertura
dell’obbiettivo ha diametro 0.9 cm, trovare l’angolo limite di risoluzione.
θ min
⎛ 589⋅ 10 −9 m ⎞
−5
= 1.22⎜
⎟ = 7.98⋅ 10 rad
−2
⎝ 0.9⋅ 10 m ⎠
Due punti che sottendono all’obbiettivo un angolo minore non sono distinti
€ Si calcoli per l’occhio l’angolo limite di risoluzione, limitandoci
2)Risoluzione dell’occhio.
alla sola diffrazione.
Utilizziamo luce di λ=500 nm e diametro pupilla di 2 mm.
θ min
⎛ 500⋅ 10 −9 m ⎞
λ
−4
= 1.22 = 1.22⎜
⎟ = 3⋅ 10 rad
−3
D
⎝ 2⋅ 10 m ⎠
Con questo risultato si determina la separazione minima d
€
tra due sorgenti puntiformi che l’occhio puo’ distinguere a distanza L.
senθ min ~ θ min =
d
L
d = Lθ min
Se L=25 cm è d=(25 cm)(3 10-4 rad)=8 10-3 cm spessore di un capello!!!
€
Ettore Focardi
4
Reticolo di diffrazione
Il reticolo di diffrazione, utile nell’analisi di sorgenti di luce, consiste in un gran numero di
fenditure parallele equispaziate.
Si puo’ costruire un reticolo a trasmissione incidendo righe || su lastra di vetro. Gli spazi tra le
Righe sono trasparenti alla luce e quindi funzionano come fenditure equispaziate.
Si puo’ costruire un reticolo a riflessione incidendo righe || su superficie materiale riflettente.
La riflessione della luce da parte degli spazi tra le riche è di tipo speculare, mentre la riflessione
Delle righe incise nel materiale è una riflessione diffusa.
I reticoli, hanno una spaziatura fra le fenditure molto piccola (~µm).
Un’onda piana incide ⊥ al piano del reticolo.
Una lente convergente riunisce I raggi in P.
La distribuzione di intensità osservata sullo
Schermo è risultatto di effetti combinati di
Interferenza
€ e diffrazione.
Ogni fenditura produce diffrazione e I fasci diffratti
Inteferiscono tra loro .
Quando lasciano le fenditure le onde hanno la stessa
Fase che sarà diversa quando arrivano in P.
La differenza di cammino tra fenditure adiacenti è
d senθ  d senθ = mλ (m=0,1,2…) max interf
Ettore Focardi
5
Reticolo diffrazione(2)
Si puo’ determinare la lunghezza d’onda, nota la spaziatura del reticolo e l’angolo θ.
Se la radiazione incidente contiene diverse λ per ognuna di esse il massimo di ordine m si trova
ad un angolo specifico. A θ=0 si osservano tutte le λ, si tratta del massimo di ordine zero (m=0).
Il massimo del primo ordine (m=1) si trova ad un angolo dato da senθ=λ/d.
Distribuzione I reticolo da sorgente monocromatica in figura.
Da notare come sono stretti I massimi principali e larghe le
aree scure. Questo aspetto è in contrasto con le larghe frange
Chiare della figura di interferenza.
I reticoli reali hanno molte fenditure per cui I massimi sono
Più evidenti.
Spettrometro a reticolo di diffrazione
Immagine fenditura osservata con un
Microscopio, misurando l’angolo
Si ha informazione della λ.
Ettore Focardi
6
CD reticolo di diffrazione
La luce riflessa dalla superficie di un CD è multicolore.
La superficie di un CD è incisa con un solco a spirale (solchi adiacenti a distanza relativa ~ 1 µm.
La superficie si comporta così come un reticolo a riflessione.
Ogni regione del disco è un reticolo di diffrazione per la luce bianca e riflette colori differenti in
differenti direzioni. Guardando una di queste regioni I colori cambiano spostando la sorgente di
luce, il disco o l’osservatore.
Ettore Focardi
7
Polarizzazione delle onde luminose
Un fascio di luce ordinario consiste in un gran numero di onde emesse dagli atomi costituenti
la sorgente di luce. Ogni atomo produce un’onda con una orientazione particolare del campo
elettrico E, corrispondente alla direzione della vibrazione dell’atomo.
La direzione di polarizzazione di ogni singola onda è definita come la direzione lungo la quale
vibra il campo E,in figura è l’asse y.
Tuttavia una singola onda elettromagnetica può avere il suo vettore E nel
piano yz, in una direzione che forma un qualunque angolo con l’asse y.
Tutte le direzioni di vibrazione sono possibili e quindi l’onda e.m. risultante
è una sovrapposizione delle onde prodotte dalle singole
sorgenti atomiche.
Risultato: onda luminosa non polarizzata (a).
Un’onda è polarizzata linearmente se il campo risultante E vibra
nella stessa direzione in ogni istante (b).
Piano definito da E e da direzione di propagazione è detto
piano di polarizzazione dell’onda. Piano xy nella figura.
È possibile produrre luce polarizzata da luce non polarizzata
eliminando dal fascio tutte le onde tranne quelle i cui vettori E
oscillano in un solo piano..
Ettore Focardi
8
Polarizzazione per assorbimento selettivo
Nel 1938 E.H. Land scoprì un materiale, polaroid, che polarizza la luce mediante assorbimento
selettivo da parte di molecole orientate. Fabbricato in fogli sottili di idrocarburi sottoposti a
tensione in modo da allineare le catene molecolari. Successivamente i fogli sono immersi in una
soluzione contenente iodio con le molecole che diventano conduttrici, con conduzione lungo le
Catene. Perciò le molecole assorbono con efficienza la luce con E || alla lunghezza e trasmettono
Con E ⊥ . La direzione ⊥ alle catene è detta assse di trasmissione.
€
€
Fascio di luce non polarizzata, incidente sulla prima
lamina polarizzatrice, detta polarizzatore. L’asse è
Verticale e quindi la luce trasmessa è polarizzata
Verticalmente. Una seconda lamina polarizzatrice,
analizzatore, con asse che forma θ con
quello del polarizzatore è posta sul fascio.
E0, vettore campo trasmesso.
La componente di E0 || asse analizzatore, E0 cosθ passa. L’intensità del fascio trasmesso
attraverso il polarizzatore è
Legge di Malus
I=Imax cos2 θ
Imax intensità fascio polarizzato su analizzatore
Poichè valor medio di cos2θ è ½, l’intensità della luce che attraversa un polarizzatore ideale
è metà dell’intensità del fascio non polarizzato.
Ettore Focardi
9
€
Polarizzazione per riflessione
Quando un fascio di luce non polarizzata viene riflesso da una superficie, la luce riflessa può
essere completamente polarizzata, parzialmente o non polarizzata a seconda dell’angolo di
incidenza. Se l’angolo e 00 il fascio riflesso è non polarizzato, negli altri casi c’è un po’ di
polarizzazione. Se un fascio di luce non polarizzata incide su di una superficie, I vettori E
possono essere descritti con 2 componenti:
⊥ e || alla superficie. La polarizzazione del fascio
può quindi essere descritta dalle componenti di E
lungo questi assi. La componente || è riflessa più
θ
θp p
intensamente di quella ⊥ fascio parz. polariz.
Facciamo variare l’angolo di incidenza θ1 fino a
€
che angolo tra fascio riflesso e rifratto è 900 (b).
A questo angolo il fascio riflesso è completamente
polarizzato (E||
€ alla superficie).
Angolo di Brewster per riflessione θp.
θp+900+θ2=1800, θ2=900-θp.
usando la legge di Snell della rifrazione con n1=1 n2=n
senθ1 senθ p
n=
=
senθ 2 senθ 2
senθ 2 = sen(90 0 − θ p ) = cos θ p → n = tan θ p
Legge di Brewster
Occhiali da sole fatti con lenti polarizzate riducono il riverbero della luce riflessa. Asse verticale
Ettore Focardi
10
e assorbimento comp. orizzontale