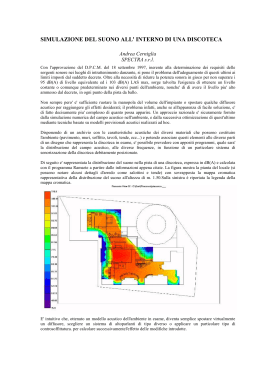
Il suono acustico – capitolo 2
___________________________________________________________________________
Il Suono acustico
Capitolo 2 - Le caratteristiche del suono
Introduzione
pag 1
L’intensità del suono
pag 1
Relazione tra l’intensità sonora e la distanza dalla sorgente
pag 6
L’altezza di un suono
pag 8
Relazione tra frequenza e note musicali
pag 10
Il Timbro di un suono
pag 11
Relazione tra le componenti sinusoidali di un suono periodico complesso
pag 12
Rappresentazione del timbro tramite lo spettro acustico
pag 14
Introduzione
Il suono ha tre caratteristiche: l’intensità, l’altezza e il timbro.
L’Intensità rappresenta la quantità di energia che possiede l’onda di pressione e
pertanto rappresenta l’ampiezza di oscillazione dell’onda.
L’Altezza di un suono è la velocità di oscillazione dell’onda, misurata tramite la
frequenza, e pertanto stabilisce quanto un suono sia acuto (frequenza elevata) o
grave (frequenza bassa).
Il Timbro è quella caratteristica che permette di distinguere i suoni di sorgenti diverse
(ad esempio un flauto in confronto ad una chitarra) sebbene emessi con la stessa
altezza. Rappresenta la forma dell’onda di pressione.
L’intensità del suono
Onde sonore costituite da maggiori differenze della pressione locale hanno ovviamente
un’intensità maggiore pertanto, l’intensità stessa è rapportata al valore della
pressione. Ma qual è l’unità di misura che dobbiamo utilizzare per poter rappresentare
l’intensità delle onde di pressione acustica? Poiché, come abbiamo detto nel capitolo
1, l’unità atmosfera è troppo grande (sarebbe come voler misurare la lunghezza di
una formica utilizzando come unità di misura il chilometro) in realtà se ne utilizza una
molto piccola, derivata, chiamata Pascal (Pa), così definita:
Silvio Relandini 1
Il suono acustico – capitolo 2
___________________________________________________________________________
1 atm = 101.325 Pa
L’onda di pressione acustica che è in grado di indurre nell’uomo la sensazione sonora
di più piccola intensità, ha una variazione di pressione di 20 μPa (ovvero 20
milionesimi di Pa, e circa 5 miliardi di volte più debole della pressione atmosferica),
mentre quella che induce una sensazione sonora di massima intensità (senza produrre
un danno al nostro sistema uditivo), ha una variazione di pressione di 20 Pa. Questo
vuol dire che il nostro sistema uditivo è sensibile ad un intervallo costituito da un
milione di variazioni di pressione.
Rappresentare questo intervallo così ampio tramite un asse lineare non è conveniente
in quanto abbiamo a che fare con un milione di valori e quindi anche se utilizzassimo
un asse lineare lungo un chilometro la distanza tra ogni singolo micropascal sarebbe di
un millimetro!!!
10 Pa
Si ricorre pertanto ad un’altra rappresentazione che utilizza i logaritmi. Quale parola
terribile!!! In realtà il logaritmo può essere considerato un semplicissimo operatore
matematico al pari dell’addizione, sottrazione o moltiplicazione. Sappiamo che
l’esponente e di un numero b non è altro che il numero di volte per cui b viene
moltiplicato per se stesso. Il numero b è detto base.
Esempio:
b = 10, e = 5
be = 105 = 10*10*10*10*10 = 100.000
Il logaritmo invece esegue un calcolo differente, ovvero, dato un numero b (base) e
un numero x, si trova l’esponente e per il quale
be = x
ovvero:
logb x = e
Silvio Relandini 2
Il suono acustico – capitolo 2
___________________________________________________________________________
e sempre riferendoci all’esempio visto sopra
log10 100.000 = 5
in quanto occorre elevare la base 10 all’esponente 5 per ottenere il valore 100.000.
Effettuata questa semplice operazione possiamo calcolare i seguenti logaritmi:
log10 1.000.000 = 6
log10 100.000 = 5
log10 10.000 = 4
log10 1.000 = 3
log10 100 = 2
log10 10 = 1
log10 1 = 0
Ora è possibile costruire il seguente asse logaritmico
Ogni valore della pressione è sempre rappresentabile in maniera semplice anche se
l’asse è piuttosto corto e i rapporti fra i valori non sono più lineari ma esponenziali
(logaritmici). Cosa rappresenta l’asse? Esattamente i valori dell’intensità sonora
espressa come pressione (ovvero la pressione sonora, SPL).
Come si misura l’intensità della pressione sonora? Innanzitutto occorre precisare che
si calcola in realtà un rapporto ovvero il valore di un determinato suono rispetto a
quello di un suono detto di riferimento, che nel nostro caso, coincide con il valore del
suono di intensità più piccola: 20μPa.
Si effettua il seguente calcolo:
P
PR
Silvio Relandini 3
dove appunto PR = 20μPa
Il suono acustico – capitolo 2
___________________________________________________________________________
Come esempio, valutiamo P = 0.2 Pa
0.2 Pa 2 ⋅ 10 −1 Pa
P
=
=
= 10.000
PR 20 μPa 2 ⋅ 10 −5 Pa
ovvero il suono P ha un’intensità 10.000 volte maggiore di PR e se facciamo il
logaritmo di questo rapporto otteniamo:
log 10
P
=4
PR
Per migliorare la leggibilità dei valori e del grafico si moltiplica per un fattore 20 il
logaritmo arrivando così ad un’espressione matematica che rappresenta il decibel
(dB), ovvero uno strumento per la misura dell’intensità di un suono, la cui unità di
misura in realtà rimane il pascal:
dB = 20 log 10
P
PR
Abbiamo così realizzato una scala di intensità della pressione sonora che va da un
valore minimo di 0 ad un valore massimo di 120 dB.
L’intensità sonora può essere espressa anche in Watt (W), ovvero nell’unità della
potenza:
dB = 10 log10
Silvio Relandini 4
W1
W2
Il suono acustico – capitolo 2
___________________________________________________________________________
Considerando che la potenza è proporzionale al quadrato della pressione sonora:
dB = 20 log 10
⎛P
P1
= 10 log 10 ⎜⎜ 1
P2
⎝ P2
2
⎞
W
⎟⎟ = 10 log 10 1
W2
⎠
Pertanto, i famosi valori di riferimento, sia in potenza che in pressione, ricordando che
nel sistema internazionale (SI) la potenza si misura in Watt (W) e la pressione in
Pascal (Pa), sono:
-per la potenza W2 = 10-12 Watt
-per la pressione p2 = 2.10-5 Pascal (che ricordiamo essere una pressione
estremamente piccola, coincidente con la soglia di udibilità dell'orecchio umano).
In pratica, suoni di pressione inferiore non sono neppure udibili.
Vediamo alcuni semplici esempi di applicazione di queste formule.
Es.1 Misurando per una sorgente sonora un’intensità di emissione pari a 0,02 Pa, a
quanti dB corrisponde?
Il calcolo è molto semplice:
0,02 Pa
2 ⋅ 10 −2
L = 20 ⋅ log
dB = 20 ⋅ log
= 20 ⋅ log 1000 = 20 ⋅ 3 = 60dB
20 ⋅ 10 −6
2 ⋅ 10 −5
ovvero, a 0,02 Pa di pressione corrispondono 60dB di livello di pressione sonora.
Es.2 Quanti dB bisogna aggiungere ad un segnale affinchè la sua intensità raddoppi?
Consideriamo il caso in cui l’intensità iniziale sia pari a 0,2 Pa, corrispondente ad un
valore di 80 dB. Dobbiamo calcolare quanti dB deve il segnale quando la sua intensità
è pari a 0,4 Pa.
dB = 20 log10
P1
0,4
= 20 log10
= 20 log 2 = 20 * 0,3 = 6
P2
0,2
Quindi per raddoppiare l’intensità sonora occorre aggiungere 6 dB. Un suono di
intensità pari a 0,4 Pa avrà 86 dB.
Viceversa, quando l’intensità si dimezza occorre togliere 6 dB: ecco che un segnale
pari a 0,1 Pa ha 74 dB.
Silvio Relandini 5
Il suono acustico – capitolo 2
___________________________________________________________________________
Nel caso della potenza sonora:
I dB = 10 log
2W
= 10 log 2 = 10 ∗ 0.3 = 3dB
W
ovvero l’aumento è di 3 dB.
Relazione tra l’intensità sonora e la distanza dalla sorgente
L’intensità sonora ad una certa distanza r dalla sorgente è data dalla formula
I (r ) =
W
4π r 2
e quindi diminuisce di quattro volte per ogni raddoppio della distanza dalla sorgente
(equivalenti a -6 dB tenendo conto che trattasi di misure di potenza).
Come esempio vediamo che succede allontanandoci da un suono che a 3 metri di
distanza dalla sorgente ha un’intensità pari a 90 dB. Osserviamo la seguente tabella:
dB
r
2x
90
1
20
84
2
21
78
4
22
72
8
23
66
16
24
60
32
25
54
64
26
48
128
27
42
256
28
36
512
29
30
1024
210
24
2048
211
18
4096
212
12
8192
213
6
16384
214
0
32768
215
Il suono avrà un’intensità nulla dopo 3*215 metri ossia dopo 98,3 km (dove il termine
3 si riferisce alla distanza iniziale di misurazione dell’intensità dalla sorgente).
Ovviamente questo calcolo è stato effettuato non tenendo conto di altri fenomeni di
assorbimento e di eventuali segnali mascheranti (ovvero in grado di limitare la
percezione del segnale che stiamo misurando). Se ad esempio nell’ambiente fosse
presente un rumore di fondo pari a 60dB, il suono potrebbe non essere più
percepibilea 3*26 ovvero a 192 metri di distanza.
Silvio Relandini 6
Il suono acustico – capitolo 2
___________________________________________________________________________
La tabella seguente mostra i livelli di suono in decibel rilevati da un fonometro:
zanzara vicino all’orecchio
Fruscio di foglie
Bisbiglio (a 1 metro)
Teatro o chiasa vuoti
Rumore di fondo notturno in piccolo centro urbano
Ufficio o ristorante (quieti)
Stadio
Conversazione ad 1 metro
Ufficio o ristorante affollati
Traffico cittadino diurno
Martello pneumatico a 3 metri
Fortissimo fff di grande orchestra in sala
Gruppo rock in un locale chiuso
Schianto di fulmine
Martello su acciaio a 50 centimetri
Jet al decollo a 50 metri
Rottura del timpano
0 dB
10
15
30
35
50
55
50
65
80
90
100
110
110
115
130
160
Vediamo cosa succede quando si hanno invece più sorgenti contemporaneamente.
Supponiamo di avere una formazione orchestrale costituita da 128 elementi ognuno
dei quali, per semplificazione, supponiamo produca un suono di intensità costante pari
a 70 dB. Sappiamo che ogni raddoppio della potenza induce un aumento di 3 dB
pertanto si ha che:
I = 70 + 3 * 7 = 91 dB
In quanto 128 = 27 (7 raddoppi). In generale, date N sorgenti producenti intensità
sonore medie di M decibel, il livello complessivo di intensità è pari a:
n°dB = M + 10 log N
Nel caso dei 128 strumentisti si ha:
n°dB = 70 + 10 log128 = 70 + 21 = 91
Silvio Relandini 7
Il suono acustico – capitolo 2
___________________________________________________________________________
Vediamo nella tabella seguente la potenza massima emessa da alcuni strumenti
musicali e corrispondenti livelli in dB delle intensità rilevate all’aperto a 3 m di
distanza:
strumento
clarinetto
corno
flauto
Voce femminile
Voce maschile
chitarra
oboe
violino
contrabbasso
fagotto
tuba
tromba
pianoforte
trombone
organo
timpani
orchestra
Potenza massima
in uscita (W)
0,05
0,05
0,06
0,09
0,14
0,14
0,18
0,18
0,18
0,18
0,20
0,50
1,1
6
18
25
70
Livello di
Intensità dB
86,5
86,5
87
89
91
91
92
92
92
92
92,5
96,5
100
107
112
113,5
118
L’altezza di un suono
Come abbiamo detto è quella caratteristica grazie alla quale è possibile distinguere
suoni acuti da suoni gravi e corrisponde alla frequenza dell’oscillazione sonora.
Per rappresentare le onde sonore occorre effettuare una semplificazione per poter
ridurre casi complessi (interferenze, increspature) a casi più semplici (il caso ideale è
quello di un'onda costante che si espande nello spazio libero). Il suono più semplice
può essere rappresentato utilizzando una sinusoide semplice in quanto può facilmente
rappresentare oscillazioni costanti nel tempo e nell’ampiezza.
L'asse orizzontale (delle ascisse) è l'asse del tempo (t), l'asse verticale (delle ordinate)
è l’asse delle ampiezze (A), dove andremo a leggere l'intensità delle oscillazioni.
Un’oscillazione sinusoidale è caratterizzata dal ripetersi ad intervalli regolari (periodi)
della sua forma o ciclo di oscillazione.
Silvio Relandini 8
Il suono acustico – capitolo 2
___________________________________________________________________________
Il ciclo di oscillazione dell’onda è misurato in Hertz (Hz), unità di misura della
frequenza f, che esprime il numero di cicli che avvengono nell’unità di tempo
(secondi).
1 Hz corrisponde a un moto in cui ha luogo un’oscillazione al secondo, mentre 10 Hz
corrisponde a un moto dove avvengono dieci oscillazioni al secondo. Il periodo T
invece è il tempo impiegato ad effettuare un’oscillazione: nel primo caso (1 Hz) il
periodo T vale 1 secondo, mentre nel secondo caso (10 Hz) vale un decimo di
secondo.
Da queste osservazioni si deduce anche che il periodo risulta essere l’inverso della
frequenza:
T=
1
f
Se invece del tempo consideriamo lo spazio, allora al posto del periodo si utilizza la
lunghezza d’onda λ definita come la distanza che esiste tra due picchi d’onda
consecutivi ed è misurata in metri.
Silvio Relandini 9
Il suono acustico – capitolo 2
___________________________________________________________________________
Il nostro sistema uditivo è in grando di produrre delle sensazioni sonore solamente per
un intervallo di frequenze compreso da 20 Hz fino a 20.000 Hz. Al disotto dei 20 Hz si
parla di infrasuoni, mentre al di sopra dei 20 kHz (k sta per kilo e vale 1000) abbiamo
gli ultrasuoni, l’intervallo 20 – 20 kHz determina la banda udibile. Questo intervallo
con l’avanzare degli anni tende a restringersi da entrambi i limiti.
Relazione tra frequenza e note musicali
Come sappiamo i musicisti individuano le varie altezze dei suoni non con valori delle
frequenze bensì con le note musicali. Che relazione esiste tra le note e le frequenze?
La frequenza usata come standard internazionale di riferimento, corrispondente al La
del corista indicato con la dizione anglosassone A4, è fissata a 440 Hz. In base a
questa convenzione, per calcolare la frequenza delle altre note si utilizza la seguente
formula:
f =2
N
12
⋅ f rif
dove:
frif = 440 Hz
N = n° di semitoni di distanza dalla nota di riferimento
Ad esempio, valutiamo qual è la frequenza del Si4:
2
12
f = 2 ⋅ 440 = 1,1125 ⋅ 440 = 493,3
Silvio Relandini 10
Il suono acustico – capitolo 2
___________________________________________________________________________
Nella tabella sono riportate le frequenze corrispondenti a tutte le note
Note
Do
Do#-Reb
Re
Re#-Mib
Mi
Fa
Fa#-Solb
Sol
Sol#-Lab
La
La#-Sib
Si
0
16,35
17,32
18,35
19,45
20,60
21,83
23,12
24,50
25,96
27,50
29,14
30,87
1
32,70
34,65
36,71
38,89
41,20
43,65
46,25
49,00
51,91
55,00
58,27
61,74
2
65,41
69,30
73,42
77,78
82,41
87,31
92,50
98,00
103,8
110,0
116,5
123,5
3
130,8
138,6
146,8
155,6
164,8
174,6
185,0
196,0
207,7
220,0
233,1
246,9
4
261,6
277,2
293,7
311,1
329,6
349,2
370,0
392,0
415,3
440,0
466,2
493,9
ottave
5
523,3
554,4
587,3
622,3
659,3
698,5
740,0
784,0
830,6
880,0
932,3
987,8
6
1047
1109
1175
1245
1319
1397
1480
1568
1661
1760
1865
1976
7
2093
2217
2349
2489
2637
2794
2960
3136
3322
3520
3729
3951
8
4186
4435
4699
4978
5274
5588
5920
6272
6645
7040
7459
7902
9
8372
8870
9397
9956
10548
11175
11840
12544
13290
14080
14917
15804
Il Timbro di un suono
Il Timbro è quella caratteristica del suono per la quale, a parità di frequenza, è
possibile distinguere due suoni prodotti da sorgenti diverse come ad es il suono di uno
strumento da quello di un altro (vedi un flauto e una chitarra). Il timbro dipende dal
contenuto spettrale del suono costituito dalla somma di componenti sinusoidali
desrivante dell’analisi di Fourier.
I suoni innanzitutto possono essere distinti in periodici e non periodici. Nei primi è
possibile distinguere un ciclo di oscillazione che si ripete nel tempo mentre nei secondi
(classificati generalmente come rumore) no.
Se un suono è periodico sarà possibile associare ad esso un’altezza stabilita e pertanto
avremo come percezione sonora un tono o una nota. Invece, nei suoni non periodici
questo non è possibile poiché il cervello non riesce a contare i cicli di oscillazione.
Nella musica entrambe le tipologie sono molto importanti in quanto i suoni periodici
sono utilizzati per creare la melodia e l’armonia mentre quelli non periodici sono
utilizzati principalmente per la ritmica.
Un suono periodico può essere semplice (puro), ovvero costituito da un’onda
sinusoidale (un’ampiezza e una frequenza), oppure complesso, costituito cioè da due
o più componenti sinusoidali che contribuiscono alla creazione di una forma d’onda
complessa. I suoni puri in natura sono molto rari e sono definiti come onda sonora la
cui pressione acustica istantanea è funzione sinusoidale del tempo.
Silvio Relandini 11
Il suono acustico – capitolo 2
___________________________________________________________________________
Relazione tra le componenti sinusoidali di un suono periodico complesso
Tra i suoni esistono le seguenti relazioni, che sono il frutto di millenni di studi (i primi
furono i cinesi, per ciò che ci riguarda Pitagora diede un grande contributo, ma
recentemente si è scoperto che anche l’uomo di Neanderthal costruiva flauti che
emettevano suoni i cui rapporti seguivano le stesse regole):
-OTTAVA, rapporto 2:1 in frequenza, ovvero preso un suono di frequenza F, il suono
all’ottava superiore ha una frequenza pari a 2F. Questo termine deriva dal fatto che
nella cultura occidentale, tra due suoni di cui il superiore ha una frequenza doppia
esistono otto note (do – re – mi – fa – sol – la – si – do).
-SESTA (maggiore), rapporto 5:3 in frequenza, ovvero preso un suono di frequenza F,
il suono ad una terza superiore ha una frequenza pari a 1,67F (do – re – mi – fa – sol
- la).
-QUINTA (perfetta), rapporto 3:2 in frequenza, ovvero preso un suono di frequenza F,
il suono ad una quinta superiore ha una frequenza pari a 1,5F. Anche in questo caso il
nome è legato alla cultura occidentale (do – re – mi – fa – sol).
Silvio Relandini 12
Il suono acustico – capitolo 2
___________________________________________________________________________
-QUARTA (perfetta), rapporto 4:3 in frequenza, ovvero preso un suono di frequenza F,
il suono ad una quarta superiore ha una frequenza pari a 1,33F (do – re – mi – fa).
-TERZA (maggiore), rapporto 5:4 in frequenza, ovvero preso un suono di frequenza F,
il suono ad una terza superiore ha una frequenza pari a 1,25F (do – re – mi).
La successione degli armonici è la seguente:
fondamentale:
F
1° armonico:
2F
ottava
2° armonico:
3F
un’ottava + una quinta
3° armonico:
4F
due ottave
4° armonico:
5F
due ottave + una terza maggiore
5° armonico:
6F
due ottave + una quinta
Silvio Relandini 13
Il suono acustico – capitolo 2
___________________________________________________________________________
Rappresentazione del timbro tramite lo spettro acustico
Per poter valutare il contenuto sonoro di un timbro si utilizza un grafico chiamato
spettro acustico, che ha sull’asse delle ordinate i valori dell’ampiezza mentre sull’asse
delle ascisse sono riportate le frequenza.
Nell’immagine seguente è riportato lo spettro acustico (grafico B) relativo ad un suono
puro sinusoidale
Nella figura successiva invece è mostrato lo spettro acustico di un suono complesso,
costituito dalla somma di più suoni sinusoidali.
Silvio Relandini 14
Il suono acustico – capitolo 2
___________________________________________________________________________
Vediamo
un
suono
complesso
così
come
potrebbe
apparire
utilizzando
un
oscilloscopio:
La componente sinusoidale di frequenza più bassa presente nello spettro acustico è
detta fondamentale mentre le altre componenti vengono indicate come parziali.
Queste ultime sono poi distinte in parziali armoniche se sono un multiplo intero della
fondamentale, la cui frequenza è f (ad es. 2f, 3f, 4f, 5f …) oppure in parziali non
armoniche negli altri casi (ad es. 2.1f, 3.7f … ).
Ad esempio:
1) se la frequenza della fondamentale è 100 Hz, gli armonici sono: primo 200 Hz (2f);
secondo 300 Hz (3f); terzo 400 Hz (4f); quarto 500 Hz (5f); ecc. ecc.
2) se la frequenza della fondamentale è 150 Hz, gli armonici: primo 300 Hz (2f);
secondo 450 Hz (3f); terzo 600 Hz (4f); quarto 750 Hz (5f); ecc. ecc.
Un suono periodico complesso pertanto può essere costituito dalla fondamentale e da
una serie numerosa di parziali armoniche e non armoniche.
Il periodo della fondamentale coincide anche con quello dell’onda risultante.
Nell’immagine successiva è mostrato uno spettro relativo ad un suono periodico
complesso.
Silvio Relandini 15
Il suono acustico – capitolo 2
___________________________________________________________________________
La fondamentale è espressa in colore blu, le parziali armoniche in colore nero, quelle
non armoniche in colore rosso.
Silvio Relandini 16