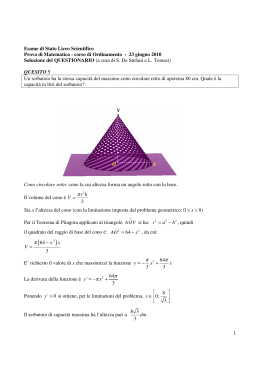
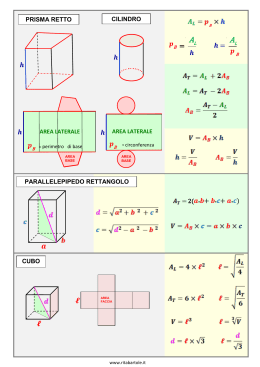
In una sfera di raggio r inscrivere il cono avente la superficie laterale massima. Soluzione 1 Posto BH x 2 BD DH BH x 0 , r con r 2 x2 si ha: CH DH r r 2 x 2 2 2 r r 2 x 2 x 2 r 2 r 2 x2 2r r 2 x2 x 2 r 2r 2 2r r 2 x2 . La funzione da rendere massima è: S (x) r 1 2 BH BD ; 2 Agli estremi x 0 e S (x) x 2 r 2 2 r r 2 x 2 x x r il cono degenera nel diametro avente superficie nulla. 2x 2r 2 r 2 x2 La derivata prima è: S I x 1 2 r 2 2 r r 2 x 2 x 2 2r 2 2r r 2 x 2 r x2 r 2 x2 2r 2 2r r 2 x 2 2r 2 2r r 2 x 2 2r 2 r 2 x 2 2r r 2 x2 r x 2 2 r 2 x2 2 2r 2r r x 2 2 r 2 r 2 x 2 2 r 3 3 rx 2 r x2 2 2 2 2 r 2 r r x r 2 x2 2r 2 2r r 2 x2 2 r 2 r 2 x 2 2 r 3 2 rx 2 r x 2 r 2 x2 2 2 2r 2r r x r 2 x2 2r 2 2r r 2 x 2 2 2 r 2 r 2 x 2 2 r 3 3 rx 2 r 2 x 2 2 r 2 2 r r 2 x 2 La derivata prima S I (x) 0 per: 2 r 2 r 2 x 2 2 r 3 3 rx 2 r 2 2 r 2 r 2 x 2 2 r 3 3 rx 2 0 ; 0; x 2 2 r 2 2 r r 2 x 2 2 2 r 2 r 2 x 2 3 rx 2 2 r 3 2 ; 4 r 6 4 r 4 x 2 9 r 2 x 4 4 r 6 12 r 4 x 2 0 ; x2 0 9r 2 x 2 8 r 4 0 Matematica x2 0 x2 8r 4 9r 2 4 r 4 r 2 x 2 9 r 2 x 4 4 r 6 12 r 4 x 2 ; 9r 2 x 4 8 r 4 x 2 0 ; x 2 9r 2 x 2 8 r 4 0 ; x 0 doppia x 2 2 r la soluzione negativa non è accettabile 3 www.mimmocorrado.it 1 Essendo: S (0) 0 2 r 2 2 r r 2 0 2 0 S ( ) r 2r 2 2r r 2 r 2 2 r 2 2 2 S 3 2 2 2 2 r r 2 r 2 2 r r 2 3 3 r 2 2 r 2r 2 2r 3 8 2 8 r 3 9 3 3 Il massimo assoluto è M 8 3 r2 9 2 2 8 r 2r 2 2r r 2 r 2 3 9 2 assunto nel punto x 2 2 r 3 r 2 2 8 2 r r 3 3 3 r2 Si può concludere quindi che il cono avente la superficie laterale massima ha il raggio di base uguale a x Matematica www.mimmocorrado.it 2 2 r. 3 2 Soluzione 2 x 0 , r Posto BH x con si ha: CH r 2 x2 2 BD DH BH DH r r 2 x 2 r r 2 x 2 x 2 r 2 r 2 x2 2r r 2 x2 x 2 r 2 2 r 2r 2 2r r 2 x2 x La funzione da rendere massima è: S (x) 1 2 BH BD ; 2 Agli estremi x 0 e S (x) x 2 r 2 2 r r 2 x 2 x r il cono degenera in un segmento (il diametro) avente superficie nulla. 2x 2r 2 r 2 x2 La derivata prima è: S I x 1 2 r 2 2 r r 2 x 2 x 2 2r 2 2r r 2 x 2 r x2 r 2 x2 2r 2 2r r 2 x 2 2r 2 2r r 2 x 2 2r 2 r 2 x 2 2r r 2 x2 r x 2 2 r 2 x2 2 2r 2r r x 2 2 2 2r 2r r x 2 r 2 r 2 x 2 2 r 3 3 rx 2 r x2 2r 2 2r r 2 x 2 r 2 x2 2r 2 2r r 2 x2 2 r 2 r 2 x 2 2 r 3 2 rx 2 r x 2 r 2 x2 r 2 x2 2r 2 2r r 2 x 2 2 2 r 2 r 2 x 2 2 r 3 3 rx 2 r 2 x 2 2 r 2 2 r r 2 x 2 La derivata prima S I (x) 0 per: 2 r 2 r 2 x 2 2 r 3 3 rx 2 r 2 2 2 2 2 2 r 2 r 2 x 2 3 rx 2 2 r 3 2 ; 2 2 x 9r x 8 r Matematica 4 0 ; 4 r 4 r 2 x 2 9 r 2 x 4 4 r 6 12 r 4 x 2 ; 4 r 6 4 r 4 x 2 9 r 2 x 4 4 r 6 12 r 4 x 2 0 ; 2 2 r 2 r 2 x 2 2 r 3 3 rx 2 0 ; 0; x 2 r 2 r r x 2 9r 2 x 4 8 r 4 x 2 0 ; x2 0 9r 2 x 2 8 r 4 0 x2 0 x2 8r 4 9r 2 www.mimmocorrado.it x 0 doppia x 2 2 r 3 3 S I x 0 ; 2r 2 2 2 r 2 r 2 x 2 2 r 3 3 rx 2 2 r 2 0; x 2 2 r 2 2 r r 2 x 2 3 2 r x 2 r 3 rx 0 (*) 2 r x2 0 2r 2 2r r 2 x 2 0 2 2 r 3 0 2 2 x r 3 r x r NO NO r x r (**) r SI ( x ) - + S ( x) Si può concludere quindi che il cono avente la superficie laterale massima ha il raggio di base uguale a x 2 2 r. 3 Calcoli La disequazione (*) 2 r 2 r 2 x 2 2 r 3 3 rx 2 0 ; r 2 x2 dividendo per 2 r 2 0 si ha: r 2 x2 r 3x2 0; 2r cioè: 3 2 x r 2r 3 2 x r 0 La soluzione di tale equazione è data dall’unione dei due sistemi: A 2 r r 2 x 2 0 3 2 x r 0 A 2r r 2 x 2 0 2 2 r x r 3 3 r x r 3 2 2r x r 0 B 2 r 2 x 2 3 x 2 r 2r Pertanto (**) 2 r 3 0 NO 2 r r 2 x 2 2 r 2 3 x 2 0 per x 2 La disequazione (# ) r 2 x 2 3 x 2 r ; 2r r 2 x2 2 2 2 r x r 3 3 0 x 0 9 2 x 2 0 4r 2 2 2 2 2 x r; x r 3 3 0x 2 r 3 2 r 3 2 2 r 3 r NO NO 2 2 r . 3 9 4 x r 2 3x2 ; 4r 2 2 2 r 3 0 x2 0 r NO 2 2 r; x r x 3 3 2 2 0 x 3 r (# ) 3 2 2r x r 0 B 2 r 2 x 2 3 x 2 r 2r 9 4 x 2x2 0 ; 4r 2 r NO NO 9 x2 2 x2 2 0 4r 0x 2 2 r 3 + La disequazione (**) 2r 2 2r r 2 x 2 0 ; Matematica essendo r 0 r 2 x 2 0 ; r x r . www.mimmocorrado.it 4
Scaricare