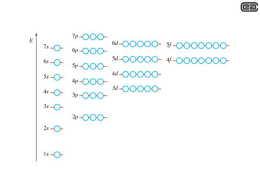
UNIVERSITÀ DEGLI STUDI DI PARMA
FACOLTÀ DI SCIENZE MATEMATICHE, FISICHE E NATURALI
CORSO DI LAUREA IN FISICA
Effetti isotopici nelle proprietà elettroniche
delle fulleriti superconduttive
Relatore:
Prof. Mauro Riccò
Correlatore: Prof. Paolo Santini
Candidato:
Fabio Gianferrari
anno accademico 2002-2003
This document was typeset in Adober Utopia and Computer Modern Roman
by the author using the LATEX2ε software.
The file in Portable Document Format was generated with pdfTEX version 13c.
c Copyright 2003 by Fabio Gianferrari. All Rights Reserved.
Author’s address
Fabio Gianferrari
Dipartimento di Fisica
Università degli Studi di Parma
Parco Area delle Scienze 7A, I-43100 Parma, Italy
E-mail: [email protected]
Riassunto
La molecola di C60 è la più stabile e simmetrica delle molecole appartenenti alla famiglia
dei fullereni, che costituiscono la terza forma allotropica del carbonio, dopo la grafite e il
diamante. Essi sono molecole originate da un piano di grafite che si richiude su se stesso,
producendo una superficie globulare composta da pentagoni ed esagoni.
Le fulleriti sono una famiglia a sè stante di composti organici, costituite da cristalli molecolari di C60 , nei quali vengono intercalati atomi di metalli alcalini che vanno ad occupare
siti interstiziali. Si è scoperto che le fulleriti del tipo A3 C60 (A=K, Na, Rb, Cs), che a temperatura ambiente sono metalli, a basse temperature (dell’ordine di 10-40 K) mostrano un
comportamento superconduttivo. Sebbene sia ormai chiaro che questo tipo di superconduttività è da attribuirsi ad un meccanismo d’accoppiamento tradizionale “elettrone−fonone”,
questi materiali hanno mostrato andamenti dei parametri caratteristici non conformi alle previsioni delle tradizionali teorie BCS e Migdal-Eliashberg. Esse risultano inadeguate al fine di
spiegare la superconduttività delle fulleriti dal momento che, in questi materiali, l’energia dei
fononi coinvolti (∼0.2 eV) risulta confrontabile con l’energia di Fermi (∼0.5 eV). Ciò crea una
situazione non trattabile nel quadro adiabatico in cui sono formulate le teorie tradizionali.
La fenomenologia dei superconduttori fullerenici sembra trovare una spiegazione più naturale
nei modelli di superconduttività nonadiabatici; in particolare in questa tesi si fa esplicito
riferimento ai lavori teorici di L. Pietronero et al.1
Questi modelli hanno previsto l’insorgere di cambiamenti nelle proprietà elettroniche delle
fulleriti anche nella fase normale, oltre che in quella superconduttiva. Uno dei principali test
di consistenza per la teoria nonadiabatica è senza dubbio la misura del possibile effetto
isotopico sulla suscettibilità di spin nella fase normale del conduttore. Tale effetto, previsto
dai modelli di superconduttività nonadiabatica sopra citati, non è contemplato nelle teorie
convenzionali BCS e Migdal-Eliashberg. La misura della suscettibilità di Pauli χp è stata
effettuata con un magnetometro SQUID su campioni di K3 C60 , con un’abbondanza naturale
di 13 C e arricchiti all’85%. Il valore di χp per i campioni arricchiti è risultato sistematicamente
inferiore a quello misurato nei campioni costituiti da un’abbondanza naturale di 13 C. Questo
conferma la presenza di un effetto isotopico, anche se tale effetto consiste in una diminuzione
della suscettibilità di Pauli diversamente da quanto ci si aspetterebbe in base alle previsioni
teoriche che indicano un lieve aumento di χp nei campioni arricchiti.
Il lavoro sperimentale è stato in parte dedicato anche ad una misura alternativa di χp
attraverso misure di NMR, in quanto la risposta magnetica degli elettroni di conduzione
(che determinano χp ) induce una polarizzazione magnetica nei nuclei di 13 C. In particolare
si è messo a punto l’apparato simulativo necessario per dedurre tale quantità dagli spettri
misurati.
1
Grimaldi, C., Pietronero, L., and Strässler, S. Nonadiabatic Superconductivity: Electron-Phonon
Interaction Beyond Migdal’s Theorem. Physical Review Letters 75, 6 (August 1995), 1158–1161.
Grimaldi, C., Pietronero, L., and Strässler, S. Nonadiabatic Superconductivity II: Generalized
Eliashberg equations beyond Migdal’s theorem. Physical Review B 52, 14 (October 1995), 10530–10546.
ii
Indice
Introduzione
1
1 Struttura e superconduttività dei composti del C60
1.1 Struttura molecolare del C60 . . . . . . . . . . . . . . . . . . . .
1.2 Struttura elettronica del solido . . . . . . . . . . . . . . . . . . .
1.3 Superconduttività . . . . . . . . . . . . . . . . . . . . . . . . . .
1.3.1 Parametri caratteristici dei materiali superconduttori . . .
1.3.2 Le fulleriti superconduttive A3 C60 . . . . . . . . . . . . .
1.3.2.1 Superconduttività non adiabatica . . . . . . . .
1.3.2.2 Suscettibilità di spin χ in regime nonadiabatico
2 Tecniche sperimentali
2.1 Magnetometria SQUID . . . . . . . . . . . . . . . .
2.1.1 Metodologia di misura . . . . . . . . . . . .
2.2 Fondamenti di risonanza magnetica nucleare NMR
2.2.1 Interpretazione semiclassica . . . . . . . . .
2.2.2 Interpretazione quantistica . . . . . . . . .
2.2.3 Sistemi macroscopici di spin . . . . . . . . .
2.3 Fenomeni di rilassamento . . . . . . . . . . . . . .
2.3.1 Rilassamento spin-spin . . . . . . . . . . . .
2.3.2 Rilassamento spin-reticolo . . . . . . . . . .
2.4 Interazioni di base in NMR dello stato solido . . .
2.4.1 Interazione Zeeman . . . . . . . . . . . . .
2.4.2 Interazione dipolare diretta . . . . . . . . .
2.4.3 Interazione dipolare indiretta (J-coupling) .
2.4.4 Interazione di chemical shift . . . . . . . . .
2.4.5 Interazione di Knight shift . . . . . . . . . .
2.5 Apparato sperimentale NMR . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
3 Misure e risultati
3.1 Misure di magnetizzazione . . . . . . . . . . . . . . . . . . . . .
3.2 Misure NMR . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.2.1 NMR su 13 C . . . . . . . . . . . . . . . . . . . . . . . .
3.2.2 Determinazione dei tempi di rilassamento spin-reticolo .
3.2.3 Rinormalizzazione in peso della suscettibilità . . . . . .
3.2.4 Analisi della forma di riga in funzione della temperatura
iii
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
3
3
5
7
8
9
13
17
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
21
21
22
25
27
28
29
31
31
33
35
36
36
40
41
42
44
.
.
.
.
.
.
49
49
54
56
59
61
62
4 Simulazioni della forma di riga NMR
4.1 Modello semplificato del sistema di spin . . . . . . . . . . . . . . . . . .
4.2 Formulazione teorica . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.2.1 Rappresentazione degli operatori di spin . . . . . . . . . . . . . .
4.2.2 Hamiltoniana del sistema di spin . . . . . . . . . . . . . . . . . .
4.2.3 Evoluzione temporale e acquisizione . . . . . . . . . . . . . . . .
4.3 Descrizione del programma . . . . . . . . . . . . . . . . . . . . . . . . .
4.3.1 GAMMA C++ library . . . . . . . . . . . . . . . . . . . . . . . .
4.3.2 Simulazione di esperimenti NMR . . . . . . . . . . . . . . . . . .
4.3.3 Struttura delle simulazioni in GAMMA . . . . . . . . . . . . . .
4.4 Simulazioni delle sole interazioni di shift . . . . . . . . . . . . . . . . . .
4.5 Simulazioni della sola interazione dipolare . . . . . . . . . . . . . . . . .
4.6 Simulazioni comprensive di interazione dipolare, chemical e Knight shift
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
65
65
66
67
68
70
71
71
72
74
77
77
79
Conclusioni
81
Bibliografia
83
iv
Elenco delle figure
1
2
3
4
5
6
7
8
9
Icosaedro troncato . . . . . . . . . . . . . .
Molecola di C60 . . . . . . . . . . . . . . . .
Livelli energetici del C60 . . . . . . . . . . .
Struttura fcc . . . . . . . . . . . . . . . . .
Dinamica reticolare in A3 C60 . . . . . . . .
Diagramma di fase . . . . . . . . . . . . . .
Potenziale elettrone−fonone nonadiabatico .
Suscettibilità di spin . . . . . . . . . . . . .
Coefficiente isotopico αχ . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
3
4
6
7
12
14
16
18
18
10
11
12
13
14
15
16
17
18
19
20
21
22
23
Schema di principio di uno SQUID . . . . . . . .
Struttura di un magnetometro SQUID . . . . . .
Schema di uno SQUID DC . . . . . . . . . . . .
Segnale SQUID . . . . . . . . . . . . . . . . . . .
Precessione . . . . . . . . . . . . . . . . . . . . .
Traiettoria classica di µ . . . . . . . . . . . . . .
Eco di Hahn . . . . . . . . . . . . . . . . . . . . .
Diagramma delle interazioni NMR . . . . . . . .
Livelli Zeeman di due spin 1/2 . . . . . . . . . .
Transizioni dipolari . . . . . . . . . . . . . . . . .
Pake doublet dipolare di due spin 1/2 . . . . . .
Interazione di J-coupling . . . . . . . . . . . . . .
Schema a blocchi dell’apparato NMR . . . . . . .
Schematizzazione del circuito di una sonda NMR
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
22
23
24
25
27
28
33
35
37
38
39
40
45
46
24
25
26
27
28
29
30
31
32
33
34
35
36
37
Curva di magnetizzazione di una generica fullerite superconduttiva . . . . .
Misura SQUID della magnetizzazione del K3 C60 . . . . . . . . . . . . . . .
Set di misure SQUID ripetute a diversi campi applicati . . . . . . . . . . .
Magnetizzazione in funzione del campo per il K3 C60 . . . . . . . . . . . . .
Laboratorio NMR . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Struttura interna di un magnete superconduttore. . . . . . . . . . . . . . . .
Spettro NMR di K3 C60 . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Spettri NMR di 13 C del C60 puro e del K3 C60 in campioni arricchiti . . . .
Spettri NMR di 13 C a temperatura ambiente . . . . . . . . . . . . . . . . .
Stima del tempo di rilassamento T1 nel K3 C60 . . . . . . . . . . . . . . . .
Stima del tempo di rilassamento T1 nel C60 puro arricchito . . . . . . . . .
Stima del tempo di rilassamento T1 del picco di C60 non reagito nel K3 C60
Analisi dei picchi per il campione UP . . . . . . . . . . . . . . . . . . . . . .
Spettri NMR di K3 C60 in funzione della temperatura . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
50
51
51
53
55
55
56
57
58
60
60
61
62
64
v
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
38
39
40
41
42
43
44
45
46
Modello del sistema di spin . . . . . . . . . . . . . . . . .
Tensore dipolare . . . . . . . . . . . . . . . . . . . . . . .
Struttura di GAMMA . . . . . . . . . . . . . . . . . . . .
Struttura di una singola acquisizione NMR . . . . . . . .
Classi che definiscono il sistema di spin in GAMMA. . . .
Simulazioni delle interazioni di shift . . . . . . . . . . . .
Circondario dipolare del carbonio rappresentativo . . . . .
Simulazione preliminare dello spettro da polvere dipolare
Confronto fra Spettro del K3 C60 a 30 K e riga simulata . .
vi
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
66
69
72
73
74
76
78
78
79
Introduzione
Questo lavoro di tesi rappresenta un contributo alla ricerca sui nuovi materiali a base di
carbonio, alcuni dei quali superconduttori, che si sono sviluppati in seguito alla scoperta dei
fullereni (H. W. Kroto et al. 1985), una famiglia a se stante di composti del carbonio il cui
più noto rappresentante è il C60 .
La molecola di C60 rappresenta il blocco elementare di cui sono costituite le strutture più
complesse di questi materiali; è il più stabile della famiglia dei fullereni, che costituiscono la
terza forma allotropica del carbonio, dopo la grafite e il diamante. La forma approssimativamente sferica della molecola lascia a disposizione nel cristallo una considerevole quantità
di spazio vuoto da poter occupare con altri costituenti che possono fungere da “spaziatori
molecolari”. Inoltre, grazie alle ampie proprietà redox del C60 , il solido molecolare può donare o ricevere elettroni: sfruttando questo fatto si possono preparare una grande varietà
di materiali con proprietà elettroniche differenti, pur con struttura cristallina simile. Questi materiali sono cristalli molecolari nei quali vengono intercalati atomi di metalli alcalini
che vanno ad occupare siti interstiziali con stechiometria variabile. Essi prendono il nome
di fulleriti e costituiscono una famiglia a se stante di composti del carbonio; alcuni sono
isolanti mentre altri conduttori, dal momento che il C60 ha orbitali π insaturi che allo stato
solido formano bande elettroniche, quindi sistemi metallici, se vi sono elettroni disponibili
ad occuparle. In particolare questo fatto si verifica nei composti con stechiometria A3 C60
(A=K, Na, Rb, Cs): si è scoperto che questi composti mostrano un comportamento metallico a temperature ambiente, mentre a basse temperature (dell’ordine di 10-40 K) diventano
superconduttori. Questi materiali hanno mostrato caratteristiche superconduttive particolari, con comportamenti dei parametri caratteristici non conformi alle previsioni della teoria
BCS (Bardeen-Cooper-Schrieffer), il primo modello teorico ab initio efficace nello spiegare il
meccanismo superconduttivo di buona parte dei superconduttori scoperti.
Sebbene sia ormai chiaro che la superconduttività delle fulleriti è basata su meccanismi
“tradizionali”, cioè accoppiamento elettrone−fonone, l’energia dei fononi coinvolti (∼0.2 eV)
risulta confrontabile con l’energia di Fermi (∼0.5 eV). Questo crea una situazione non trattabile sulla base delle classiche teorie BCS/Migdal-Eliashberg, originariamente formulate in un
quadro adiabatico. La teoria di Migdal-Eliashberg è una semplice estensione di quella BCS al
1
2
caso in cui le vibrazioni reticolari determinino un’interazione attrattiva efficace fra elettroni
moderatamente intensa, non debole come nel modello originale BCS, con conseguente forte
accoppiamento degli elettroni stessi. Tuttavia l’ipotesi di adiabaticità è comune ad entrambe queste teorie: esse partono dall’idea di poter separare la dinamica elettronica da quella
reticolare a causa delle diverse scale di energia e quantità di moto. In altri termini assumono che l’interazione elettrone−fonone, termine principale della hamiltoniana di un sistema
superconduttivo, sia adiabatica. Recenti estensioni di queste teorie al caso non adiabatico
hanno previsto effetti isotopici nelle proprietà elettroniche delle fulleriti anche nella fase normale, oltre che in quella superconduttiva. Ad esempio viene indicato un effetto isotopico sulla
suscettibilità di Pauli in fase normale: quest’ultima, a causa dei nuovi canali d’interazione
nonadiabatici, assumerebbe una dipendenza dalla massa isotopica del carbonio.
Funzioni di risposta quali la suscettività di spin sono investigabili, oltre che con le tradizionali tecniche magnetometriche, anche con la Risonanza Magnetica Nucleare attraverso la
misura del Knight shift. Quest’ultimo non è altro che un effetto di polarizzazione magnetica
dei nuclei da parte degli elettroni di conduzione. Il Knight shift è, in generale, anisotropo
e, traendo la sua origine dalla risposta magnetica degli elettroni metallici, è intrinsecamente
correlato alla suscettibilità di spin del materiale. Nel caso delle fulleriti, l’interazione iperfine
degli elettroni della banda di conduzione (t1u ) con il nucleo di carbonio è di carattere tensoriale, quindi il Knight shift può essere misurato solo attraverso una accurata analisi della
forma di riga.
In questo lavoro di tesi è stata effettuata una misura di suscettibilità sia con metodi tradizionali, sia utilizzando l’NMR del 13 C per studiare la presenza di possibili effetti isotopici sulla
suscettibilità di spin nella fase normale del conduttore. A tale scopo sono state confrontate
fulleriti composte da una abbondanza isotopica naturale di
13 C
con le stesse, isotopicamente
arricchite all’85%. È stato analizzato in particolare il K3 C60 come composto rappresentativo
dei superconduttori fullerenici.
Capitolo 1
Struttura e superconduttività dei
composti del C60
1.1
Struttura molecolare del C60
La molecola di C60 fu scoperta nel 1985 da H. W. Kroto durante ricerche sulle lunghe catene
di atomi di carbonio nello spazio interstellare; è la molecola più simmetrica e stabile della
famiglia dei fullereni (dei quali fanno parte anche le molecole di C70 , C84 ,..., fino a C100 e
altre ancora, alcune delle quali instabili). I 60 atomi di carbonio sono disposti in modo da
formare 12 pentagoni e 20 esagoni: è la struttura di un icosaedro (poligono regolare a 20
facce) troncato da piani ortogonali alla congiungente dei vertici col centro, esattamente la
struttura delle cuciture di un pallone da calcio.
Figura 1: Icosaedro troncato
Il C60 ha il più alto grado di simmetria puntuale di tutte le strutture conosciute, perchè
appartiene al gruppo puntuale icosaedrico (Ih ), il quale comprende ben 120 operazioni di
simmetria.
Cosı̀ come nel benzene e nella grafite, di gran lunga anche nel C60 gli orbitali atomici di
interesse sono principalmente gli orbitali pz dove l’asse z risulta fisso nel caso di molecole
piane, mentre nel C60 è in direzione radiale. È noto che si può immaginare il C60 come un
piano di grafite racchiuso su se stesso con il risultato che la differenza di curvatura fra le due
3
4
1. Struttura e superconduttività dei composti del C60
strutture porta ad orbitali molecolari derivati da un diverso set di orbitali atomici: per la
grafite sono coinvolti gli orbitali pz e sp2 , mentre nel C60 si riscontra una diversa ibridazione
sempre fra s e pz (∼9% di s in pz ). Ogni atomo di carbonio partecipa a 3 legami, due dei quali
costituiscono un lato condiviso fra un pentagono e un esagono (legami “5-6” ∼1.45 Å) mentre
il terzo rappresenta il lato comune fra due esagoni (legame “6-6” ∼1.40 Å). Quest’ultimo è
considerato formalmente un doppio legame; in realtà la differenza di lunghezza fra questo
legame e quello precedente è piccola in confronto a quella che ci si aspetterebbe in base alle
lunghezze di legame C-C dei composti noti (legame singolo del diamante ∼1.54 Å, doppio
dell’etilene ∼1.34 Å, triplo degli alchini ∼1.20 Å). Inoltre i legami del C60 sono più simili ai
legami del benzene ∼1.39 Å o della grafite ∼1.41 Å: è ragionevole allora immaginare che il
doppio legame sia delocalizzato proprio come avviene nella grafite.
Figura 2: Molecola di C60 e rappresentazione dei legami a cui partecipa ogni atomo: tutti
i carboni sono equivalenti dal punto di vista del circondario elettronico locale. Gli angoli di
legame interni agli esagoni sono sempre di ∼ 120◦ , come nella grafite, mentre il terzo angolo
(interno alla faccia pentagonale) è di 108◦ , data la sensibile deviazione dalla geometria piana. Il
raggio molecolare è 3.55 Å, ma, nel caso si considerino anche i gusci elettronici, arriva a 5.02 Å.
Tutti questi legami coinvolgono complessivamente 180 elettroni in orbitali molecolari σbonding sp2 (anche se la deviazione dalla geometria planare ne altera lievemente il carattere). I rimanenti 60 elettroni sono distribuiti in orbitali di tipo π che traggono origine dagli
orbitali pz degli atomi di carbonio orientati in direzione radiale. Questi orbitali concorrono a
formare un insieme di orbitali molecolari delocalizzati, la cui formazione permette un guadagno energetico addizionale all’intera struttura, e contribuisce a determinarne la stabilità. La
struttura elettronica responsabile dei fenomeni di superconduttività delle fulleriti è legata a
questi orbitali π.
5
1.2. Struttura elettronica del solido
1.2
Struttura elettronica del solido
La struttura del C60 puro, come anche quella delle fulleriti superconduttive, è cubica a facce
centrate (tabella 1). Dato che il fullerene solido e le fulleriti sono solidi molecolari, la comprensione delle caratteristiche della singola molecola è un punto di partenza fondamentale
per la comprensione delle proprietà elettroniche di questi composti. Si è evidenziato che il
ruolo delle vibrazioni degli atomi alcalini intercalati non è molto rilevante per l’interazione
elettrone−fonone, infatti non è stata trovata, ad esempio, alcuna dipendenza della temperatura di transizione superconduttiva Tc , dalla massa isotopica degli ioni alcalini; questo effetto
isotopico su Tc , al contrario, sarebbe certamente presente se le vibrazioni in questione fossero
determinanti per l’insorgere della superconduttività.
Ciò suggerisce che, alla base del meccanismo responsabile della superconduttività nelle fulleriti, ci siano le caratteristiche molecolari del C60 ed in particolare degli orbitali molecolari più
direttamente interessati al trasferimento di elettroni dal metallo alcalino al fullerene (quindi
della banda da loro derivata), oltre che le caratteristiche delle vibrazioni intra-molecolari.
La debolezza dei legami fra le molecole nel solido fa ritenere che molte delle proprietà degli
orbitali molecolari del C60 si possano trasferire, con lievi variazioni, alla banda in questione:
la struttura elettronica dei composti Ax C60 si può infatti giustificare sulla base dei calcoli
Extended Hückel [22] a partire dagli autostati energetici della molecola isolata di C60 .
I livelli energetici degli orbitali molecolari π sono mostrati in figura 3. Questi calcoli indicano anche che la densità degli stati della banda derivante dall’orbitale t1u (LUMO) è quasi
costante al variare del suo riempimento, il che è una conferma della predominanza delle caratteristiche molecolari del C60 nel solido. In realtà la debolezza di questi legami non porta
alla creazione di bande nel senso proprio del termine.
stechiometria
proprietà elettroniche
struttura
A1 C60
isolante
A3 C60
metallico e super-c.
Tc compresa fra 10 e 40 K
non metallico
piccola gap
isolante
struttura
polimerica
f cc
A4 C60
A6 C60
bct
bcc
Tabella 1: Caratteristiche delle principali fulleriti. A seconda della stechiometria degli alcalini
si riscontrano strutture e proprietà elettroniche completamente diverse, molte delle quali interpretabili in base alla “ banda di conduzione” formata da LUMO: ad esempio è evidente che le
fulleriti di tipo A6 C60 , avendo tale banda completamente piena, devono essere isolanti.
6
1. Struttura e superconduttività dei composti del C60
Le relazioni di dispersione del momento cristallino ~k, rappresentate in figura 3, sono calcolate
in base alle simmetrie del gruppo spaziale F m3̄m; dal momento che, a temperatura ambiente,
i fullereni ruotano in modo caotico, la posizione del singolo nucleo di
13 C
risulta fissa solo a
bassa temperatura, quando tutte le rotazioni del C60 sono inibite. Inoltre, anche in questo
caso, il disordine orientazionale dei fullereni nella struttura f cc del solido, rompe l’invarianza
traslazionale del sistema; infatti, nonostante il suo altissimo grado di simmetria (gruppo Ih ),
la struttura del C60 non è compatibile con le simmetrie puntuali del reticolo f cc; da questo
nasce il disordine orientazionale intrinseco del solido (disordine meroedrico). Abbiamo quindi
a che fare con un cristallo particolare, in cui l’ordine traslazionale esiste solo per il baricentro
delle molecole di C60 , non per i singoli atomi di carbonio. La dinamica rotazionale del C60
è complessa; a temperatura ambiente, le rotazioni sono assolutamente caoticche, solo sotto
una certa temperatura si “assestano” su alcune direzioni privilegiate. Comunque, anche in
questo caso, la molecola di C60 non diventa un rotatore fisso attorno ad un certo asse: compie
continuamente dei “salti” fra i vari assi permessi, senza rimanere mai lungo un certo asse per
tempi “macroscopici”. Questa transizione di fase orientazionale si verifica a 250 K; scendendo
ancora in temperatura, i moti rotazionali dei fullereni vengono completamente congelati: questo nel C60 puro avviene a 90 K. Nella regione di temperatura intermedia gli assi di rotazione
sembrano orientarsi lungo le quattro direzioni equivalenti (1,1,1) [34].
Figura 3: Livelli energetici del C60 . A sinistra sono rappresentati i livelli energetici molecolari
derivati dai 60 orbitali pz con corrispondenti degenerazioni e riempimento. Sono di interesse
principalmente HOMO (highest occupied molecular orbital) che ha simmetria hu , e LUMO
(lowest unoccupied molecular orbital), con simmetria t1u . A destra sono mostrate la struttura
a bande e la densità degli stati del K3 C60 : si vede che il drogaggio con un metallo alcalino ha
portato al parziale riempimento della stretta banda derivata dal LUMO (∼0.5 eV).
1.3. Superconduttività
7
Figura 4: Struttura f cc del K3 C60 . Sono rappresentati in blu gli atomi alcalini che occupano i
siti tetraedrici, mentre in rosso quelli che occupano siti ottaedrici.
Essenzialmente ciò che si vede a queste temperature è la manifestazione del disordine
meroedrico caratteristico del C60 in un reticolo f cc il cui gruppo spaziale F m3̄m, come
accennato prima, non è compatibile con il gruppo icosaedrico Ih .
L’esistenza di un simile moto lungo assi privilegiati è stata confermata anche nel Rb3 C60 e
K3 C60 da Yoshinari et al. [34, 35]: in quest’ultimo la transizione alla fase ordinata avviene
a 230 K in modo analogo a quanto visto nel C60 puro. È importante ricordare il risultato
delle precedenti analisi NMR sulle transizioni di fase orientazionali: il disordine meroedrico si
realizza nella presenza di due possibili orientazioni per ciascun fullerene, una ruotata di 90◦
rispetto all’altra; le molecole occuperanno casualmente una delle due e il tutto si schematizza
nella presenza di 3 siti reticolari di carbonio non equivalenti dal punto di vista cristallografico,
per i quali quindi la densità di carica (quella delocalizzata originata dalla shell π) può variare.
1.3
Superconduttività
È noto che la superconduttività è un fenomeno per cui alcune sostanze, non necessariamente
con caratteristiche metalliche, al di sotto di una certa temperature critica Tc , transiscono
8
1. Struttura e superconduttività dei composti del C60
ad uno stato caratterizzato, oltre che da resistenza nulla, anche da particolari proprietà
magnetiche: essi presentano l’effetto Meissner, ossia l’espulsione del campo magnetico esterno.
In altri termini, per campi non troppo elevati la magnetizzazione di un superconduttore
non dipende dalla storia termica del materiale, cosa che invece avviene per i conduttori
normali: in un superconduttore, il raffreddamento sotto Tc con o senza campo esterno produce
sempre il medesimo stato contraddistinto da una suscettività χ = M/Hext = −1. Questo è
vero rigorosamente solo per bassi campi: campi troppo elevati finiscono per distruggere la
superconduttività, ma questo avviene in modi diversi a seconda del tipo di superconduttore
considerato. I superconduttori, infatti, si dividono in due tipi:
• Tipo I. Il campo esterno è completamente espulso fino ad un valore critico Hc1 , ma al
di sopra di esso la superconduttività csompare del tutto.
• Tipo II. Il flusso è totalmente espulso solo per Hext < Hc1 , mentre per Hc1 < Hext < Hc2
si verifica una situazione intermedia in cui il campo penetra parzialmente generando
tubi di flusso magnetico (flussoni ) all’interno dei quali il materiale è allo stato normale.
Per un ulteriore breve chiarimento sull’origine di questi due distinti comportamenti, è utile
introdurre alcuni fondamentali parametri caratteristici.
1.3.1
Parametri caratteristici dei materiali superconduttori
Lunghezza di penetrazione
Anche se all’interno del materiale H = 0, deve esistere in superficie una zona di transizione in
cui il campo varia da Hext a zero; è proprio in questa zona che sono presenti le supercorrenti
che schermano il campo esterno (schermo diamagnetico permanente), correnti che, in un
conduttore normale, persistono solo fin quando Hext varia, poi non si conservano ma vengono
dissipate dalla normale resistività del materiale.
Lo spessore caratteristico di questa regione è detto lunghezza di penetrazione, λp .
Gap di energia
La transizione di fase superconduttiva si può pensare, nello spazio reciproco, come una condensazione degli stati elettronici attorno ad EF in uno stato comune con funzione d’onda
simmetrica. Questo nuovo stato fondamentale, costituito da bosoni a spin 0 detti coppie di
Cooper, è la evidente manifestazione della inapplicabilità del modello a elettroni indipendenti. Gli elettroni “normali” non accoppiati sono separati da un gap di energia dallo stato
fondamentale BCS: essi costituiscino il primo stato eccitato del sistema. È proprio questo
gap di energia che conferisce rigidità allo stato superconduttivo rendendolo stabile anche dal
punto di vista macroscopico. Si viene quindi a formare un gap attorno al livello di Fermi di
ampiezza 2∆, il quale indica l’energia necessaria per rompere (nella visione BCS) una coppia
di Cooper (dell’ordine di 1−10 meV).
1.3. Superconduttività
9
Lunghezza di coerenza
Si definisce ξ la lunghezza spaziale entro cui il parametro ∆ può variare, per esempio in
presenza di un campo magnetico non omogeneo, quindi vicino ad una zona di confine fra fase
superconduttiva e fase normale in un superconduttore di tipo II. In generale essa indica anche
la variazione spaziale caratteristica della funzione d’onda Ψ associata ai portatori; nel caso
particolare di un superconduttore di secondo tipo, rappresenta il raggio della zona interna ad
un flussone in cui la superconduttività è completamente distrutta.
Rapporto di Ginzburg-Landau
È il rapporto fra le due lunghezze caratteristiche λp e ξ,
κ=
λp
ξ
(1)
la sua importanza è legata al calcolo dell’energia libera dello stato superconduttore:
√
• κ > 1/ 2 =⇒ è conveniente la penetrazione del campo con flussoni, quindi il superconduttore risulta essere di tipo II.
√
• κ < 1/ 2 =⇒ la formazione di flussoni non è più una condizione di minimo dell’energia
libera, quindi si ha un superconduttore di tipo I.
1.3.2
Le fulleriti superconduttive A3 C60
I composti con stechiometria A3 C60 sono superconduttori del secondo tipo, con elevati campi critici superiori Hc2 (dell’ordine di 50 T) e bassi valori dei campi critici inferiori Hc1
(10−100 Gauss); quindi dal parametro di Ginzburg-Landau si deduce che hanno grandi lunghezze di penetrazione (∼200 nm) e lunghezze di coerenza relativamente piccole (∼1 nm). La
temperatura di transizione in alcuni casi può essere maggiore di 30 K (tabella 2).
Il meccanismo superconduttivo sembra essere un convenzionale accoppiamento elettronefonone, secondo il modello BCS esteso al caso di forte accoppiamento (teoria di MigdalEliashberg). L’ipotesi adiabatica è comunque sempre il punto di partenza della visione classica
della superconduttività. Nel caso di debole accoppiamento (la situazione di superconduttori
BCS come Al, Sn, KC8 , ecc.), le energie con cui si accoppiano gli elettroni nelle coppie di
Cooper sono basse perchè le vibrazioni reticolari sono solo una piccola perturbazione della
dinamica elettronica, quindi il potenziale efficace attrattivo che tiene legate le coppie è debole. Questo si formalizza nel fatto che la costante d’accoppiamento dell’interazione soddisfa
la condizione λ 1 (weak-coupling). Questo avviene perchè fondamentalmente le dinamiche reticolari e quelle elettroniche avvengono su due scale d’energia molto diverse (ipotesi
adiabatica). Questa ipotesi non viene necessariamente a mancare quando la condizione di
weak-coupling non è più soddisfatta; è necessaria solo una generalizzazione del formalismo
BCS che porta alla teoria di Migdal-Eliashberg.
10
1. Struttura e superconduttività dei composti del C60
Composto
Costante reticolare (Å)
Tc (K)
Na2 RbC60
Na2 CsC60
K3 C60
K2 RbC60
K2 CsC60
KRb2 C60
Rb3 C60
(NH3 )4 Na2 CsC60
Rb2 CsC60
14.028
14.133
14.253
14.299
14.292
14.364
14.436
14.473
14.493
2.5
11
19.2
21.8
24
26
29.4
29.6
31.3
Tabella 2: composti superconduttori
La costante λ, determina la forza dell’accoppiamento ed è proporzionale alla densità degli stati al livello di Fermi N (EF ) e all’elemento di matrice del potenziale attrattivo V che accoppia
gli elettroni tramite i fononi ωp . Nel limite di weak-coupling si ha:
1
− λ−µ
∗
k Tc = 1.6 ~ ωp e
,
(2)
dove µ∗ è lo pseudopotenziale coulombiano rinormalizzato: è necessario per tenere in considerazione il fatto che nei materiali reali Tc è abbassata dalla repulsione coulombiana. µ∗ è
dato da:
µ∗ =
µ
,
1 + µ ln ωEp
(3)
dove µ è lo pseudopotenziale coulombiano semplice. L’espressione di Tc si estende naturalmente al caso di forte accoppiamento secondo Eliashberg e McMillan. Un’espressione di Tc
particolarmente utile, sviluppata da quest’ultimo per λ 1.5, è
~ hωp i
k Tc =
e
1.2
−1.04(1+λ)
λ−µ∗ −0.62λµ∗
,
(4)
dove hωp i è una media logaritmica delle frequenze fononiche.
Questo tipo di approccio è stato in grado di descrivere con successo la fenomenologia di un
buon numero di composti metallici come Al (weak-coupling), Pb (strong-coupling). Tuttavia
le fulleriti drogate con metalli alcalini sono molto diverse dai convenzionali metalli: come
abbiamo detto questi materiali hanno bande di conduzione molto strette, in quanto solidi
molecolari, quindi le dinamiche elettroniche del cristallo sono di bassa energia; inoltre, essendo
il fullerene una molecola formata da legami covalenti, le vibrazioni intra-molecolari sono
molto più energetiche dei moti intra-molecolari caratteristici del reticolo f cc che formato
da legami deboli. Questa combinazione di fattori fa sı̀ che le scale d’energia elettroniche e
1.3. Superconduttività
11
fononiche intra-molecolari siano confrontabili e ciò fa inevitabilmente venir meno l’ipotesi
adiabatica. Tuttavia, l’interazione elettrone−fonone rappresenta ancora il punto di partenza
fondamentale per la comprensione del meccanismo superconduttivo. Inizialmente i modelli
teorici si sono focalizzati su 3 possibili meccanismi:
• accoppiamento mediato da modi intra-molecolari ad alta frequenza,
• accoppiamento mediato da una combinazione di modi intra-molecolari ad alta frequenza
e modi intercluster a bassa frequenza,
• accoppiamento con modi ottici di oscillazione fra C60 e ioni alcalini.
Nel primo caso i parametri dell’accoppiamento sono stati calcolati a partire dalle proprietà
della molecola di C60 ed è stata calcolata Tc con l’equazione (4). L’approssimazione ai soli
modi intra-molecolari si basa sul fatto che l’accoppiamento elettrone−fonone è proporzionale
all’ampiezza dello splitting degli stati molecolari del C60 (∼10 eV) che è molto maggiore
della larghezza della banda di conduzione t1u (∼0.5 eV), quindi le vibrazioni intra-molecolari
devono essere dominanti. In questo contesto si ricava
X g2
5
m
λ = N (EF )
,
2
6
M
ω
m
m
(5)
dove la somma è su m, vibrazioni intra-molecolari, e gm è l’m-esimo potenziale di deformazione intra-molecolare. Con calcoli semi-empirici si è visto anche che solo due modi tangenziali
Hg di frequenze 1428 e 1575 cm−1 si accoppiano fortemente con gli elettroni [16]. Un lavoro
successivo di Schluter et al. [29] ha portato a conclusioni sostanzialmente simili, con l’unica
differenza che nel calcolo della matrice d’accoppiamento, in questo secondo caso, risultano
essere significativi anche i termini dei modi intra-molecolari radiali Ag , a bassa frequenza.
Riassumendo, possiamo dire che per le fulleriti superconduttive si verifica la situazione unica
in cui la costante λ = N (EF )V si può fattorizzare in un primo termine N (EF ) determinato
dalla banda t1u , e in un termine intra-molecolare V che rappresenta i modi fononici interni
al fullerene.
Il modello di strong-coupling in cui l’interazione è mediata sia da fononi intra-molecolari,
che da quelli inter-molecolari a frequenza molto bassa, è stato proposto più recentemente da
Mazin et al. [20]. In questo caso la costante d’accoppiamento risulta fattorizzabile in due
termini, uno per le alte frequenze (λhf ∼ 2.7) e l’altro per le basse (λlf ∼ 0.5); a sua volta
λhf si fattorizzerà ancora in V e N (EF ).
Più che scendere nei dettagli dei vari modelli fononici proposti, i cui risultati sono sostanzialmente simili, è importante domandarsi fino a che punto l’applicabilità di questi approcci
sia lecita. Come affermato in precedenza l’energia di Fermi (EF ∼2000 cm−1 ) è confrontabile
con l’energia dei fononi intra-molecolari (ωp ∼1500 cm−1 ) responsabili dell’accoppiamento.
12
1. Struttura e superconduttività dei composti del C60
Figura 5: Rappresentazione schematica dei vari fononi nei composti del tipo A3 C60 : (a) librazioni; (b) fononi ottici C60 -C60 ; (d) ed (e) modi intra-molecolari Hg . La figura mette in evidenza
come Hg (7) sia più di carattere tangenziale, mentre Hg (1) sia prevalentemente radiale.
Energia (cm−1 )
Modi
Hg (8)
Hg (7)
Hg (6)
Hg (5)
Hg (4)
Hg (3)
Hg (2)
Hg (1)
Ag (2)
Ag (1)
Varmaa
1721
1596
1406
1260
924
711
447
263
Jishib
1575
1401
1217
1102
788
708
439
296
1468
492
Antropovc
1462
1387
1290
1091
785
753
454
281
1463
458
Quongd
1576
1443
1244
1093
767
727
439
258
1499
478
Faulhabere
1567
1425
1200
1067
750
640
421
249
1493
459
Expt.f
1575
1428
1250
1099
774
710
437
273
1470
496
Tabella 3: a Varma et al. 1991; b Jishi et al., 1992; c Antropov, Gunnarsson, and Liechtenstein,
1993; d Quong et al., 1993; e Faulhaber et al., 1993; f Bethune et al., 1991.
13
1.3. Superconduttività
Questo porta al breakdown dell’ipotesi adiabatica e alla conseguente inadeguatezza della
teoria di Migdal-Eliashberg. Un approccio differente, ad esempio, potrebbe essere quello
dei modelli di superconduttività puramente elettronici che cercano di spiegare il comportamento delle fulleriti con considerazioni sugli effetti di correlazione elettronica in questi
materiali [5, 11, 33]. Questi sono motivati parzialmente dal fatto che, essendo la banda di
conduzione del C60 stretta, la fisica del sistema può essere guidata ancora da interazioni
elettrone−elettrone, cioè interazioni fra singole particelle. Sono stati sviluppati vari modelli
per giustificare l’esistenza di coppie per mezzo di interazioni puramente elettroniche; è chiaro
che il principale problema di questo approccio è ottenere un’interazione efficace attrattiva fra
i due elettroni, nonostante la loro diretta repulsione coulombiana.
1.3.2.1
Superconduttività non adiabatica: interazione elettrone−fonone oltre il
teorema di Migdal
L’estensione del meccanismo elettrone−fonone in condizioni non adiabatiche sembrerebbe
essere l’evoluzione più naturale dei modelli teorici di superconduttività per le fulleriti; infatti in questi materiali l’idea BCS di accoppiamento fononico è sicuramente irrinunciabile,
nonostante il comportamento non BCS dei parametri caratteristici, come l’effetto isotopico
su Tc e l’ambigua valutazione di µ∗ . Un modello puramente elettronico sembrerebbe, molto
probabilmente, una spiegazione un po’ forzata del meccanismo superconduttivo: le fulleriti
si interpretano sempre tramite i classici parametri BCS; la costante d’accoppiamento non
è nemmeno cosı̀ alta da far pensare all’evoluzione nel regime polaronico [2], caratterizzato
da correlazioni elettroni−reticolo molto intense. La loro particolarità consiste proprio nella
difficoltà di calcolo dei parametri stessi che non vengono stimati correttamente dalla teoria di
Migdal-Eliashberg (M-E). In termini di λ e del parametro di adiabaticità hωp i/EF , la teoria
M-E non si applica se hωp i/EF non è trascurabile, anche se λ ∼ 1.
Ci troviamo in una condizione in cui i portatori di carica interagiscono debolmente con i
fononi, ma in modo non adiabatico: in questo regime si parla di fermioni non adiabatici [12]
per sottolineare la differenza col regime M-E e il limite polaronico. Il breakdown del teorema di Migdal, che asserisce la validità dell’ipotesi adiabatica fin tanto che hωp i EF [30],
è stato oggetto di molti articoli; in particolare in questo lavoro si fa riferimento ai modelli
di superconduttività non adiabatica di Pietronero, Cappelluti, Grimaldi, Strässler, Ummarino [8, 7, 13, 10].
Prima di tutto essi hanno stabilito che i dati sperimentali, nel caso del Rb3 C60 , sono incompatibili con le equazioni fondamentali M-E, essendo Tc = 36 K, 2∆ = 10.4 meV, α = 0.21.
L’equazione (4) assieme alle seguenti equazioni M-E:
1
α=
2
(1 + λ)(1 + 0.62λ)µ∗2
[λ − µ∗ (1 + 0.62λ)]2
,
(6)
14
1. Struttura e superconduttività dei composti del C60
Figura 6: Diagramma di fase delle fulleriti nel piano λ−hωp i/EF . La teoria di Migdal-Eliashberg
(M-E) è applicabile solo per quei materiali che si trovano sull’asse delle ascisse, per i quali
hωp i/EF ∼ 0. Le fulleriti invece si trovano in una regione di piano in cui il parametro di
adiabaticità è sensibilmente diverso da 0, per quanto λ sia bassa.
Per valori di λ troppo alti, l’accoppiamento col reticolo è cosı̀ forte da non poter più trattare
il sistema nei termini delle solite particelle; i modi normali vengono completamente stravolti e i
nuovi stati di particella che si formano sono detti polaroni: il sistema evolve secondo la dinamica
di queste particelle che si possono immaginare come elettroni vestiti dalle deformazioni reticolari
che li seguono. L’influenza reciproca elettroni−reticolo è cosı̀ forte, che entrambi perdono le
loro caratteristiche originarie.
dove α è l’esponente caratteristico dell’effetto isotopico su Tc ,
"
#
hωp i
Tc 2
η = 3.53 1 + 1.25
ln
,
hωp i
2Tc
(7)
dove η = 2∆/Tc (formula di Allen-Dynes), costituisce un sistema di tre equazioni in tre
incognite. Dunque è possibile ottenere una soluzione unica per i parametri caratteristici
λ = 3.9, µ∗ = 0.43, ωp = 210 K. Questi valori, confermati anche da una soluzione numerica
delle equazioni M-E, non sono soddisfacenti per i seguenti motivi:
- valore troppo alto di λ assolutamente irrealistico.
- valore troppo basso della frequenza.
- µ∗ è troppo elevato.
Le previsioni della teoria di Migdal-Eliashberg sono scorrette anche per altri parametri, come
ad esempio la variazione del calore specifico ∆Cv e il campo critico Hc del Rb3 C60 . Utilizzando
1.3. Superconduttività
15
il precedente valore di hωp i e il valore misurato di ∆Cv /Tc = 75 mJ/mol K2 , la costante di
Sommerfeld risulta γ ∼ 32 mJ/mol K2 . Questo valore si può utilizzare nell’equazione seguente
per il calcolo della quantità adimensionale R = γTc2 /Hc2 ,
"
#
hωp i
γTc2
Tc 2
= 0.168 1 − 12.2
ln
.
Hc2
hωp i
3Tc
(8)
Dal momento che il valore sperimentale del campo critico è Hc = 0.44 T, il primo membro
dell’equazione (8) risulta R ∼ 0.032 che è chiaramente inconsistente col valore del secondo
membro R ∼ 0.145 calcolato in base a hωp i.
Riassumendo, risulta evidente che, in base ai dati sperimentali, la convenzionale teoria
di Migdal-Eliashberg non è in grado di descrivere il comportamento del Rb3 C60 ; analogo è
il caso del K3 C60 e di moltre altre fulleriti, comprese quelle contenenti ammoniaca, le quali
mostrano inoltre ulteriori particolarità legate al cambiamento del passo reticolare.
La generalizzazione della teoria M-E consiste nell’inclusione di “correzioni al vertice” (vertex
corrections) [24, 14] nel termine dell’interazione elettrone−fonone. Rianalizzando la situazione del Rb3 C60 in questo modo, si riescono a riprodurre i dati sperimentali con valori
ragionevoli dei parametri caratteristici [10]. Tali correzioni non sono altro che i termini non
adiabatici dell’interazione, che venivano trascurati nella teoria M-E in virtù del teorema di
Migdal. In pratica questo regime non adiabatico, con un accoppiamento non troppo alto, può
essere formulato perturbativamente, al contrario della superconduttività polaronica che è intrinsecamente non perturbativa. All’ordine 0 ci si riduce naturalmente al limite M-E, mentre
la presenza di correzioni successive modifica radicalmente il significato dei soliti parametri
legati alla superconduttività, aprendo un nuovo scenario non più legato ai limiti imposti dal
teorema di Migdal. Ad esempio, in questo contesto la costante λ non caratterizza più la
forza dell’accoppiamento, dal momento che ci sono in gioco anche altri canali non adiabatici
di interazione. Questi ultimi sembrano essere responsabili di un innalzamento della Tc : il
valore della temperatura critica, che nel quadro M-E era legato a λ e quindi limitato a bassi
valori, in questo nuovo contesto può assumere valori più elevati anche per λ < 1. Nel formalismo di seconda quantizzazione sviluppato dalla teoria, le correzioni non adiabatiche vengono
rappresentate con diagrammi di Feynmann e al primo ordine perturbativo, nel parametro
λhωp i/EF , sono presenti due vertex corrections e un processo di cross phonon scattering [13].
La trattazione dettagliata del formalismo va al di fuori dell’ambito di questa tesi; il risultato
principale è che le correzioni non adiabatiche sono fortemente influenzate dai valori di momento ed energia scambiati nell’interazione. In particolare sono positive per alti valori di q e
negativi per bassi q, ciò significa che gli scattering a piccoli angoli rafforzano l’accoppiamento,
mentre quelli a grandi angoli lo indeboliscono: la ragione fisica di questo comportamento è
intimamente legata alla competizione fra la polarizzazione del reticolo indotta dagli elettroni
e gli effetti di correlazione fra di essi. È chiaro che in questo contesto tali effetti non possono
16
1. Struttura e superconduttività dei composti del C60
Figura 7: Potenziale elettrone−fonone nonadiabatico al primo ordine perturbativo: da sinistra
a destra abbiamo i diagrammi di Feynmann che rappresentano le prime due vertex corrections e
il processo di cross phonon scattering. Le linee dritte indicano la direzione di propagazione degli
elettroni, mentre quelle ondulate la propagazione dei fononi che interagiscono.
essere ridotti al semplice potenziale repulsivo coulombiano µ∗ , ma influenzano sensibilmente
l’interazione elettrone−fonone, determinando una predominanza degli eventi di scattering a
basso q. Questo può essere parametrizzato da un valore di cut-off qc del momento scambiato,
che risulta anche essere una misura della correlazione elettronica. Questa complessa interpretazione fisica delle correzioni non adiabatiche è stata discussa in dettaglio da Grimaldi,
Pietronero e Scattoni [15] che hanno separato la funzione rappresentativa delle correzioni
P (k + q, k) in due termini additivi Ppol , legato alla polarizzazione del reticolo, e Pex legato
all’interazione di scambio fra gli elettroni accoppiati. Essendo quest’ultimo, per sua natura,
coulombiano tende a indebolire l’interazione elettrone−fonone, mentre Ppol ovviamente la
rafforza. Inoltre Pex è il termine sensibile al trasferimento di momento ed energia, quindi è
quello che in base ai valori di q e ω può modificare il segno della correzione adiabatica finale:
• vF |q| ωp =⇒ P ∼ Ppol
• vF |q| ωp =⇒ P ∼ Pex
dove vF è la velocità di Fermi.
È allora possibile individuare situazioni in cui le correzioni non adiabatiche determinano un
aumento dell’accoppiamento, e quindi di Tc ; questo succede ogni qualvolta gli effetti di scambio diventano meno importanti, ad esempio nel caso in cui la densità di carica al livello di
Fermi sia bassa, e quindi la distanza media fra gli elettroni sia tale da indebolire molto lo
scambio. Questa è proprio la situazione delle fulleriti A3 C60 che sono solidi molecolari: la
presenza di superconduttività in questi materiali sembrava un’anomalia all’interno del quadro
M-E, perchè il basso numero di portatori di carica, schermando la repulsione coulombiana
in modo inefficiente, sfavoriva la formazione di coppie di Cooper. Paradossalmente, lo stesso
meccanismo che nella teoria M-E sfavorisce la superconduttività delle fulleriti, nel contesto
nonadiabatico assume un ruolo contrario e porta ad una spiegazione meno artificiale della fe-
1.3. Superconduttività
17
nomenologia. In conclusione, la teoria nonadiabatica apre un nuovo scenario per la superconduttività, dove i nuovi canali d’accoppiamento disponibili portano al superamento dei limiti
imposti dalla teoria di Migdal-Eliashberg: abbiamo visto che danno la possibilità di alzare Tc ,
anche in presenza di valori standard dei parametri classici, λ ∼ 0.6 − 0.8, µ ∼ µ∗ ∼ 0.4 − 0.5;
inoltre ci sono una serie di predizioni specifiche su grandezze fisiche estranee al contesto M-E,
la misura delle quali quindi costituisce un ottimo test di consistenza per la teoria stessa. In
particolare, molte previsioni riguardano l’effetti isotopici su svariate grandezze fisiche nella
fase normale, fra cui Tc , la massa efficace degli elettroni accoppiati m∗ e la suscettibilità di
spin χ [12].
1.3.2.2
Suscettibilità di spin χ in regime nonadiabatico
La suscettibilità di spin è una proprietà non particolarmente interessante in regime M-E, il cui
comportamento si modifica in regime nonadiabatico, pertanto la misura della suscettibilità
paramagnetica di Pauli χ può essere considerata una prova del breakdown del teorema di
Migdal. In regime M-E l’interazione elettrone−fonone non influenza χ, cosı̀ questa risulta
indipendente da λ e ωp , e si può scrivere semplicemente χ ≡ χp = µ2B N (0). Di conseguenza
una misura di questa χ fornisce in linea di principio il valore della densità degli stati. Il fatto
interessante è che dal momento in cui ωp /EF non risulta più trascurabile, χ comincia a sentire
l’influenza fononica, quindi diventa dipendente da λ e ωp ; questo può essere importante per
due motivi:
• porta a riconsiderare la stima della densità degli stati elettronici da sempre basate
sull’indipendenza di χ dal meccanismo fononico d’accoppiamento.
• la rinormalizzazione nonadiabatica di χ induce un effetto isotopico che può essere
misurato.
Come si vede dai grafici in figura 8, in cui è mostrato l’andamento, a temperature prossime allo zero assoluto, della suscettività di Pauli calcolata, il risultato principale dei calcoli
nonadiabatici preliminari è che χ(0)/χp < 1 quanto più ωp /EF cresce; calcoli con incluse le
correzioni non adiabatiche di ordini successivi confermano questo risultato [8]. La riduzione
di χ per via dell’interazione elettrone−fonone nel caso in cui ωp /EF assuma valori finiti, porta
a riconsiderare le stime della densità degli stati ottenute da misure EPR; i valori sperimentali
di suscettività venivano fittati con l’espressione M-E per χ:
χ ∝ N (0) ∼
N0 (0)
,
1−I
(9)
dove N (0) è stato esplicitamente separato in N0 (0), densità di stati per elettroni liberi, e nel
fattore 1/(1 − I) che tiene conto degli effetti a molti elettroni (fattore di Stoner).
18
1. Struttura e superconduttività dei composti del C60
Figura 8: Caratteristica della suscettibilità χ in funzione di λ (a sinistra) e di ωp /EF (a destra).
Grazie a stime teoriche di questo fattore risulta possibile ottenere N0 (0) dai dati sperimentali; tuttavia questa procedura porta ad una sottostima di N0 (0) se ωp /EF non è trascurabile,
come per le fulleriti. In base a quanto detto fino ad ora, N0 (0) dell’equazione (9) dovrebbe
essere rimpiazzato con N0∗ (0) ' N0 (0)f (λ, ωp /EF ), dove la funzione f tiene in considerazione la rinormalizzazione di χ dovuta all’interazione elettrone−fonone, ed è minore dell’unità.
Dalla figura 8 risulta anche evidente che un aumento di ωp causa una diminuzione di χ; tale
variazione può ad esempio essere causata dalla sostituzione di un isotopo, quindi siamo di
fronte ad un evidente effetto isotopico su χ, il cui andamento dipende da αχ :
αχ = −
d ln χ
1 d ln χ
=
d ln M
2 d ln( EωFp )
Figura 9: Coefficiente isotopico αχ della suscettibilità in funzione del parametro di adiabaticità
ωp /EF per differenti valori di λ.
(10)
1.3. Superconduttività
19
dove M è la massa dello ione. La figura 9 rappresenta una valutazione numerica dell’equazione
(10) in funzione di ωp /EF e per differenti valori del parametro λ. Come ci si aspetta αχ
si annulla nel limite adiabatico, mentre in regime non adiabatico diventa negativo e per
valori di λ ordinari è circa 0,05. Per quanto sia un valore basso, qualora fosse misurato
rappresenterebbe comunque un chiaro riscontro della nonadiabaticità: per questo motivo è
molto importante indagare l’eventuale presenza o assenza di un simile effetto isotopico sulle
fulleriti superconduttive. Il risultato di questo genere di esperimento fornirebbe una stima di
ωp /EF , quindi una stima del grado di nonadiabaticità di questi composti.
20
1. Struttura e superconduttività dei composti del C60
Capitolo 2
Tecniche sperimentali
2.1
Magnetometria SQUID
Il comportamento magnetico del K3 C60 è stato studiato tramite un magnetometro SQUID,
in quanto misure di magnetometria convenzionali si presentano difficili su campioni come le
fulleriti, il cui debole magnetismo richiede un’alta sensibilità.
Gli SQUID sono fra gli strumenti a più alta sensibilità mai costruiti potendo misurare anche
campi dell’ordine dei pT. La parte di rivelazione è costituita da un anello di materiale superconduttore tenuto a ∼4.2 K, interrotto in due punti da un sottile strato isolante (giunzioni
Josephson), in modo da separare l’anello in due regioni superconduttrici distinte, I e II (vedi
figura 10(a)). Il dispositivo sfrutta un effetto di interferenza quantistica fra le supercorrenti,
le quali attraversano anche lo strato isolante per effetto tunnel delle coppie di Cooper. Il fatto
che il funzionamento dello SQUID non venga compromesso anche se la separazione spaziale
fra le due giunzioni Josephson risulta estesa per qualche centimetro, significa che la coerenza
della funzione d’onda dello stato superconduttivo si mantiene a distanza: questo è un esempio
di manifestazione macroscopica della coerenza quantistica dei portatori.
Il comportamento delle funzioni d’onda in presenza di una barrriera di potenziale è mostrato in figura 10(b); Per una barriera di larghezza l con estremi nei punti ±l/2, la funzione
d’onda nella generica posizione x può essere semplicemente scritta come la somma dei due
contributi delle due regioni superconduttrici:
ψ=
n 2 h
s
2
ei θ1 −α(x+l/2) + ei θ2 −α(x−l/2)
i
,
(11)
dove ns è la densità delle coppie di Cooper. La densità di supercorrente attraverso la giunzione
può essere valutata utilizzando la relazione:
j(r) =
2e2 ∗
i~e ∗
(ψ ∇ψ − ψ∇ψ ∗ ) −
ψ ψA ,
2me
me
21
(12)
22
2. Tecniche sperimentali
Figura 10: Schema di principio di uno SQUID (a), e sovrapposizione delle funzioni d’onda
all’interno di una barriera di potenziale (b).
dove A è il potenziale vettore tale da luogo al campo magnetico B = ∇ × A. Nel caso in cui
A=0 otteniamo:
j = j0 sin δ ,
dove j0 =
~ e ns
me
(13)
α e−αl e δ = θ2 − θ1 è la differenza di fase fra le due regioni superconduttrici
separate dalla giunzione.
La rappresentazione schematica di uno SQUID è mostrata in figura 10(a): la supercorrente viene suddivisa in due componenti Ia e Ib , ciascuna delle quali incontra una giunzione
Josephson. Le supercorenti nella regione I del dispositivo, prima della suddivisione, e nella
regione II, dopo la ricombinazione, sono uguali a meno della differenza di fase δ causata dalla
presenza della barriera di potenziale fra le regioni stesse (assumiamo identiche le due giunzioni a e b in modo che δa = δb = δ). La presenza di un campo magnetico nell’area racchiusa
dal dispositivo causa ulteriori sfasamenti che determinano un modulazione periodica della
supercorrente al variare del campo secondo la relazione:
I = Ia + Ib = 2Aj0 cos(e Φ/~) sin δ ,
(14)
dove A è l’area delle giunzioni e Φ = nΦ0 , essendo Φ0 il quanto di flusso magnetico, Φ0 = h/2e.
Questa dipendenza permette di misurare campi magnetici estremamente piccoli.
2.1.1
Metodologia di misura
Il magnetometro SQUID si basa sulla giunzione Josephson descritta nella sezione precedente.
In pratica il flusso magnetico da misurare modula la corrente attraverso la giunzione e tale
modulazione viene rilevata e amplificata dall’elettronica dello strumento.
A seconda della
tensione applicata gli SQUID si suddividono in due tipi: in corrente alternata (AC, oppure
RF), e in corrente continua (DC).
2.1. Magnetometria SQUID
Figura 11: Struttura di un magnetometro SQUID. La bobina in cui è immerso il campione è
strutturata in modo tale da sottrarre il flusso di campi esterni che influenzerebbe le misure.
23
24
2. Tecniche sperimentali
Nonostante gli SQUID di tipo AC siano più facili da costuire e usare, il funzionamento dello
SQUID DC è più semplice da capire ed è quindi ad esso che ci riferiamo in seguito.
La struttura di un magnetometro SQUID è presentata in figura 11, mentre lo schema
elettronico dell’intero dispositivo è presentato in figura 12. Per avere una elevata sensibilità
ai campi magnetici si utilizza un contorno a flusso fissato (flux-locked loop), in cui la corrente
di retroazione agisce in modo da tenere sempre costante il flusso attraverso lo SQUID. Una
configurazione con un amplificatore di tipo lock-in e il trasformatore in uscita dello SQUID
provvedono entrambi ad avere un buon rapporto segnale/rumore.
In sostanza il dispositivo SQUID si comporta come un convertitore flusso (corrente)tensione. Il segnale magnetico viene rilevato da una bobina avente quattro spire in configurazione di gradientometro di secondo ordine (vedi figura 11), la quale è accopiata allo
SQUID vero e proprio. Tale configurazione, pur non avendo la massima sensibilità, presenta
un elevato livello di immunità dal rumore elettromagnetico (sia da quello dovuto al magnete
fisso che da quello proveniente da campi esterni). In tal modo lo SQUID può essere posto
ad una certa distanza ed opportunamente schermato dai campi esterni, avendo come unico
accopiamento con l’esterno quello con i flussi magnetici che interessano la bobina.
Muovendo il campione attraverso la bobina rilevatrice si ha una variazione del flusso
magnetico attraverso le spire, il quale induce una tensione in uscita. Il flusso attraverso una
spira di raggio R, dovuto ad un dipolo magnetico m giacente sul suo asse e distante x dal
piano della spira si calcola facilmente usando l’espressione in coordinate polari del campo
magnetico dipolare e il fatto che B è un campo solenoidale (assenza di monopoli magnetici).
Esso è dato dall’espressione:
ΦB =
R2
µ0 m
.
· 2
2
(x + R2 )3/2
(15)
(a)
Ib
Amplifier
Mf
Integrator
Lock-in
detector
∫
SQUID
Oscillator
fM
Rf
Feedback + Modulation
Feedback
Figura 12: Schema di uno SQUID DC
(b)
SQUID Controller
Flux-locked
loop
I
V
B
Vout
Vout
25
2.2. Fondamenti di risonanza magnetica nucleare NMR
Dato che le spire della bobina sono in serie e montate come mostrato in figura 11, il flusso
totale in funzione della distanza dal centro della bobina sarà dato dalla somma algebrica di
termini del tipo (15). Quindi all’uscita dello SQUID il segnale amplificato in funzione della
posizione del campione avrà un andamento:
V (x) ∝
4
−3/2
µ0 mR2 X (x + di )2 + R2
,
2
(16)
i=1
con di rispettivamente +a, +b, −b e −a e il segno dei termini riguardanti le spire poste a
distanza a opposto a quelle a distanza b.
La misura si fa posizionando in successione il campione a varie distanze dal centro della
bobina (scan) e rilevando il valore di tensione V (z) rispettivo. In caso di campioni con
magnetizzazione molto esigua più acquisizioni sono necessarie affinché il segnale abbia un
livello accettabile di S/N. Il computer interfacciato allo strumento esegue infine un algoritmo
di regressione lineare dal quale si può dedurre il valore del momento m. I valori misurati
assieme al fit con una curva del tipo (16) sono mostrati in figura 13.
1
Signal (arb. units)
0.5
0
−0.5
−1
−1.5
−2
−5
−4
−3
−2
−1
0
1
2
3
4
5
Scan distance (cm)
Figura 13: Segnale SQUID mentre il campione (diamagnetico) si muove attraverso una bobina
rivelatrice in configurazione di gradientometro di secondo ordine. Le posizioni delle quattro
spire sono mostrate in alto. Dalla curva di miglior fit (tratto continuo) si ottiene il valore di
magnetizzazione m del campione.
2.2
Fondamenti di risonanza magnetica nucleare NMR
La risonanza magnetica riguarda l’assorbimento di energia elettromagnetica che si ha quando
elettroni o nuclei, dotati di momento magnetico proprio ed immersi in un campo magnetico
statico H0 , sono sottoposti ad un campo magnetico variabile di frequenza uguale o molto prossima alle differenze di livelli energetici del sistema. Grazie al fenomeno della risonanza, si può
26
2. Tecniche sperimentali
osservare il magnetismo nucleare altrimenti completamente mascherato dal paramagnetismo
e diamagnetismo elettronico, più intensi di almeno 3 ordini di grandezza (µN /µB ∼ 10−3 ).
In questo caso si parla di Risonanza Magnetica Nucleare (NMR) e le frequenze di risonanza
giacciono nel campo delle radioonde. Con questa tecnica è possibile ottenere informazioni
non soltanto sui nuclei, ma anche sull’ambiente elettronico circostante.
La tecnica NMR si basa sul fatto che il modo in cui il materiale restituisce l’energia
elettromagnetica assorbita può fornire informazioni su varie proprietà del materiale stesso.
Nella visione quantomeccanica, un fenomeno di risonanza rappresenta una transizione fra due
livelli energetici. In un trattamento semiclassico, invece, un generico spin S sottoposto ad
un campo magnetico H0 , diretto lungo z, precede attorno alla direzione del campo ad una
frequenza caratteristica ω0 = γH0 . Utilizzando una bobina posta nel piano x-y e sottoposta
ad una differenza di potenziale alternata di frequenza ω0 , si genera un campo magnetico
polarizzato linearmente che a sua volta si può vedere come la sovrapposizione di due campi
con polarizzazione circolare e rotanti in verso opposto. Se consideriamo solo la componente
rotante H1 , equiversa alla precessione di S, il suo effetto è quello di piegare lo spin, cioè
scambiare energia col sistema magnetico. Questo avviene perchè istante per istante la forza
esercitata dal campo rotante segue la rotazione dello spin attorno ad H0 con la stessa fase. Il
fenomeno si può analizzare efficacemente in un sistema di riferimento rotante alla frequenza
ω0 : in tale sistema l’unico campo magnetico applicato è H1 che risulta fisso. H0 , al contrario,
non è presente in quanto il suo effetto (la rotazione) è tenuto in conto dal sistema di riferimento
non inerziale rotante. In tale sistema, l’applicazione del campo H1 induce una rotazione dello
spin secondo la legge ω1 = γH1 . In seguito, per la rivelazione della precessione, si sfrutta il
fenomeno dell’induzione sulla stessa bobina d’irraggiamento. Per avere il massimo di segnale,
lo spin S deve precedere nel piano della bobina e per ottenere ciò è sufficiente una rotazione
di 90◦ (o in generale di (k + 1/2)π) attorno al campo H1 che si realizza nel tempo τ =
π
2γH1 .
In realtà, questa spiegazione qualitativa è molto semplicistica e non tiene conto di fattori
che nei sistemi reali determinano lo smorzamento della f.e.m. indotta. Dato che il segnale
di precessione è costituito dalla somma dei segnali provenienti dai diversi spin, esso decade
in seguito alla decoerenza degli spin dovuta alla disomogeneità del campo o a fenomeni
irreversibili come i rilassamenti spin-spin e spin-reticolo, dei quali si parlerà in seguito.
Il segnale indotto nella bobina viene comunemente chiamato FID (Free Induction Decay)
ed è generalmente di tipo esponenziale, quindi la relativa trasformata di Fourier risulta essere
una lorenziana, che nella sua forma normalizzata si scrive:
L(ω) =
1
1
2Γ
π (ω − ω0 )2 +
2
1
2Γ
,
dove Γ è la larghezza a metà altezza.
(17)
27
2.2. Fondamenti di risonanza magnetica nucleare NMR
2.2.1
Interpretazione semiclassica
Applicando la seconda equazione cardinale della dinamica classica ad una particella con momento magnetico intrinseco µ = γJ sottoposta ad un campo magnetico statico uniforme H0 ,
convenzionalmente orientato lungo z, si ottiene l’equazione della precessione con frequenza
ω0 = γH0 :
dJ
= µ × H0
dt
−→
dµ
= γµ × H0
dt
−→
dµ
= −γH0 × µ .
dt
(18)
Se µ possiede una componente perpendicolare a z, essa comincia a precedere attorno ad H0
con frequenza ω0 ; inoltre l’angolo che µ forma con l’asse z rimane sempre fisso finchè non vi
è scambio di energia con l’ambiente esterno (vedi figura 14).
Figura 14: Precessione del momento magnetico µ attorno all’asse z: il vettore descrive un cono
il cui angolo θ rispetto alla verticale rimane invariato. La direzione di precessione mostrata è
quella di un nucleo con rapporto giromagnetico γ positivo.
Se si aggiunge un campo magnetico variabile H1 polarizzato circolarmente nel piano x-y:
H1 (t) = H1 cos ωt i − H1 sin ωt j ,
(19)
la descrizione del fenomeno nel sistema non inerziale solidale con H1 (t) risente della presenza
della velocità di trascinamento ω × r, cosı̀ l’equazione del moto in questo sistema si modifica
tenendo conto della legge che lega le derivate temporali fra un sistema inerziale e un sistema
non inerziale rotante a velocità costante ω:
dµ
dµ
=
+ω×r ,
dt S
dt S 0
dove con
S
si indica la rappresentazione della grandezza nel sistema inerziale, e con
(20)
S0
la rappresentazione della stessa nel sistema rotante. Ponendo nell’equazione (18) il campo
uguale a H(t) = H0 + H1 (t) e tenendo conto della relazione (20), si ottiene:
dµ
dt
S0
ω
= µ × (γH + ω) = H1 cos ωt i − H1 sin ωt j + H0 −
k
γ
(21)
28
2. Tecniche sperimentali
Figura 15: Traiettoria del momento magnetico µ nel sistema del laboratorio: è la composizione
della precessione attorno a z e di quella più lenta attorno all’asse rotante x0
Per semplicità scegliamo S 0 in modo che l’asse x0 sia solidale con H1 (t); si può definire allora
un campo efficace, che è quello percepito dal momento magnetico µ nel sistema rotante:
ω
0
Hef f = H1 i + H0 −
k.
(22)
γ
In base al valore di ω, Hef f potrà risultare parallelo o perpendicolare a z. Fuori risonanza
il valore di campo efficace è generalmente dominato da H0 , in quanto H0 H1 e lo spin
descrive un cono molto stretto attorno ad Hef f . In risonanza (ω = ω0 ) si ha la condizione
particolare in cui la componente z di Hef f , cioè H0 , si annulla; allora il moto del momento
magnetico in S 0 si riduce ad una precessione attorno all’asse x0 , mentre nel sistema inerziale
S si ha un moto formato dalla composizione di due precessioni, di cui la seconda attorno ad
un asse rotante (vedi figura 15).
È evidente che per questo effetto l’angolo θ formato da µ con l’asse z cambia continuamente;
inoltre, siccome E = µ · H = µH cos θ, il sistema magnetico scambia continuamente energia
con “l’ambiente” attraverso il campo esterno H1 .
2.2.2
Interpretazione quantistica
L’Hamiltoniana che descrive l’interazione fra un nucleo isolato, dotato di momento magnetico
µ = γJ = γ~I e il campo magnetico H0 , in cui esso è posto, è la seguente:
H = −µ · H0 = −γ~H0 Iz ,
(23)
dove i 2I + 1 autovalori sono dati da:
Em = −γ~H0 m
m = −I, ..., I .
(24)
L’introduzione del piccolo campo H1 non rappresenta altro che una perturbazione del sistema
costituito dal momento magnetico µ posto in un campo H0 ,
Hper = −γH1 Ix cos ωt ,
(25)
2.2. Fondamenti di risonanza magnetica nucleare NMR
29
quindi in prima approssimazione, il suo effetto è quello di indurre transizioni fra gli autostati dell’hamiltoniana (23). Trattare il sistema in termini perturbativi costituisce l’analogo
quantistico di considerare la precessione attorno all’asse rotante x0 (nutazione) più lenta della
precessione attorno all’asse z. La condizione richiesta è in entrambi i casi H0 H1 . Data
l’equivalenza dei due trattamenti appena descritti, in un approccio sperimentale è spesso più
utile fare riferimento alla visione classica del fenomeno la quale, peraltro, in molti casi risulta
effettivamente valida per i valori medi degli operatori quantistici, come ci si aspetterebbe in
casi semplici dal teorema di Ehrenfest [6, 26].
2.2.3
Sistemi macroscopici di spin
Vediamo ora di generalizzare la trattazione classica della dinamica del singolo spin in modo
da poter includervi anche i parametri macroscopici del sistema, come la magnetizzazione
e la suscettività. È evidente che l’equazione della precessione (18) non è immediatamente
generalizzabile alla magnetizzazione M dei sistemi reali, infatti moltiplicando scalarmente
l’equazione (18) per M si otterrebbe
1 dM 2
=M·
2 dt
dM
dt
= M · M × γH = 0 ,
(26)
non potendo quindi variare il modulo di M il materiale non si magnetizzarebbe mai, il che è
chiaramente contrario all’evidenza sperimentale. La semplicistica generalizzazione a M della
equazione (18) non può in alcun modo descrivere la fenomenologia, per spiegare la quale
è necessario partire da argomentazioni di termodinamica. Il sistema di spin non è isolato,
ma è immerso in un bagno termico costituito dal reticolo che, in presenza di un campo
magnetico statico, determina la popolazione dei vari livelli secondo la statistica di Bolzman,
e di conseguenza la magnetizzazione M, secondo la legge:
I
X
M = N γ~
m=−I
I
X
me
γ~mH0
kT
(27)
e
γ~mH0
kT
m=−I
Em
dove N è il numero di spin ed Em ∝ e− kT il livello m-esimo di energia del singolo spin.
Le vibrazioni reticolari e l’insieme degli elettroni costituiscono un vero e proprio termostato
per in sistema magnetico e sono responsabili dei fenomeni di rilassamento nucleare che tendono a riportare la magnetizzazione in equilibrio.
A questo proposito Bloch propose, nel 1946, un insieme di equazioni fenomenologiche che forniscono in molti casi (in particolare nei sistemi amorfi e nei liquidi) una descrizione corretta
dei rilassamenti. Esse tengono conto di due aspetti:
30
2. Tecniche sperimentali
• Scambio di energia con qualche sistema fisico esterno all’insieme degli spin nucleari
(termostato elettronico e vibrazioni reticolari).
• Ripartizione dell’energia fra i vari momenti magnetici con tempi caratteristici propri.
Se il sistema magnetico (nuclei nel campo applicato) fosse isolato, la magnetizzazione non
potrebbe variare il suo modulo, quindi per rendere possibili variazioni di M conviene riferirsi,
in analogia con un sistema a due livelli, all’equazione:
n0 − n
dn
=
,
dt
T1
(28)
dove n = N+ − N− è la differenza di popolazione fra i due livelli che dà luogo al vettore
magnetizzazione macroscopica M. Di conseguenza:
dMz
M0 − Mz
=
dt
T1
(29)
con M0 il valore della magnetizzazione all’equilibrio (M0 = χ0 H0 ). Combinando questa
equazione con la (18) otteniamo la prima equazione di Bloch che determina il trasferimento
di energia, introducendo un termine di rilassamento T1 :
dMz
M 0 − Mz
= −γ(H0 × M)z +
.
dt
T1
(30)
Il tempo T1 assume innanzitutto il significato di una costante di tempo, caratteristica del
rilassamento di Mz , quando, integrando la (29), si ottiene:
− Tt
1
M z = M0 1 + e
.
(31)
Inoltre, a differenza delle altre costanti di tempo che descrivono rilassamenti di tipo trasversale, essa rappresenta quei meccanismi di scambio energetico con il termostato esterno al
mondo magnetico che permettono alla magnetizzazione di ritornare al suo valore di equilibrio
M0 .
Per esprimere il fatto che all’equilibrio M è parallela a H0 è necessario imporre che la magnetizzazione trasversale tenda a 0 dopo un tempo sufficientemente lungo, il che porta alle
altre due equazioni di Bloch.
dMx
dt
dMy
dt
Mx
,
T2
My
= −γ(H0 × M)y −
.
T2
= −γ(H0 × M)x −
(32)
(33)
La presenza dello stesso tempo di rilassamento T2 sia per x che per y è giustificata dal fatto
che le eventuali anisotropie tra le due direzioni trasversali vengono mediate a zero dal moto
di precessione, quindi, nella maggioranza dei casi, ha senso parlare solo di magnetizzazione
trasversale, e non di Mx e My separatamente. Solo nel caso in cui i rilassamenti trasversali
31
2.3. Fenomeni di rilassamento
siano più veloci del moto di precessione attorno a z, ha senso tenere in considerazione una
eventuale anisotropia fra x e y. Al contrario, è fondamentale sottolineare la differenza fra
i meccanismi responsabili dei rilassamenti di tipo T1 e T2 : in quest’ultimo caso Mxy → 0
senza bisogno di alcuno scambio energetico col termostato esterno; il fenomeno avviene solo
ed esclusivamente a causa di quei processi interni al sistema magnetico che fanno perdere
coerenza al moto complessivo dei momenti magnetici (per esempio, la presenza di diverse
frequenze di precessione causate da disomogeneità di campo, ecc.).
2.3
Fenomeni di rilassamento
Per descrivere più approfonditamente la dinamica della magnetizzazione ed i suoi tempi caratteristici, è opportuno riassumere prima le caratteristiche principali di un tipico esperimento
NMR. Per fare questo, ci si avvale generalmente della visione classica in quanto più intuitiva.
La tecnica utilizzata è quella dell’NMR a impulsi, nella quale si eccitano i campioni tramite impulsi di radiofrequenza di durata limitata, controllabile via software, e si alternano in
modo opportuno tempi d’irraggiamento e ritardi in modo da costruire diverse sequenze, cioè
diversi tipi d’esperimento. Va sottolineato che il campo rotante H1 è in realtà ottenuto tramite una normale bobina, ortogonale all’asse z, la quale genera quindi un campo polarizzato
linearmente; questo può essere pensato come la composizione di due componenti con polarizzazioni circolari di frequenza ±ω0 , cioè una rotante in verso opposto all’altra. Di queste due
componenti solo una andrà in risonanza, l’altra, invece, causerà solo effetti trascurabili. Gli
impulsi utilizzati vengono classificati in base all’angolo di rotazione di cui possono piegare la
magnetizzazone del campione:
applicazione di un impulso
π
2
π
2 , π,
ecc. Il tipico esperimento NMR consiste nella semplice
e la conseguente rivelazione del segnale di rilassamento trasver-
sale, free induction decay (FID). Lo studio della forma del FID e della relativa trasformata
di Fourier sono la base da cui parte un’analisi NMR.
2.3.1
Rilassamento spin-spin
Il decadimento della magnetizzazione trasversale durante la precessione attorno a z è dovuto
principalmente a due fattori:
• Disomogeneità del campo.
• Interazione dipolare diretta fra momenti magnetici vicini, nota come interazione spinspin.
Ci possono essere anche altri contributi al rilassamento spin-spin, come l’interazione elettrostatica fra il quadrupolo nucleare e il gradiente di campo elettrico al nucleo (presente in
nuclei aventi I > 1/2 posti in un circondario elettronico a bassa simmetria), oppure si può
32
2. Tecniche sperimentali
presentare la situazione in cui il decadimento è legato alla vita media dei livelli energetici,
intimamente connessa con T1 . Trascurando l’accoppiamento quadrupolare e altri eventuali
accoppiamenti anisotropi generalmente mediati a zero in campioni policristallini o polveri,
possiamo scrivere in forma abbastanza generale:
1
1
1
=
+
+ γ∆H
∗
T2
2T1 T2
(34)
dove T2∗ rappresenta il tempo di rilassamento efficace comprendente i vari contributi che in
questo caso si riducono a 3:
1
T2
1
2T1
1. Allargamento dovuto all’interazione spin-spin
, unico termine considerato nella
trattazione semplificata del paragrafo 2.2.3.
2. Termine collegato alla vita media dei livelli
, generalmente trascurabile rispetto
agli altri.
3. Disomogeneità del campo magnetico γ∆H, responsabile della presenza di più frequenze
di risonanza all’interno del campione.
L’ultimo termine agisce generando uno sfasamento fra spin veloci e lenti che quindi non si
sommano più in fase, determinando cosı̀ una progressiva diminuzione della magnetizzazione
trasversale. È da notare che anche l’interazione spin-spin determina uno sparpagliamento
degli spin ma in modo disordinato: essa opera a livello microscopico in modo meno deterministico ed è quindi irreversibile (in senso termodinamico), mentre lo sparpagliamento della
disomogeneità del campo avviene su una scala macroscopica ed è dovuto alla precessione; dunque la possibiltà di invertirlo non sembra cosı̀ remota. In effetti, esistono sequenze particolari
di impulsi (spin-eco) le quali, basandosi su questa diversità, in particolare sulla reversibilità dell’effetto di γ∆H, riescono ad eliminare l’influenza di quest’ultimo, permettendoci di
estrarre direttamente l’informazione sul T2 omogeneo. La più semplice sequenza di spin eco
è rappresentata dall’eco di Hahn (vedi figura 16), costituita da due impulsi, rispettivamente
di
π
2
e π, intervallati da un ritardo τ . Dopo il primo impulso, che piega la magnetizzazione
sull’asse x0 , in assenza di disomogeneità di campo ∆H, essa rimarrebbe sempre su questo
asse decadendo solo per fenomeni di rilassamento irreversibili; invece per ∆H 6= 0 ci saranno
spin che precedono in anticipo (con ∆ω+ = γ∆H/2) e altri in ritardo (con ∆ω− = −γ∆H/2).
Dato che questo è un fenomeno reversibile, se si applica un secondo impulso di π si capovolge
la magnetizzazione da +x0 a −x0 . A questo punto gli spin prima in ritardo di ∆φ risultano
essere in anticipo della stessa quantità, mentre, analogamente, quelli che erano in anticipo
si trovano in ritardo. Dal momento che la velocità di precessione di ciascuna componente
della magnetizzazione rimane invariata nonostante il ribaltamento, l’evoluzione temporale
di questa situazione porta, dopo un tempo proporzionale a ∆φ, alla rifocalizzazione di spin
33
2.3. Fenomeni di rilassamento
Figura 16: Rappresentazione del ribaltamento delle componenti della magnetizzazione trasversale in seguito ad un impulso π. Se per semplicità si suddividono gli spin nei 3 gruppi con diversa
velocità rappresentati in figura, nel sistema di riferimento solidale con i momenti che precedono
a velocità intermedia si vedono, in anticipo e in ritardo rispettivamente, la componente della
magnetizzazione formata dagli spin più veloci e quella formata dagli spin più lenti. Immaginando la magnetizzazione M come combinazione di questi 3 vettori e ribaltando gli stessi rispetto
all’asse y senza cambiare la direzione di precessione, si ottiene il rifasamento degli spin. È chiaro
che solo per la componente che precede alla velocità intermedia il ribaltamento è esattamente
di 180◦ , per le altre due l’impulso di π risulta un po’ minore di 180◦ .
veloci e lenti assieme a quelli di velocità intermedia. In seguito gli spin cominciano di nuovo
a sfasarsi causando l’estinzione del segnale. Con questa sequenza al variare del ritardo τ
fra i due impulsi si può misurare il tempo caratteristico T2 , cioè il rilassamento trasversale
intrinseco, senza il contributo dovuto alla disomogeneità del campo. Come già accennato,
nella maggior parte dei casi il decadimento della magnetizzazione è esponenziale nel tempo.
Ciò corrisponde, nello spazio delle frequenze, ad avere una riga lorenziana la cui larghezza a
metà altezza (FWHM) risulta essere proprio
2
T2∗ ;
a volte il decadimento risulta essere gaus-
siano, e quindi anche la riga nello spazio di Fourier è gaussiana con larghezza invertita. È
evidente quindi che qualitativamente a FID rapidi corrispondono righe larghe e a FID lenti
corrispondono righe strette.
2.3.2
Rilassamento spin-reticolo
Normalmente si considerano appartenere alla categoria dell’interazione spin-reticolo tutti quei
canali di interazione che mediano l’accoppiamento fra il sistema magnetico e il circondario
elettronico dei nuclei. Questo, cosiddetto “termostato esterno” al sistema di spin, è in grado
di fornire quantità di energia da considerarsi grandi per le energie in gioco nel magnetismo
nucleare, ma piccole rispetto alla scala caratteristica delle dinamiche elettroniche.
34
2. Tecniche sperimentali
L’interazione spin-reticolo comprende dunque tutte quelle interazioni che mediano il passaggio
verso una situazione d’equilibrio in cui la magnetizzazione è del tutto rilassata lungo la
direzione del campo. I principali contributi sono:
• Interazione dipolare diretta: se i nuclei sono abbastanza vicini (e nel caso dei fullereni è
proprio cosı̀) i rispettivi campi dipolari sono abbastanza intensi da influenzarsi a vicenda. Questa interazione, oltre a contribuire al rilassamento T2 , creando una condizione
di disordine trasversale fra gli spin, costituisce anche un canale di scambio energetico col termostato esterno, e quindi contribuisce al rilassamento della magnetizzazione
verticale. In tal caso i moti traslazionali, vibrazionali, rotazionali del materiale e l’accoppiamento spin-spin si modulano reciprocamente, e durante questo processo avviene
lo scambio energetico. È chiaro che, se le interazioni magnetiche sono più intense, tale
meccanismo è più efficace; questo rende evidente l’importanza dell’interazione dipolare
diretta per il rilassamento spin-reticolo.
• Interazione quadrupolare: si ha quando il momento di quadrupolo Q è diverso da zero
e, a causa delle vibrazioni reticolari, si genera una fluttuazione del gradiente di campo
elettrico alla posizione del nucleo, che è la grandezza fisica con cui Q interagisce. Di
conseguenza anche l’interazione quadrupolare modula ed è modulata dalla dinamica
reticolare.
• altre interazioni anisotrope come il Knight shift e il chemical shift.
Tutti questi casi, a parte quello del Knight shift, rappresentano una condizione in cui il
campo fluttuante deriva da moti molecolari; l’interazione di Knight shift, al contrario, per
sua natura prescinde dal circondario elettronico locale e riguarda la risposta magnetica degli
elettroni di conduzione. Una delle tecniche che si usano per misurare il tempo caratteristico
T1 del rilassamento spin-reticolo è quella chiamata inversion recovery: si applica un impulso
di π in modo da portare la magnetizzazione sull’asse -z; a questo punto M è molto lontana
dalla condizione d’equilibrio e quindi impiega un certo tempo ad evolvere, finchè non si riporta
lungo la direzione +z. Se, durante questo periodo di tempo, dopo un certo ritardo τ dal primo
impulso, si eccita il sistema con un impulso di
π
2,
allora si riporta in direzione trasversale la
magnetizzazione che ha avuto modo di avere un rilassamento verticale durante l’intervallo
di tempo τ . Se si ripete questa sequenza più volte variando il ritardo fra i due impulsi, si
ricostruisce l’andamento nel tempo del modulo di M e quindi si misura T1 .
La legge che governa il fenomeno è esponenziale ed obbedisce all’equazione
h
τ i
−
M (t) = M0 1 − 2 e T1
.
(35)
Quando il rilassamento è legato a più effetti concomitanti, il tempo T1 assume il significato
di valor medio dei vari contributi, ed in alcuni casi l’equazione (35) non è più valida.
35
2.4. Interazioni di base in NMR dello stato solido
2.4
Interazioni di base in NMR dello stato solido
Gli spettri NMR di soluzioni sono spesso costituiti da righe molto strette, in quanto il moto casuale delle molecole (fast tumbling) media a zero il contributo delle interazioni NMR
anisotrope. Al contrario, gli spettri NMR di campioni allo stato solido sono spesso molto
larghi, infatti l’osservazione degli effetti anisotropi sulla forma di riga è proprio quello che
interessa in NMR di stato solido: la presenza di righe larghe fornisce molte informazioni sia
NMR Interactions in the Solid State
di tipo chimico, sia riguardo la dinamica del campione. Ad esempio, essa permette di scoprire
l’evoluzione dinamica del materiale al variare della temperatura con eventuali transizioni di
fase (proprio come nel caso del reticolo fcc di C60 , vedi paragrafo 1.2). I possibili canali
In d’accoppiamento
the solid-state,
there are seven ways for a nuclear spin to
fra sistema magnetico e campi esterni sono schematizzati in figura 17.
communicate with its surroundings:
6
Electrons
3
1
Nuclear spin I
5
2
4
3
Nuclear spin S
1
4
Phonons
1:
2:
3:
Figura 17: Rappresentazione dei principali canali d’interazione fra sistema magnetico di spin e
Zeeman
interaction
spins
campi esterni applicati,
rappresentatiof
con nuclear
cerchio esterno:
(1) interazione Zeeman; (2) interazione dipolare diretta; (3) interazione dipolare indiretta (J-coupling); (4) interazione spin-reticolo
Direct
dipolar spin interaction
diretta; (3-5) interazione spin-reticolo indiretta; (3-6) schermo chimico.
Indirect spin-spin coupling (J-coupling), nuclear-electron
spin sulla
coupling
(paramagnetic),
coupling
ofrilevanti
nuclear
Basandoci
figura 17, consideriamo
più in dettaglio
le interazioni
per lespins
misure with
effettuate
sui campioni
di K3 C60 . field gradients (quadrupolar interaction)
molecular
electric
4: Direct spin-lattice interactions
3-5: Indirect spin-lattice interaction via electrons
3-6: Chemical shielding and polarization of nuclear spins by
36
2. Tecniche sperimentali
2.4.1
Interazione Zeeman
Per un sistema di spin costituito dal momento magnetico µ l’Hamiltoniana Zeeman imperturbata dovuta alla presenza del campo H0 diretto lungo z è data da:
HZ = −γ~ H0 I.
(36)
Se indichiamo con H1 la perturbazione dovuta all’accoppiamento di µ con il campo H1 (t) =
H1 (cos ωt x − sin ωt y), si ha:
1
H1 = − γ~H1 I+ e−iωt − I− eiωt .
2
(37)
Date le proprietà di I± , H1 ha elementi di matrice non nulli unicamente tra gli autostati di
Iz (imperturbati) |mi e |m + 1i; per questo motivo si indurranno transizioni solo fra livelli
adiacenti, separati da un intervallo di energia ∆E = γ~H0 = ~ω0 . Se si considera il caso
di campi magnetici statici elevati (1÷10 T), l’Hamiltoniana Zeeman risulterà solo perturbata
dalle altre interazioni.
2.4.2
Interazione dipolare diretta
Se i nuclei atomici sono abbastanza vicini, come nel caso dei nuclei di carbonio nei fullereni
(distanza C−C ' 1.4 Å), il contributo dell’accoppiamento dipolare fra di essi alla larghezza
delle transizioni Zeeman è piuttosto significativo. L’interazione di uno spin nucleare con il
campo magnetico degli spin circostanti agisce direttamente attraverso lo spazio, e dipende
dal valore del rapporto giromagnetico γ dei nuclei.
Una stima grossolana del campo dipolare prodotto da un nucleo a distanza r è data da:
Hloc =
µ
.
r3
(38)
Se r=2 Å e µ = 10−3 µN allora Hloc ∼ 1 Gauss.
In modo più rigoroso possiamo rappresentare l’interazione tramite la Hamiltoniana
"
#
X
(µj · rk,j )(µk · rk,j )
1 X µj · µk
Hdip = −
µk Hk,j =
−3
3
5
2
rk,j
rk,j
k,j
(39)
k,j
Come si vede, l’interazione dipende fortemente dalla distanza e dall’orientazione reciproca
degli spin: questo si traduce nella presenza di una parte fortemente anisotropa dell’interazione. Dal momento che Hloc può essere, in modo del tutto casuale, sia parallelo sia antiparallelo
ad H0 , ciò causa un allargamento nella riga di risonanza: il sistema assorbe radiofrequenza
entro una gamma di ±1 Gauss attorno alla risonanza. A tale risultato si perviene anche con
una trattazione quantistica dell’interazione (limitata al primo ordine perturbativo) che può
essere descritta classicamente cosı̀: il dipolo µk precede attorno ad H0 per cui ha una componente statica lungo il campo e una rotante nel piano perpendicolare ad esso. Dal momento
2.4. Interazioni di base in NMR dello stato solido
37
che la componente statica è diversa da spin a spin a seconda dell’inclinazione del singolo
dipolo rispetto all’asse z, questo genererà campi locali diversi in ogni sito, con conseguente
allargamento di riga.
Analizziamo, per semplicità, il caso di due spin I ed S sottoposti ad un campo magnetico
orientato lungo z; i livelli Zeeman imperturbati, nel caso particolare di due spin 1/2, sono
quelli rappresentati in figura 18. Siano θ e φ le coordinate polari ed r il vettore che indica
la loro posizione relativa. È utile scrivere l’hamiltoniana dipolare in una forma che mette
meglio in evidenza gli elementi di matrice della perturbazione:
Hdip =
γI γS ~2
(A + B + C + D + E + F ) ,
r3
(40)
dove
A = Iz Sz (1 − 3 cos2 θ)
1
B = − (I + S − + I − S + )(1 − 3 cos2 θ)
4
3
C = − (I + Sz + Iz S + ) sin θ cos θ e−iφ
2
3
D = − (I − Sz + Iz S − ) sin θ cos θ eiφ
2
3
E = − I + S + sin2 θ e−2iφ
4
3
F = − I − S − sin2 θ e2iφ
4
(41)
L’hamiltoniana completa (HZ +Hdip ) non commuta con l’hamiltoniana Zeeman, (solo il termine A contiene operatori che commutano con l’hamiltoniana Zeeman e, nel caso di una coppia
di spin identici, anche B). I termini che commutano costituiscono la cosiddetta parte secolare
della hamiltoniana e sono quelli che danno contributo al primo ordine perturbativo. Essendo
già diagonalizzabili sulla base degli autostati Zeeman, essi non mischiano i livelli energetici:
gli autovalori vengono modificati, mentre gli autostati no; la soluzione dell’equazione agli autovalori dell’hamiltoniana complessiva è esatta se ci si limita a considerare Hdip ∝ A + B nel
caso di spin identici. In base a questo modello, in un monocristallo, dove è presente una sola
orientazione dei dipoli, si osserva la separazione della riga centrale in un singolo doppietto
Figura 18: Livelli Zeeman di due spin 1/2
38
2. Tecniche sperimentali
Figura 19: A causa del contributo dei termini A e B dell’hamiltoniana dipolare gli autovalori imperturbati vengono modificati in modo tale che le due transizioni a ∆M = ±1, prima
sovrapposte, si separano dando origine a due picchi distiniti.
di picchi (figura 19). Tuttavia, se al monocristallo non si può applicare un modello semplice
a pochi spin interagenti, cioè ci si trova di fronte ad un sistema a molti spin interagenti, il
risultato macroscopico non è più cosı̀ semplice. Con una trattazione di tipo statistico (metodo
dei momenti, [1]) si arriva ad ottenere un allargamento gaussiano della riga di risonanza, a
conferma di quanto anticipato inizialmente con il ragionamento classico riguardo la presenza
di diversi campi locali [31].
I termini C, D, E, F dell’hamiltoniana dipolare, contenendo gli operatori di innalzamento
e abbassamento (combinazioni delle componenti x e y dell’operatore momento angolare ~I),
non commutano mai con l’hamiltoniana Zeeman. Essi, analogamente al campo H1 (t), sono
responsabili delle interazioni fra gli autostati imperturbati, quindi sono i termini che contribuiscono ai rilassamenti: il loro contributo si quantifica estendendo la trattazione matematica
al secondo ordine perturbativo.
Usando la nota formula per le correzioni agli autostati imperturbati [6]:
un = u0n +
X hn0 |Hdip |ni
u0n0 ,
0
E
−
E
n
n
0
(42)
n 6=n
si trova che i nuovi autostati sono combinazioni di quelli imperturbati con pesi diversi che
dipendono dai termini C, D, E, F . In particolare C e D contengono un solo operatore d’innalzamento in ciascun termine additivo, quindi sono responsabili delle transizioni principali
∆M = ±1 (con M = mI + mS ), mentre E ed F ne contengono due, quindi sono responsabili
delle transizioni meno probabili ∆M = ±2 (transizioni normalmente proibite).
La situazione rappresentata in figura 19 si presenta in modo notevolmente diverso nel
caso di un campione di polveri (fermo restando il fatto che si possa applicare il modello a soli
due spin interagenti). Lo spettro ottenuto in questo caso (chiamato doppietto di Pake, figura
20) risente della presenza di tutte le orientazioni possibili dei dipoli.
2.4. Interazioni di base in NMR dello stato solido
39
Figura 20: Doppietto di Pake di due spin 1/2 identici. L’allargamento in frequenza è dovuto alla
dipendenza dall’orientazione della parte secolare della hamiltoniana, 3 cos2 θ −1. I due picchi più
alti corrispondono alle orientazioni di 90◦ , mentre le due spalle più basse corrispondono a θ = 0.
La distanza fra i due picchi, 3/2 DCC (dipolar coupling constant) con DCC= µ0 γi γj ~/4πhr3 i,
si ottiene semplicemente raddoppiando lo shift in frequenza causato del campo dipolare sulla
transizione di uno dei due spin.
Contrariamente a quanto avviene nei solidi, nelle soluzioni la riga si restringe e perde la
forma del doppietto di Pake, perchè il moto caotico delle molecole fa sı̀ che gli spin nucleari
sentano solo una media temporale della parte spaziale dell’interazione h3 cos2 θ − 1i, su tutte
le orientazioni possibili: l’anisotropia dell’interazione viene cosı̀ mediata a zero. Dal momento
che l’interazione dipolare diretta è puramente anisotropa, essa viene completamente mediata
a zero, per cui negli spettri di soluzioni non è osservabile, anche se continua a manifestarsi
nei rilassamenti tramite i termini di secondo ordine.
In modo più compatto si può rappresentare l’interazione dipolare diretta tramite un tensore di rango 2, per tenere in considerazione la non equivalenza delle tre direzioni spaziali,
cioè l’anisotropia dell’interazione:
Hdip =
X
i6=j
b · Ij .
Ii · D
(43)
Un tensore di rango 2 si può scomporre nella somma di un termine scalare (componente
isotropa) e 2 tensori irriducibili a traccia nulla, dei quali il primo antisimmetrico di rango 1
ed il secondo simmetrico di rango 2. Nel caso particolare dell’interazione dipolare, l’unico
termine diverso da zero è il tensore irriducibile simmetrico di rango 2. Questa formulazione
tensoriale si estende a tutte le interazioni fra spin; in particolare si utilizza la rappresentazione
sferica dei tensori, cioè la rappresentazione degli stessi nella base delle armoniche sferiche. In
questa base, i tensori irriducibili di rango n si trasformano come le armoniche sferiche dello
stesso ordine; questo semplifica molto il formalismo utilizzato in calcoli e simulazioni, in cui
spesso si fa uso di rotazioni.
40
2. Tecniche sperimentali
2.4.3
Interazione dipolare indiretta (J-coupling)
L’interazione di J-coupling, detta anche accoppiamento scalare, contrariamente all’accoppiamento dipolare (che è un’interazione diretta fra gli spin), passa attraverso la mediazione dei
legami elettronici. Inoltre il tensore di J-coupling non è a traccia nulla, quindi la sua parte
isotropa causa uno shift del centro della riga di risonanza: questo rende possibile osservare
l’interazione anche in soluzione. La forza dell’interazione dipolare indiretta dipende, oltre
che dal numero di legami chimici intermedi, dalla densità di carica al nucleo, quindi si può
ricondurre principalmente all’interazione di contatto di Fermi. Quest’ultima rappresenta l’accoppiamento diretto fra lo spin nucleare e lo spin degli elettroni più prossimi al nucleo. In
particolare, essendo questo termine proporzionale a |ψ(0)|2 (la probabilità di trovare un elettrone esattamente sul nucleo), ci si aspetta che siano solo gli elettroni di tipo s ad esercitare
un ruolo in questo fenomeno, essendo gli unici elettroni le cui autofunzioni non hanno nodi
ad r=0. L’interazione di contatto di Fermi è il canale di comunicazione principale fra nuclei e legami elettronici, ed essendo intrinsecamente priva di dipendenza spaziale determina
un’interazione complessiva di J-coupling isotropa. Oltre all’interazione di contatto di Fermi,
ci possono essere anche contributi minori all’accoppiamento scalare:
• interazione diretta fra momento orbitale elettronico e momento nucleare: è un’interazione diretta attraverso lo spazio; è analoga ad un’interazione di chemical shielding a
parte il fatto che è un’interazione fra i due momenti magnetici, senza coinvolgimento di
nessun campo esterno.
Spin-Orbit Chemical Shifts
• interazione iperfine fra spin nucleari e spin elettronici: gli elettroni sono fermioni con
electronic spin
spin 1/2, quindi interagiscono, seppurpolarization
debolmente, con gli spin nucleari. Questa interanucl. B
A useful analogy....
NMR
heavy
zione, è di tipo dipolare,
quindi è completamente indipendente
dal termine di contatto
atom A
di Fermi; inoltre, può evidentemente
aggiungere contributi anisotropi all’interazione
Fermi-contact
spin-orbit
complessiva, contributi cheinteraction
non possono essere
in alcun modo legati
all’interazione di
B0
coupling
contatto di Fermi.
Fermi-Contact Spin-Spin Coupling
electronic spin
polarization
NMR
nucl. A
NMR
nucl. B
Fermi-contact
interaction
Fermi-contact
interaction
M. Kaupp, O. L. Malkina, V. G. Malkin, P. Pyykkö Chem. Eur. J. 1998, 4, 118.
Figura 21: Rappresentazione dell’interazione di J-coupling mediata da un solo legame elettronico. Viene messa in evidenza l’interazione di contatto di Fermi che, in questo caso in cui è
presente un solo orbitale di legame, determina l’orientamento antiparallelo dei momenti nucleari.
Sono rappresentati i momenti magnetici di due nuclei con rapporto giromagnetico γ positivo.
2.4. Interazioni di base in NMR dello stato solido
41
La figura 21 mostra la configurazione di minima energia assunta da due nuclei che interagiscono tramite J-coupling attraverso un solo orbitale di legame. È il principio di Pauli a
dettare questa configurazione: gli elettroni in un orbitale devono avere spin antiparalleli, di
conseguenza, risulteranno orientati antiparallelamente anche i momenti magnetici dei due
nuclei atomici.
2.4.4
Interazione di chemical shift
Questo tipo di interazione si manifesta complessivamente in un’azione di schermo del campo
magnetico esterno. Nella materia, il campo locale al nucleo differisce dal campo applicato.
Ogni nucleo, non essendo isolato, sente anche l’effetto dell’interazione fra il suo circondario elettronico ed il campo esterno; questa interazione generalmente comporta un effetto di
schermo tale per cui il campo locale risulta minore del campo applicato. La differenza fra
essi sarà una quantità legata alla suscettività e agli accoppiamenti dominanti nel materiale.
Anche il chemical shift è di natura tensoriale ed è proporzionale al campo esterno:
b · H0 .
Hcs = γ I · σ
(44)
Generalmente si tengono in considerazione solo la parte isotropa (legata alla traccia) e il
tensore simmetrico di rango 2, che produce effetti di rilassamento in NMR di soluzioni, ed
anche shift anisotropi in NMR dello stato solido. Al contrario, la parte antisimmetrica di
rango 1 non produce effetti fisici significativi. La frequenza di risonanza dipende dal campo
magnetico effettivo sentito dal nucleo che è legato anche alle caratteristiche dello schermo
elettronico il quale, a sua volta, dipende dall’intorno chimico. La dipendenza della frequenza
di risonanza di un nucleo nel composto chimico in cui si trova rende la tecnica NMR un
potente strumento analitico (in particolare per l’analisi di composti liquidi), perchè permette
di distinguere nuclei in siti elettronicamente diversi in una molecola e di analizzare il loro
intorno chimico. Il chemical shift isotropo δ è definito come la differenza fra la frequenza
di risonanza del nucleo nel composto e la frequenza dello stesso nucleo isolato (frequenza di
riferimento, νref ) normalizzata per la frequenza di riferimento stessa. Di fatto, tale frequenza
si prende da quella del nucleo in un composto convenzionalmente scelto per il fatto di avere
interazioni iperfini il più possibile trascurabili.
Espressa in parti per milione (ppm), essa diventa:
δ=
ν − νref 6
10 .
νref
(45)
Convenzionalmente si distingue fra chemical shift δ e chemical shielding σ, definendo quest’ultimo in maniera opposta:
σ=
νnucl − ν 6
10 .
νnucl
(46)
42
2. Tecniche sperimentali
dove νnucl rappresenta la frequenza di risonanza del nucleo “svestito” da qualsiasi interazione
con gli elettroni.
Nel caso particolare del C60 solido, gli elettroni coinvolti nell’azione di schermo chimico sono
quelli dell’orbitale molecolare totalmente riempito più esterno, h1u . Tale orbitale, contrariamente al primo orbitale più esterno t1u , non partecipa alla formazione della struttura a bande
del solido f cc, quindi, dal punto di vista cristallografico, h1u non è un orbitale delocalizzato.
Da questo fatto si deduce che il chemical shift, nelle fulleriti, risulta da un accoppiamento
con elettroni a carattere locale.
In ultima analisi, possiamo dire che tutte le interazioni di shielding o anti-shielding risultano da meccanismi d’accoppiamento iperfini fra elettroni e nuclei; tali meccanismi sono
complicati e spesso implicano la presenza di più contributi. In prima approssimazione si può
tuttavia tentare di ricondurre le interazioni di shift ad un’interazione di tipo dipolare diretta
fra momenti magnetici elettronici (o orbitali, nel caso del chemical shift) e momenti magnetici
nucleari. In base a ciò ci si aspetterebbe che la parte anisotropa di un’interazione di shift sia
“ereditata” dall’interazione dipolare, mentre la parte isotropa possa essere sempre ricondotta
all’interazione di contatto di Fermi con gli elettroni degli orbitali in questione.
2.4.5
Interazione di Knight shift
Nei metalli, l’interazione iperfine fra gli elettroni di conduzione, che si polarizzano a causa
del campo esterno H0 , e il momento nucleare, produce un’ulteriore interazione di shift, nota
come Knight shift. Denotando con ωmet la frequenza di risonanza nei metalli e con ωdia la
frequenza di risonanza dello stesso nucleo in isolanti diamagnetici, l’effetto della parte isotropa
dell’interazione consiste nello shift fra le due frequenze di risonanza ∆ω e può raggiungere
valori considerevoli rispetto a ωd (circa 23% nel rame metallico rispetto al rame diamagnetico
nel CuCl). Si ha che:
ωmet = ωdia + ∆ω.
(47)
Anche in questo caso abbiamo a che fare con un’interazione a carattere tensoriale trattabile
in modo analogo al chemical shift (questo naturalmente esiste anche nei metalli, ma è generalmente minore del Knight shift di circa un ordine di grandezza). Il contributo isotropo
dell’interazione si spiega con un accoppiamento iperfine, riguardante elettroni di conduzione
di bande derivate da stati s (privi quindi di momento angolare) per mezzo dell’Hamiltoniana
di contatto:
H=
8π
γe γn ~2 I · S δ(r)
3
(48)
dove δ(r) è la funzione delta di Dirac; inoltre sono stati definiti µe = −γe ~S, µn = −γn ~I,
rispettivamente il momento magnetico di spin elettronico e il momento magnetico nucleare,
2.4. Interazioni di base in NMR dello stato solido
43
r il raggio vettore che congiunge il nucleo all’elettrone. In base all’equazione (48) si deduce
per il Knight shift:
Kiso =
∆H
8π
=
h |ψk (0)|2 iEF χse
H0
3
(49)
dove h |ψk (0)|2 iEF indica il modulo quadro della componente in onda s della funzione d’onda elettronica mediata al livello di Fermi, e χse è la suscettività di Pauli. Come si nota, la
componente isotropa del Knight shift può essere considerata una semplice conseguenza dell’interazione di contatto di Fermi. Inoltre, dato che ∆ω = γ∆H, in base all’equazione (49) si
deduce che:
1. ∆ω è sempre positivo (tranne in casi particolari che non prendiamo in considerazione).
2. ∆ω è indipendente dalla temperatura nella stessa misura in cui lo sono h |ψk (0)|2 iEF e
χse .
3. ∆ω/ω è indipendente dalla frequenza.
4. ∆ω/ω aumenta con la carica nucleare Z in virtù dell’incremento di h |ψk (0)|2 iEF .
Se oltre al termine di contatto (48) si tiene in considerazione anche un accoppiamento dipolare
fra spin nucleari e spin degli elettroni di conduzione di bande originate da stati p, d, ecc, si
ottiene anche il contributo anisotropo del Knight shift, limitato, come nel caso del chemical
shift, al tensore simmetrico a traccia nulla di rango 2. Questo contributo, quando presente, è
molto importante; in campioni policristallini o polveri esso può essere la causa di significativi
cambiamenti nella forma di riga.
In particolare, nelle fulleriti, il Knight shift riguarda gli elettroni dell’orbitale LUMO del
C60 con simmetria t1u . Come spiegato inizialmente, questo orbitale contiene gli elettroni
donati al C60 dai metalli alcalini ed è responsabile della formazione di bande. Tale orbitale
dunque, nelle fulleriti, risulta delocalizzato in tutto il cristallo ed è l’unico orbitale del C60
(a parte quelli superiori vuoti) che risente della simmetria cristallina. È evidente che, per
sua natura, l’interazione di Knight shift non può derivare da orbitali a carattere locale, come
quelli di tipo h1u responsabili del chemical shift. Per questo motivo le due interazioni di shift
manifestano una peculiare differenza nelle fulleriti: mentre, a causa dell’equivalenza di tutti
gli atomi di carbonio, relativamente al circondario elettronico locale, ciascun atomo è soggetto
al medesimo chemical shift, la situazione non è cosı̀ semplice per quanto riguarda il Knight
shift, data la sua sensibilità alle simmetrie cristalline. Esattamente allo stesso modo in cui,
a causa del disordine meroedrico (paragrafo 1.2), esistono nella struttura f cc delle fulleriti
tre siti di carbonio cristallograficamente non equivalenti, ci si deve aspettare che questi 3 siti
non siano equivalenti nemmeno per quanto riguarda il Knight shift. Questo fatto è stato
verificato sperimentalmente in molte fulleriti, fra cui K3 C60 , Rb3 C60 , Rb2 CsC60 [25, 27].
44
2. Tecniche sperimentali
2.5
Apparato sperimentale NMR
Lo spettrometro NMR comprende l’elettronica che gestisce i tempi d’irraggiamento, i ritardi
e gli altri parametri strumentali (attenuazione, sfasamenti, ecc), tali da poter costruire sequenze d’impulsi mirate ad un determinato esperimento.
Questo è uno strumento complesso che gestisce sia la fase di acquisizione che di ricezione in
un tipico esperimento NMR. In figura 22 è mostrato lo schema a blocchi di un tipico apparato sperimentale NMR; sono schematizzati i due stadi di funzionamento dello spettrometro
(trasmissione e ricezione), oltre alla struttura del circuito utilizzato e il magnete che genera
il campo H0 . I comandi necessari per pilotare lo spettrometro si forniscono via software,
tramite il programma di interfaccia relativo allo strumento usato.
Analizziamo brevemente il funzionamento dei principali blocchi dell’apparato, all’interno del
circuito complessivo.
Il magnete
Generalmente si usano magneti superconduttori, ma per campi bassi anche un normale elettromagnete è sufficiente. I magneti superconduttori sono però più stabili; essi sono costituiti
da una bobina di materiale superconduttore che deve essere tenuta a basse temperature in
un bagno di elio liquido opportunamente schermato. La corrente nel solenoide è persistente, dato che non è soggetta ad alcuna resistenza; tuttavia per lunghi periodi di tempo, o
in misure ad alta risoluzione in cui è richiesta una grande sensibilità, è necessario tenere in
considerazione una eventuale lenta diminuzione del campo: il magnete perde energia a causa
della complicata dinamica dei flussoni al suo interno.
La trasmissione
Dall’oscillatore interno allo stadio di trasmissione di uno spettrometro esce un’onda RF (radiofrequenza) di bassa potenza; il gate, comandato da un oscillatore di clock, genera un
segnale di onde quadre che funge da interruttore per il canale RF. Questo è necessario per
rendere il segnale pulsato; il gate e il generatore d’impulsi di clock sono comandati dal computer, permettendo cosı̀ il controllo della lunghezza e dell’alternanza degli impulsi. Il segnale
viene quindi amplificato in potenza ed, in seguito, raggiunge un circuito di disaccoppiamento
chiamato “T magico” (delimitato dalla zona tratteggiata in figura 22). Quest’ultimo è formato da due coppie di diodi e da un cavo detto λ/4 perchè la sua lunghezza corrisponde ad
1/4 della lunghezza d’onda del segnale RF trasmesso nel cavo. La funzione del “T magico”,
in fase di trasmissione, è quella di trasmettere tutto il segnale amplificato ad alta potenza al
circuito della sonda, evitando di mandare il segnale d’eccitazione al preamplificatore situato a
valle del cavo λ/4. Questo si ottiene nel seguente modo: la prima coppia di diodi rappresenta
2.5. Apparato sperimentale NMR
45
Figura 22: Schema a blocchi dell’apparato NMR
un pezzo di cavo normale per il segnale ad alta potenza proveniente dall’amplificatore, dal
momento che il segnale si trova al di sopra della tensione di soglia; il segnale dunque passa
quasi indisturbato attraverso di essa, mentre la seconda coppia di diodi, essendo riferita a
massa, genera un nodo in quel punto del circuito (la tensione di soglia, 0.5 V, è praticamente
zero rispetto ad un segnale cosı̀ intenso). All’interno del cavo λ/4, essendoci un punto vincolato ad un valore fisso di tensione, si forma un sistema di onde stazionarie in cui λ/4 è la
distanza che separa un nodo di tensione dal primo massimo successivo. Dunque, se l’estremità
del cavo in cui c’è la seconda coppia di diodi rappresenta un nodo di tensione, l’estremità
opposta rappresenta il massimo e questo permette a tutto il segnale in trasmissione di entrare
nel circuito della sonda senza perdite per riflessione. A questo punto, se la sonda è stata ben
accordata tramite sintonizzazione e adattamento d’impedenza, la potenza trasmessa viene
46
2. Tecniche sperimentali
convogliata quasi esclusivamente sulla bobina che avvolge il campione, generando per induzione un campo H1 (t) senza apprezzabili segnali riflessi.
La sonda
La buona qualità o addirittura la riuscita di una misura NMR è notevolmete subordinata
alle caratteristiche del circuito della sonda: è quest’ultimo che crea le condizioni per la risonanza e che, soprattutto, deve essere in grado di minimizzare, in ricezione, i segnali spurii
di disturbo come, ad esempio, quelli prodotti dal comportamento meccanico della bobina in
cui risiede il campione (“ringing”). Le sonde per la risonanza magnetica nucleare possono
essere di diversa concezione, a seconda delle frequenze a cui devono funzionare e del tipo di
campione che si vuole misurare. In generale è utile avere un valore alto del fattore di qualità
Q, anche se è necessario valutare sperimentalmente caso per caso quali siano i parametri circuitali da migliorare; tipicamente può essere necessario abbassare Q anzichè alzarlo, se si ha a
che fare con un “ringing” molto intenso. Il circuito di base delle sonde NMR è rappresentato
in figura 23: le due componenti variabili servono sia per adattare l’impedenza della sonda
a quella del circuito (matching), che per accordare il circuito alla frequenza di risonanza
voluta. Una volta ottenuto l’adattamento d’impedenza con l’induttanza variabile, in modo
da far passare nel circuito una buona parte della potenza trasmessa, si procede a trovare
la frequenza di risonanza azionando il condensatore (tuning). In realtà sorgono complicazioni sperimentali, in quanto i due parametri sono correlati; tutti i componenti circuitali si
influenzano a vicenda e non si può trattare il sistema come se fosse un semplice circuito RLC.
Figura 23: Schematizzazione del circuito di una sonda NMR
La ricezione
In seguito all’eccitazione, nella sonda vengono generati, oltre al segnale di risposta nucleare
atteso, segnali spurii che non hanno nulla a che fare con il campione studiato. Ad esempio,
la risposta meccanica della bobina di eccitazione induce su di essa un segnale di “ringing”
alla frequenza di risonanza che, nei primi istanti successivi alla fine dell’impulso, può coprire
2.5. Apparato sperimentale NMR
47
completamente il segnale NMR. Questo infatti è un segnale molto debole che non supera la
tensione di soglia dei diodi. Questo è il motivo per cui il comportamento del “T magico” in
ricezione è del tutto diverso da quello in trasmissione: il segnale NMR è a tensione cosı̀ bassa
che vede le coppie di diodi come circuiti aperti, quindi non si può dirigere verso lo stadio
di trasmissione dello spettrometro, ma solo verso quello di ricezione. Dopo essere passato
attraverso il preamplificatore, che serve anche da adattatore d’impedenza, il segnale entra
nel miscelatore e qui viene miscelato con due segnali di riferimento alla stessa frequenza,
(coerenti perchè provenienti dallo stesso oscillatore). Miscelare un segnale complesso con un
altro ad una frequenza quasi uguale o simile, serve per abbassare la frequenza del segnale in
uscita rendendola cosı̀ facilmente campionabile; ripetere questa procedura due volte con due
segnali di riferimento sfasati è una tecnica chiamata quadratura. In questo modo, si ottengono
due segnali a bassa frequenza in uscita dal mixer che ci permettono di ricostruire sia la
parte dissipativa del segnale, che presenta un massimo alla frequenza di risonanza e che sarà
associata al segnale “reale”, sia la parte dispersiva associata invece al segnale “immaginario”.
In realtà, i segnali acquisiti sono in genere una combinazione lineare del segnale dissipativo
e dispersivo, ma in sede di analisi possono essere opportunamente combinati per riassumere
il significato attribuitogli sopra. Infine, i segnali vengono filtrati, amplificati e digitalizzati
prima di giungere al buffer del PC.
48
2. Tecniche sperimentali
Capitolo 3
Misure e risultati
Il lavoro sperimentale ha riguardato, in primo luogo, la caratterizzazione magnetica dei campioni di K3 C60 . In base alle misure di magnetizzazione effettuate su questi campioni, è stata
accertata la presenza di una differenza di suscettibilità di Pauli χP fra i campioni costituiti
da un’abbondanza naturale di
13 C
effettuate anche misure NMR sul
e quelli arricchiti all’85%. Successivamente sono state
13 C,
al fine di misurare la suscettibilità dall’interazione di
Knight shift.
Per la caratterizzazione magnetometrica dei campioni di K3 C60 , ci siamo avvalsi di misure
effettuate con il magnetometro SQUID (superconducting quantum interference device) situato
presso l’istituto IMEM CNR di Parma, in collaborazione con il Dr. F. Bolzoni.
Le misure NMR di
13 C
sono state effettuate presso il Dipartimento di Fisica e al centro
interfacoltà misure (CIM) del nostro ateneo, con la collaborazione del Dr. C. Vignali.
3.1
Misure di magnetizzazione
Nelle fulleriti supercondutive sono presenti diversi tipi di risposte agli stimoli magnetici, aventi ordini di grandezza spesso confrontabili; la magnetizzazione misurata sperimentalmente
rappresenta dunque il risultato complessivo di diversi contributi, di cui è necessario tenere
conto se si vuole ricavare il valore della sola suscettibilità di Pauli. Le curve sperimentali di
M = M (T ) sono come quelle riportate in figura 24, dove sono distinguibili, in primo luogo,
3 contributi alla magnetizzazione:
1. Contributo di Curie, dovuto alle impurezze paramagnetiche (spesso presenti nelle fulleriti).
2. Contributo diamagnetico della fase superconduttiva al di sotto di Tc ;
3. Contributo costante indipendente dalla temperatura: questo termine è direttamente
correlato alla risposta magnetica degli elettroni metallici, ritenuta costante in tempe49
50
3. Misure e risultati
Figura 24: Curva di magnetizzazione di una generica fullerite superconduttiva. Nel grafico a
sinistra la linea continua rappresenta il contributo di Curie, mentre quella tratteggiata rappresenta
il contributo, costante in temperatura, rimanente dopo la sottrazione del termine di Curie. A
sinistra è graficata la dipendenza dal campo applicato del contributo costante in temperatura
della magnetizzazione.
ratura; oltre alla suscettibilità di Pauli comprende i termini di core, il diamagnetismo
di Landau ed il contributo delle impurezze ferromagnetiche.
Il termine di Curie, dovuto alle impurezze paramagnetiche, è stato fittato con la prevista
dipendenza da T χp ∼
C
T,
e, successivamente, sottratto in modo da ottenere una precisa
valutazione del contributo costante in temperatura. [25].
Quest’ultimo è stato determinato a diversi valori del campo applicato. La dipendenza dal
campo riscontrata è mostrata in figura 24; come si vede, essa è lineare solo per valori alti del
campo. La deviazione dall’andamento lineare trovata per campi minori di 1.5 T si attribuisce
alla presenza di impurezze ferromagnetiche; in un materiale ferromagnetico infatti la magnetizzazione aumenta col campo fino ad arrivare ad un valore di saturazione. Per questo motivo
l’effetto di questo tipo di impurezze diventa semplicemente un termine additivo al di sopra
di 1.5 T, dove l’andamento è perfettamente lineare. Questo suggerisce che il valore corretto
della suscettibilità di Pauli si ottenga dalla pendenza della retta in figura 24 ad alti campi,
dove le impurezze ferromagnetiche non contribuiscono più alla pendenza della retta.
A questo punto è necessario prendere in considerazione la presenza di ulteriori contributi
alla suscettibilità, costanti in temperatura, che dunque non sono distinguibili, solo in base
all’analisi descritta, dal termine di Pauli. È significativa la risposta magnetica degli elettroni
orbitali (elettroni di core); la suscettibilià di core, che per il C60 neutro e gli ioni di potassio
risulta rispettivamente χcore = −260 · 10−6 emu/mole e χcore = −14.6 · 10−6 emu/mole [17], è
a sua volta costituita da due contributi, il primo diamagnetico, dovuto alle shell elettroniche
interne ed il secondo debolmente paramagnetico dovuto alla rimozione della degenerazione
fra gli orbitali π più esterni da parte del campo magnetico (paramagnetismo di Van Vleck).
51
3.1. Misure di magnetizzazione
M(T) in K3C60
−4
x 10
0
Max. magn. Field: 2Oe
Magnetic Moment [emu]
−2
FC
−4
−6
−8
−10
ZFC
−12
−14
10
15
20
25
30
Temperature [K]
Figura 25: Misura SQUID della magnetizzazione del K3 C60 in funzione della temperatura. La
curva più in alto è stata misurata durante il raffreddamento in campo del campione (field cooling);
l’altra, contrariamente, deriva da una misura effettuata durante il riscaldamento del campione a
partire dallo stato superconduttivo ottenuto in campo nullo. Ciò che differenzia le due curve è la
dinamica irreversibile dei flussoni, presente in superconduttori di secondo tipo come le fulleriti.
Entrambe le curve si congiungono alla temperatura critica del K3 C60 , Tc = 19.2 K.
M(T) in K3C60
−3
2
x 10
Magnetic Moment [emu]
0
Increasing magn. Field
−2
Max. magn. Field: 2Oe
−4
−6
−8
−10
5
10
15
20
25
30
35
40
45
50
55
Temperature [K]
Figura 26: Set di misure SQUID ripetute a diversi campi applicati. Graficando la parte costante
della magnetizzazione in funzione del campo, si ottiene ad alti campi un andamento lineare come
da figura 24.
52
3. Misure e risultati
Dal momento che le shell elettroniche interne non vengono modificate dalla struttura cristallina, il contributo diamagnetico rimane sostanzialmente invariato anche nel C3−
60 presente
nelle fulleriti di tipo A3 C60 , in cui il metallo alcalino dona 3 elettroni al C60 . Al contrario, è
difficile determinare il contributo del paramagnetismo di Van Vleck. Quest’ultimo è dovuto al
fatto che il campo esterno determina una sovrapposizione degli autostati del sistema separati
in energia; cosı̀ il momento angolare orbitale, normalmente soppresso dal campo cristallino,
emerge di nuovo determinando una debole risposta paramagnetica.
In generale questo contributo dipende dal tipo di fullerite considerata, dunque il valore di
χcore riportato, relativo alla molecola neutra, può essere diverso nel caso del K3 C60 ; tuttavia,
sebbene questo porti ad un errore sistematico nella valutazione del valore finale di χp , non
compromette il confronto dei valori ottenuti per lo stesso composto, in cui il contributo di
Van Vleck è necessariamente il medesimo. Infine, ricordo che alla suscettibilità magnetica
complessiva contribuisce anche il termine di Landau, dovuto alla suscettibilità orbitale degli
elettroni liberi (χLandau ); tuttavia sembra ragionevole l’ipotesi che nelle fulleriti questo contributo sia trascurabile a causa del corto cammino libero medio degli elettroni: quest’ultimo
non sarebbe tale da determinare un’orbita sufficientemente ampia affinchè questo termine sia
confrontabile con i precedenti.
In ogni caso, analogamente a quanto affermato per il paramagnetismo di Van Vleck, la
presenza di errori sistematici nel valore finale di χp , eventualmente dovuti anche al termine di
Landau, non compromette il confronto dei risultati ottenuti fra campioni di K3 C60 costituiti
da una abbondanza naturale di
13 C
e campioni arricchiti, dal momento che la struttura
elettronica è la medesima.
Le curve sperimentali seguono l’andamento riportato in figura 24; la misura è stata eseguita con due metodologie diverse: raffreddamento in campo nullo (ZFC, zero field cooling)
e raffreddamento in campo (FC, field cooling) [4]. Nel primo caso, rappresentato in figura
25 dalla curva che raggiunge i valori più bassi di magnetizzazione, durante il raffreddamento
non è presente la dinamica irreversibile dei flussoni, quindi la frazione diamagnetica ottenuta
è maggiore. La misura è effettuata a partire dalle più basse temperature riscaldando via via
il campione. La curva superiore è ottenuta raffreddando il campione già immerso nel campo;
come si vede la dinamica dei flussoni impedisce al campione di avere una risposta altrettanto
diamagnetica come nel caso precedente.
I valori misurati della suscettibilità di Pauli per il K3 C60 sono elencati nella tabella 4;
le prime misure sono state effettuate su una serie di campioni sintetizzati con lo stesso metodo, uno dei quali costituito da una percentuale naturale di
13 C
(UN), mentre i rimanenti
due arricchiti all’85% (UP, UK). Successivamente, le misure sono state ripetute per un altro
campione non arricchito, sintetizzato in un secondo tempo con un metodo differente (ZH).
Il motivo di questo cambiamento nella sintesi dei campioni deriva dal fatto che, in seguito alle
53
3.1. Misure di magnetizzazione
Campioni
Suscettibilità (10−3 emu/g T)
UN
UP
UK
ZH
5.408
4.48
4.02
6.35
percentuale di
13 C
1.07 %
85 %
85 %
1.07 %
Tabella 4: Suscettibilità di Pauli misurata nei campioni di K3 C60 .
misure NMR sul carbonio, è stata riscontrata nella prima serie di campioni una percentuale
consistente di C60 non reagito. Le misure magnetometriche dei primi campioni ci forniscono
quindi una sottostima della suscettibilità di Pauli, dal momento che il C60 non ha elettroni
metallici, e dunque non contribuisce al paramagnetismo di Pauli. È stato tuttavia possibile
stimare la percentuale di C60 non reagito presente in ciascun campione con misure NMR, in
modo da rinormalizzare i valori sperimentali di χp al peso effettivo del K3 C60 . Basandoci solo
sui dati non rinormalizzati, possiamo comunque già notare che la suscettibilità dei campioni
arricchiti risulta sistematicamente più bassa di quella del campione in cui è presente una
abbondanza naturale di
13 C.
Come è ragionevole pensare in base alle analoghe condizioni di
Figura 27: Magnetizzazione in funzione del campo per il K3 C60 . Viene mostrata la curva su cui
giacciono i valori della parte costante in temperatura della magnetizzazione, a cui è stato già
sottratto il contributo di Curie delle impurezze paramagnetiche; risulta evidente come, per bassi
campi, la linearità si perda a causa delle impurezze ferromagnetiche, la cui magnetizzazione non
è ancora saturata.
54
3. Misure e risultati
sintesi dei campioni in questione, in ciascuno di loro dovrebbe essere presente approssimativamente la stessa quantità di C60 non reagito. In questo caso il risultato della rinormalizzazione
in peso sarà semplicemente quello di aumentare proporzionalmente i valori misurati, lasciando sempre quelli dei due campioni arricchiti minori dell’altro. Ci si aspetta che il valore
rinormalizzato del campione con abbondanza naturale, coincida col valore di suscettibilità
misurato nell’ultimo campione di K3 C60 sintetizzato, esente dal difetto di sintesi dei primi.
Questo confermerebbe la presenza di un effetto isotopico, ma non l’andamento previsto dal
modello nonadiabatico, secondo il quale l’aumento della massa isotopica determinerebbe un
aumento della suscettibilità di Pauli. Nella figura 27 è mostrata la dipendenza della parte
costante della suscettibilità in funzione del campo, per il campione di K3 C60 sintetizzato
correttamente; la successiva analisi NMR del
13 C
ha confermato la coincidenza fra i valori di
χp dei due campioni non arricchiti.
3.2
Misure NMR
La strumentazione utilizzata è la seguente:
• Gli spettrometri Stelar e Tecmag, usati nel range di frequenze di 25÷95 MHz per il 13 C.
• Gli amplificatori di potenza AMT (American Microwave Technology, 6÷220 MHz, 300 W),
ENI (10÷86 MHz, 1 kW), Kalmus ( 10÷270 MHz, 1 kW).
• I criomagneti superconduttori Oxford BZH 200/89 da 4.7 T e Cryomagnetics da 9 T.
Il primo è stato utilizzato inizialmente ad un valore di campo intermedio, successivamente è stato portato fino al valore massimo del campo; questo magnete, rispetto al
Cryomagnetics, possiede una migliore omogeneità di campo essendo dotato di bobine
correttive (shim coils).
• Il magnete superconduttore Oxford (400 MHz per 1 H, 9.5 T), situato al CIM (Centro Interfacoltà Misure), dotato di sonda ad alta risoluzione (< 1 ppm) associata allo
spettrometro Bruker AMX 400. Questo spettrometro è stato utilizzato ad ulteriore
conferma degli spettri NMR di
13 C
dei campioni arricchiti (UK e UP).
• Criostato Oxford CF 1200, utilizzato per misure a bassa temperatura su
13 C.
• Sonda Bruker associata al magnete Oxford 200 MHz e sonda criogenica costruita appositamente per il criostato Oxford CF 1200.
55
3.2. Misure NMR
Figura 28: Il magnete superconduttore Cryomagnetics da 9 T e lo spettrometro Apollo. A fianco
è rappresentata l’immagine schematica della struttura interna di un magnete superconduttore.
Figura 29: Struttura interna di un magnete superconduttore.
56
3. Misure e risultati
3.2.1
NMR su
13
C
Data l’esiguità degli effetti isotopici è di fondamentale importanza che le misure NMR sul
13 C
siano effettuate in un campo magnetico il più possibile omogeneo; l’allargamento delle
righe dovuto alla disomogeneità del campo potrebbe infatti “ricoprire” eventuali spostamenti
delle righe stesse e quindi rendere difficile la valutazione sia del contributo isotropo delle
interazioni di shift, sia della parte anisotropa, per valutare la quale è necessaria una analisi
della forma di riga intrinseca.
Sono state dunque effettuate alcune misure preliminari per stabilire la massima omogeneità di campo; in seguito, si è proceduto alla misura a temperatura ambiente dei campioni
arricchiti. La forma di riga è costituita da due picchi ben distinti; questo risultato era del
tutto inatteso, dal momento che la riga di risonanza del K3 C60 , a temperatura ambiente,
doveva essere semplicemente una singola curva centrata sulla frequenza di risonanza, senza
alcuna sottostruttura.
A temperatura ambiente gli spettri NMR delle fulleriti presentano caratteristiche tipiche
degli spettri di campioni liquidi: per quanto siano composti cristallini la rotazione caotica
dei fullereni rende tutti i nuclei di
13 C
equivalenti dando luogo ad una singola riga; inoltre
media a zero le interazioni anisotrope presenti, restringendo la riga (motional narrowing).
Confrontando questa misura effettuata in un campo di 3.78 T con altre a campi differenti,
13
C NMR spectrum of K C
3 60
0.15
Temperature: 290 K
Frequency: 40.482 MHz
Sample: UP (85% 13C)
Intensity [arb. units]
41.7 ppm
0.1
FWHM: 20 ppm
FWHM: 16 ppm
0.05
0
−100
−50
0
50
100
150
Frequency [ppm]
Figura 30: Spettro NMR di 13 C, a temperatura ambiente, del K3 C60 in un campione arricchito
all’85% di 13 C. In picco più basso è stato identificato come un residuo di C60 non reagito ancora
presente nel campione.
57
3.2. Misure NMR
è risultato subito evidente che la distanza in ppm fra i due picchi rimaneva invariata. Questo,
inizialmente, porta a pensare che la presenza di due picchi può essere dovuta a qualche interazione proporzionale al campo. In effetti è cosı̀; infatti successivamente abbiamo verificato
che il picco meno intenso non era relativo al K3 C60 , ma era dovuto ad una percentuale di C60
puro, ancora presente nel campione.
La presenza di questa frazione è da attribuire ad una parziale reazione del C60 con l’azide
di potassio nella formazione di K3 C60 , lo spettro NMR risultava viziato dalla presenza del
picco a frequenza inferiore, nella stessa posizione del picco di C60 puro, come ci si è resi conto
in misure successive effettuate a parità di condizioni sperimentali (figura 31).
13
C NMR spectrum of K C
3 60
and C
Temperature: 290 K
0.8
samples: 85% 13C
0.7
Intensity [arb. units]
60
Frequency: 50.324
0.6
C60
0.5
K3C60
0.4
0.3
0.2
0.1
0
−200
−150
−100
−50
0
50
Frequency [ppm]
100
150
Figura 31: Spettri NMR di 13 C del C60 puro e del K3 C60 in campioni arricchiti all’85% di 13 C.
Il confronto rende evidente che nello spettro del K3 C60 è presente un picco di C60 non reagito.
La separazione fra i due picchi, in seguito al motional narrowing, non è altro che la parte isotropa del Knight shift del K3 C60 e come tale determina un aumento della frequenza
di risonanza proporzionale al campo applicato (vedi paragrafo 2.4.5). Si può dunque effettuare una prima valutazione dell’influenza che l’arricchimento isotopico ha sul Knight shift
osservando eventuali cambiamenti della sua componente isotropa fra i campioni con diversa
abbondanza isotopica di
13 C.
In particolare il K3 C60 con abbondanza naturale di
13 C
ma-
nifesta un Knight shift isotropo pari a 44 ppm, maggiore di circa 2 ppm del valore ottenuto
nei campioni arricchiti (vedi figura 30). Questo conferma quanto precedentemente dedotto
dalle misure SQUID: l’aumento della massa isotopica dei campioni causa una diminuzione
della polarizzazione indotta nei nuclei dalla risposta magnetica degli elettroni di conduzione,
58
3. Misure e risultati
Figura 32: Spettri NMR di 13 C a temperatura ambiente: (a) polvere di C60 puro; (b) Kx C60
con x ∼ 1.5; (c) Kx C60 con x ∼ 2; Kx C60 con x ∼ 3.1.
quindi una diminuzione della suscettibilità di Pauli.
Il difetto stechiometrico di potassio è stato determinato dal tipo di metodologia usata
inizialmente nella sintesi dei campioni. Dopo aver compresso insieme, per mezzo di un pastigliatore, le polveri di C60 con quelle di azide di potassio, (KN3 ) nelle adeguate proporzioni,
la pastiglia ottenuta veniva sottoposta ad un trattamento termico durante il quale le azidi si
decomponevano secondo la reazione:
3 KN3 + C60 −→ K3 C60 +
9
N2 .
2
(50)
Una volta liberato l’azoto gassoso, il potassio è libero di diffondere nei siti interstiziali del
C60 cristallino. Questo processo avviene durante l’annealing a 430◦ prolungato per 1 giorno.
Il difetto stechiometrico del potassio è probabilmente dovuto ad una parziale evaporazione
di quest’ultimo durante la decomposizione delle azidi che è un processo rapido e fortemente
esotermico, dunque è ragionevole pensare che una simile transizione di fase possa provocare
anche l’evaporazione di una certa quantità di potassio. Come risultato, nel campione finale
di K3 C60 , si è presentata la situazione descritta in figura 32 (c).
Questo problema è stato risolto successivamente utilizzando un altro metodo di sintesi che si basa sul drogaggio diretto del C60 .
In primo luogo si sintetizza del K6 C60
ponendo direttamente il C60 puro in annealing insieme al potassio metallico in quantità
sovrabbondante.
È da premettere che il motivo per cui non si usa direttamente la quantità di potassio
stechiometricamente corretta per ottenere del K3 C60 , è che non è possibile pesare il potassio
59
3.2. Misure NMR
metallico in modo preciso. Dato che 6 è il numero massimo di ioni alcalini intercalabili nei
siti interstiziali delle fulleriti, è evidente che la misura corretta della quantità di potassio
è irrilevante per la sintesi di K6 C60 . Una volta ottenuto questo, si ripete il trattamento
termico, aggiungendo al campione di K6 C60 la quantità di C60 necessaria ad ottenere un
numero doppio di moli di K3 C60 . Il trattamento termico avviene alla temperatura di 350◦ C
per un periodo di sette giorni; il K3 C60 è il composto più stabile della famiglia, dunque la
sua formazine è favorita perchè porta ad una diminuzione di energia libera. In questo modo
è stato sintetizzato un primo campione di K3 C60 puro con un’abbondanza naturale di
13 C.
Come precedentemente anticipato, abbiamo rinormalizzato al peso effettivo del K3 C60 i
valori della suscettibilità misurata sui primi campioni. Questo è stato effettuato utilizzando
una stima della quantità di C60 non reagito, ottenuta dal calcolo delle aree sottese dai due
picchi riscontrati nelle misure. Questa correzione dovrebbe essere valida a prescindere dal tipo
di conformazione che il C60 non reagito assume all’interno dei campioni; tuttavia sono state
effettuate, preliminarmente, misure di recupero di inversione della magnetizzazione (inversion
recovery) al fine di avere una idea qualitativa della distribuzione del C60 nei campioni.
3.2.2
Determinazione dei tempi di rilassamento spin-reticolo
Le misure di inversion recovery ci permettono di determinare il tempo di rilassamento spinreticolo T1 di un materiale (vedi paragrafo 2.3.2). Nel caso specifico dei campioni di K3 C60 in
difetto di potassio, questo ci permette di caratterizzare i due picchi studiati. Ci si aspetta che
il C60 puro, arricchito all’85%, abbia un tempo di rilassamento di 10 s, decisamente superiore
a quello del K3 C60 , risultato essere solo 0.33 s.
Queste misure sono state effettuate su campioni arricchiti; il rapido rilassamento del
K3 C60 è infatti principalmente dovuto al Knight shift, che è presente in entrambi i tipi di
campione, dunque non ci si aspetta un grande cambiamento di T1 al variare dell’abbondanza
isotopica di
13 C.
La situazione è completamente diversa per il C60 solido, in cui il fattore
limitante del rilassamento è l’interazione dipolare. La scomparsa di quest’ultima al diminuire
dell’abbondanza isotopica di
13 C,
passando dal C60 arricchito a quello normale, determina
un aumento di T1 da 10 a 50 secondi. Per motivi di carattere sperimentale, si è preferito
effettuare le misure di inversion recovery sui campioni arricchiti in cui il C60 solido ha un
tempo di rilassamento minore.
I risultati dei fit sulle misure sono mostrati nelle figure 33, 34, 35; il valore di T1 ricavato
per C60 non reagito è decisamente inaspettato. Si ottiene infatti un tempo di rilassamento
T1 = 0.43 s, sicuramente maggiore del tempo di rilassamento del K3 C60 , ma sempre molto
minore del valore tipico del C60 puro, T1 = 10 s.
60
3. Misure e risultati
Measurement of T on K C
1
3 60
1.5
Normalized Intensity
1
0.5
Single exponential fit
T1=0.331±0.0093 Sec
Amp1=1.94±0.026
0
Offs=−0.915±0.0079
Temp.=290 K
−0.5
−1
0
0.5
1
1.5
Time [seconds]
Residues
0.1
0
−0.1 −3
10
−2
10
−1
10
0
1
10
10
Figura 33: Stima del tempo di rilassamento T1 nel K3 C60 (campione UP).
Measurement of T1 on C60
1.5
Normalized Intensity
1
0.5
Single exponential fit
T1=10±0.079 Sec
0
Amp1=1.92±0.0073
Offs=−0.92±0.0074
Temp.=290 K
−0.5
−1
0
10
20
30
Time [seconds]
40
50
Residues
0.05
0
−0.05 −2
10
−1
10
0
10
1
10
2
10
Figura 34: Stima del tempo di rilassamento T1 nel C60 puro arricchito all’85% di
13
C.
3.2. Misure NMR
61
Figura 35: Stima del tempo di rilassamento T1 del picco di C60 non reagito nel K3 C60 . È
evidente che, anche se la stima è resa imprecisa dalla difficoltà di escludere il picco di K3 C60 ,
dalla routine di fitting dei dati, questo picco rilassa molto più velocemente del C60 puro.
Abbiamo interpretato questo risultato ritenendo che il C60 non reagito non sia segregato,
ma diffuso in piccoli cluster, in modo approssimativamente omogeneo, per tutto il campione:
in queste condizioni, i monocristalli di C60 , privi di una struttura di bulk, risultano fortemente
influenzati dal circondario. Si può pensare che il comportamento del C60 non reagito sia
dettato da “effetti di superficie”, il cui risultato complessivo è quello di assimilare il tempo
di rilassamento del C60 a quello del K3 C60 .
3.2.3
Rinormalizzazione in peso della suscettibilità
Il peso effettivo del K3 C60 nei campioni sintetizzati con le azidi di potassio è stato valutato
a partire dalle aree sottese dai picchi di C60 e di K3 C60 . Attraverso programmi di fitting
dei dati,è stato possibile determinare con una buona precisione il rapporto fra le aree. Tale
rapporto non è uguale in tutti i campioni, ma si aggira attorno a 0.20/0.25.
I valori rinormalizzati della suscettibilità di Pauli per i vari campioni sono riportati in
tabella 5. Le percentuali di C60 non reagito non sono cosı̀ diverse fra i vari campioni, soprattutto fra quelli arricchiti, da causare un effetto molto disomogeneo; di conseguenza, i valori
62
3. Misure e risultati
Figura 36: Risultato dell’analisi dei picchi per il campione UP. Il fit è reso difficoltoso per la
presenza di spalle leggermente irregolari ai piedi dei due picchi; in questo caso si ha comunque
un risultato soddisfacente. il rapporto fra le aree dei due picchi è ∼0.223.
di χP auli subiscono più che altro un generico innalzamento, secondo quanto ci si aspettava.
Ora si nota che i due valori di suscettibilità relativi ai due campioni non arricchiti sono quasi
identici; i rimanenti due differiscono maggiormente fra loro, tuttavia rimangono sistematicamente minori dei precedenti; questo conferma la presenza dell’effetto isotopico cercato.
Campioni
χP auli (10−3 emu/g T)
C60 non reagito
arricchimento
UN
UP
UK
ZH
6.42
5.34
5.02
6.35
17.88%
18.23%
22.63%
0%
1.07%
85%
85%
1.07%
Tabella 5: Suscettibilità di Pauli nei campioni di K3 C60 , rinormalizzata in base al peso effettivo
del K3 C60 presente.
3.2.4
Analisi della forma di riga in funzione della temperatura
È evidente che prima di fare ulteriori considerazioni sulle misure di suscettibilità, è necessario
disporre anche di un campione di K3 C60 puro, arricchito all’85% di 13 C, su cui rifare le misure
SQUID. Sui campioni arricchiti presenti, sono state effettuate anche misure NMR su
13 C
a
bassa temperatura, in modo da bloccare i residui moti uniassiali delle molecole (paragrafo 1.2)
3.2. Misure NMR
63
e fare emergere le caratteristiche anisotrope delle interazioni presenti nel composto. Questa
analisi in temperatura è stata effettuata al fine di simulare, successivamente, la forma di riga
NMR del
13 C
in condiziomi statiche. Le misure (riportate in figura 37) sono state effettuate
con lo spettrometro Stelar ad un campo di 2.4 T. Quello che ci si propone di ottenere è
una buona valutazione dell’effetto del Knight shift anisotropo e dell’interazione dipolare, che,
essendo un tensore a traccia nulla, non si può vedere a temperatura ambiente a causa del
motional narrowing. La componente isotropa di Knight shift, al contrario, è diversa da zero,
quindi è già visibile a temperatura ambiente ed è evidentemente responsabile dello shift verso
le alte frequenze del picco di K3 C60 rispetto al C60 puro (41.7 ppm). È importante notare che
la misura a 5 K in figura 37 è ampiamente al di sotto della temperatura di transizione allo
stato superconduttivo, che per il K3 C60 è Tc =19.2 K; per quanto riguarda le considerazioni
sugli shift anisotropi e l’interazione dipolare, ci si deve riferire alle righe NMR relative a
temperature superiori a Tc . Questo si deduce dal fatto che le interazioni di cui si è parlato
riguardano l’influenza reciproca fra nuclei ed elettroni: la dinamica di questi ultimi viene
radicalmente modificata dalla transizione allo stato superconduttore. Al di sotto di Tc la
formazione delle coppie di Cooper svuota la banda di conduzione dagli elettroni, dunque non
si può più parlare di Knight shift o di suscettibilità di Pauli come risposta magnetica degli
elettroni liberi.
La forma di riga a bassa temperatura al di sopra di 20 K non è facilmente interpretabile;
certamente le spalle laterali asimmetriche sono di natura dipolare, mentre non appare evidente
l’effetto delle interazioni anisotrope di shift sulla forma di riga. Per capire in che misura
competono queste interazioni alla formazione dello spettro, è necessario procedere ad una
simulazione numerica della forma di riga.
64
3. Misure e risultati
13
C NMR spectra of K3C60 vs. temperature
Enriched 13C sample UP
Spect. Freq. = 25.855 MHz
T = 284 K
5
T = 240 K
T = 200 K
Amplitude (arb. units)
4
T = 150 K
T = 90 K
3
T = 70 K
T = 40 K
2
T = 30 K
1
T = 20 K
T=5K
0
−2
−1.5
−1
−0.5
0
0.5
1
1.5
2
4
Frequency (Hz)
x 10
Figura 37: Spettri NMR di K3 C60 in funzione della temperatura. Al di sopra di 90 K il picco
stretto del C60 non reagito spunta ancora sopra le spalle larghe che sorgono all’abbassarsi della
temperatura. Al contrario il picco stretto di K3 C60 scompare molto prima perchè i fullereni nel
K3 C60 non sono altrettanto liberi di ruotare come nel C60 puro: i moti rotazionali del K3 C60
vengono bloccati molto prima.
Capitolo 4
Simulazioni della forma di riga
NMR
Le simulazioni numeriche hanno un ruolo molto importante in NMR dello stato solido, dove si
è costretti ad interpretare i dati sperimentali utilizzando modelli semplificati che comprendono
solo pochi spin. Il confronto fra dati sperimentali e i risultati delle simulazioni basate sul
sistema di spin semplificato è necessario per capire in che misura le interazioni presenti
concorrono alla formazione dello spettro NMR. Questo approccio è quello usato anche in
questo caso allo scopo di identificare il contributo di Knight shift anisotropo nella forma di
riga del K3 C60 .
4.1
Modello semplificato del sistema di spin
Le interazioni NMR dominanti nei cristalli molecolari di fullereni sono le interazioni di shift
chimico e l’interazione dipolare diretta; nel caso di sistemi metallici, come il K3 C60 , è molto
significativo anche il Knight shift, dovuto alla risposta degli elettroni di conduzione al campo
esterno. Le interazioni quadrupolari non sono invece presenti, essendo il carbonio privo di
momento di quadrupolo. Notiamo subito che la struttura f cc del cristallo molecolare può
essere completamente ignorata per quanto riguarda l’identificazione di un modello semplificato di sistema di spin. Lo scopo di tale modello è essenzialmente quello di ottenere la
migliore approssimazione del circondario elettronico di un generico nucleo di
13 C
del C60 e
quindi delle interazioni a cui esso è soggetto. Dal momento che la distanza minima fra 2
nuclei di
due
13 C
13 C
situati in fullereni diversi (∼ 3.7 Å) è mediamente molto maggiore di quella fra
adiacenti nella stessa molecola (1.45 Å), l’interazione dipolare nel primo caso risulta
molto minore che nel secondo, e dunque trascurabile (Hdip ∝ 1/r3 , vedi paragrafo 2.4.2). Il
contributo dell’interazione dipolare fra nuclei appartenenti a molecole diverse si tiene semplicemente in considerazione introducendo un allargamento gaussiano della riga NMR simulata.
65
66
4. Simulazioni della forma di riga NMR
Considerazioni analoghe valgono per il chemical shift, essendo quest’ultimo dovuto ad un’azione degli elettroni locali (vedi paragrafo 2.4.4). Solamente il Knight shift è influenzato dalla
struttura cristallina per i motivi spiegati nel paragrafo 2.4.5; tuttavia questo si schematizza
nella presenza di 3 siti di
13 C
non equivalenti, e ciò si tiene in considerazione semplicemente
ripetendo la simulazione in ciascun caso e sommando infine i risultati con gli opportuni pesi.
In linea di principio, il sistema di spin da considerare potrebbe essere già una singola
molecola di C60 ; tuttavia con 60 spin, avendo a che fare con interazioni tensoriali, il calcolo
numerico risulta improponibile data la dimensione delle matrici coinvolte. Il modello semplificato che verrà utilizzato nel nostro caso si limita ai soli 3 primi vicini al nucleo di
13 C
considerato rappresentativo. In base a quanto detto sulla struttura del C60 nel paragrafo 1.1,
questo sistema di spin è costituito dai 4 spin centrali della struttura formata da 2 esagoni e 1
pentagono in figura 38. Già in questo caso semplice di soli 4 spin la formulazione operatoriale
del sistema porta ad uno spazio di Hilbert a 16 dimensioni ( 12 ⊗ 12 ⊗ 12 ⊗
1
2
= H16 ), dunque a
matrici 16×16.
Figura 38: Sistema di 4 spin che rappresenta il modello semplice usato nelle simulazioni. Il
nucleo centrale, colorato di rosso, è quello rappresentativo di un generico 13 C del K3 C60 , dunque
il solo spin da osservare nella acquisizione NMR simulata.
4.2
Formulazione teorica
L’evoluzione temporale del sistema di 4 spin sotto l’azione degli impulso RF si tratta nel quadro della meccanica statistica quantistica, utilizzando il formalismo della matrice di densità
σ [6, 19], che rappresenta la generalizzazione quantistica dell’ordinaria funzione di distribuzione ρ di insiemi statistici classici. In statistica classica la funzione di distribuzione ρ(q, p)
fornisce immediatamente la distribuzione delle probabilità dei diversi valori delle coordinate
e degli impulsi delle particelle del sistema. In statistica quantistica, invece, non è cosı̀: gli
67
4.2. Formulazione teorica
elementi di matrice di σ danno solo la probabilità di trovare il sistema in uno o in un altro
stato quantistico, senza nessuna indicazione concreta circa i valori delle coordinate o degli
impulsi delle particelle.
In virtù della natura stessa della meccanica quantistica, la statistica basata su di essa può
solo trattare il problema della ricerca delle distribuzioni di probabilità per le coordinate e gli
impulsi separatamente, non contemporaneamente, a causa del principio di indeterminazione.
Essenzialmente, le distribuzioni di probabilità richieste devono tener conto sia della indeterminazione statistica che della indeterminazione intrinseca della descrizione quantistica come
tale.
4.2.1
Rappresentazione degli operatori di spin
Gli operatori di spin si scrivono, come di consueto, nella forma di rappresentazione matriciale
sulla base degli autostati Zeeman. Nel caso di spin
1/2, alle matrici di Pauli.
!
0 1/2
Ix =
, Iy =
1/2 0
0
−i/2
i/2
0
!
1
2
essi coincidono, a meno di un fattore
, Iz =
1/2
0
0
−1/2
!
.
(51)
Dal momento che il problema va formulato nello spazio di Hilbert complessivo di tutti gli
spin, è necessario costruire operatori di spin che abbiano la dimensionalità dell’intero spazio.
Il modo più immediato di fare ciò è valutare il prodotto diretto degli operatori di spin nei
singoli sottospazi; ad esempio, in un sistema a 3 spin di numeri quantici 12 , 1, 12 , si ottiene:
∗ =I ⊗I ⊗I
I1x
1x
2
3

..
.


MATRICE

∗
I1x
=

12 × 12


..
.



=


0
1/2
1/2
0
!

1 0 0



⊗
⊗
0
1
0


0 0 1
1 0
0 1
!
. (52)
Come si vede le dimensioni delle matrici risultanti crescono notevolmente all’aumentare del
numero di spin; per sistemi con N spin
1
2
si ha una dimensionalità pari a 2N .
Sebbene sia più intuitivo rappresentare gli operatori di spin nella base degli autostati
Zeeman, essi si possono rappresentare in qualsiasi altra base; in particolare conviene utilizzare la rappresentazione nella base dei tensori sferici irriducibili [21], quando si ha a che
fare con calcoli che implicano rotazioni, come nel nostro caso, in cui si vuole simulare uno
spettro di polveri. L’algoritmo che calcola la media da polveri è il processo che appesantisce
maggiormente il calcolo nelle nostre simulazioni. Esso procede ad una scansione su tutte le
orientazioni possibili dei dipoli rispetto al campo magnetico: la singola acquisizione NMR
viene ripetuta dopo ogni piccola rotazione del sistema; da qui emerge l’importanza di un
formalismo che semplifichi il calcolo degli operatori di spin sotto rotazione.
68
4. Simulazioni della forma di riga NMR
4.2.2
Hamiltoniana del sistema di spin
L’Hamiltoniana completa del sistema di spin è:
H = HZ + Hdip + HCshif t + HKshif t ,
X
X
X
X
b · H0 ,
b · Ij +
b · H0 +
γ Ii · σ
Ii · K
Ii · D
H =
−γ~ Ii · H0 +
i
i
i6=j
(53)
i
b σ
b sono tensori di rango 2.
b, K
dove D,
Se consideriamo ogni interazione singolarmente, la relativa Hamiltoniana può essere equivalentemente espressa in termini di tensori sferici irriducibili:
HINT =
l
X X
l
(−1)m A l,−m T l,m ,
(54)
m=−l
dove A l,−m , e T l,m sono rispettivamente gli elementi dei tensori spaziali e dei tensori di spin
relativi all’interazione considerata. Ogni generico tensore di rango 2 può essere rappresentato in termini delle sue tre componenti irriducibili. La prima è semplicemente uno scalare
corrispondente alla traccia del tensore, e quindi alla parte isotropa dell’interazione che esso
rappresenta, le altre sono entrambe tensori a traccia nulla, il primo dei quali antisimmetrico
di rango 1 ed il secondo simmetrico di rango 2. Possiamo quindi scrivere:


Axx Axy Axz


b =  Ayx Ayy Ayz  =
A


Azx Azy Azz
RANGO 0




RANGO 1
Aiso
0
0
0
Aiso
0
0
0
Aiso


0
αxy


 +  −αxy
0


−αxz −αyz
RANGO 2
αxz


δxx δxy δxz



αyz 
 +  δxy
0
δxz
δyy
δyz


(55)
δyz 

δzz
,
dove
1
b ,
Aiso = T r{A}
3
1
αxy = (Axy − Ayx ) ,
2
1
δxy = (Axy + Ayx − 2Aiso ) .
2
Tenendo presente ciò, in base a considerazioni di simmetria sulle interazioni coinvolte, è possibile effettuare alcune semplificazioni: l’interazione dipolare non possiede una parte isotropa
ed è ovviamente simmetrica per la sua stessa natura. Inoltre, secondariamente, si nota che
essa è invariante per rotazione attorno all’asse congiungente i due spin. Ne risulta che l’interazione dipolare si può rappresentare matematicamente con un tensore simmetrico, a traccia
nulla e cilindrico, cioè tale che δxx = δyy nel sistema di assi cartesiani in cui l’asse z coincide
b coincide
con la congiungente dei due spin (PAS, Principal axis system). Dunque il tensore D
69
4.2. Formulazione teorica
( −2
β
µ 0γ 1 γ 2 h
)
4π r123
zz
D
xx
l
D
(α , β , γ )
m
m′m
β e 2iγ
D
yy
µ2
r12
µ1
s 2 β − 1)
2β e
D
iγ
Figura 39: Rappresentazione grafica del tensore dipolare nel sistema degli assi principali: si
tratta di un ellissoide i cui assi hanno una lunghezza proporzionale agli elementi diagonali del
tensore.
3
1
δ
(3cos 2 β − 1)
3 I I 2 z − I1 I 2
con la sua componente irriducibile
simmetrica di rango 2; 1i zrelativi
tensori spaziali, in un
8
6
sistema di assi cartesiani generico, assumono la forma:
1
2
1
=
bβ − 1) 3I1 z I 2 z − I1 I 2
A0 0 =δ (3cos
− √ T r{D}
3
2
H = A20T20 =
A1 0
= A1±1 = 0
3
A2 0Figure
= 3.5√The
Dhomonuclear
dipolar interaction in the rotating frame
zz
6
A2±1 = ∓(Dxz ± iDyz )
1
A2±2 =
(Dxx − Dyy ± 2iDxy ) = ±2iDxy .
2
(56)
Di questi solo il temine A2 0 è diverso da zero nel sistema degli assi principali.
Analoghe considerazioni valgono per le interazioni di shift, con l’unica differenza che esse
hanno una componente isotropa diversa da zero, dunque A0 0 risulterà diverso da zero. In
ogni caso i termini non diagonali dei tensori spaziali sarebbero trascurabili. Gli esperimenti
NMR di cui effettuiamo le simulazioni sono nella condizione di alto campo, dunque hanno
importanza solo i termini della Hamiltoniana che commutano con la Hamiltoniana Zeeman,
mentre si trascura l’effetto dei termini perturbativi. L’equazione (54) si potrebbe dunque
riscrivere in modo molto più semplice:
HINT =
X
A l,0 T l,0 .
(57)
l
Si deduce che, nelle simulazioni, è stato sufficiente costruire l’Hamiltoniana complessiva solo
con i termini l = 0, ed l = 2.
70
4. Simulazioni della forma di riga NMR
4.2.3
Evoluzione temporale e acquisizione
La matrice di densità in condizioni di equilibrio è data da:
σeq =
1 −h H/kT
e
,
Z
(58)
dove H è l’Hamiltoniana del sistema e Z la funzione di partizione.
L’assunzione ~ H/kT → 0 è generalmente soddisfatta in esperimenti NMR, quindi si può
sviluppare l’esponenziale,
σeq ∝ 1 −
hH
.
kT
(59)
Inoltre in condizioni di alto campo l’operatore identità può essere ignorato e H ∼ HZ ; dunque
la matrice di densità ridotta, nel caso semplice di un solo tipo di nucleo, assume la forma:
σeq = Fz ,
dove Fz =
P
i Iz .
(60)
Nel caso di sistemi eteronucleari, al contrario, le temperature di spin devono
essere esplicitamente considerate.
Avendo costruito la matrice di densità iniziale σ(0), l’evoluzione temporale di quest’ultima
in assenza di rilassamento è data dalla nota equazione di Liouville-Von-Neumann:
i
dσ(t)
= [ H , σ(t) ] ,
dt
(61)
che ha per soluzione
σ(t) = U (t, 0) σ(0) U (t, 0)† ,
(62)
dove U (t, 0) è l’operatore evoluzione temporale dal tempo 0 al tempo t:
U (t, 0) = e−2πi H t .
(63)
La presenza del fattore 2π all’esponente è necessaria se si utilizza la convenzione di esprimere
l’Hamiltoniana in unità di frequenza
L’impulso RF non è stato preso in considerazione nella costruzione della Hamiltoniana del
sistema, in quanto l’impulso non è presente durante la fase di acquisizione del FID, nella quale
σ evolve secondo H. Inoltre, per tutta la durata dell’impulso, si può trascurare l’evoluzione
di σ secondo l’Hamiltoniana rappresentata dall’equazione (53), in quanto l’irraggiamento RF
domina sulle altre interazioni. Dunque l’effetto della radiofrequenza può essere considerato
come un impulso deltiforme che semplicemente ruota la matrice densità iniziale attorno ad
un certo asse. Ad esempio un impulso di fase φ = 0 e durata τ tale che ω1 τ = π/2 ruota σ di
90◦ attorno ad x. Sempre nel caso di sistemi omonucleari, l’operatore evoluzione, per questo
impulso è:
U (π/2) = e iπ Fx /2 .
(64)
4.3. Descrizione del programma
71
Ciò che interessa ai fini dell’acquisizione è l’evoluzione temporale di σ successiva alla fine
dell’impulso di eccitazione. Essa è rappresentata dalla soluzione dell’equazione (61) con la
condizione iniziale σ(0) = U (π/2) σeq U (π/2)† (utilizziamo un impulso di 90◦ per semplicità).
L’equazione che indica come i valori d’aspettazione delle osservabili cambiano nel tempo è:
hAi = T r{A σ(t)} .
(65)
Il FID simulato sarà dato dall’evoluzione temporale dei valori d’aspettazione di una osservabile che simula un’acquisizione in quadratura. Tale osservabile è l’operatore d’innalzamento
I + (o analogamente l’operatore d’abbassamento; gli spettri finali sono equivalenti a meno di
diverse correzioni di fase).
4.3
Descrizione del programma
La simulazione di un esperimento di risonanza per mezzo di linguaggi di programmazione
di basso livello richiederebbe uno sforzo notevole nella scrittura del codice, il quale, inoltre,
risulterebbe poco esportabile e di difficile lettura; in questi linguaggi, infatti, non sono definiti
dei tipi di dato adatti a riprodurre il comportamento degli oggetti matematici precedentemente descritti. Di conseguenza, nel nostro caso, il programma è stato scritto in C++ e fa
riferimento a GAMMA (http://gamma.magnet.fsu.edu), una libreria di C++ creata allo scopo
di semplificare le simulazioni dei fenomeni di risonanza: essa permette di scrivere semplici
programmi strutturati che utilizzano il formalismo astratto.
4.3.1
GAMMA C++ library
GAMMA (General Approach to M agnetic resonance M athematical Analysis) semplifica la
scrittura del programma finale, dal momento che è una libreria programmata ad oggetti. La
programmazione ad oggetti è un approccio innovativo alla scrittura del codice particolarmente
versatile nel C++ nel quale sono sviluppate caratteristiche come l’incapsulamento dei dati
e l’overloading delle funzioni. All’interno di GAMMA vengono definiti dei nuovi tipi di dati,
quali operatori, tensori, ecc. Essi sono costruiti in perfetta analogia con i tipi di dati standard
presenti nella maggior parte dei linguaggi, come il C (integer, floating). Ogni tipo di dato
costituisce una classe, un oggetto astratto che rende accessibili alle funzioni esterne solo le
informazioni relative al modo con cui deve interfacciarsi con esse (incapsulamento). Se, ad
esempio, si tratta di un oggetto matematico, tali informazioni sono quelle relative alla sua
manipolazione algebrica. Questa struttura permette di scrivere le simulazioni finali con dei
semplici programmi strutturati basati sul formalismo astratto descritto nel paragrafo 4.2; ciò
è possibile perchè il codice finale invoca i tipi di dati definiti in GAMMA, esattamente come
se fossero tipi di dati standard. Inoltre il codice di GAMMA è già stato compilato prima
72
4. Simulazioni della forma di riga NMR
Figura 40: Rappresentazione dei vari livelli a cui si può affrontare la scrittura del codice.
dell’esecuzione della simulazione, e questo fatto aumenta sensibilmente l’efficienza di calcolo
nel caso di esperimenti su sistemi a più spin.
4.3.2
Simulazione di esperimenti NMR
Il problema della simulazione di una riga NMR può essere affrontato con due approcci
differenti:
1. Simulazione diretta dello spettro finale nello spazio delle frequenze.
2. Simulazione del FID nello spazio dei tempi; in questo caso lo spettro è dato dalla
trasformata di Fourier del FID simulato, che può essere analizzato come se fosse il
risultato di una reale acquisizione NMR.
Nel primo caso si considera ogni singola transizione j → k come una funzione deltiforme
centrata a ωj,k e di ampiezza Aj,k . GAMMA, al contrario, è stata scritta pensando ad un
approccio di secondo tipo; dunque le simulazioni effettuate sul K3 C60 sono strutturate in modo
4.3. Descrizione del programma
73
Figura 41: Struttura di una singola acquisizione NMR
da riprodurre effettivamente la dinamica di una acquisizione NMR. Il programma restituisce in
output una serie di n valori che rappresentano l’evoluzione temporale dei valori d’aspettazione
di I + , calcolati secondo l’equazione (65). Tali valori, inseriti in un grafico ampiezza-tempo,
rappresentano il free induction decay (FID). Il problema consiste essenzialmente nel simulare
la dinamica NMR di un sistema di spin in condizioni statiche (da confrontare con le misure sul
K3 C60 effettuate a bassa temperatura dove tutti i moti rotazionali sono congelati); dunque,
una volta definita l’Hamiltoniana H in forma sferica irriducibile, come descritto nel paragrafo
4.2.2, e l’intervallo di tempo fra due campionamenti successivi, il segnale può essere calcolato
semplicemente dall’evoluzione della matrice di densità iniziale secondo l’operatore U (t, 0) =
e−2πi H t . L’impulso RF si considera ideale e viene trattato secondo quanto descritto nel
paragrafo 4.2.3.
Nella figura 41 sono elencati i passaggi fondamentali della simulazione di una singola acquisizione NMR. Dal momento che i campioni di K3 C60 sono costituiti da polveri, per ottenere
uno spettro realistico, si utilizza un algoritmo che ripete più volte la struttura riportata in
figura 41 variando di volta in volta l’orientazione del sistema rispetto al campo magnetico. In
questo modo si simula la presenza di tanti monocristalli ciascuno dei quali orientato in modo
diverso rispetto al campo, e quindi dotato, a causa dell’anisotropia delle interazioni presenti,
di un diverso set di autovalori Zeeman; questo determina una distribuzione in frequenza delle
transizioni Zeeman. Tale processo, definito media da polveri, è ciò che appesantisce maggiormente il calcolo in una simulazione NMR. Il formalismo dei tensori sferici irriducibili serve
74
4. Simulazioni della forma di riga NMR
proprio per rendere più agile la rotazione del sistema di spin effettuata all’interno dell’algoritmo di media da polveri. Tutte le simulazioni sono state effettuate su un computer con
processore AMD Athlon XP 1800+ con 516 Mb di RAM, dotato un sistema operativo Red
Hat Linux release 7.2. Esse hanno richiesto tempi differenti a seconda del tipo di interazioni
considerate e della sensibilità angolare dell’algoritmo di media da polveri.
4.3.3
Struttura delle simulazioni in GAMMA
Il nostro programma inizia con la definizione del sistema di quattro spin descritto nel paragrafo 4.1. A tale scopo si fa uso della classe dynamic spin system che è la classe più completa
fra quelle usate da GAMMA per rappresentare il sistema fisico di partenza (vedi figura 42).
Definendo un sistema di spin di questo tipo, si possono inserire anche le coordinate dei nuclei,
b nel
da cui vengono calcolati i tensori dipolari, e i parametri che definiscono un tensore A,
sistema principale degli assi Aiso , δzz e η = (δxx − δyy )/δzz .
Figura 42: Classi che definiscono il sistema di spin in GAMMA.
Ad esclusione dell’algoritmo di media da polveri che può essere implementato in vari
modi al fine di migliorare l’efficienza della simulazione, il modo in cui è strutturata una
singola acquisizione viene ottimizzato nell’utilizzo delle funzioni della classe Acquire. Per
mezzo di esse è possibile rendere il codice ancora più compatto riducendo al minimo anche la
formulazione analitica, come si vede nella figura 41 che riassume la struttura di una singola
acquisizione NMR. Il programma inoltre fa uso delle classi spin T e space T , con le quali
si costruisce l’Hamiltoniana in forma sferica irriducibile nella condizione di alti campi (vedi
l’eq. (57)). Le relazioni che legano le componenti irriducibili di un generico tensore spaziale
For an irreducible rank 1 spatial tensor the spherical and Cartesian components are inter-related by
1
1
− ------ [ A x ± iA y ] = −
A 1, ±1 = +
+ ------- A ±
2
2
A 1, 0 = A z
GAMMA
Dipole-Dipole Interactions
1
4.3. Descrizione
programma
- [ – A 1, 1 + A 1,Example
= -----A x del
Programs
–1 ]
2
(19-6)
i
A y = ------- [ A 1, 1 + A 1, –1 ]
2
102
3.7
75
For a general rank 2 spatial tensor the irreducible spherical components can also be expressed in
di rango 2 alle sue componenti cartesiane sono le seguenti:
terms
the Cartesian
components. In this case the following equations apply.
Theofresult
is
–h 21γ γ 2 ±l
–1
- [i A-j xx + A yy +mA zz ] = -----A 0, D0 = -----D - Tr { A }
H i, j = ------------(
–
1
)
D
(
ij
)T
(6)
lm
l –3m ( ij )
3r 3 ∑ ∑
ij
l=0 m
–i
–1
A 1, ±1 = ------ [ ( A zx – A xz ) ± i ( A zy – A yz ) ]
A 1, 0 = ------- [ A xy – A yx ]
2
2
3.19.8 Dipole-Dipole
Spherical Tensor Spin Components
1
We can thus obtain the 9 irreducible
spherical components 1of the dipolar spin tensor (rank 2),
A , 0 = ------- [ – A xx – A yy + 2 A zz ] = ------- [ 3 A zz – Tr { A } ]
TlD– m ( ij ) , directly2from
the 6
Cartesian components, 〈v|T̂ij |u〉6, as indicated in GAMMA Class Documentation on Spin Tensors. The nomenclature used here for a tensor component is
1
1
A 2, ± 1 = −
+ --- [ ( A xz + A zx ) ± i ( A yz + A zy ) ]T l, m , A 2, ±2 = --- [ ( A xx – A yy ) ± i ( A xy + A yx ) ]
2
2
(19-7)
theequations,
subscript l spans
thethe
rank
(in this case
2) as l = [0,are
2],expressed
and the subscript
m spans
l, m
Thewhere
inverse
where
Cartesian
components
relative
to the+/spherical
com=
[-l,
l].
The
nine
formulas
for
these
quantities
a
listed
in
the
following
figure.
Perponents,
quantoare
riguarda,
invece, i tensori
di spin, nel caso di un’interazione fra spin come quella
readily verifiable
as the following.
Spherical
Spin Tensor Components
GAMMA
Shift Anisotropy
Interactions
145
dipolare,
abbiamo:Dipolar Irreducible
Example Programs
3.7
–1
1
D
T 0, 0 ( ij ) = ------- I iz Ijz + --- ( Ii+ Ij- + Ii- I j+ )
2
3
3.15.8 Shift Anisotropy Spherical Tensor Spin Components
–1
–1 D
D
--------T1,the
= ---------- [ Ii+spherical
I j- + Ii- I j+components
]
T 1of
( ij )CS= rank
[ Ii± I jz + I iz I j ±1 ]
0 ( ij9)irreducible
, ±1the
We can obtain
2 2 CS
2 22 “spin” tensor directly from
the Cartesian components, 〈v|T̂ |u〉 , as indicated in GAMMA Class Documentation on Spin Tensor. These are
1
D
T 2, 0 ( ij ) = ------- [ 3I iz I jz – ( I i • I j ) ]
6
T lCS
,m,
1
D
1
D
T 2, ± 2 ( ij ) = --- [ I i± I j ± ]
T2, ± 1 (the
ij ) chemical
= −
I jz + Iiz Ij interaction.
]
+ --- [ I i± shielding
where CS signifies
The
tensor
index
±
2l spans the rank:
2
l ∈ [ 0, 2 ] while the tensor index m spans l : m ∈ [ – l, l ] The nine formulas for these quantities
Scott
Smith
May 20, 1998
a listed
in the
figure
where
field components
areinteraction.
those of the normalized field vector
Figure
3-3following
The rank
2 spin
tensorthe
components
for a dipolar
2
Se si BThe
ha
che fare con interazioni fra gli spin e il campo esterno come il Knight shift e il
n. a
matrix representation of these nine tensor components will depend upon the matrix represen1. These in turn depend
tations
of the
individual
operators
from
which
they
are constructed
chemical
shift,
i tensori
dispin
assumono
la
forma:
Shielding
Rank
2spin
Irreducible
Spherical
Spin-Space
Tensor
Components
upon the spin quantum numbers of the two spins involved. For a treatment of two spin 1/2 particles
the dipolar tensor components are– 1expressed1in their matrix form –(spanning
the composite Hilbert
1= ------- product
I z B z + ---basis
( I + Bof
+GAMMA
I - B+ ) =as-----I • B n2 (spin indices implicit).
space of the two spins) inTthe
follows
0, 0 default
2
3
3
–1
T 1, 0 ( i ) = ---------- [ I + B- – I - B + ]
2 2
–1
T 1, ±1 ( i ) = ------ [ I ± Bz – I z B± ]
2
1
T 2, 0 = ------- [ 3I z Bz – ( I • B n ) ]
1. Note that the spin tensors are invariably constructed
6 in the laboratory coordinate system. Here the z-axis corresponds to the direction of the spectrometer static magnetic field and the coordinate system is right-handed.
2. The GAMMA program1DipSpinT.cc on page 118 generated these matrices. 1
---
− --- [ I B + I B ]
T 2, ± 1 = +
2 ± + z z ±
T 2, ± 2 =
2
[ I± B± ]
Scott Smith
August 24, 1999
For a spin 1/2 particle and B = B B , the matrix form of these tensor components are shown in
0 n come la coppia di spin, il programma ha dato buoni
In seguito
a test su sistemi 0semplici
the following figure in the single spin Hilbert space. The spin index has been omitted, the field
components
are those of
normalized
Bn .
risultati,
riproducendo
in the
modo
esattovector
il doppietto
di Pake. In questo caso l’algoritmo di
The
representation
nine
tensor components
depend
upon
the matrixirepresenmedia
damatrix
polveri
utilizzato ofè these
molto
semplice:
il raggiowill
vettore
che
congiunge
due spin (di
tations of the individual spin operators from which they are constructed3. These in turn depend
cui uno
posto
nell’origine
degli
assi)
esegueFor
una
scansione
nelle coordinate
uponè the
quantum
number of
the spin
involved.
a treatment
of aangolare
spin 1/2 particle
the shieldingpolari
tensor
components
are expressed
in their
matrix
form
in thecon
default
of GAMMA
as
(θ, φ),
in cui
la sensibilità
angolare
in φ
viene
pesata
unproduct
fattorebasis
sin θ.
Di conseguenza
si attribuisce un peso maggiore alle orientazioni aventi θ = 90◦ rispetto a quelle con θ = 0◦
1. Due to the nature of the CS interaction, the rank 2 tensor treatment produces a “spin” tensor
CS
T l, m which
contains spatial components, namely the magnetic field vector. As a result, care must be used when performing spatial rotations on shielding tensors. Any spatial rotations must involve rotations of both σ and T
2. For these formulae, it is important to note that it is the second component in the composite spin/space tensor
which is set to the normalized magnetic field vector B n , although we might just as well have used the first
vector instead. The difference is that the l = 1 equations would then appear of opposite sign from those given
76
4. Simulazioni della forma di riga NMR
in modo da esplorare uniformemente tutto l’angolo solido. In un secondo tempo, sempre
utilizzando questo semplice modello di media da polveri, sono stati simulati gli spettri dovuti
alle sole interazioni di shift.
Chemical shift + Knight shift simulated
for the three inequivalent carbon sites C1, C2, C3
4
x 10
C1 shift = 164 + ( −4, −25, 29 )
4
x 10
C2 shift = 177 + ( 0, −33, 33 )
4.5
5
freq. 25.855 MHz
4
freq. 25.855 MHz
3.5
4
3
3
2.5
2
2
1.5
1
1
0.5
0
0
2000
4000
6000
8000
2000
4000
Hz
6000
8000
Hz
average shift = 185 + ( −28, −61, 89 )
C3 shift = 197 + ( −47, −80, 127 )
4
x 10
18000
2.5
16000
freq. 25.855 MHz
freq. 25.855 MHz
2
14000
12000
1.5
10000
8000
1
6000
4000
0.5
2000
0
2000
4000
6000
Hz
8000
2000
4000
6000
8000
Hz
Figura 43: Simulazioni delle interazioni di shift per i 3 siti di carbonio cristallograficamente non
equivalenti. In ciascun caso il calcolo è stato effettuato con una sensibilità angolare di 1◦ ha
richiesto solo pochi minuti.
77
4.4. Simulazioni delle sole interazioni di shift
4.4
Simulazioni delle sole interazioni di shift
È noto che per le simmetrie del gruppo spaziale a cui appartiene, la struttura del K3 C60 può
essere costruita a partire da tre siti di carbonio cristallograficamente non equivalenti; come già
anticipato, (vedi paragrafo 2.4.5) a questi tre nuclei di carbonio corrisponde quindi un diverso
Knight shift. In base a calcoli sulla struttura a bande, si vede che i tre siti non equivalenti
hanno una densità di stati al livello di Fermi che, per il K3 C60 , scala con un rapporto pari a 12
: 7 : 4. Si assume che la forma del tensore di Knight shift sia la stessa per i tre siti di carbonio,
e che i tensori scalino fra loro con lo stesso rapporto che c’è fra le densità degli stati. Questa
assunzione è ragionevole se si pensa che gli orbitali π circostanti non sono molto diversi,
l’unica diversità è quella della densità di stati determinata dalla struttura a bande. Risulta
quindi possibile determinare i tre tensori sulla sola base di tre parametri Kiso , Kxx = Kyy ,
Kzz . Conoscendo il valore medio del Knight shift per il K3 C60 costituito da un’abbondanza
naturale di
13 C,
(Kiso = 37 ppm, Kxx = Kyy = −86 ppm, Kzz = 172 ppm) [25], sono stati
ricavati i differenti tensori relativi ai tre siti di
13 C
non equivalenti C1 , C2 , C3 :
C1 −→ 49 + (−114 −114 228) ppm
b =
K
C2 −→ 29 +
(−67
−67
134) ppm
C3 −→ 16 +
(−38
−38
76)
ppm
Sommando questi valori a quelli del Chemical shift, uguale per tutti i
13 C
(σiso = 148 ppm,
σxx = 34 ppm, σyy = 67 ppm, σzz = −101 ppm), sono stati ottenuti i tensori di shift complessivi per il K3 C60 . Su di essi si basano le simulazioni mostrate in figura 43 . Successivamente
è stata implementata una versione del programma iniziale che ripete la simulazione per tre
volte utilizzando un tensore totale con una componente di Knight shift diversa ogni volta,
per poi sommare proporzionalmente i tre spettri in output.
4.5
Simulazioni della sola interazione dipolare
Ai fini della simulazione delle sole interazioni di shift non interessa la struttura del sistema di
spin usato, in quanto le interazioni hanno origine dall’interazione del singolo spin con il campo
esterno; al contrario, nel caso dell’interazione dipolare (∝ 1/r3 ), la struttura del sistema di
spin gioca un ruolo fondamentale, in quanto determina il circondario dipolare dello spin
rappresentativo. Nel nostro caso specifico, la modellizzazione del C60 , descritta nel paragrafo
4.1, corrisponde ad approssimare il circondario dipolare ai soli primi vicini. Di conseguenza,
come è mostrato in figura 44, è stato considerato un sistema a 4 spin dove si prendono in
considerazione solo le interazioni dipolari con lo spin centrale, considerato rappresentativo di
tutti i carboni della molecola di C60 .
78
4. Simulazioni della forma di riga NMR
Figura 44: Circondario dipolare del carbonio rappresentativo in centro. Le linee gialle rappresentano le interazioni dipolari presenti fra gli spin; quelle che non riguardano lo spin centrale
sono escluse dalla hamiltoniana dipolare.
Nella generalizzazione delle simulazioni dipolari di una singola coppia di spin al nostro
sistema di spin, è stato necessario implementare una versione più complessa dell’algoritmo
di media da polveri. In base alle misure effettuate a bassa temperatura, ci si aspetta che il
contributo dipolare alla forma di riga sia molto evidente, più intenso delle interazioni di shift,
alla frequenza a cui sono state effettuate le simulazioni (25.855 MHz).
In figura 45 è mostrato il risultato di una prima simulazione preliminare del contributo
dipolare alla forma di riga. La larghezza di riga corrisponde a quella misurata sperimentalmente, le spalle dipolari sono ben visibili, ma la caratteristica più evidente dello spettro è la
simmetria rispetto all’asse delle ordinate. Questo ci permette di attribuire direttamente alle
interazioni di shift le eventuali asimmetrie presenti nelle simulazioni finali.
Figura 45: Simulazione preliminare dello spettro da polvere dipolare; il calcolo ha richiesto circa
2 ore.
4.6. Simulazioni comprensive di interazione dipolare, chemical e Knight shift
4.6
79
Simulazioni comprensive di interazione dipolare, chemical
e Knight shift
I campioni di K3 C60 misurati sono isotopicamente arricchiti in
13 C
all’85%. È necessario
tenere conto di questo fatto anche nel modello semplificato di quattro spin. Effettuando
su di esso un calcolo statistico, si ottiene che nel 61% dei casi tutti i 4 nuclei sono di
mentre nel 32.5% solo tre nuclei su quattro sono di
13 C;
13 C,
la rimanente percentuale, pari a
6.5%, comprende tutti gli altri casi.
È evidente che, al fine di valutare correttamente il contributo dipolare alla forma di riga,
non si può trascurare il caso in cui uno dei tre nuclei attorno al carbonio rappresentativo sia
di
12 C,
dal momento che questa situazione si presenta con una probabilità del 32.5%.
In figura 46 sono messe a confronto la forma di riga del K3 C60 arricchito all’85% di
Figura 46: Confronto fra Spettro del K3 C60 a 30 K e una prima simulazione comprensiva di
tutte le interazioni. Si vede che la larghezza dello spettro simulato è sostanzialmente corretta;
in entrambi i casi la presenza dei due picchi laterali è evidente; l’asimmetria delle spalle laterali è
certamente dovuta alle interazioni di shift. Si nota subito che essa è molto più accentuata nella
simulazione; se tale caratteristica dovesse essere sistematicamente confermata in simulazioni
successive, allora potrebbe essere imputata ad una differenza di Knight shift anisotropo fra
campioni con differente abbondanza isotopica. La simulazione ha richiesto circa 2 ore.
13 C
80
4. Simulazioni della forma di riga NMR
misurata a 30 K, ed il risultato di una prima simulazione preliminare comprensiva di tutte le
interazioni presenti. In essa si tiene conto sia della presenza dei tre tensori di Knight shift
differenti, sia della presenza della percentuale non trascurabile di
12 C.
Il FID ottenuto da GAMMA è stato moltiplicato per un fattore gaussiano, in modo
da ottenere nello spettro un corrispondente allargamento. In questo modo si tiene conto
dell’effetto medio di allargamento della riga, dovuto all’accoppiamento dipolare dello spin
rappresentativo con tutti gli altri nuclei della molecola, e in secondo luogo, del cristallo. In
un sistema a molti spin infatti, non è possibile dedurre lo spettro da modelli semplici (vedi
paragrafo 2.4.2); il numero di transizioni possibili è cosı̀ elevato che si deve approssimare
l’interazione effettiva ad una media.
Utilizzando questa approssimazione, detta metodo dei momenti [1], si conclude che l’effetto complessivo dell’interazione dipolare su questi sistemi è proprio un allargamento gaussiano
omogeneo della riga di risonanza.
Conclusioni
Lo scopo di questo lavoro di tesi è quello di verificare le previsioni dei recenti modelli di
superconduttività nonadiabatica [13, 24, 14, 7], i quali indicano la presenza di effetti isotopici
anomali nelle proprietà elettroniche in fase normale di nuovi materiali superconduttori quali
le fulleriti. In particolare essi prevedono un effetto isotopico sulla suscettibilità di spin [8, 7],
la quale, a causa dei nuovi canali di interazione nonadiabatici presenti, assumerebbe una
dipendenza dalla massa isotopica, dipendenza totalmente assente nel contesto adiabatico
convenzionale.
Il lavoro sperimentale riguarda la fullerite K3 C60 considerata rappresentativa del comportamento dei superconduttori fullerenici. Al fine di verificare, in questo composto, la presenza
di effetti isotopici sulla suscettibilità di Pauli, sono state impiegate due tecniche sperimentali quali la magnetometria SQUID e la risonanza magnetica nucleare NMR. In primo luogo
sono state effettuate misure SQUID, sia su campioni costituiti da una abbondanza naturale
di
13 C
(1.07%), sia su campioni arricchiti all’85%. I campioni arricchiti mostrano valori di
suscettibilità sistematicamente minori di quelli ottenuti dai campioni normali, diversamente
da quanto previsto dai modelli teorici che indicano un aumento della suscettibilità di Pauli
all’aumentare della massa isotopica.
I risultati delle misure SQUID sono stati confermati anche da successive misure di risonanza magnetica nucleare, attraverso la misura del Knight shift che origina dall’interazione
fra elettroni di conduzione e spin nucleari. Una prima valutazione della parte isotropa di questa interazione, nei campioni con differente abbondanza isotopica, mostra che nei campioni
arricchiti il Knight shift è minore che nei campioni costituiti da un’abbondanza naturale di
13 C.
È stato messo a punto l’apparato simulativo necessario ad estendere una simile verifica a
tutta l’interazione tensoriale fra elettroni e nucleo, che può essere dedotta solo da un’analisi
della forma di riga misurata in condizioni statiche. Le fulleriti sono cristalli plastici e quindi
le molecole di C60 sono soggette a moti di rotazione che mediano a zero l’anisotropia dell’interazione, che quindi, per essere ricavata, necessita di misure di risonanza magnetica nucleare a
bassa temperatura, dove i moti rotazionali dei fullereni sono congelati. Tali misure sono state
effettuate ad una temperatura superiore alla temperatura critica del K3 C60 , (Tc =19.2 K), in
81
82
4. Simulazioni della forma di riga NMR
modo da non innescare la transizione allo stato superconduttivo che svuota di elettroni la
banda di conduzione modificando cosı̀ radicalmente le proprietà magnetiche del sistema.
È stato effettuato, infine, un confronto fra le misure a 30 K sui campioni arricchiti, e una
preliminare simulazione della forma di riga basata sui parametri che definiscono i tensori di
Knight shift nel K3 C60 costituito da un’abbondanza naturale di 13 C. Sebbene da tale confronto emerga una chiara similitudine nella forma di riga, è comunque osservabile una differente
asimmetria che origina da una diversa interazione tensoriale di Knight shift. Opportune simulazioni potranno portare alla precisa determinazione delle interazioni tensoriali nei due
casi.
I risultati ottenuti sulla suscettibilità di spin confermano dunque la presenza di un effetto isotopico, anche se i modelli nonadiabatici citati non sono in grado di predire in modo
corretto la fenomenologia riscontrata. Una possibile spiegazione della riduzione riscontrata
nella suscettibilità di spin può derivare da una trattazione che tenga conto in modo adeguato
del disordine isotopico presente nei campioni arricchiti, a causa della rimanente percentuale
di
12 C
in essi presente (15%). A questo proposito una riduzione consistente della suscetti-
bilità di Pauli è stata prevista da pubblicazioni teoriche [28, 9] relative all’effetto che può
avere, in superconduttori nonadiabatici, la presenza di disordine determinato da impurezze
non magnetiche. Tali modelli rappresentano essenzialmente una trattazione degli effetti di
scattering fra elettroni e impurezze in presenza di un’interazione elettrone−fonone di tipo
nonadiabatico.
Una estensione di queste teorie al caso di disordine isotopico intramolecolare è tuttora in
fase di elaborazione.
Bibliografia
[1] Abragam, A. The Principles of Nuclear Magnetism. No. 32 in The International Series of
Monographs on Physics. Clarendon Press, Oxford, 1983.
[2] Alexandrov, A. S., and Kabanov, V. V. Theory of superconducting Tc of doped fullerenes.
Physical Review B 54, 5 (August 1966), 3655–3661.
[3] Alloul, H., Holczer, K., Yoshinari, Y., and Klein, O. 39 K NMR Study of Phase
transitions and Electronic Properties in K3 C60 . Physica C 235-240 (1994), 2509–2510.
[4] Ashcroft, N. M., and Mermin, N. D. Solid State Physics. HRW International Editions,
Philadelphia, 1976.
[5] Baskaran, G., and Tosatti, E. A theory of the normal and superconducting states of doped
solid C60 . Current Science 61, 1 (1991), 33–39.
[6] Caldirola, P., Cirelli, R., and Prosperi, G. M. Introduzione alla Fisica Teorica, 2nd ed.
Utet, Torino, 1996.
[7] Cappelluti, E., Grimaldi, C., L.Pietronero, and Strässler, S. Nonadiabatic channels
in fullerene compounds. In Electronic Properties of Molecular Nanostructures (New York, 2001),
H. Kuzmany, J. Fink, M. Mehring, and S. Roth, Eds., vol. 591 of AIP Conf. Proceedings, American
Institute of Physics, pp. 92–96.
[8] Cappelluti, E., Grimaldi, C., and Pietronero, L. Nonadiabatic Pauli susceptibility in
fullerene compounds. Physical Review B 64 (September 2001), 125104.
[9] Cappelluti, E., Grimaldi, C., and Pietronero, L. Spin susceptibility in small Fermi
energy systems: effects of nonmagnetic impurities. European Physical Journal B 30 (December
2002), 511–517.
[10] Cappelluti, E., Grimaldi, C., Pietronero, L., Strässler, S., and Ummarino, G. A.
Superconductivity in Rb3 C60 : breakdown of the Migdal-Eliashberg theory. European Physical
Journal 21 (March 2001), 383–391.
[11] Chakravarty, S., Kivelson, S., Salkola, I., and Tewari, S.
superconducting fullerenes. Science 256 (1992), 1306–1308.
Isotope effect in
[12] Grimaldi, C., and Pietronero, L. Pauli susceptibility of nonadiabatic Fermi liquids.
Europhysics Letters 47, 6 (September 1999), 681–687.
[13] Grimaldi, C., Pietronero, L., and Strässler, S. Nonadiabatic Superconductivity:
Electron-Phonon Interaction Beyond Migdal’s Theorem. Physical Review Letters 75, 6 (August
1995), 1158–1161.
[14] Grimaldi, C., Pietronero, L., and Strässler, S. Nonadiabatic Superconductivity II:
Generalized Eliashberg equations beyond Migdal’s theorem. Physical Review B 52, 14 (October
1995), 10530–10546.
[15] Grimaldi, G., Pietronero, L., and Scattoni, M. The physical origin of the electron-phonon
vertex correction. European Physical Journal B 10 (January 1999), 247–255.
83
84
Bibliografia
[16] Gunnarsson, O. Superconductivity in fullerides. Reviews of Modern Physics 69, 2 (April 1997),
575–606.
[17] Haddon, R. C. et al. Experimental and theoretical determination of the magnetic susceptibility
of C60 and C70 . Nature 350 (March 1991), 46–47.
[18] Hodgkinson, P., and Emsley, L. Computer simulation of solid-state NMR experiments.
Progress in Nuclear Magnetic Resonance Spectroscopy 36 (August 1999), 201–239.
[19] Landau, L. D., Lifs̆its, E. M., and Pitaevskij, L. P. Fisica statistica, 2nd ed. No. 5 in
Fisica teorica. Editori Riuniti, Edizioni Mir, Roma, 1986.
[20] Mazin, I. I., Dolgov, O. V., Golubov, A., and Shulga, S. V. Strong-coupling effects in
alkali-metal-doped C60 . Physical Review Letters 47, 1 (January 1993), 538–541.
[21] Mehring, M. Principles of High Resolurion NMR in Solids, 2nd ed. Springer Verlag, Berlin,
1983.
[22] Pennington, C. H., and Stenger, V. A. Nuclear magnetic resonance of C60 and fulleride
superconductors. Reviews of modern Physics 68, 3 (July 1996), 855–910.
[23] Pennington, C. H., Stenger, V. A., Recchia, C. H., Hahm, C., Gorny, K., Nandor,
V., Buffinger, D. R., Lee, S. M., and Ziebarth, R. P. 13 C NMR hyperfine couplings, T1
anisotropy, and Korringa relations in Rb2 CsC60 : Search for effects of strong correlation. Physical
Review B 53, 6 (February 1996), R2967.
[24] Pietronero, L., Strässler, S., and Grimaldi, C. Nonadiabatic superconductivity I: Vertex
corrections for the electron-fonon interactions. Physical Review B 52, 14 (October 1995), 10516–
10529.
[25] Riccò, M., Shiroka, T., Sartori, A., Bolzoni, F., and Tomaselli, M. Electronic
properties of (NH3 )x NaK2 C60 . Europhysics Letters 53, 6 (March 2001), 762–768.
[26] Sakurai, J. J. Meccanica Quantistica Moderna, 2nd ed. Zanichelli, Bologna, 1996.
[27] Sato, N., Tou, H., Maniwa, Y., Kikuchi, K., Suzuki, S., Achiba, Y., Kosaka, M.,
and Tanigaki, K. Analysis of 13 C-NMR spectra in C60 superconductors: Hyperfine coupling
constants, electronic correlation effect, and magnetic penetration depth. Physical Review B 58,
18 (November 1998), 12433–12440.
[28] Scattoni, M., Grimaldi, C., and Pietronero, L. Anomalous impurity effects in
nonadiabatic superconductors. Europhysics Letters 47, 5 (September 1999), 588–594.
[29] Schluter, M., Lannoo, M., Needels, M., Baraff, G. A., and Tománek, D. ElectronPhonon Coupling and Superconductivity in Alkali-Intercalated C60 Solid. Physical Review Letters
68, 4 (January 1992), 526–529.
[30] Schuh, S., and Martı́nez, G. Nonadiabatic superconductivity in K3 C60 and Rb3 C60 . Physica
B 320 (2002), 326–329.
[31] Slichter, C. P. Principles of Magnetic Resonance, 3rd ed. No. 1 in Springer series in solid-state
sciences. Springer Verlag, Berlin, 1990.
[32] Smith, S. A., Levante, T. O., Meier, B. H., and Ernst, R. R. Computer Simulations
in Magnetics Resonance. An Object-Oriented Programming Approach. Journal of Magnetic
Resonance 106 (August 1994), 75–105.
[33] White, S. R., Chakravarty, S., Gelfand, M. P., and Kivelson, S. A. Pair binding in
small Hubbard-model molecules. Physical Review B 45, 9 (March 1992), 5062–5065.
[34] Yoshinari, Y., Alloul, H., Brouet, V., Kriza, G., Holczer, K., and Forro, L. Molecular motion and phase transition in K3 C60 and Rb3 C60 by nuclear magnetic resonance. Physical
Review B 54, 9 (September 1996), 6155–6166.
Bibliografia
85
[35] Yoshinari, Y., Alloul, H., Kriza, G. G., and Holczer, K. Molecular motion and phase
transition in K3 C60 : A 13 C NMR Study. Physical Review Letters 71, 15 (October 1993), 2413–
2416.