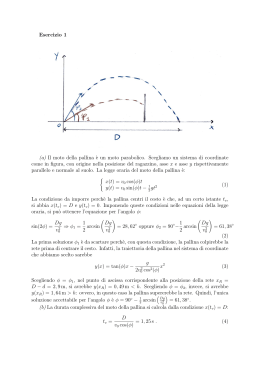
Soluzione dell'equazione differenziale del moto armonico
Il moto armonico è quello di un punto materiale la cui accelerazione a obbedisce alla
legge a = !" 2 x dove ω è una costante. Questa condizione da luogo all'equazione
differenziale
d2x
= !" 2 x
(1)
2
dt
la quale ammette la soluzione
x(t) = Asin(! t + " )
(2)
dove A e ϕ sono due costanti determinate dalle condizioni iniziali. La (2) si può
calcolare in maniera empirica o mediante integrazione diretta.
Soluzione empirica
La (1) è un'equazione differenziale lineare del 2˚ ordine a coefficienti costanti. Per
questo tipo di equazioni vale un teorema che dice che date due funzioni f1 (t) e
f2 (t) che siano due soluzioni indipendenti, tali cioe' che f1 (t) f2 (t) ! costante , allora
la soluzione generale della (1) si scrive:
x(t) = S f1 (t) + C f2 (t)
(3)
dove S e C sono due costanti. Verifichiamo che la funzione f1 (t) = sin ! t è una
soluzione della (1). Infatti abbiamo:
d
(sin ! t ) = ! cos ! t
dt
(4)
d2
d
d
(sin ! t ) = (! cos ! t ) = ! (! cos ! t ) = "! 2 sin ! t
2
dt
dt
dt
(5)
e quindi effettivamente la (1) risulta soddisfatta. Allo stesso modo si verifica che
anche la funzione f2 (t) = cos ! t è soluzione della (1). Queste due soluzioni sono
indipendenti perche evidentemente risulta sin ! t cos ! t = tan ! t " costante . Quindi la
soluzione generale della (1) è:
x(t) = S sin ! t + C cos ! t
(6)
Verifichiamo adesso che la soluzione generale (6) si puo scrivere come
S sin ! t + C cos ! t = Asin(! t + " )
-1-
(7)
A questo scopo determiniamo quali debbano essere i valori di A e ϕ affichè valga la
(7). Applicando le formule trigonometriche di addizione al membro di destra si
ottiene
S sin ! t + C cos ! t = A ( sin ! t cos " + cos ! t sin(" )
= A cos " sin ! t + Asin " cos ! t
(8)
I due membri a destra e sinistra devono essere uguali per ogni valore di t. Questo può
avvenire solo se
S = A cos !
C = Asin !
(9)
Sommando queste due equazioni dopo averle elevate al quadrato si trova:
S 2 + C 2 = A 2 cos 2 ! + A 2 sin 2 !
(
= A 2 cos 2 ! + sin 2 !
)
(10)
= A2
dato che il termine in parentesi vale 1. Si trova quindi:
A = S2 + C 2
(11)
Invece dividendo la seconda delle (9) per la prima:
C Asin !
=
= tan !
S A cos !
(12)
" C%
! = arctan $ '
# S&
(13)
per cui:
con !90˚" # " 90˚ . Queste relazioni esprimono il legame fra le costanti S e C della
(7) e le costanti A e ϕ della (6). Quindi la posizione, la velocità e l'accelerazione nel
moto armonico si scrivono:
x ( t ) = Asin (! t + " )
d
# Asin (! t + " ) %& = ! A cos (! t + " )
dt $
d
a ( t ) = #$! A cos (! t + " ) %& = '! 2 Asin (! t + " )
dt
v (t ) =
(14)
La soluzione (7) si puo scrivere anche utilizzando la funzione coseno. Infatti ponendo
! = " 2 + ! # si ottiene:
-2-
$(
%
x ( t ) = Asin (! t + " ) = Asin ' ! t + " # + * = A cos (! t + " # )
&
2)
(15)
Si noti comunque che le espressioni (6), (7) e (15) sono solo tre modi diversi di
scrivere la stessa funzione. Le costanti A e ϕ sono determinate dalle condizioni
iniziali. Infatti dette x0 e v0 i valori iniziali della posizione della velocità abbiamo:
x0 = x ( 0 ) = Asin !
(16)
v0 = v ( 0 ) = " A cos !
da cui si ottiene:
v02
x + 2 = A 2 sin 2 " + A 2 cos 2 " = A 2 sin 2 " + cos 2 " = A 2
!
(17)
v02
A= x + 2
!
(18)
! x0 Asin "
=
= tan "
v0
A cos "
(19)
(
2
0
)
e quindi
2
0
Inoltre:
L'equazione
tan ! =
" x0
v0
(20)
ammette le due soluzioni
# "x &
!1 = arctan % 0 (
$ v0 '
) 90˚* ! * 90˚
# "x &
! 2 = arctan % 0 ( + 180˚
$ v '
(21)
90˚* ! * 270˚
0
per le quali va accertata l'accettabilita' verificando i valori di x0 e v0 dalle (16).
Significato delle costanti A e ϕ
Dato che risulta –1 ≤ sin(ωt+ϕ) ≤ 1, la costante A rappresenta l’ampiezza massima
delle oscillazioni rispetto alla posizione centrale x=0. La costante ϕ è determinata,
(come A) dai valori iniziali x0 e v0, cioè dai valori di x e v per t=0. Ad esempio, se a
t=0 l’oscillazione parte dal centro del moto, allora x0=0 e si ha A=v0/ω e ϕ =0. In
questo caso la soluzione (39) diventa
x = Asin ! t
-3-
(22)
Se invece a t=0 l’oscillazione parte da un punto corrispondente all’estremità positiva
della massima oscillazione, laddove la velocità inverte il segno, allora v0=0 e quindi
A=x0 e ϕ=π/2. In questo caso abbiamo:
"&
#
x = Asin % ! t + ( = A cos ! t
$
2'
(23)
Soluzione diretta (facoltativa)
La soluzione della (1) si può anche ricavare direttamente. A questo scopo nella (1)
scriviamo d2x/dt2 = dv/dt. Inoltre moltiplichiamo per v entrambi i membri, avendo
l’avvertenza di scrivere v come dx/dt nel membro di destra. Si trova:
dv
dx
v = !" 2 x
dt
dt
(24)
Semplificando la quantità dt si ricava un’equazione a variabili separate:
vdv = !" 2 xdx
(25)
Per risolverla integriamo ambo i membri scegliendo estremi di integrazione
corrispondenti: mentre la velocità passa dal valore iniziale v0 ad un generico valore v,
la posizione passa dal valore iniziale x0 al generico valore x
v
"
$ v! dv!
$
$
#
x
= %&
"
2$
$
$
#
v0
x ! dx !
(26)
x0
Risolvendo gli integrali si trova
1 2 1 2
1 &
#1
v ! v0 = !" 2 % x 2 ! x02 (
$2
2
2
2 '
(27)
che si può scrivere
(
v = v02 ! " 2 x 2 ! x02
)
(28)
Questa relazione rappresenta la velocità nel moto armonico in funzione della
posizione x. Per ricavare la legge oraria integriamo ulteriormente. Riscriviamo la (28)
come
(
dx
= v02 ! " 2 x 2 ! x02
dt
Separando le variabili si trova:
-4-
)
(29)
dx
(
v02 ! " 2 x 2 ! x02
= dt
)
(30)
Raccogliendo ω nel denominatore e portandolo al secondo membro otteniamo:
dx
v02
+ x02 " x 2
!2
= ! dt
(31)
Integriamo ambo i membri scegliendo per semplicità t0 = 0:
x
$
&
&
&
&
%
x0
t
dx !
2
0
2
v
+ x02 # x ! 2
"
=
$
" && dt !
&
%
(32)
0
Nelle tavole degli integrali si trova:
"
$
$
#
% x(
= arcsin ' *
& a)
a !x
dx
2
2
(33)
e quindi, identificando nella (32) la quantità v02 ! 2 + x02 con la costante a2 abbiamo
#
%
%
%
%
$
&
)
(
+
dx
x
+
= arcsin (
( v02
v02
2
2
2 +
+ x0 " x
+ x0 +
('
*
!2
!2
(34)
e quindi, risolvendo gli integrali nella (32)
#
&
%
(
x!
%
(
arcsin
% v02
(
+ x02 (
%$
2
'
"
x
= "t
x0
#
&
#
&
%
(
%
(
x
x0
( ) arcsin %
( = "t
arcsin %
2
% v02
(
%
(
v
0
+ x02 (
+ x02 (
%$
%
2
2
'
$ "
'
"
Adesso osservo che il secondo termine e' una costante. Allora posto
-5-
(35)
#
&
%
(
x0
(
! = arcsin %
% v02
(
+ x02 (
%$
2
'
"
(36)
"
%
$
'
x
' = !t + (
arcsin $
$ v02
2 '
+ x0 '
$#
&
!2
(37)
troviamo
da cui, posto anche
A=
v02
+ x02
2
!
(38)
si trova alla fine:
x = Asin (! t + " )
(39)
che coincide con la soluzione gia trovata in maniera empirica. Si osservi inoltre che,
dato che risulta sempre –1 ≤ sin(ωt+ϕ) ≤ 1, dalla (39) risulta x2≤A2
e quindi
v02
2
x ! 2 + x02
(40)
"
il che assicura che la radice quadrata nella (28) e seguenti è sempre un numero reale.
-6-