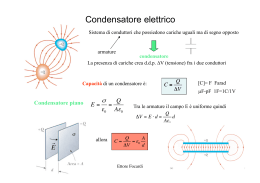
Dielettrici (Isolanti)
N.B. nelle operazioni che svolgeremo avremo a che fare con condensatori
carichi. Si può operare in due diverse condizioni:
1) a carica costante: condensatore caricato e poi scollegato dal generatore
2) a potenziale costante: condensatore sempre collegato al generatore
Dielettrici
1
Carica costante
Inseriamo una lastra metallica tra le armature di un condensatore carico
lastra metallica
V
V0
Q costante , V < V0, C = Q/V aumenta
Equivale ad un condensatore di separazione tra le due armature d = h-s
Dielettrici
2
Inseriamo una lastra di dielettrico (isolante):
(
)
prima, lastra di spessore < separazione fra le armature : V’ < V0 (a)
poi in modo da riempire tutto lo spazio fra le armature Vk < V’ < V0 (b)
Definiamo costante dielettrica (relativa) del dielettrico, k ,il rapporto
Dielettrici
3
Allora:
con ε = k ε0 ( costante dielettrica assoluta/ permettività
p
del dielettrico))
e σp = σ0 /k
Calcoliamo l’extra-campo elettrico prodotto dal dielettrico, Ei
Ei =
La χ (chi) si definisce “ suscettività dielettrica”
Dielettrici
4
All’i t
All’interno
d l dielettrico
del
di l tt i sii forma
f
un campo elettrico
l tt i (di polarizzazione)
l i
i )
(Ei ) di segno opposto a quello tra le armature del condensatore (E0) , per
cui il campo totale (Ek) decresce. Ek = Eo - Ei
Sulle facce del dielettrico compare una densità di carica, σp, di segno
opposto a quella sulle armature di fronte , ma di valore minore
+
Dielettrici
E0
+ $+
Ei
+
+
5
N B Le cariche sulle armature e quelle sul dielettrico non possono combinarsi,
N.B.
combinarsi
perché quelle sul dielettrico non sono cariche mobili e quelle sulle armature non
possono entrare
t
nell dielettrico
di l tt i che
h è isolante.
i l t
Se moltiplichiamo le σ per l’area delle armature ,Σ, otteniamo le cariche
totali. Quindi da
si ottiene
Dielettrici
6
La capacità di un condensatore pieno di dielettrico diventa
In particolare per il condensatore f.p.p. si ha
ε = kε0 si chiama costante dielettrica assoluta del dielettrico
Tutte le formule viste in precedenza per il condensatore vuoto, valgono anche
per quello
ll pieno
i
di dielettrico,
di l tt i se sii sostituisce
tit i
ε0 con ε.
Dielettrici
7
Si definisce Rigidità
g
dielettrica il ppiù elevato valore del campo
p elettrico nel qquale
può trovarsi il dielettrico prima che al suo interno comincino a scorrere delle cariche
(il dielettrico “si buca”)
Dielettrici
8
Esempio
Condensatore parzialmente riempito di dielettrico di cost. diel. k
Quanto valgono V’k e Ceq ?
Fuori dal dielettrico campo elettrico è
come nel cond. vuoto E = σ0/ε0 .
Nel dielettrico Ek = σ0/kε0
N.B. E non dipende
dalla pposizione del
p
dielettrico e V’k dipende solo dallo spessore
Dielettrici
9
V’k
Ceq
Come si vede il sistema equivale a due condensatori in serie, uno vuoto, di
separazione (h-s), e l’altro pieno di dielettrico di spessore s e costante k
Dielettrici
10
Potenziale costante
Il condensatore è sempre collegato a un generatore che mantiene costante
la d.d.p. ai suoi capi, V0 , facendo variare, se necessario la carica sulle
armature.
Cond. vuoto:
Dielettrici
11
Con dielettrico C = k C0 , quindi:
Il generatore deve fornire una l’extra-carica qp , producendo un lavoro
W = qp V0
Dielettrici
12
Forza di risucchio su una lastra di dielettrico
In un condensatore a f.p.p.,
p p di lato l e separazione
p
h, collegato
g
a un
generatore, è inserita una lastra di dielettrico per una lunghezza x.
N.B. Il campo elettrico non è (mai) uniforme in prossimità dei bordi!
Cosa succede?
Dielettrici
13
Il campo del condensatore interagisce con le cariche indotte sul dielettrico
(anche fuori dalle armature).
Consideriamo il sistema come due
cond (uno pieno e uno vuoto) in
cond.
- -- --+ ++ +++
parallelo
se x aumenta
u e
di
d dx,, (la
( lastra
s eentra ddi ppiù
ù tra lee armature)
u e) C ccresce
esce di
d dC
C
con spostamento della carica dq = VdC da una faccia all’altra ad opera del
generatore
Dielettrici
14
Il generatore compie un lavoro
l’energia elettrostatica aumenta di
L’altra metà del lavoro del generatore viene fatto tramite la forza di risucchio
N.B. il segno di F
Dielettrici
15
Polarizzazione dei dielettrici
Di che
h natura
t
è la
l carica
i che
h appare sulle
ll facce
f
del
d l dielettrico?
di l tt i ?
Un dielettrico sottoposto a un campo elettrico si dice polarizzato
Struttura dei dielettrici:
Elementi (atomi o molecole) senza (1) o con (2) momento di dipolo spontaneo.
1) Senza m.d.d.
Es.atomo
Effetto del campo elettrico esterno: Spostamento dei
“baricentri” delle cariche + e -, con formazione di un
m.d.d. indotto: p = Zex
Dielettrici
16
2) Molecole con m.d.d. spontaneo p0 (es. H2O)
Effetto del campo esterno: orientazione media dei dipoli.
dipoli
E’ come
se all’interno del dielettrico si
formassero delle catene di dipoli (efficaci)
da una faccia all’altra.
Dielettrici
14
Supponiamo di individuare un volumetto cubico τ all’interno del
dielettrico polarizzato, che contenga N atomi o molecole, ognuno con
m.d.d. medio <p>
Il m.d.d. totale è p = N <p> .
Definiamo Momento di dipolo per unità di volume
n = densità di atomi o molecole (m-3),
Il vettore P (sempre // a E) si definisce anche Polarizzazione (del dielettrico)
U ità di misura:
Unità
i
<p>:
< > C m; P : C m / m3 = C //m2 = densità
d ità superficiale
fi i l di
carica.
Dielettrici
18
Prendiamo un volumetto, dτ, all’interno del dielettrico polarizzato di area dΣ0
e spessore dh, nella direzione di P e E, il suo m.d.d. è: dp = P dτ
Possiamo sostituirlo con un altro sistema che non alteri il m.d.d.
m d d totale ?
Sostituiamolo con due lamine metalliche di area dΣ0 e separate di dh.
Che carica dq dobbiamo mettere sulle armature pe avare lo stesso m.d.d.?
P dτ = dq dh = σp dΣ 0 dh = σ dτ
quindi σp = P e dq = P dΣ0
Dielettrici
19
Se ora consideriamo due cubetti adiacenti, le cariche –dq e +dq sulle due
facce in contatto si annullano e restano solo le cariche –dq e +dq sulle
facce estreme, ad una distanza 2dh.
Continuando ad aggiungere cubetti si arriva alle due superfici
Quindi sulle facce di una lastra di dielettrico polarizzato è presente una carica
di polarizzazione di densità σp = |P|
Dielettrici
20
Se il dielettrico non ha forma regolare, dato un prismetto di superficie,
sulla faccia interna –dq = σ’p dΣ0 = P dΣ0 mentre sulla faccia esterna
dq = σp dΣ , quindi
Se 0 < θ < π/2
σp > 0, se π/2 < θ < π
σp < 0
Per una lastra θ = 0 e θ = π
Dielettrici
21
In generale (cristalli cubici. amorfi,…) P ∝ E:
P = ε0 χ E = ε0 (κ-1) E
quindi χ è uno scalare.
Ma per i cristalli χ può essere un tensore! Pi = ε0 Σj χij Ej
D
Dato
che
h le
l cariche
i h di polarizzazione
l i
i
qp sono
cariche “vere”, possiamo inserirle nella Legge di
Gauss applicata alla scatola cilindrica in figura,
con la base (di area Σ ) parallela alle armature.
Dielettrici
22
Calcoliamo il flusso di P attraverso la stessa superficie chiusa Σ
Considerando che P è nulla all’interno
all interno delle armature si ha
= σpΣ = qp
per cui
(cariche libere)
Dielettrici
23
Definiamo D il vettore Induzione Dielettrica.
Quindi le Legge di Gauss in presenza di dielettrici, si può scrivere
(=D
Σ …)
Il modulo di D coincide con la densità di cariche libere σ
Come si vede P e D e σ hanno le stesse dimensioni quindi le stesse unità di
misura: C / m2
Dielettrici
24
In un dielettrico in un C.F.P.P.
La forma locale della Legge di Gauss in presenza di un dielettrico diventa:
Dielettrici
25