Università degli studi di Torino
Facoltà di Scienze M.F.N.
Corso di Studi in Fisica
Accoppiamento dell’indice di
rifrazione in fluidi stratificati
Esame di alcuni aspetti
sperimentali
Candidato
Ilaria Tabone
Relatore
Prof. C. Cassardo
Co-Relatore
Dott. M. Manfrin
1
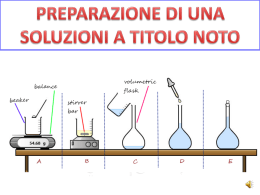
Tecnica della Particle
Image Velocimetry (PIV)
•
Utilizzata per studi di fluidodinamica
•
Indaga comportamento e proprietà dei fluidi tramite il moto di particelle
traccianti nel fluido in esame, illuminate da una luce laser e riprese da
una videocamera
•
Un’analisi al computer ricostruisce il campo delle velocità delle
microparticelle e quindi il moto del fluido
2
Tecnica della Particle
Image Velocimetry (PIV)
•
utilizzata nel laboratorio di
Geofluidodinamica
•
può essere impiegata in
fluidi omogenei o in fluidi
stratificati
3
Stratificazione
STABILE
INSTABILE
• fluido più denso sottostante
• fluido più denso sovrastante
quello meno denso
quello meno denso
• configurazione più semplice
• moti convettivi
da gestire
configurazione
caotica/complessa
EQUILIBRIO
ho utilizzato fluidi stratificati stabili
4
Fluidi stratificati
Diverse densità e quindi diversi indici di rifrazione
c
n=
v
n assoluto
n relativo
n1,2 =
n
n
2
1
fluido omogeneo
=
senϑ 1
senϑ 2
fluido stratificato
La luce viene rifratta
diversamente
a seconda del fluido
che attraversa
Immagini sfocate
Particelle non visibili
5
Matching
Si cerca di rendere il più possibile uguali gli indici di rifrazione dei fluidi in
esame, variando la concentrazione dei diversi soluti nelle soluzioni,
mantenendo la stratificazione
Importante nell’interfaccia tra i due mezzi
dove c’è MISCELAMENTO
Potrei aspettarmi in prima approssimazione che, unendo le due
soluzioni con lo stesso indice di rifrazione, ottenga una nuova soluzione
miscelata con lo stesso indice di rifrazione di partenza
6
Mc Dougall* (1978)
Ho trovato in letteratura un’equazione che esprime la variazione di n in funzione
1) delle concentrazioni dei soluti nella miscela
- Epsom salt (solfati di magnesio)
- Zucchero
2) delle loro proporzioni
Peso della soluzione di zucchero
m = Peso della soluzione totale
RAPPORTO DI
MESCOLANZA
* Mc Dougall, On the elimination of refractive-index variations in turbolent density-stratified liquid flows
7
Mc Dougall
Quando due soluzioni con lo stesso n vengono miscelate, l’indice di rifrazione della soluzione
finale può variare a seconda delle proporzioni con cui ho miscelato le soluzioni iniziali e delle
concentrazioni iniziali dei soluti
n(CA1,CB2,m) = 1.3330 + 0.20286 (1-m) CA1 - 0.0061 (1-m)2 C2A1
+ 0.14445 m CB2 + 0.043 m2 C2B2 + 0.158 m (1-m) CA1CB2
CA1 = concentrazione di sale Epsom
CB2 = concentrazione di zucchero
nella soluzione 1
nella soluzione 2
Variazione dell’indice di rifrazione in funzione del rapporto di mescolanza
x 10-4
10
∆n
T = 20°C
5
0
0.4
0.2
0.6
Peso della soluzione di zucchero
m=
Peso della soluzione totale
0.8
1.0
8
In vasca si utilizzano soluti
diversi
SALE (NaCl)
varia meno n rispetto a ρ
al variare delle concentrazioni
di sale nella soluzione
GLICERINA
varia più n rispetto a ρ
al variare delle concentrazioni
di glicerina nella soluzione
Combinando insieme queste due proprietà possiamo creare soluzioni
con concentrazioni diverse tra loro, indice di rifrazione simile, pur
mantenendo differenze di densità notevoli
9
Scopo iniziale del mio
lavoro
Verificare che i soluti utilizzati in vasca
(sale e glicerina) abbiano un
comportamento simile a quello descritto da
Mc Dougall e cercare di determinarlo
quantitativamente
10
Verifica della variazione di n in
tre soluzioni diverse, in funzione
del rapporto di mescolanza
Ho preparato
3 soluzioni di H2O e sale
3 soluzioni di H2O e glicerina
S [%]
G [%]
4
6
ρ=1.028
1.028
g/cm3
ρ=1.013
1.013
g/cm3
11
16
ρ=1.077
1.077
g/cm3
ρ= 1.035
g/cm3
18
26
ρ= 1.131
g/cm3
ρ= 1.062
g/cm3
n
1.3400
1.3520
T=23.3 °C
miscelando le coppie di
soluzioni con lo stesso n
ho ottenuto 3 soluzioni
finali
1.3650
11
Rifrattometro
•
•
•
•
sensibilità
±1*10-4
errore
± 2*10-4
sensibilità termometro
± 0.1°C
errore sulle T
± 1°C
Densimetro
•
•
•
•
sensibilità
± 1*10-4 g/cm3
errore
± 1*10-3 g/cm3
sensibilità termometro
± 0.1°C
errore sulle T
± 0.2°C
12
...Come procedo nella misurazione?
•
miscelo le due soluzioni variando il rapporto di mescolanza
m=
•
Peso soluzione acqua e sale
Peso soluzione totale
misuro n e ρ al variare di m, a T = 23.3°C
(6 misure ripetute e medio i valori)
l’effetto è più
evidente al
crescere di n di
partenza
Per n bassi e quindi per
soluzioni poco concentrate,
la variazione dell’indice di
rifrazione è ridotta,
nell’ambito dell’errore del
rifrattometro
n-n0= scarto tra n
misurato e n iniziale
n3=1.3650
n2=1.3520
n1=1.3400
13
In vasca
•
•
è quindi conveniente lavorare con soluzioni con n basso
per eseguire il matching mi è utile essere in grado di valutare gli n delle soluzioni a
T precise (15°C<T<25°C)
cerco un’equazione che mi permetta di ottenere gli n per diverse T
MISCELA
• dipende da T, S e G (e loro proporzioni)
• dipende quadraticamente dalle concentrazioni
H2O e glicerina
H2O e sale
14
Acqua e glicerina
•
Non ho trovato in letteratura un’equazione che esprimesse l’andamento di n in funzione di
G, T e λ. Ho pensato di ricavarla sperimentalmente, misurando n a diverse G e T
(17°C<T<24°C)
•
Non posso lavorare sulla dipendenza di λ
la fisso a quella del rifrattometro, non nota
L’andamento dell’indice di rifrazione al
variare di T e G può essere espresso
dall’equazione da me ricavata:
n(T,G) = 1.335 – 6.542*10-5 T + 1.058*10-3 G - 1.108*10-6 T G + 1.388*10-5 G2 –
3.994*10-9 T G2 - 2.717*10-7 G3
15
Acqua e sale
Ho trovato in letteratura un’equazione che esprime n in funzione di T, S (%) e λ
X.Quan – E.Fry * (1995)
n(S,T,λ) = a0 + (a1 + a2T + a3T2)*S + a4T2 + (a5 + a6S + a7T)/λ + a8/λ2 + a9/λ3
• riferita all’acqua marina standard
• valida per salinità <4%
• 0°C <T<30°C
PROBLEMI
non conosco la λ di lavoro del rifrattometro
ma dovrebbe essere intorno al doppietto del sodio
potrebbe non descrivere completamente il
comportamento di acqua + NaCl
* X.Quan and E.Fry, Empirical equation for the index of refraction of seawater (1995)
16
Ricerca della λ di lavoro
del rifrattometro
ACQUA DISTILLATA
•
•
Misuro l’indice di rifrazione a diverse T e sostituisco i valori di T all’interno
dell’eq di Fry per acque non saline
Confrontando l’andamento di n di Fry (S=0%) con quello misurato,noto che per
nessuna λ i due andamenti si accoppiano perfettamente. Scelgo una λ che
meglio eguaglia i due andamenti
17
La lunghezza d’onda di
lavoro del rifrattometro
trovata è
λ = 580 nm
18
Provo ad applicare l’andamento di Fry ad
una soluzione di acqua + NaCl
•
•
Preparo una soluzione con salinità crescente da S=0.2% a S=4% e misuro n
•
Confronto l’andamento di n(S,T,λ) di Fry con n misurato sperimentalmente
Sostituisco nell’eq di Fry i valori di S, la λ trovata e la T alla quale sono state eseguite le
misure (costante) T = 20.6°C
pendenza
diversa
a S=0% vi è accordo...
evidentemente c’è un
effetto relativo
all’utilizzo del solo
NaCl nella soluzione!
Ricordo che l’equazione di Fry si
riferisce ad acque marine. La
discrepanza tra curva attesa e curva
sperimentale è molto probabilmente
dovuta a questa ipotesi
19
Questa discrepanza è probabilmente dovuta al fatto che
• la soluzione H2O e sale contiene solo NaCl
• l’acqua di mare contiene sali diversi e in diverse proporzioni
20
Verifico eventuali differenze nel
comportamento tra acque di mare (Menton Costa Azzurra) e soluzione di acqua + NaCl
•
•
Misuro n e ρ dell’acqua di mare a T costante = 22.8°C
Inserisco T e ρ nell’equazione di Millero & Poisson* (1980) e ricavo S per via numerica
ρ= ρ0+A(T)*S + B(T)*S3/2 + C*S2
ρ0= 999.842594 + 6.793952e-2*T - 9.095290e-3*T2 +
1.001685e-4*T3 - 1.120083e-6*T4 + 6.536336e-9*T5
valida per acque marine standard
S = 35.4 ‰
•
Riproduco una soluzione in laboratorio con la stessa salinità. Misuro n e ρ
DISCREPANZA TRA
I VALORI MISURATI
δn = 4*10-4
δρ = 1.5*10-3 g/cm3
* F.Millero and A.Poisson, International one-atmosphere equation of state of seawater (1980)
21
Ogni tipo di sale presenta, alla medesima concentrazione, un n diverso.
Potassium Chloride
Magnesium Chloride
Concentration vs. refractive index (20°C)
Concentration vs. refractive index (20°C)
Calcium Chloride
*
Concentration vs. refractive index (20°C)
% by wt.
nD
A % by wt.
nD
% by wt.
nD
0,50
1,3337
0,50
1,3343
0,00
1,3330
1,00
1,3343
1,00
1,3356
0,50
1,3342
1,50
1,3350
2,00
1,3381
1,00
1,3354
2,00
1,3357
3,00
1,3406
1,50
1,3366
2,50
1,3364
4,00
1,3432
2,00
1,3378
3,00
1,3371
5,00
1,3457
2,50
1,3390
3,50
1,3377
6,00
1,3483
3,00
1,3402
4,00
1,3384
7,00
1,3508
3,50
1,3414
4,50
1,3391
8,00
1,3534
4,00
1,3426
5,00
1,3398
9,00
1,3560
4,50
1,3438
5,50
1,3404
10,00
1,3587
5,00
1,3451
6,00
1,3411
12,00
1,3641
5,50
1,3463
6,50
1,3418
14,00
1,3695
6,00
1,3475
La somma dei diversi contributi di sali disciolti nell’acqua di mare fa sì che l’indice di
rifrazione totale sia diverso da quello misurato per la soluzione di acqua e NaCl
L’eq di Fry non descrive completamente l’andamento di n per
una soluzione di acqua e NaCl
* Mettler Toledo, Tabelle Indice di Rifrazione – Concentrazione (T=20°C)
22
Eq. di Fry corretta per soluzioni
di acqua e NaCl
T = 20.6°C
• Ho calcolato gli scarti tra la curva di n
misurato e quella di Fry
• Ho ricavato l’eq. che meglio
esprime
l’andamento degli scarti
n(S) = 1.9041*10-4 S – 6.3088*10-5
L’equazione di Fry corretta è
n(S,T,λ) = a0 + (a1 + a2T + a3T2)*S + a4T2 + (a5 + a6S + a7T)/λ
+ a8/λ2 + a9/λ3 – 1.9041*10-4*S + 6.3088*10-5
• T = 20.6 °C
• λ = 580 nm
• funzione unicamente di S
23
Considerazioni finali
Il comportamento del sale e della glicerina al variare della
concentrazione dei soluti nella miscela è simile a quello presentato da Mc
Dougall. Il problema del matching dell’indice di rifrazione viene risolto,
nell’ambito dell’errore del rifrattometro, se si utilizzano soluzioni con n
basso (poco concentrate)
Le equazioni ricavate per la soluzione di acqua e glicerina (nota T) e
per la soluzione di acqua e NaCl (a T=20.6°C e λ=580 nm) permettono
di determinare la quantità di glicerina o di sale che occorre per ottenere a
priori un particolare indice di rifrazione
PROPOSTE
La ricerca di un’equazione che esprima l’andamento di n anche in
funzione di T per soluzioni di NaCl e l’andamento di n(S,G,T) per la
miscela complessiva potrebbe essere oggetto di una tesi futura
24
25
Ringraziamenti
Ringrazio il Prof. Cassardo e il Dott. Manfrin per tutto il tempo che
pazientemente hanno dedicato a questa tesi e per avermi fatto
appassionare al mondo “della vasca”;
Ringrazio il Dott. Forza, che ha osato sfidare per me le mareggiate della Costa
Azzurra;
Ringrazio mamma, papà, amici fisici, non fisici e tutti voi che avete avuto la
pazienza di stare seduti fino alla fine!
...e come dimenticarvi??
Ringrazio (in ordine di altezza)
il Nonnerellorso, Rocco, Ari+ e ToniStar per avermi regalato tre anni davvero
INDIMENTICABILI!!
26
27
28
29
2
y
y
i
mis
Fry
y
2
zz
c = „ jj
k smedia {
~ 2
co =
errore
smedia = 8 * 10- 5
livello di significatività
del disaccordo
PIc ≥ co M < 1%
λ = 600nm
~ 2
co
~ 2
co
~ 2
co M~
0%
DF
λ = 580 nm
= 13.42
P Ic ≥
~2
DF=10
~ 2
λ = 589 nm
= 66.45
P Ic ≥
~2
~2
c2
~ 2
co M~
0%
~ 2
co
P Ic ≥
~2
= 0.36
~ 2
co M~
95 %
30
ij nmis - y yz2
c = „j
z
k smedia {
2
~2
DF
~ 2
smedia = 8 * 10- 5
errore
n(T) acqua e glicerina
co =
c2
PIc ≥ co M < 1%
livello di significatività
del disaccordo
Curve Mc Dougall
~ 2
~ 2
c o = 0.03
~ 2
co
P I c ≥ c o M ~ 100 %
~2
~ 2
P I c ≥ c o M ~ 100 %
~2
= 0.09
~ 2
n(T) ricerca lambda
c o = 0.2
n(S) acqua e sale
c o = 0.74
~ 2
~ 2
P I c ≥ c o M ~ 99 %
~2
~ 2
P I c ≥ c o M ~ 78 %
~2
~ 2
31
Coefficienti eq. di Millero & Poisson
• A(T) =
8.24493*10-1 – 4.0899*10-3T +
7.6438*10-5T2 – 8.2467*10-7T3 +
5.3875*10-9T4
• B(T) = -5.72466*10-3 + 1.0227*10-4T –
1.6546*10-6T2
• C = 4.8314*10-4
32
Coefficienti eq. Quan & Fry
a0 = 1.31405
a1 = 1.779*10-3
a2 = - 1.05*10-5
a3 = 1.6*10-7
a4 = - 2.02*10-6
a5 = 15.868
a6 = 0.1155
a7 = - 0.00423
a8 = - 4382
a9 = 1.1455*106
33
~G
~G^2
SSE=3.0951*10-6
SSE=6.7654*10-7
~G^3
SSE=2.0014*10-7
34
y=a+bx
A=
a
b
D=
N
Σ xi
Σ yi
Σ xi
Σ x i2
B=
Σ xi yi
A = D -1 B
Σ yi Σ xi
a=
det D Σ xi yi Σ xi2
1
b=
1
det D
N
Σ yi
Σ xi Σ xi yi
Σ x i2
σa2= σ2 det D
σb
2=
σ2
N
det D
35
y = a + b x + c x2
A=
Σ yi
Σ xi
Σ xi3
N
Σ yi
Σ xi Σ xi yi
Σ xi2 Σ xi 2yi
Σ xi2
Σ xi3
Σ xi4
N
Σ yi
1
c=
det D
Σ xi
B = Σ xi yi
σa2= σ2 ∑
∂a
∂yi
2
σb2= σ2 ∑
∂b
∂yi
2
σ2 ∑
∂c
∂yi
2
Σ xi4
Σ xi Σ xi 2 Σ xiyi
Σ xi2 Σ xi 3 Σ xi2yi
σc
2=
A = D-1 B
Σ xi 2 yi
Σ xi2
1
Σ xi yi Σ xi2
a=
det D Σ x 2y Σ x 3
i i
i
1
b=
det D
Σ yi
N
Σ xi Σ xi2
D = Σ xi Σ xi2 Σ xi3
Σ xi2 Σ xi3 Σ xi4
a
b
c
36