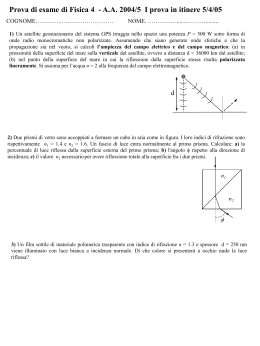
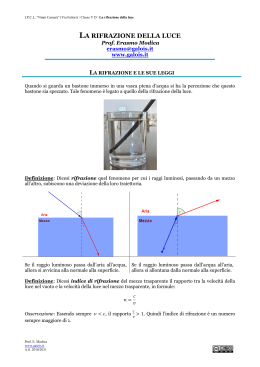
Prova di esame di Fisica 4 - A.A. 2009/10 I appello febbraio 8/2/15
COGNOME…………..………………………
NOME. ……………........……….........
1) Un prisma isoscele di vetro, con angoli alla base  = 30° e indice di rifrazione n1, è appoggiato sopra una lastra
di vetro con indice di rifrazione n2 a facce piane e parallele orizzontali. Un raggio di luce che si propaga in aria
orizzontalmente e con polarizzazione verticale è rifratto senza alcuna riflessione all’interno del prisma e quindi
subisce quindi una riflessione totale all’interfaccia con la lastra. Calcolare i valori di n1 e n2.
n1

n2
2) Una sfera di raggio R = 30 cm è fatta di un materiale trasparente. (a) Che valore deve avere l’indice di
rifrazione del materiale affinché i raggi del sole incidenti su una superficie siano focalizzati in un punto posto
sulla superficie diametralmente opposta? (b) assumendo l’irradiamento sulla superficie anteriore pari a I0 = 0.5
kW/m2 diaframmata da un’apertura di sezione A = 20 cm2, la distanza solare pari a 1.51011 m, il raggio solare
Rs = 0.5109 m, che valore avrà l’irradiamento nel fuoco?
A
C
3) Un oggetto è situato a una distanza di 5 cm da una lente sottile biconcava di vetro flint (con indice di
rifrazione n = 1.67) i cui raggi di curvatura delle superfici sono R1 = 7 cm e R2 = 12 cm. Calcolare posizione,
natura e ingrandimento dell’immagine e tracciare i raggi.
R1
R2
4) Un film sottile di materiale polimerico trasparente con indice di rifrazione n = 1.45 e spessore d = 200 nm
viene illuminato con luce bianca a incidenza normale. Di che colore si presenterà a occhio nudo la luce riflessa?
Corso di Fisica 4 – Soluzioni I appello di Febbraio 2011
1) Con riferimento alla figura:

r
i
γ
Per la condizione di Brewster deve essere:
n1
 tg  tg 60
na
 n1  1.732
Da Snell e Brewster ricaviamo:
sin 
n
sin 
 1 
sin  r
na cos 
 sin  r  cos    r  90    30
quindi:
  180  120   r  30   i  90    60
Quindi, dalla condizione di angolo limite:
sin  i  sin  c 
n2
n1
 n2  n1sin  i  1.50
Invece nel caso b) dalla condizione di angolo limite:
sin  i  sin  c 
n2
n1
 n2  n1sin  i  1.50
2)
f' 
nx R
nR
 x
 2R
nx  n1
nx  1
s'  f '
m
I 0  A  I1  y'
2
da cui: nx = 2
n1s '
 - 1.33 10-12
nx s
 I1  722 kW/m 2
3)
1
n n  1
1  1.66  1  1 1 
-1
 
 1 2  
      0.039 cm
f
n2  R1 R 2 
1  7 12 
da cui :
f   25.1 cm
1
1
1


s
s'
f
m  
 s' 
f s
  4.17 cm
s f
s'
 0.83
s
Immagine virtuale, rimpicciolita, dritta
R1
F
R2
4)
dalla legge dell'interferenza a incidenza quasi normale su lamine sottili:
λ 0 ( I max ) 
4nd
(2m  1)
L’unico valore a cadere nel visibile è:
λ 0 ( I max ) 
4nd
 387 nm
3
Corrispondente a una colorazione blu.
m  0, 1, 2, 3, .....