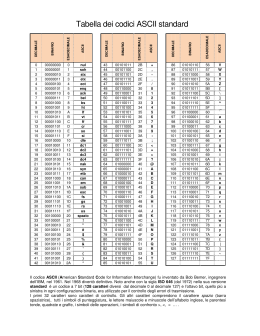
La codifica
by Vaccaro Maria Antonietta
Uno dei problemi fondamentali che incontriamo quando
vogliamo usare un sistema di calcolo per manipolare
delle informazioni é quello di rappresentare le
informazioni stesse all'interno del sistema.
Questo problema viene risolto in informatica mediante
l'adozione di oppurtuni codici che stabiliscono
una corrispondenza tra la "informazione" significativa
per il problema (l'applicazione) che si sta considerando
ed una serie di simboli manipolabili dal sistema
Elementi caratteristici di un codice
• Simboli
• Parole
• Regole di codifica
Esistono diversi tipi di codifica..
Codifica binaria
Verso la fine degli anni 30, Claude Shannon dimostrerà che con
l'aiuto dei « contrattori » (interruttori) chiusi per « vero » e aperti per «
falso » era possibile effettuare delle operazioni logiche associando il
numero 1 per « vero » e 0 per « falso ».
Questa codifica dell'informazione è detta base binaria. E' con questa
codifica che funzionano i computer.
Essa consiste nell'utilizzare due stati (rappresentati dalle cifre 0 e 1)
per codificare le informazioni.
Dal 2000 a.c. l'uomo calcola con 10 cifre (0, 1, 2, 3, 4, 5, 6, 7, 8, 9),
parlando quindi di base decimale. Tuttavia nelle civiltà più antiche o
per alcune applicazioni attuali sono state utilizzate, e lo sono ancora,
delle altre basi di calcolo :
•base sessagesimale (60), utilizzata dai Sumeri. Questa base è
ugualmente utilizzata nel sistema orario attuale, per i minuti e i
secondi;
•base vigesimale (20), utilizzato dai Maya;
•base duo decimale (12), utilizzato dagli anglosassoni nei loro sistemi
monetari fino al 1960 : un « pound » rappresentava venti « scellini »
ed uno « scellino » rappresentava dodici « pences ». Il sistema orario
attuale funziona anche su dodici ore (soprattutto nella notazione
anglosassone);
•base quinaria (5), utilizzata dai Maya;
•base binaria (2), utilizzata dall'insieme delle tecnologie digitali.
Il bit
0 0
Con un bit è quindi possibile ottenere due stati: sia 1,
sia 0. Grazie a 2 bits, è possibile ottenere quattro stati
diversi (2*2) :
Con 3 bits, è possibile ottenere otto stati diversi (2*2*2) :
Valore
binario su 3
bits
Valore decimale
000
0
001
1
010
2
011
3
100
4
101
5
110
6
111
7
0 1
1 0
1 1
Per un gruppo di n bits, è possibile
rappresentare 2n valori.
Pesi dei bits
In un numero binario, il valore di un bit, detto peso,
dipende dalla posizione del bit partendo da destra.
Come le decine, le centinaia e le migliaia per numero
decimale, il peso di un bit cresce del doppio andando da
destra verso sinistra come mostra la tabella seguente :
Numero
binario
1
Pesi
27 = 128 26 = 64 25 = 32 24 = 16 23 = 8 22 = 4 21 = 2 20 = 1
1
1
1
1
1
1
1
Conversioni
Per convertire una parola binaria in numeri decimali,
basta moltiplicare il valore di ogni bit per il suo peso,
poi sommare ogni risultato.
Così, la parola binaria 0101 vale in decimale :
23x0 + 22x1 + 21x0 + 20x1 = 8x0 + 4x1 + 2x0 + 1x1 = 5
Il byte
Il byte (in inglese byte o B in maiuscolo nelle notazioni) è un'unità d'informazione
composta da 8 bits. Permette ad esempio di stoccare un carattere, come una
lettera o una cifra.
Questo raggruppamento di numeri in serie di 8 permette una leggibilità più
estesa, nello stesso modo in cui si apprezza, in base decimale, di raggruppare i
numero a tre per poter distinguere le migliaia. Il numero « 1 256 245 » è ad
esempio più leggibile che « 1256245 ».
Un'unità d'informazione composta da 16 bits è generalmente detta parola (in
inglese word).
Un'unità d'informazione con 32 bits di lunghezza è detta parola doppia(in
inglese double word, da cui la definizione dword).
Per un byte, il numero più piccolo è 0 (rappresentato da otto zero 00000000), e il
più grande è 255 (rappresentato da otto cifre « uno » 11111111), che rappresenta
256 possibilità di valori differenti.
27 =128 26 =64 25 =32 24 =16 23 =8 22 =4 21 =2 20 =1
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
KiloBytes, MegaBytes
Da tempo l'informatica si è singola rizzata dall'utilizzo di diversi valori per le unità
del sistema internazionale. Così molti informatici hanno imparato che 1 kilobyte
valeva 1024 bytes. Ora, dal dicembre 1998, l'organismo internazionale IEC ha
istituito sulla questione (http://physics.nist.gov/cuu/Units/binary.html). Ecco le
unità standardizzate :
•Un kilobyte (ko o kB) = 1000 bytes
•Un Megabyte (Mo o Mb) = 1000 ko = 1 000 000 bytes
•Un Gigabyte (Go o Gb) = 1000 Mo = 1 000 000 000 bytes
•Un Terabyte (To) = 1000 Go = 1 000 000 000 000 bytes
Le operazioni in binario
Le operazioni aritmetiche semplici come l'addizione, la sottrazione e la
moltiplicazione sono facili da effettuare in binario.
L'addizione in binario
L'addizione in binario si fa con le stesse regole del
decimale :
Si cominciano a sommare i bit di peso minore (i
bit di destra) poi si hanno dei riporti quando la
somma dei due bit dello stesso peso sorpassa il
valore dell'unità più grande (nel caso binario: 1),
questo riporto è spostato sul bit di peso più forte
successivo...
Ad esempio :
0 1 1 0 1 +
0 1 1 1 0
______________________________
1 1 0 1 1
La moltiplicazione in binario
0x0=0
La moltiplicazione si effettua
formando un prodotto
0x1=0
parziale per ogni digit del
1x0=0
moltiplicatore (solo i bit non
1x1=1
nulli daranno un risultato
non nullo). Quando il bit del
moltiplicatore è nullo, il
moltiplicatore
prodotto parziale è nullo,
quando vale uno, il prodotto
parziale è costituito dal
moltiplicando
moltiplicando spostato dal
numero di posizioni uguale
0
al peso del bit del
0
0
moltiplicatore.
Ad esempio :
0
1
0
0
0
0
1
1
0
0
0
x
0
0
1
0
risultato
LA SOTTRAZIONE
Si cominciano a sottrarre i bit di
peso minore (i bit di destra) poi
si gestiscono i prestiti
secondo le normali regole)
Ad esempio : Le regole della
sottrazione di due bit sono
sintetizzate nella seguente
tabella:
0-0 = 0
1-1 = 0
1-0 = 1
0-1 = 1 con prestito di 1
1
1
1
0
1
0
1
1
1
0
-
_____________________________________________________
0
0
1
1
1
La divisione
Procedimento dell'operazione:
si cerca la prima parte del dividendo che sia
maggiore del divisore. si scrivere 1 al quoziente,
calcolando il resto come differenza binaria. A
questo punto "si abbassa" la cifra successiva del
dividendo e si scrive 1 se il dividendo è
maggiore del divisore, altrimenti si scrive 0 e si
abbassa una nuova cifra.
L'operazione termina quando non ci sono più cifre
da calare esempio:
10010110:1100=1100 con resto 110