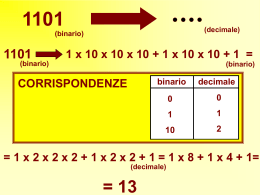
Corso di Introduzione all’Informatica Conversione Decimale Binario Esercitatore: Fabio Palopoli Conversione decimale - binario 1 Convertire il numero decimale 11110 (111 decimale) in binario. 11110 : 210 = 5510 resto 1 (bit meno significativo) 5510 : 210 = 2710 resto 1 2710 : 210 = 1310 resto 1 1310 : 210 = 610 resto 1 610 : 210 = 310 resto 0 310 : 210 = 110 resto 1 110 : 210 = 010 resto 1 (bit più significativo) Quindi 11110 è equivalente a 11011112. 2 Convertire il numero 321 (decimale) in binario 321 : 2 = 160 resto 1 160 : 2= 80 resto 0 80 : 2 = 40 resto 0 40: 2 = 20 resto 0 20: 2 = 10 resto 0 10: 2 = 5 resto 0 5: 2 = 2 resto 1 2: 2 = 1 resto 0 1: 2 = 0 resto 1 Quindi il numero 321 (decimale) è equivalente a 101000001 (binario). 3 CODIFICA DEI NUMERI INTERI Modulo e segno Il bit più a sinistra rappresenta il segno del numero (0 = ‘+’ , 1 = ‘-’) Esempio: +7 = 0111, -7 = 1111 Valori da -2k-1+1 a 2k-1-1 Con k=4 bit: da -23+1=-7 a 23-1=+7 Attenzione ci sono due zeri! +0=0000 e -0=1000 4 CODIFICA DEI NUMERI INTERI Complemento a 2 5 CODIFICA DEI NUMERI INTERI – Complemento a 2 6 Complemento a 2 Convertire il numero -13 (decimale) in complemento a due a 8 bit. Converti 13 in binario senza segno Æ 1101 Converti +13 in binario (modulo e segno) Æ 01101 Rappresenta +13 in binario (modulo e segno) a 8 bit Æ 00001101 b) Inverti i bitÆ11110010 c) Somma 1Æ11110010+00000001 = 11110011C2 7 Interpretare la traccia Convertire in binario ad 8 bit (rappresentazione in complemento a due) il numero relativo –N, dove N è ottenuto moltiplicando le ultime due cifre del proprio numero di matricola M (eventuali cifre “0” devono essere sostituite da cifre “9”). Ad esempio M10 = 33440, N10 = 4·9 = 36, –N10 = –36 Æ –NC2 = ?. 8 Convertire il numero -27710 in complemento a 2 (10 bit) Tramite algoritmo divisioni successive trovo: 277 = 100010101 Aggiungo il segno: +277 = (0) 100010101 -277 = 1011101010 + 0000000001 = 1011101011 9
Scaricare