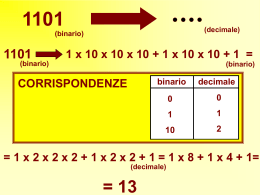
Rappresentazione dei dati
Rappresentazione digitale
dei dati
Numeri interi
Numeri reali
Caratteri
Memoria del
calcolatore è finita
(C++: int)
(C++ float e double)
(C++ char)
L’insieme dei
numeri (interi e
reali) e dei caratteri
rappresentabili è
finito
Gli interi nel computer
Con 32 bit rappresento 232 numeri distinti.
Con n bit bn-1…b1 b0:
20 21 22
2n-3 2n-2 2n-1
b0 b1 b2
bn-3 bn-2 bn-1
x  bn1 2
n 1
   b1 2  b0 2  i 0 bi 2
1
0
e i negativi ?
n 1
i
Gli interi nel computer
+/- 20 21
2n-3 2n-2 2n-1
s b0 b1
bn-3 bn-2 bn-1
Riserviamo il primo bit per il segno:
0 = positivo
1 = negativo.
I numeri positivi rappresentabili sono
quelli compresi tra 0 e 2n-1-1
Complemento a uno
Si complementa a 2n-1 il valore assoluto
del numero.
x
2  i 0 bi 2  i 0 (1  bi )2
n 1 i
i 0
n 1
i
n 1
i
Rappresentazione dello 0
630=
--63
in binario
111111000000=
------111111
Con n = 6 si rappresentano i numeri:
Rappr.
0
1 ...
31
32 ...
63
Numero
0
1 ... 31
positivi
-31 ...
negativi
-0
Esempio
Esempio con n = 6 bit: la rappresentazione di –10 è:
6310=
--53
in binario
111111001010=
------110101
Complemento a due
Si complementa il valore assoluto del
numero a 2n invece che a 2n-1.
Esempio con n = 6 bit: la rappresentazione
di –10 è:
6410=
--54
in binario
1000000001010=
------0110110
Rappresentazione dello 0
Complementando 0 si ottiene ancora 0
in binario
640=
--64 ha gli ultimi 6 bit uguali a 0
1000000000000=
------1000000
Esempio
Complementando 54 (che rappresenta –10)
si ottiene
64in binario
54=
--10 ha il bit 6 uguale a 0(positivo)
1000000110110=
------0001010
Esempio
Complementando 32 (che rappresenta –32)
si ottiene
64in binario
32=
--32 ha il bit 6 uguale a 1(negativo)
1000000100000=
------0100000
Interi in complemento a due
Con n = 6 si rappresentano i numeri:
Rappr.
0
1 ...
31
32 ...
63
Numero
0
1 ... 31
positivi
-32 ...
negativi
-1
In generale: con n bits
positivi
negativi
0 .... 2n-1-1
-2n-1 .... -1
Somma
Somma di numeri positivi: 10+12
decimale
10+
12=
--22
binario
riporto 001000
001010+
001100=
------0010110
Somma di numeri negativi
Somma di numeri negativi: (-10)+(-12)
-10  64-10 = 54
decimale
54+
52=
--106
-12  64-12 = 52
binario
110110+
110100=
------1101010
Somma di numeri negativi
106-64=42
64-42 = 22
bit di overflow
complemento
-22  64-22= 42
verifica
1101010
0*25+1*24+0*23+1*22+0*20
- 22
Somma
Somma con un numero negativo (-10)+12
-10  64-10 = 54
decimale
54+
12=
--66
binario
110110+
001100=
------1000010
Overflow
27+
12=
--39
64-39 = 25
011011+
001100=
------0100111
-25  64-25= 39
Risultato: 27+12 = -25
Overflow
-27  64-27= 37
37+
52=
--89
-12  64-12= 52
100101+
110100=
------1011001
89-64 = 25
Risultato: -27-12 = 25
Rappresentazione decimale e
binaria dei razionali
5
4
in binario
101
100
5 : 4 = 1,25
10
20
parte
0
1,2510
intera
decimale
101 : 100 = 1,01
100
0
parte
intera
binaria
parte
frazionaria
decimale
1,012
parte
frazionaria
binaria
Esempio 1
7
3
7 : 3 = 2,33..
10
10
1
2,333..10
=
2,310
in binario
111
11
111 : 11 = 10,01001001..
0100
100
100
10,0100100..2
=
10,0102
Esempio 2
7 : 5 = 1,4
20
0
7
5
1,410
in binario
111
101
111 : 101 = 1,0110001000..
1000
110
1000
1,0110001000..2
110
1000
=
1,0110002
Irrazionali

3,141592....10
in binario

?
Parte frazionaria
0,1101001
2-1+ 2-2 + 2-4 + 2-7
Trucco
moltiplicare per 2 significa spostare la
virgola di un posto a destra
0,1101001
2-1 2-2...
1,101001
20 2-1.......
Esempio 1
0,99 (decimale) = 0,b1b2b3...bk (binario)
allora 2 0,99 = 1,98 = b1,b2b3...bk
quindi b1 è 1
e 0,98 è rappresentato da 0,b2b3...bk
Esempio 2
rappresentazione binaria di
0,592= 1,18
0,182= 0,36
0,362= 0,72
0,59
0,722= 1,44
0,442= 0,88
0,882= 1,76
0,100101...
Rappresentazione dei reali
1
8
23
s e+127
m
Rappresenta:
x=s
e
2 ·
1,m
implicito
Estensione dei numeri in
virgola mobile
0 e 255 sono esponenti riservati:
1  e+127  254
quindi
-126  e  127
Esempio
12,65  1100, 101001...
???
0,652 = 1.30
0,302 = 0.60
0,602 = 1.20
0,202 = 0.40
0,402 = 0.80
0,802 = 1.60
…..
Esempio cont.
1100,101001... = 23  1,100101001...
mantissa = 1,100101001...
esponente 3 e quindi 3+127 = 130
esponente = 10000010
segno = 0
0 10000010 100101001...
Rappresentazione dei Reali
“piccoli”
1
8
s
0
23
m
Rappresenta:
x=s
-126
2 0,m
implicito
0  0,m < 1
quindi
-2-126 < x < 2-126
Rappresentazione dei Reali
“grandi”
1
8
23
s 255
Rappresenta:
0

Si può ottenere come risultato di qualche
operazione aritmetica (es: divisione per 0).
Se lo si usa come operando in una
operazione aritmetica si ha un errore.
quanti reali si rappresentano?
con una parola, cioè 32 bits possiamo
rappresentare 232 cose, quindi al più 232
reali, la novità è che questi valori non sono
distribuiti uniformemente come gli interi
ma sono maggiormente concentrati in
vicinanza dello 0 e si diradano sempre più
allontanandosi dallo 0.
Distribuzione disuniforme
h=2 bits di mantissa e k=3 di esponente.
k 1
e

2
1  e  3
Rappresentazione dell’esponente:
0
0
0
0
0
0
0
0
0
0
0
0
000
000
000
000
001
001
001
001
010
010
010
010
00
01
10
11
00
01
10
11
00
01
10
11
=
=
=
=
=
=
=
=
=
=
=
=
0
2-2
2-2
2-2
2-2
2-2
2-2
2-2
2-1
2-1
2-1
2-1
=
·2-2
=
·2-1
=
·(2-1 +2-2 )
=
·1 = 4/32
=
·(1+2-2 )
=
·(1+2-1)
=
·(1+2-1 +2-2 ) =
·1
=
·(1+2-2 )
=
·(1+2-1)
=
·(1+2-1 +2-2 ) =
0
0.0625
0,125
0,1875
0,25
0,3125
0,375
0,4375
0,5
0,625
0,75
0,875
Distribuzione disuniforme cont.
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
011
011
011
011
100
100
100
100
101
101
101
101
110
110
110
110
111
00
01
10
11
00
01
10
11
00
01
10
11
00
01
10
11
00
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
20
20
20
20
21
21
21
21
22
22
22
22
23
23
23
23

·1
·(1+2-2 )
·(1+2-1)
·(1+2-1 +2-2
·1
·(1+2-2 )
·(1+2-1)
·(1+2-1 +2-2
·1 = 4
·(1+2-2 )
·(1+2-1)
·(1+2-1 +2-2
·1
·(1+2-2 )
·(1+2-1)
·(1+2-1 +2-2
)
)
)
)
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
1
1,25
1,5
1,75
2
2,5
3
3,5
4
5
6
7
8
10
12
14

Distribuzione disuniforme cont.
4
8
0,5
0
2
0,25
1
0,125
0
10
1
12
14
