Il linguaggio dei computer:
rappresentazione in binario e algoritmi di
conversione
25 settembre 2015 ore 9-12
Libri di testo
I libri di testo sono:
• [PH] D. A. Patterson , J. L. Hennessy, “Struttura e progetto dei
calcolatori”, IV ed., 2014, Zanichelli, ISBN: 978-88-08-35202-6
(parte dei primi 5 capitoli e Appendice B online)
Va bene anche la III ed. col CD
• [P] F. Preparata, “Introduzione alla
organizzazione e progettazione di un
elaboratore elettronico”, Ed. Franco Angeli
2012, ISBN: 9788820474157 (parte dei
capp. 1 e 4)
Il linguaggio dei computer
Linguaggio dei computer
I computer «parlano» in binario:
Spento, acceso (dei circuiti elettrici)
ON, OFF
1,
0 bit = binary digit
Rappresentazione in binario
Cosa possiamo rappresentare in binario?
Numeri (interi, col segno, con la virgola)
Parole (codificando le lettere)
Istruzioni
Programma
«Informazione»
Idea fondamentale su cui sono costruiti i calcolatori:
programmi e dati rappresentati da numeri
Rappresentazione in binario
Quali/ quanti interi posso rappresentare con una sequenza di n bit?
n=1
0
1
n=2
n=3
0
0
1
1
0 00 = 0
0 01 = 1
0 10 = 2
0 11 = 3
1 00 = 4
1 01 = 5
1 10 = 6
1 11 = 7
0=0
1=1
0=2
1=3
n=4
0 000 = 0
0 001 = 1
0 010 = 2
0 011
0 100 .
0 101 .
0 110 .
0 111 .
1 000 .
1 001 .
.
1 010
1 011
1 100
1 101 = 13
1 110 = 14
1 111 = 15
Rappresentazione con n bit
Con n bit è possibile rappresentare
tutti i 2n interi compresi fra 0 e 2n-1
Perché?
Prova
Se con k bit posso rappresentare p sequenze distinte,
con k+1 bit posso rappresentare 2p sequenze distinte
1 bit
2 bit
3 bit
2 sequenze distinte
4 sequenze distinte
8 sequenze distinte
4 bit
16 sequenze distinte
.
.
.
k bit
.
.
.
2k sequenze distinte
Si formalizza con una prova per induzione.
Rappresentazione in binario
n=1
0
1
n=2
n=3
0
0
1
1
0 00 = 0
0 01 = 1
0 10 = 2
0 11 = 3
1 00 = 4
1 01 = 5
1 10 = 6
1 11 = 7
0=0
1=1
0=2
1=3
Ma perché 101 in binario rappresenta 5
e 1101 = 13?
n=4
0 000 = 0
0 001 = 1
0 010 = 2
0 011
0 100 .
0 101 .
0 110 .
0 111 .
1 000 .
1 001 .
.
1 010
1 011
1 100
1 101 = 13
1 110 = 14
1 111 = 15
Notazione decimale
… o notazione araba:
7 5 2 = 7  102 + 5  101 + 2  100
Ogni cifra ha un peso diverso secondo la posizione
che occupa:
7 centinaia
5 decine
2 unità
E’ una notazione posizionale
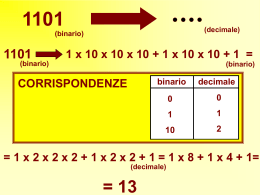
Notazione binaria
1 0 1 = 1  22 + 0  21 + 1  20 = 5
1 1 0 1 = 1  23 +1  22 + 0  21 + 1  20 = 13
Ogni cifra ha un peso diverso secondo la
posizione che occupa
E’ una notazione posizionale
Ambiguità
Per distinguere le due rappresentazioni:
(101)2 = (5) 10
(1101)2 = (13) 10
Da binario a decimale
N = (10110101)2
N = 1  27 + 0  26 + 1  25 + 1  24 + 0  23 + 1  22 + 0  21 + 1  20
N  2 7  25  2 4  2 2  2 0 
 128  32  16  4  1  181
Da decimale in binario
N = (181)10
Cerco la più grande potenza di 2 contenuta in 181:
181 = 128 + 53 = 27 + 53
53 = 32 + 21 = 25 + 21
21 = 16 + 5 = 24 + 5
5 = 4+1 = 22+1
1 = 20
181 = 27+ 25+24 +22 + 20
20=1
21=2
22=4
23=8
24=16
25=32
26=64
27=128
28=256
181 = (10110101) 2
Nota: esiste un unico modo di esprimere un intero come somma di
potenze di 2
Vedremo altri «algoritmi» per i passaggi da decimale in binario e
viceversa
Notazione posizionale (in base 8)
La notazione posizionale è definita solo per 2 e 10?
Potremmo definirla per 8?
(1 0 1) 10 = 1  102 + 0  101 + 1  100
(1 0 1) 2 = 1  22 + 0  21 + 1  20 = (5) 10
(1 0 1) 8 = 1  82 + 0  81 + 1  80 = ( 65 ) 10
(1 1 0 1) 10 = 1  103 + 1  102 + 0  101 + 1  100
(1 1 0 1) 2 = 1  23 +1  22 + 0  21 + 1  20 = (13) 10
(1 1 0 1) 8 = 1  83 +1  82 + 0  81 + 1  80 = ( 577 ) 10
Notazione binaria per numeri naturali
In base 2.
I simboli ammessi sono 0,1.
Una sequenza / stringa di 0 e 1, di lunghezza n
an-1 an-2 …a1 a0
con ai  {0, 1} per i = 0, 1, …, n-1
rappresenta l’intero N:
N = (an-1 an-2 … a1 a0 )2 =
= an-1  2n-1 + an-2 2n-2 + … + a1 21 + a0 20
In notazione compatta:
n 1
i
N   ai 2
i 0
Notazione posizionale (in base b generica)
In base b.
I simboli ammessi sono 0,1, … , b-1.
Una sequenza / stringa di 0, 1, … , b-1, di lunghezza n
an-1 an-2 …a1 a0
con ai  {0, 1, … , b-1} per i = 0, 1, …, n-1
rappresenta l’intero N:
N = (an-1 an-2 … a1 a0 )b =
= an-1  bn-1 + an-2 bn-2 + … + a1 b1 + a0 b0
n 1
In notazione compatta:
i
N   ai b
i 0
Esempi
(234)10
2  102  3  10  4  23410
(234)8
2  82  3  8  4  15610
(234)16
2  162  3  16  4  56410
(101)10
1  102  0  10  1  10110
(101)8
1  82  0  8  1  6510
(101)2
1  22  0  2  1  510
Esercizio
• Da cosa sono caratterizzati i numeri pari in binario?
(11010)2 è pari?
• Dimostrare nel modo più formale, preciso e convincente
la vostra affermazione.
Algoritmi di conversione binario
decimale
• Da binario a decimale: moltiplico ogni cifra per
l’opportuna potenza di 2 e poi sommo
• Da decimale a binario: esprimo il numero come
somma di potenze di 2, partendo dalla più grande
potenza di 2 minore del numero
Esistono altri «algoritmi» per convertire un numero dalla
rappresentazione binaria alla decimale e viceversa
Bisogna conoscere più metodi di soluzione! Per scegliere il
più adatto, veloce, …. Mai accontentarsi!
Verso un algoritmo di conversione (b=10)
b = 10
N = (3752) 10
n=4
(3 7 5 2) 10 = 3  103 + 7  102 + 5  101 + 2  100
oppure lo possiamo ottenere così:
Idea:
3
3  10 + 7 = 37
37  10 + 5 = 375
375  10 + 2 = 3752
S3 =
S2 =
S1 =
S0 =
3
37
375
3752 = N
3752
3 7 52
3752
3752
3 7 5 2 = 3  103 + 7  102 + 5  10 + 2 =
= (3  102 + 7  10 + 5 )  10 + 2 =
= ( (3  10 + 7)  10 + 5 )  10 + 2 =
= ( ( (3)  10 + 7)  10 + 5 )  10 + 2
Verso un algoritmo di conversione (b=2)
b=2
N = (1101) 2
n=4
(1 1 0 1) 2 = 1  23 + 1  22 + 0  21 + 1  20
oppure lo possiamo ottenere così:
Idea:
1
12+1=3
32+0=6
6  2 + 1 = 13
S3 =
S2 =
S1 =
S0 =
1
3
6
13 = N
1101
1101
1101
1101
1 1 0 1 = 1  23 + 1  22 + 0  2 + 1 =
= (1  22 + 1  2+ 0 )  2 + 1 =
= ( (1  2 + 1)  2 + 0 )  2 + 1 =
= ( ( (1)  2 + 1)  2 + 0 )  2 + 1
Verso un algoritmo di conversione (da b=2)
N = (an-1 an-2…a1a0)2
N = an-12n-1+ an-22n-2+ …+ a12+ a0
= (an-12n-2+ an-22n-3+ …+ a22 + a1) 2 + a0
S0 = S1 2 + a0
= ( (an-12n-3+ an-22n-4+ …+ a2) 2 + a1) 2 + a0
S1 = S2 2 + a1
…..
…..
= ((… (an-12+ an-2) 2 + … + a2) 2 + a1)2 + a0
= ((… ( (an-1) 2+ an-2) 2 + … + a2) 2 + a1)2 + a0
S2 = S3 2 + a2
…..
Sn-2 = Sn-1 2 + an-2
Sn-1 = an-1
Algoritmo di conversione: binario in decimale
MSD=cifra più significativa
N = (an-1 an-2…a1a0)2
LSD=cifra meno significativa
N = ((… ( ( an-1) 2+ an-2) 2 + … + a2) 2 + a1)2 + a0
S0 = S1 2 + a0
S1 = S2 2 + a1
S2 = S3 2 + a2
…..
Sn-2 = Sn-1 2 + an-2
Sn-1 = an-1
Dal
basso
verso
l’alto:
da an-1
a a0 ;
da MSD
a LSD
Sn-1 = an-1
Sn-2 = an-2 + 2Sn-1
Sn-3 = an-3 + 2Sn-2
…..
Si = ai + 2Si+1
…..
S0 = a0+2S1
S0 =N
Sn-1 = an-1
Sn-2 = an-2+2Sn-1
Sn-3 = an-3+2Sn-2
…..
Si = ai+2Si+1
…..
S0 =N
Esempio 1
N = (a7 a6 a5 a4 a3 a2 a1a0)2
(1 0 1 1 0 1 0 1)2
S7 = a7 = 1
S6 = a6+2S7 = 0 + 2 = 2
S5 = a5+2S6 = 1 + 4 = 5
S4 = a4+2S5 = 1 + 10 = 11
S3 = a3+2S4 = 0 + 22 = 22
S2 = a2+2S3 = 1 + 44 = 45
S1 = a1+2S2 = 0 + 90 = 90
S0 = a0+2S1 = 1 + 180 = 181
n=8
Esempio 2
(11101001)2
n=8
S7 = a7 = 1
S6 = a6+2S7 = 1 + 2 = 3
S5 = a5+2S6 = 1 + 6 = 7
S4 = a4+2S5 = 0 + 14 = 14
S3 = a3+2S4 = 1 + 28 = 29
S2 = a2+2S3 = 0 + 58 = 58
S1 = a1+2S2 = 0 + 116 = 116
S0 = a0+2S1 = 1 + 232 = 233
Esempio 3
(11111111)2
n=8
S7 = a7 = 1
S6 = a6+2S7 = 1 + 2 = 3
S5 = a5+2S6 = 1 + 6 = 7
S4 = a4+2S5 = 1 + 14 = 15
S3 = a3+2S4 = 1 + 30 = 31
S2 = a2+2S3 = 1 + 62 = 63
S1 = a1+2S2 = 1 + 126 = 127
S0 = a0+2S1 = 1 + 254 = 255
Algoritmo di conversione: decimale in binario
N = (an-1 an-2…a1a0 )2
Dato N trovare an-1 , an-2 , …, a1 , a0 con ai = 0 o 1
Procedura inversa: dall’alto verso il basso da a0 ad an-1;
da LSD a MSD
a0 ed S1 sono rispettivamente il resto e il
N= S0 = S1 2 +a0
quoziente della divisione di N= S0 per 2.
S1 = S2 2 + a1
S2 = S3 2 + a2
……
Si = Si+1 2 + ai
……
Sn-2 = Sn-1 2 + an-2
Sn-1 = an-1
….
ai ed Si+1 sono rispettivamente il resto e
il quoziente della divisione di Si per 2.
….
Fino ad ottenere un Si =0.
Algoritmo delle divisioni successive
Esempio 1 (decimale in binario)
N=152
S0 = N = a0+2 S1
S1 = a1 + 2 S2
S2 = a2 + 2 S3
…..
Si = ai + 2 Si+1
…..
Sn-1 = an-1
N = (an-1 an-2…a1a0)2
S0 = a0+2S1 = 0 + 276 = 152
S1 = a1+2S2 = 0 + 2  38 = 76
S2 = a2+2S3 = 0 + 2  19 = 38
S3 = a3+2S4 = 1 + 2  9 = 19
S4 = a4+2S5 = 1 + 2  4 = 9
S5 = a5+2S6 = 0 + 2  2 = 4
152 : 2 = 76 con resto 0
S6 = a6+2S7 = 0 + 2  1 = 2
2 : 2 = 1 con resto 0
S7 = a7+2S8 = 1 + 2  0 =1
1 : 2 = 0 con resto 1
N = (10011000)2
76 : 2 = 38 con resto 0
38 : 2 = 19 con resto 0
19 : 2 = 9 con resto 1
9 : 2 = 4 con resto 1
4 : 2 = 2 con resto 0
STOP
Conversione da decimale a base B
Numero di bit per rappresentare N
E’ possibile prevedere il numero di bit necessari per rappresentare N in binario?
Potevamo prevedere che per rappresentare N = 152 occorrevano 8 bit?
E’ possibile rappresentare 152 con 7 bit?
No , perché con 7 bit possiamo rappresentare tutti e soli gli interi da 0 a 27 - 1=127
E’ possibile rappresentare 152 con 8 bit?
Si, perché con 8 bit possiamo rappresentare tutti gli interi da 0 a 28 - 1 = 255
In effetti: 27-1< 152 <= 28-1.
Il minimo numero di bit necessari a rappresentare N in binario lo ottengo
considerando log 2 N e arrotondandolo al più piccolo intero superiore.
log 2 152 = 7,…. che arrotondato superiormente da 8.
Nota: 152 si può rappresentare anche con 9, 10, 11, ….. bit:
(152)10 = (10011000)2 = (010011000)2 = (0010011000)2 = (00010011000)2
Riepilogo
• Rappresentazione binaria con n bit
• Algoritmi di conversione bin->dec e dec->bin
[P] parr. 1.1, 1.2, 1.3.1