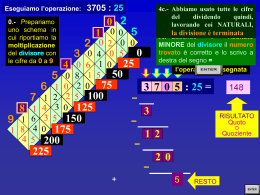
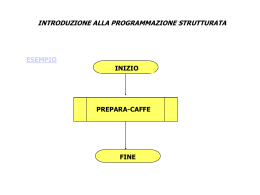
Divisione Tradizionale
 Divisione con Ruffini
DIVISIONE
TRADIZIONALE
Introduzione
(dividendo)
19:3= 6(quoziente)
(divisore)
N= dividendo
D= divisore
Q= quoziente
1= resto
R=resto
0rd
N:D=Q
N=DxQ+R
P(x)=(x4+3x2-4x+5) : (x-1)
D(x)=(x-1)
Q(x)=?
R(x)=?
(x4+0+3x2-4x+5)
(x-1)
-x4+x3
// +x3+3x2-4x+5
x3
// 4x2-4x+5
-4x2+4x
// // 5
resto
X3+x2
X3+x2+4x
X3+x2+4x
Q(x)
1) Ordinare il polinomio secondo
le potenze decrescenti della
variabile che lo identifica,
mettendo eventuali zeri nelle
potenze mancanti.
2) Fare la stessa cosa per il
divisore; non serve mettere gli
zeri eventuali.
3) Dividere il monomio di
grado massimo del
dividendo per il monomio di
grado massimo del
divisore; scrivere il
monomio
ottenuto
4) Si moltiplica
il sotto al
divisore
monomio ottenuto per
tutto il divisore scrivendo
il polinomio che si ottiene
cambiato di segno e
incolonnato sotto al
dividendo
rispettando
le
5) Sommare
i due polinomi
a sinistra
potenze
6) Si rifà la stessa cosa dal
punto 3 fino a quando il grado
del polinomio dividendo
parziale è maggiore o uguale
del divisore.
home
DIVISIONE CON
LA REGOLA DI
RUFFINI
Il grado del resto deve essere minore del grado del
divisore
P(x)= D(x)
Q(x)+R(x)
Q(x)= x3+x2+4x
R(x)=5
(x-1)(x3+x2+4x)+5
X4+x3+4x2-x3-x2-4x+5
X4+3x2-4x+5
P(x)
P(x)= 6 x3+4x2-3x-7
Cambiare il
segno
D(x) = x-1
6
4
-3
+
-7
+
+
6 10 7
=
= == =
=
6 10 7 0
+1
x
!. Ha senso applicare la
regola di Ruffini solo se il
divisore è di primo grado
rispetto alla variabile di
lavoro
2. Se il divisore è di primo
grado allora il resto sarà
di grado zero (rispetto
alla variabile di lavoro)
Q(x)=6x2+10x+7
home