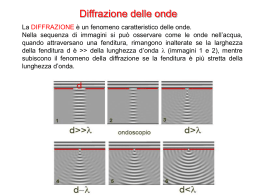
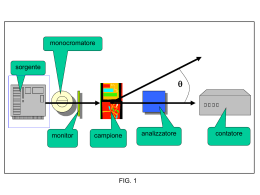
Fenomeni luminosi
Verso un nuovo modello della luce
1) Crisi della propagazione rettilinea della luce
Esperienze condotte in passato ci hanno indicato che la luce viaggia generalmente secondo linee rette!
Tuttavia è facile trovare qualche eccezione a questa regola:
a) Prendiamo:
- un laser seguito da una lente cilindrica (in modo da aumentare la dimensione del fascio laser in 1 sola
direzione, quella orizzontale); la lente non è indispensabile, ma ci aiuta a vedere meglio gli effetti a cui
siamo interessati.
- una fessura rettangolare di dimensioni molto più piccole rispetto agli oggetti considerati in passato
(larghezza inferiore a 1-2 mm), ed interponiamola sul cammino del fascio luminoso (la fenditura è
orizzontale);
osserviamo poi la sua proiezione su uno schermo a circa 3 m di distanza. La fenditura di cui disponiamo è
composta da due lamine, la cui distanza può essere modificata ruotando una rotella.
In assenza di fenditura la dimensione verticale del fascio laser sullo schermo di osservazione è di circa 3
mm.
Inseriamo la fenditura sul cammino del fascio laser:
Fenditura da 0,8 mm: sullo schermo di osservazioni si vede una zona luminosa di dimensioni orizzontali
invariate, ma di dimensioni verticali lievemente più grandi rispetto a quelle del fascio indisturbato (circa 5
mm); l’effetto più evidente è la comparsa di strisce // di luce e buio al di sopra e al di sotto della zona
centrale più luminosa
Riduciamo la larghezza della fenditura (a = 0,4 mm Æ 0, 15 mm): sullo schermo di osservazioni si vede
che le dimensioni orizzontali della zona luminosa sono ancora invariate, ma la dimensioni verticali
aumentano sempre di più man mano che la fenditura viene resa più stretta. La luce sembra quindi
incurvarsi sempre più man mano che attraversa fenditure sempre più strette. Non solo la zona centrale più
luminosa diventa sempre più larga, ma anche le strisce // di luce e buio al di sopra e al di sotto di essa si
allargano: la luce, sebbene meno intensa, raggiunge zone molto lontane dal centro della proiezione
geometrica della fenditura e per di più sembra “evitare” di propagarsi in alcune direzioni ben precise (le
strisce buie!).
fenditura da: 0,8 mm
0,4 mm
0,2 mm
0,15 mm
b) Sostituiamo ora la maschera con 1 fenditura con una maschera composta da 2 fenditure affiancate,
identiche alla precedente, ciascuna ha larghezza a = 0.15 mm, e la distanza tra i centri è d = 0.5 mm.
Nella zona centrale che prima era uniformemente illuminata compaiono fitte striscette chiare e scure. Vediamo
anche cosa accade se riduciamo la distanza tra le fenditure: ora d = 0.25 mm. La zona centrale più luminosa
continua a non cambiare né dimensione né posizione, ma le fitte striscette di luce e buio diventano sempre più
larghe man mano che le fenditure si avvicinano (ovvero man mano che la larghezza della zona nera TRA le due
fenditure diventa più piccola).
Singola: a = 0,15 mm
Doppie: a = 0,15 mm, d = 0, 5 mm
a = 0,15 mm, d = 0,25 mm
Coprendo una delle due fenditure riotteniamo la stessa identica figura che avevamo con la singola
fenditura: chi guarda lo schermo di osservazione non è in grado di dire se la fenditura coperta è quella di in
alto o i basso, in quanto la figura prodotta da una è identica a quella prodotta dall’altra (la proiezione non si
sposta né in alto né in basso)! La zona nera che separa le due fenditure non sembra quindi giocare alcun
ruolo.
Ricapitolando:
Il piegarsi della luce nell’oltrepassare ostacoli (quali i bordi della fenditura) è noto col nome di DIFFRAZIONE.
La proiezione formata dalla luce nell’attraversare piccole fenditure (o fori) è caratterizzata da una zona centrale
molto luminosa di dimensioni molto grandi rispetto alla proiezione geometrica della fenditura; notiamo inoltre la
mancanza di una netta definizione degli orli: al di là degli “orli” della zona più luminosa si vedono una serie di
strisce alternate di luce e buio. La luce si è quindi ridistribuita nello spazio, arrivando a raggiunge zone molto
lontane dalla semplice proiezione geometrica della fenditura. Questi effetti sono causati dalla diffrazione della luce.
Il piegamento è spesso così piccolo che nella maggior parte dei casi è insignificante a confronto
dell’intera immagine luminosa, non lo si nota e può quindi essere trascurato. L’affermazione secondo
cui il cammino della luce è rettilineo costituisce perciò una prima approssimazione nel descrivere
il comportamento della luce.
TUTTAVIA i fenomeni appena osservati (luce che attraversa singole fessure di dimensioni < 1mm)
non sono più spiegabili con il MODELLO A RAGGI. Abbiamo visto infatti che quando la luce
attraversa 2 fenditure // molto vicine tra loro (d < 1mm), oltre a “piegarsi” come faceva nel caso di una
singola fenditura, si ridistribuisce in maniera ancora più complicata nello spazio, creando striscette di
luce e buio alternate là dove prima l’illuminazione era uniforme; addirittura, all’interno della
proiezione geometrica delle due fenditure, si osservano molte zone in cui la luce non arriva mai
(striscette buie)!
L’asserzione che la luce si propaga in linea retta spiega dunque molti fatti, ma non sempre può essere accettata
come del tutto vera: la luce in realtà si piega leggermente intorno agli ostacoli (bordi della fenditura) tanto più quanto gli ostacoli sono piccoli - e si ridistribuisce nello spazio in maniera sempre più complicata
man mano che il numero di ostacoli o di fenditure aumenta:
FOTO di 2 – 3 – 4 – tante fenditure (tutte di uguale larghezza a = 0,15 mm a dist.0,25)
Æ oltre a comparire massimi secondari meno intensi si nota che la luce raggiunge zone sempre più lontane!
2) Alla ricerca di un nuovo modello
A questo punto abbiamo 2 scelte possibili: o modifichiamo e miglioriamo il modello corpuscolare/meccanico della
luce in modo che esso possa spiegare i nuovi fenomeni osservati, oppure cerchiamo un nuovo modello, fondato
su concetti del tutto diversi. Seguiamo questa seconda strada.
Una teoria della luce deve innanzitutto tener conto del fatto che la luce SI PROPAGA NELLO SPAZIO.
Pertanto dobbiamo domandarci: esiste qualcosa di diverso da particelle o corpuscoli che SI SPOSTA da un
punto all’altro?
La risposta è affermativa: basta pensare a ciò che osserviamo quando lasciamo cadere un sasso in uno stagno
calmo: una PERTURBAZIONE CIRCOLARE si propaga partendo dal punto in cui è avvenuto l’URTO. A questa
perturbazione diamo il nome di ONDA.
Se osserviamo l’acqua più da vicino ci accorgiamo che mentre l’onda si propaga alla superficie, l’acqua, anche se
mossa e agitata localmente, NON AVANZA con l’onda che si propaga (basta pensare al movimento di un pezzetto
di legno o di una macchia d’olio sulla superficie dell’acqua perturbata: si spostano in su e in giù al passaggio
dell’onda, ma non si spostano con l’onda): UN’ONDA PUÒ INFATTI VIAGGIARE PER LUNGHI TRATTI, MA
QUANDO LA PERTURBAZIONE È PASSATA, OGNI GOCCIA D’ACQUA è LASCIATA NEL POSTO IN
CUI SI TROVAVA. (come ulteriori esempi di onde possiamo pensare ad una banadiera legata ad un’asta che
sventola per effetto della brezza: le increspature si propagano per tutta la lunghezza della stoffa, ma i singoli punti
della stoffa mantengono le loro posizioni dopo il passaggio dell’onda. Come l’acqua anche la stoffa resta al suo
posto dopo che le onde l’hanno attraversata).
Oltre alle onde appena viste, in cui il moto si ripete continuamente, esistono altri tipi di onde. Si pensi a ciò che
accade quando una porta viene sbattuta: la breve compressione improvvisa dell’aria del vano della porta passa
come una perturbazione attraverso la stanza, imprimendo un’improvvisa spinta ad una tendina appesa alla finestra.
Quest’onda DI BREVE DURATA è detta IMPULSO. (Altri esempi di impulsi li abbiamo quando una sfera rigida
colpisce una serie di diverse sfere rigide identiche poste in fila, una accanto all’altra, oppure quando osserviamo
una fila di macchine che ripartono allo scattare del semaforo verde; in questo ultimo caso è interessante notare che
l’impulso si propaga in direzione opposta ai veicoli.)
L’elemento comune in questi esempi è il seguente: la PERTURBAZIONE SI SPOSTA ATTRAVERSO UN
MEZZO, MA IL MEZZO NON SI SPOSTA MAI CON LA PERTURBAZIONE. Le perturbazioni che si
propagano attraverso mezzi sono ciò che chiamiamo ONDE.
Possiamo quindi rispondere alla domanda iniziale: esiste dunque qualcosa di diverso dai corpuscoli che può
muoversi da un punto ad un altro? L’onda, un qualcosa che non è di per sé una particella di materia, può
propagarsi da un luogo ad un altro!!
Applet: “come viaggia il disturbo” (onda longitudinale e trasversale)
http://fisicaondemusica.unimore.it/Cos_un_onda.html,
Applet: moto del mezzo nel caso di onde trasversali e longitudinali (in una o più dimensioni)
http://fisicaondemusica.unimore.it/Onde_trasversali_e_longitudinali.html
3) Cominciamo a studiare le onde
Ci poniamo ora una seconda domanda: le onde si comportano realmente come la luce? Per appurarlo dobbiamo
saperne di più: quando sapremo come si comportano le onde potremo paragonare il loro comportamento con ciò
che conosciamo della luce e con altro che potremo conoscere. Cominciamo quindi a studiare le onde.
a) Impulso lungo una corda:
La serie di fotografie qui accanto mostra la generazione di un impulso lungo una
molla (utilizzata al posto della corda per scopi pratici: l’impulso viaggia più
lentamente lungo una molla piuttosto che lungo una corda, ed è quindi più facile
fotografarlo ad istanti successivi).
Le fotografie sono scattate ad INTERVALLI di TEMPO UGUALI.
Dalla serie di fotografie notiamo che:
- la forma dell’onda NON CAMBIA mentre si sposta
- l’impulso percorre la stessa distanza in intervalli di tempo uguali, l’onda si
muove quindi a VELOCITA’ COSTANTE
Attaccando un nastrino in un punto della
corda/molla, ci si convince facilmente del fatto che
ciascun piccolo tratto della corda si muove, al
passaggio dell’impulso, in direzione perpendicolare
alla molla
e osservando il suo movimento capiamo in che
direzione si propaga l’impulso.
Possiamo quindi capire come si muove ogni parte
della corda istante per istante!
b) Cosa accade quando 2 onde si propagano in direzione opposta nella stessa corda? Cosa accade quando
le 2 si incontrano? SI ATTRAVERSANO O SI URTANO?
La serie di istantanee qui accanto mostra due impulsi impressi contemporaneamente agli estremi di una corda:
- i due impulsi si avvicinano propagandosi lungo la corda come se l’altro non ci fosse
- quando si incrociano i 2 impulsi si combinano e creano forme complicate,
- ma dopo essersi incrociati assumono di nuovo le forme iniziali e si muovono lungo la
corda come se nulla fosse accaduto.
LE ONDE SI ATTRAVERSANO quindi SENZA MODIFICARSI! Questa è una
PROPRIETA’ FONDAMENTALE DELLE ONDE (fenomeno molto diverso dall’urto
tra corpuscoli!)
Abbiamo appena visto che quando le onde si incrociano, la forma dell’onda
risultante è diversa dalla forma delle due onde originarie.
Possiamo però vedere che relazione esiste tra queste se:
- IMMAGINIAMO ciascuna delle onde originarie nella posizione che
occuperebbe SE FOSSE SOLA (linee tratteggiate in figura),
- e SOMMIAMO gli spostamenti dovuti alle due onde originarie (linee
verticali in figura).
Si trova che LO SPOSTAMENTO TOTALE di ciascun punto della corda
è, in ogni istante, ESATTAMENTE UGUALE ALLA SOMMA DEGLI
SPOSTAMENTI
CHE
SAREBBERO
STATI
PRODOTTI,
INDIPENDENTEMENTE, DALLE 2 SINGOLE ONDE.
Questo metodo è valido per ogni numero N>2 di onde (gli spostamenti dovuti a qualsiasi numero di onde
possono essere sommati); si tratta infatti di un principio di carattere generale, detto
“PRINCIPIO di SOVRAPPOSIZIONE”:
Per trovare in ogni istante la forma dell’onda totale (ovvero il reale
spostamento del mezzo) basta sommare in ogni punto lo spostamento
pertinente a ciascuna onda che attraversa il mezzo.
VERIFICHIAMO la validità di questo principio considerando una sua conseguenza:
immaginiamo 2 impulsi identici e simmetrici, ma invertiti, che si
propagano uno verso l’altro lungo la corda.
In base al Principio di Sovrapposizione, ci aspettiamo che esista un istante
di tempo in cui lo spostamento totale della corda è nullo!
Verifichiamo se la nostra previsione è corretta: Applet di 2 impulsi identici
e simmetrici, ma invertiti:
http://fisicaondemusica.unimore.it/Cos_un_onda.html
Abbiamo quindi scoperto che le onde passano indisturbate una attraverso l’altra e procedono come se
l’altra non esistesse … esattamente come i fasci di luce emessi da due torce!!!
Anche la riflessione e la trasmissione delle onde è molto simile alla riflessione e alla trasmissione della luce:
pensiamo ad un onda sonora impulso che si propaga verso una parete. Non appena l’onda giunge sulla parete,
essa viene in parte riflessa all’indietro (eco!) e in parte trasmessa attraverso la parete. I fasci di corpuscoli si
comportano in generale diversamente: o vengono riflessi o vengono trasmessi.
Il modello ondulatorio della luce sembra dunque più vantaggioso di quello meccanico/corpuscolare.
Riflessione per casa: Cosa vi aspettate che accada se i due impulsi sono ancora identici ed inversi, ma non simmetrici?
4) Onde sulla superficie dell’acqua (esperimenti con l’ondoscopio)
Per essere certi che la rappresentazione ondulatoria sia un modello adeguato per la luce abbiamo bisogno di poter
effettuare un confronto diretto, per esempio, con la legge di Snell (legge della rifrazione della luce) e con i
fenomeni osservati sul banco ottico (diffrazione della luce da una e due fenditure). Per fare questo ci servono delle
onde che si muovano nello spazio o almeno in un piano. Studieremo quindi le onde sulla superficie dell’acqua.
Torniamo quindi al nostro primo esempio di onda: un
sasso lasciato cadere in uno stagno genera un’onda che
si propaga sulla superficie dello stagno secondo cerchi.
Queste onde si muovono alla superficie dell’acqua e
NON SI ESTENDONO IN PROFONDITÀ in misura
apprezzabile.
Parliamo
quindi
di
ONDE
SUPERFICIALI. Le onde viste attraverso le pareti di
un acquario sono generalmente molto simili a quelle
appena citate:
Ampiezza
dell’onda
Per studiare il comportamento di questo tipo di onde useremo uno strumento, detto
ONDOSCOPIO: vaschetta con fondo di vetro illuminata dall’alto, che consente di
osservare la proiezione delle immagini delle onde su uno schermo. L’immagine si
forma perché le creste fungono da lente convergente e focalizzano la luce sullo
schermo, mentre le gole fungono da lenti divergenti e fanno quindi divergere la luce;
pertanto le creste danno luogo a strisce luminose e le gole a strisce scure.
Cominciamo a fare qualche esperimento con l’ondoscopio:
a) Fronti d’onda rettilinei e circolari
Con un barretta lunga e sottile immersa nell’acqua generiamo un “FRONTE DI ONDA RETTILINEA”:
o
il fronte d’onda avanza in modo che la CRESTA RESTI
// ALLA LINEA CHE INDICA LA SUA POSIZIONE
DI PARTENZA
o
la DISTANZA tra due linee // è misurata lunga una
perpendicolare, pertanto LA DIREZIONE DI
PROPAGAZIONE dell’onda è perpendicolare alla
cresta. Da ora in poi indicheremo sempre con una
freccia la direzione di propagazione dell’onda a fronte
rettilineo.
La freccia che indica la direzione di propagazione di un’onda è sempre perpendicolare al fronte
d’onda, e la chiamiamo RAGGIO.
I raggi associati ad un’onda rettilinea sono tutti paralleli tra di loro e perpendicolari al fronte d’onda.
Ora generiamo un’onda A FRONTE CIRCOLARE immergendo una punta nell’acqua:
o
l’onda si propaga formando un cerchio più grande,
o
NON POSSIAMO ASSOCIARE UNA DIREZIONE DEFINITA
ALL’ONDA CIRCOLARE perché ESSA SI PROPAGA IN
TUTTE LE DIREZIONI.
Fronte
circolare a
due istanti
Esaminiamo però un tratto di fronte d’onda circolare abbastanza
piccolo da poter essere considerato rettilineo: il segmento si
propaga in direzione radiale verso l’esterno del cerchio, ossia in
direzione perpendicolare alla cresta dell’onda, esattamente come
avviene per le onde rettilinee!
I raggi associati ad un’onda circolare si intersecano nel punto in
cui le onde sono generate (cioè, nella sorgente puntiforme!)
b) Onde periodiche
Generiamo ore onde a fronte rettilineo una dopo l’altra, AD UGUALI INTERVALLI di TEMPO T
i.
il generatore di onde ripete identicamente il suo moto ad ogni intervallo T, si dice che il suo moto è
PERIODOCO e l’intervallo di tempo T è detto PERIODO;
per DESCRIVERE il MOTO PERIIODICO POSSIAMO anche dire QUANTE VOLTE il MOTO SI
RIPETE nell’UNITÀ di TEMPO, diamo cioè la FREQUENZA di ripetizione (se il periodo è di un
decimo di secondo, la frequenza sarà di 10 volte al sec):
f=1/T
ii.
fissiamo ora un punto dell’ondoscopio: le onde pulsate prodotte dal generatore si muovono verso questo
punto e PASSANO PER ESSO CON LA STESSA FREQUENZA CON CUI LASCIANO LA
SORGENTE (se 10 impulsi sono emessi in 1 sec, 10 onde passano ad ogni sec):
fonda = 1 / tempo tra il passaggio di due onde successive = 1/ T = f
iii.
quando le onde si muovono la distanza tra due creste consecutive qualunque è sempre la stessa: questa
distanza è detta LUNGHEZZA D’ONDA λ.
Æ Ciò che abbiamo prodotto è un’onda periodica rettilinea!
La velocità di questa onda periodica può essere facilmente dedotta: le creste sono separate da λ e ciascuna
percorre questa distanza in un tempo T, per cui:
v = λ / T = f λ.
Questa relazione vale PER OGNI ONDA PERIODICA (l’avremmo ottenuta anche considerando ONDE
CIRCOLARI PERIODICHE: qui λ è misurata lungo il raggio ed è uguale a quella di un’onda rettilinea della
stessa frequenza f, per cui vonda circ = vonda rett ) nello stesso mezzo, qualunque sia la sua frequenza!
Per poter verificare sperimentalmente quest’ultima affermazione, misuriamo la velocità delle onde nella
vaschetta per 2-3 diversi valori della frequenza. Abbiamo però bisogno di misurare la lunghezza d’onda λ
nella maniera più accurata possibile (per esempio, misurando direttamente 5-6-7 lunghezze d’onda, se non
addirittura 10 λ). Come possiamo fare?
Immaginiamo di poter guardare l’onda periodica ad intervalli regolari di tempo, tali che Toss = T. Se ciò fosse
possibile, osserveremmo sempre la stessa configurazione in quanto ogni cresta andrebbe ad occupare
esattamente la posizione della cresta che la precede. Osserveremmo una CONFIGURAZIONE
STAZIONARIA, avremmo cioè l’impressione che l’onda non si propaghi.
L’ondoscopio è dotato di un interruttore che consente di sincronizzare la luce della lampada con la frequenza
del generatore (luce stroboscopica). L’utilizzo della luce stroboscopica è particolarmente utile quando si
vogliono effettuare misure, per esempio, di lunghezza d’onda!
MISURE:
f (1/s)
20
25
30
10 λ (cm)
41,5 ± 1,5
34,5 ± 1,5
29,5 ± 1,5
λmin (cm)
4,0
3,3
2,8
λmax (cm)
4,3
3,6
3,1
vmin (cm/s)
80
82
84
vmax (cm/s)
86
90
93
v (cm)
83 ± 3
86 ± 4
88 ± 4
I risultati ottenuti sono compatibili tra loro nei limiti dell’errore: valori di velocità compresi tra 84 ed 86
cm/s, ad esempio, sono previsti in tutti e tre i casi.
c) Riflessione delle onde
ƒ
Poniamo nella vaschetta un ostacolo rettilineo parallelo alla bacchetta che genera le onde rettilinee. Le onde
riflesse sono ancora rettilinee? In che direzione si propagano? (SINGOLO IMPULSO: si vede in che
direzione si propaga l’onda riflessa; @ 15 Hz con strobe: si vede forma dell’onda riflessa)
ƒ
Cosa vi aspettate di osservare se disponiamo l’ostacolo in modo che formi un angolo di circa 45° con il
generatore di onde rettilinee? Le onde riflesse sono ancora rettilinee? In che direzione si propagano? Æ
verifica sperimentale con singolo impulso (per vedere direzione di propagazione) e con f = 15 Hz e strobe
per vedere forma e individuare meglio direzione.
ƒ
Quale relazione pensate che esista tra l’angolo di incidenza e l’angolo di riflessione?
d) Rifrazione delle onde
Strati d’acqua di diverso spessore costituiscono mezzi diversi in
cui si possono propagare le onde. Mettiamo allora nella vaschetta
una lastra di plastica e versiamo dell’acqua nella vaschetta finché
sulla lastra si forma uno strato di liquido molto sottile (meno di 1
mm), di eguale spessore in tutti i punti della lastra stessa.
ƒ
Orientiamo la lastra parallelamente al generatore. Che cosa
osservate quando le onde generate nell’acqua profonda si
propagano in quella più bassa? Le onde si mantengono
rettilinee? In che relazione vi sembrano essere le lunghezze
d’onda nei due mezzi? E le velocità? Nel passaggio da un
mezzo all’altro, la direzione di propagazione resta la stessa o
varia?
ƒ
Ora ruotiamo la lastra in modo che il suo bordo non sia
più parallelo alle onde incidenti. Le onde rifratte sono
ancora rettilinee? Nel passaggio da un “mezzo”
all’altro, la direzione di propagazione resta la stessa o
varia? Com’è l’angolo di incidenza rispetto a quello di
rifrazione? Facciamo altre prove con angoli di
incidenza diversi.
Facendo una serie di misure troveremmo che la
relazione che lega angolo di incidenza ed angolo di
rifrazione è: sen(i) / sen(r) = λ1/ λ2 = cost (il
rapporto tra i seni degli angoli di incidenza e di
rifrazione è costante ed è proprio uguale al rapporto
tra le lunghezze d’onda nei due “mezzi”). Questa
relazione non è altro che la legge di Snell, questa volta applicata alle onde; se identifichiamo il rapporto λ1/ λ2
con l’indice di rifrazione relativo n12 ( n12 = λ1/ λ2 ) le due leggi sono identiche! Notiamo che, essendo λ1 > λ2,
si ha: n12 = λ1/ λ2 >1.
Il valore dell’indice di rifrazione relativo n12 può anche essere espresso in funzione della velocità nei due
mezzi: la velocità di propagazione di un’onda (v) è legata alla lunghezza d’onda dalla relazione: v = f λ,
possiamo quindi scrivere: λ1 = v1 / f, λ2 = v2 / f, da cui:
n12 = λ1/ λ2 = (v1 / f) / ( v2 / f) = v1 / v2
La relazione è molto simile a quella ricavata con il modello meccanico della luce, solo che ora ci aspettiamo
che la velocità nel secondo mezzo (acqua poco profonda) sia MINORE della velocità nel primo (acqua più
profonda), essendo n12 = λ1/ λ2 > 1. Le previsioni del modello meccanico e di un eventuale modello ondulatorio
della luce sono dunque in disaccordo!
Riflessione: il fenomeno della dispersione
e) Diffrazione delle onde
Cosa accade quando poniamo una fenditura lungo il cammino di un’onda rettilinea?
ƒ
Generiamo onde periodiche rettilinee di frequenza 15 Hz e poniamo
una fenditura larga 6-7 cm nell’ondoscopio. Notiamo che in questa
situazione la fenditura è circa 3-4 volte maggiore della lunghezza
d’onda. Le onde sono ancora rettilinee al di là della fenditura?
Continuano a muoversi nella direzione iniziale?
ƒ
Che cosa osservate man mano che riduciamo le dimensioni della
fenditura (lasciando fissa la lunghezza d’onda)? Le onde si
incurvano sempre più al di fuori della proiezione geometrica della
fenditura e questa curvatura aumenta al diminuire delle dimensioni
della fenditura.
ƒ
Quando le dimensioni della fenditura sono circa uguali (o anche
inferiori) alla lunghezza d’onda, l’onda che emerge dalla fenditura
assomiglia molto ad un’onda circolare: una fenditura molto
stretta, investita da un’onda rettilinea, si comporta come una
sorgente puntiforme!!
L’effetto visto è un fenomeno puramente ondulatorio, la diffrazione; esso diventa facilmente osservabile
ogni volta che un’onda incontra una fenditura o un ostacolo di dimensioni confrontabili con la sua lunghezza
d’onda.
Æ Sfruttiamo le osservazioni fatte per costruire un modello: la fenditura può essere vista come un insieme di
tante sorgenti puntiformi allineate (principio di Huygens). Usando questa idea ed il principio di
sovrapposizione si riesce a spiegare la configurazione osservata, come vedremo tra breve.
Æ Perché la luce, in molte situazioni, forma ombre nette? Per capirlo
proviamo a vedere cosa accade quando manteniamo fissa la larghezza
della fenditura e variamo la lunghezza d’onda. Partiamo da onde di
lunghezza d’onda tale che la larghezza della fenditura sia a = 3-4
lambda [f=12-15Hz] (la curvatura dell’onda dopo la fenditura è
abbastanza pronunciata). Riducendo la lunghezza d’onda [25Hz e poi
30 Hz] si osserva che la curvatura diventa sempre meno evidente. Le
foto a sinistra mostrano come tale curvatura si riduca sempre più
quanto la lunghezza d’onda è piccola (a parità di fenditura). Uno
studio quantitativo mostrerebbe che le figure osservate sono
determinate dal rapporto tra la lunghezza d’onda λ e la larghezza della
fenditura a (ovvero da a/λ) e non da a e λ separatamente! Allora
forse la luce ha lunghezza d’onda molto piccola; quanto piccola? Ci
possiamo fare un’idea ricordando che gli effetti di diffrazione ottica
sono diventati evidenti quando abbiamo usato fenditure più piccole
del mm. La luce, se è un’onda, avrà lunghezza d’onda ben al di sotto
del mm. Se è così, le ombre prodotte dalla luce quando incontra
ostacoli o fenditure di dimensioni superiori al mm non sono davvero
nette, gli effetti di curvatura ai loro bordi però sono talmente piccoli
da non essere percepiti !!
e) Interferenza delle onde
[2 sorgenti puntiformi, luce steady: frequenza 20 Hz Æ si vedono le linee nodali]
Applet per capire la formazione delle linee nodali mediante il principio di sovrapposizione:
http://www.ba.infn.it/~fisi2005/evangelista/fr3.html
Linee nodali e misura della lunghezza d’onda mediante l’interferenza
Se le onde vengono generate da S1 e da S2 in concordanza di fase la
P
situazione che si determina in P dipende unicamente dalla differenza
fra i cammini che le due onde percorrono per giungere in P.
Perché in P si abbia un nodo (interferenza distruttiva), una
cresta di un’onda deve sovrapporsi ad una gola dell’altra onda;
è facile convincersi che questo avviene quando:
PS1 – PS2 = λ/2,
oppure
R
PS1 – PS2 = 3λ/2,
e così via.
In generale, per tutti i punti Pn appartenenti all’n-esima linea
S1
S2
nodale si ha:
PnS1 – PnS2 = (2n + 1)λ/2 = (n + ½)λ,
con n = 0, 1, 2, …
Supponiamo che P sia un punto sulla n – esima linea nodale (le linee nodali vengono numerate muovendosi dal
punto medio C tra le due sorgenti verso l’esterno). Quando P è sufficientemente lontano dalle sorgenti, la differenza
delle lunghezze dei percorsi PnS1 – PnS2 può essere espressa in termini della distanza d tra le fenditure e dell’angolo
che PS1 forma con d.
P
Prendiamo P sufficientemente lontano dalle sorgenti (d <<
PS1; d << PS2). Sia PR = PS2 in modo che
S1R = PS1 – PS2
Quanto più lontano è il punto P, tanto più // risultano le linee PS1 e PS2.
Scegliamo allora solo punti P così lontani da poter considerare le linee PS1 e
PS2 parallele. In
questi casi l’angolo in R è retto e abbiamo:
S1R = PS1 – PS2 = d senθ
La condizione per i minimi PnS1 – PnS2 = (n +
½)λ diventa:
R
θ
S1
B
B
d
d senθn = (n + ½)λ
S2
B
B
xn
O
Pn
B
B
Usando la costruzione geometrica qui a fianco, è facile verificare che
sen θn = sen θ’n = xn / D
Le posizioni dei minimi di interferenza (nodi) sono
D
quindi date da:
d xn / D = (n + ½) λ
θ’n
R
Con ragionamento analogo si ricavano le posizioni dei
θn
S1
d
con n = 0, ±1, ±2, …
massimi di interferenza:
S2
d xm / D = m λ
con m = 0, ±1, ±2, …
Torniamo al caso della singola fenditura: applicando il principio di Huygens (fenditura = insieme di sorgenti
puntiformi) ed il principio di sovrapposizione, si
giunge ad una espressione per i minimi di diffrazione.
La strategia consiste nel considerare coppie di sorgenti
puntiformi a distanza fissata e applicare a queste un
ragionamento simile a quello appena visto per
l’interferenza prodotta da due sole sorgenti puntiformi.
Le
posizioni
dei
minimi
diffrazione sono:
axn
= nλ
D
con n = ± 1, ± 2, ± 3,...
di
Analogia con la luce:
Diffrazione della luce da singola fenditura:
Si può dimostrare che, quando la luce incidente
approssima un’onda piana monocromatica, la figura di
diffrazione osservata su uno schermo distante è
descritta, in ogni punto, dalla seguente
espressione dell’intensità luminosa I :
⎡
⎛ πa ⎞ ⎤
sen
⎜ θ ⎟⎥
⎢
⎝ λ ⎠⎥
I (θ ) = I ( 0 ) ⎢
⎥
⎢ πa θ
⎥
⎢
λ
⎦
⎣
2
dove I(0) è l’intensità al centro della figura di diffrazione (θ = 0°), λ è la lunghezza d’onda della luce, ed a
è la larghezza della fenditura. I minimi di intensità si troveranno ad angoli θ che
soddisfano la condizione:
π a θmin / λ = m π
(con m = ± 1, ± 2, ± 3 ...).
Nell’ipotesi di piccoli angoli, otteniamo la condizione per le posizioni (xmin)
dei minimi di intensità diventa:
ax min
= mλ (con m = ± 1, ± 2, ± 3,...).
D
Interferenza/diffrazione della luce da doppia fenditura:
Si può dimostrare che, quando un’onda piana monocromatica incide su una doppia fenditura, su uno
schermo lontano si osserva una
seguente
espressione
figura di interferenza/diffrazione descritta dalla
per
l’intensità
luminosa:
2
πa ⎞
⎛
⎜ sen( θ ) ⎟
λ ⎟ cos 2 ( πd θ )
I (θ ) = I (0)⎜
λ
⎜ πa
θ ⎟⎟
⎜
⎝ λ
⎠
I primi due termini dell’equazione sono identici alla
figura di diffrazione da singola fenditura (grafico
centrale, in cui si è posto a = 5 λ), ma questa ora è
moltiplicata
da
una
funzione
sinusoidale
dovuta
all’interferenza risultante dall’uso di due fenditure
(l’argomento del coseno dipende infatti dalla distanza tra
le fenditure d); nel caso d = 45 λ, la funzione sinusoidale
corrisponde alle frange di interferenza mostrate nel
grafico in alto.
Anche in questo caso, per angoli piccoli possiamo scrivere:
πd
πd x
θ≅
λ
λ D
la figura di interferenza ha un minimo di intensità
quando π d x / (λ D) = ± π/2, ± 3π/2, ± 5π/2, ... e un massimo di intensità
quando π d x / (λ D) = 0, ± π, ± 2π, ± 3π, .... Nell’approssimazione di piccoli
angoli, otteniamo le posizioni dei minimi di interferenza:
È facile verificare che
d xmin ⎛
1⎞
= ⎜ n + ⎟λ (con n = 0, ±1, ±2, ±3,...)
D
2⎠
⎝
e quelle dei massimi di interferenza:
d x max
= nλ
D
(con n = 0, ±1, ±2, ±3,...).
Applet diffrazione:
http://ww2.unime.it/dipart/i_fismed/wbt/ita/slitdiffr/slitdiffr_ita.htm ,
http://www.ba.infn.it/~fisi2005/evangelista/piccolo/tesi/Simulazione1.html;
quiz: http://www.ba.infn.it/~fisi2005/evangelista/piccolo/tesi/Quiz1p.html,
Applet interferenza:
http://www.ba.infn.it/~fisi2005/evangelista/piccolo/tesi/Simulazione2p.html,
quiz: http://www.ba.infn.it/~fisi2005/evangelista/piccolo/tesi/Quiz2p.html,
Applet interferenza e diffrazione:
http://www.ba.infn.it/~fisi2005/evangelista/piccolo/tesi/Simulazione3p.html
quiz: http://www.ba.infn.it/~fisi2005/evangelista/piccolo/tesi/Quizcasa3p.html,