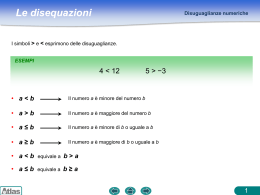
Le disequazioni
Appunti per la risoluzioni di
disequazioni algebriche intere e fratte
e per la risoluzione di
sistemi di disequazioni
Spesso gli studenti sono spaventati dalle difficoltà incontrate nella risoluzione
delle disequazioni, ma seguendo alcune semplici indicazioni, anche questo
argomento potrà essere affrontato con semplicità
Vediamo per prima cosa cos’è una disequazione:
Si tratta di una disuguaglianza tra due espressioni algebriche, per
esempio
f(x) > g(x)
Ma potrebbe essere anche f(x) < g(x), oppure
f(x) >= g(x), oppure f(x) <= g(x).
Già immagino qualche sguardo interrogativo….
Ma che sono f(x) o g(x)?
Niente paura! Sono delle espressioni “con la x”
(… certo, detto così qualche collega potrebbe inorridire, ma questi
appunti non li sto scrivendo perché vengano inseriti in un libro di
teoria, ma per avvicinarmi alle menti che oppongono più resistenza a
questo argomento!)
Per esempio è una disequazione:
2(x-3)-5 > (1-x)+x(3x-8)
Quando cerco la soluzione di una disequazione, troverò un intervallo di valori che
rende vera quella diseguaglianza
(sempre che esista!)
E che cos’è un intervallo?
Capire cos’è è semplice: guarda questo elenco di numeri
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Se ti dico “prendi l’intervallo tra 4 e 13”, quali valori scegli?
Forse mi potresti rispondere : “4 5 6 7 8 9 10 11 12 13”, ma potresti anche rispondere
“5 6 7 8 9 10 11 12”… qual è la differenza?
La differenza è negli estremi: nella prima risposta gli estremi sono compresi, nella seconda
no . La risposta è quindi condizionata dal modo in cui viene fatta la domanda, che dovrebbe
essere più precisa e specificare se si devono prendere oppure gli estremi.
Comunque, è importante conoscere bene il simbolismo:
[4,13] corrisponde a 4,5,6,7,8,9,10,11,12,13
[4,13[ corrisponde a 4,5,6,7,8,9,10,11,12
]4,13] corrisponde a 5,6,7,8,9,10,11,12,13
]4,13[corrisponde a 5,6,7,8,9,10,11,12
Per incominciare bisogna saper risolvere le disequazioni di primo grado,
cioè quelle in cui la x non ha mai un esponente.
2(x-5) –(2-x) < 3+6(1+x)
Sviluppo tutti i calcoli algebrici:
2x – 10 – 2 + x < 3 + 6 + 6x
Sposto i termini con la x a sinistra e quelli senza la x a destra
(ricorda di cambiare il segno ai termini che sposti e di mantenere lo stesso
segno a quelli che non si spostano)
2x +x – 6x < 3 + 6 + 10 – 2
Eseguo i calcoli a sinistra e poi quelli a destra
-3x < +17
Attenzione ora!
Il termine con la x è venuto negativo: c’è proprietà fondamentale delle
disequazioni che ci dice che in questo caso, prima di andare avanti con la
risoluzione devo cambiare il segno a tutti i termini della disequazione e il verso.
(se invece il termine con la x era positivo non dovevo fare questo cambiamento)
+ 3x > - 17
Ora divido a sinistra e a destra per il numero davanti alla x
+ 3x > - 17
+3
+3
Semplifico e moltiplico i segni a destra
x > - 17
3
Dunque la soluzione è : x > - 17/3 ….. che significa?
Significa che sono soluzione tutti i valori maggiori di -17/+3, cioè
i valori compresi tra -17/3 e +∞ (infinito).
Ma posso prendere come soluzione anche -17/3?
NO! Perché nella soluzione della mia disequazione c’è solo >.
Allora scriverò ]-17/3, +∞ [
Vediamo, quindi come scrivere al meglio la soluzione, ipotizzando tutti i casi che
si potrebbe presentare (la lettera b rappresenta un numero qualunque):
x>b
x >= b
x<b
x <= b
Tutti i valori maggiori di b, cioè da b fino a
+∞ , ma non posso prendere il valore b
Tutti i valori maggiori di b, cioè da b fino a
+∞ , posso prendere il valore b
Tutti i valori minori di b, cioè da - ∞ fino a b,
ma non posso prendere il valore b
Tutti i valori minori di b, cioè da -∞ a b,
posso prendere il valore b
]b, +∞[
[b, +∞[
]-∞, b[
]-∞, b]
Bene, ora siamo pronti ad imparare come risolvere le disequazioni di secondo grado,
cioè quelle in cui la x, alla fine dello svolgimento di tutti i calcoli, ha come massimo esponente il 2
2(x-5) –x(2-x) < -6 +6x(1+x)
Sviluppo tutti i calcoli algebrici:
2x – 10 – 2x + x2 < -6 + 6x + 6x2
Sposto tutti termini a sinistra:
(ricorda di cambiare il segno ai termini che sposti e di mantenere lo stesso segno a quelli che non
si spostano)
2x – 10 – 2x + x2 + 6 - 6x - 6x2 < 0
Eseguo i calcoli a sinistra e riordino i risultati in senso crescente
- 5x2 - 6x - 4< 0
Attenzione ora!
Poco ci importa se termine con la x al quadrato è venuto negativo:
Per risolvere una disequazione di grado superiore al primo noi impareremo un metodo
universale,detto studio del segno.
Studiare il segno significa individuare gli intervalli in cui il termine a sinistra della disuguaglianza è
positivo, negativo oppure nullo.
Tra questi intervalli saremo noi a scegliere quelli che sono soluzione della disequazione .
Risoluzione della disequazione
- 5x2 - 6x - 4< 0
Scompongo il termine a sinistra  in questo caso, avendo un trinomio di secondo grado,
1.
risolvo l’equazione associata trovando le due soluzioni x1 e x2 (se esistono)
2.
poi applico la relazione ax2+bx+c = a(x-x1)(x-x2)
x1,2= -(-6) +√(-6)2-4(-5)(-4)
2(-5)
= +6 + √36-20 = +6 + √16 = +6 + 4
-10
-10
-10
x1= -1
x2= -1/5
Quindi la scomposizione è: -5 (x + 1) (x +1/5)
Ora posso impostare nuovamente la mia disequazione, che diventa
-5 (x + 1) (x +1/5) < 0
Studio del segno:
1. -5 sempre negativo (non ha la x, guardo solo il segno che ha davanti)
2. x + 1 >< 0  x >< -1
3. x + 1/5 >< 0  x >< -1/5
Osservazione:
nell’impostare i segni metto sempre prima il maggiore  tale impostazione non
dipende dal segno del testo
A questo punto devo costruire una tabella che rappresenta i segni che possono
assumere i singoli fattori:
Disegno un asse orientato e fisso su di esso i valori trovati:
-1
- 1/5
La tabella deve avere tanti livelli quanti sono i fattori della scomposizione:
nel mio caso sono tre
-1
- 1/5
1.
2.
3.
Ragioniamo:
Al livello uno devo rappresentare la condizione “sempre negativo”, per cui disegnerò
una linea tratteggiata dall’inizio alla fine (il tratteggio significa “meno”)
Al livello due, guardo il verso della prima freccia … se ne va verso destra, per cui disegno una linea continua verso destra a partire da -1. Completo il livello mettendo il tratteggio nello spazio rimasto vuoto.
Al livello tre , guardo il verso della prima freccia … se ne va verso destra, per cui
disegno una linea continua verso destra a partire da -1/5. Completo il livello mettendo
il tratteggio nello spazio rimasto vuoto.
Dunque l’aspetto finale della mia tabella è il seguente:
-1
-1/5
1.
2.
3.
Ricorda che il tratteggio rappresenta il segno meno, la linea continua il segno +;
Devo ora calcolare il segno in ogni colonna, moltiplicando (regola pratica: conta
quanti sono i tratteggi, se sono dispari viene meno, se sono pari viene più)
Quindi, in ogni colonna, il segno corrispondente è:
-1/5
-1
1.
2.
3.
_
+
_
A questo punto devo scegliere l’intervallo o gli intervalli (se sono più di uno) :
Guardo il testo e controllo qual è il verso della disequazione: - 5x2 - 6x - 4< 0
Poiché è < devo scegliere gli intervalli con il meno (se fosse stato > avrei scelto gli
intervalli con il più).
Quindi, dovendo scegliere gli intervalli con il meno, prederò quelli colorati:
-1/5
-1
-∞
+∞
1.
2.
3.
_
+
_
Scrivo la soluzione:
Osserva che in questa tabella non ci sono “pallini” che si mettono soli se nel testo
c’è l’uguale: allora devo prendere dal -∞ a -1 e poi da -1/5 a +∞, escludendo gli
estremi (niente pallini!)  ] -∞ , -1[ e ]-1/5, +∞[ .
I due intervalli collegano con un simbolo che significa “unione”: ] -∞ , -1[ U ]-1/5, +∞[
Bene, abbiamo imparato a risolvere una disequazione di secondo grado, ma
devi fare tanti esercizi per diventare sicuro del procedimento.
Aggiungo solo una piccola cosa: prima ho parlato di “pallini”…entrano in gioco
quando nel testo c’è l’uguale.
Se avessi dovuto risolvere
-5x2 - 6x - 4<= 0
il procedimento non sarebbe cambiato molto:
- Stessa scomposizione
- Nell’impostazione dello studio del segno sarebbe comparso anche il segno di
uguale
Studio del segno:
1. -5 sempre negativo (non ha la x, guardo solo il segno che ha davanti)
2. x + 1 >=< 0  x >=< -1
3. x + 1/5 >=< 0  x >=< -1/5
- Tabella dello studio del segno uguale, ma integrata da “pallini” quando c’è l’uguale
-1
-1/5
1.
2.
o
3.
o
_
+
_
Scriviamo ora gli intervalli soluzione, facendo attenzione ad includere anche il
-1 e il -1/5 (basterà usare le parentesi chiuse vicino a questi due valori).
Ne approfitto per ricordarti che in corrispondenza dell’infinito le parentesi sono
sempre aperte:
] -∞ , -1] U [-1/5, +∞[
E se ne testo ci fosse stato il maggiore al posto del minore?
Semplice, avrei scelto l’intervallo con il più, tutto il resto sarebbe stato identico
E se avessi una disequazione di grado superiore al secondo?
Procedimento identico:
1. Scomposizione (qui ci vogliono un minimo di abilità algebriche, si usano raccogliere eventuali fattori comuni, riconoscere prodotti notevoli, scomporre trinomi di
2° grado, ecc)
2. Fare lo studio del segno, costruendo una tabella che ha tanti livelli quanti sono
i fattori che ti sono venuti dalla scomposizione
3. Scegliere gli intervalli soluzione guardando il verso nel testo
E se avessi una disequazione fratta?
Procedimento identico:
1. Scomposizione di numeratore e denominatore (solite di abilità algebriche!)
2. Fare lo studio del segno. Attenzione! Se nel testo c’è l’uguale, questo si mette
solo nei fattori del numeratore, nel denominatore NO
2. La tabella che ha tanti livelli quanti sono i fattori che ti sono venuti dalla
scomposizione di numeratore e denominatore
3. Scegliere gli intervalli soluzione guardando il verso nel testo, facendo attenzione
a come scrivi gli intervalli soluzione (a volte il pallino c’è solo da una parte!)
Allora, ti sono schiarite un po’
le idee???
Manca ancora una cosa: mi spiace dobbiamo continuare!!!!
Dobbiamo imparare a risolvere un sistema di disequazioni.
Cosa significa cercare la soluzione di un sistema di disequazioni?
significa individuare,se esistono, gli intervalli comuni di soluzioni tra più disequazioni.
È un po’ come quando più persone partono da casa loro per andare al lavoro:
Supponiamo che Aldo, Giovanni e Giacomo ogni mattina vadano al lavoro a piedi.
Di solito si incontrano tutti e tre nell’ultimo tratto di strada: la parte di strada che percorrono chiacchierando insieme rappresenta la soluzione del sistema composto
dai tre tragitti casa-lavoro.
Aldo
Soluzione del
Sistema
“tragitto”
Se non si incontrassero contemporaneamente
tutti e tre,tale sistema non avrebbe soluzione!
Giovanni
Giacomo
Supponiamo di dover risolvere questo sistema:
A) 5 –x <= 0
B) (x-2)(x+3) > 0
C) (x-4) / (- x - 2) >= 0
Risolvo separatamente le disequazioni messe a sistema, utilizzando tutte le tecniche
imparate precedentemente:
A) È di 1° grado, non serve fare lo studio del segno:
-x >= -5  x <= 5  ]-∞, 5]
B) È già scomposta, faccio lo studio del segno e scelgo le zone con il più (c’è >nel testo)
1) x-2 ><0  x><+2
2) x+3><0  x><-3
-3
+2
1)
2)
+
_
+
La soluzione è (attento, nessun pallino!) : ] -∞ , -3[ U ]+2, +∞[
C) È un disequazione fratta, già scomposta. Posso fare subito lo studio del segno:
N) x-4 >=< 0  x>=< +4
D) - x - 2 > < =  - x > < +2  x< >-2
Hai notato che l’uguale è solo al numeratore?
Hai notato che al denominatore - a causa del meno davanti alla x - ho cambiato
segno e versi?
Costruisco la tabella (attento! Al denominatore il primo segno da verso sinistra)
e scelgo la zona con il più (nel testo c’è >=)
-2
+4
D)
N)
_
o
+
_
La soluzione è (occhio al pallino!): ]-2, +4]
A questo punto costruisco una nuova tabella che deve rappresentare SOLO
le soluzioni del sistema. Osserviamo che
• la tabella delle soluzioni deve avere tanti livelli quante sono le disequazioni
messe a sistema
• in questa tabella non ci sono linee tratteggiate!
infatti si rappresentano le soluzioni con delle linee continue
• la soluzione è rappresentata dagli intervalli che sono CONTEMPORANEAMENTE
soluzione su tutti i livelli
Mi riscrivo per bene le singole soluzioni in corrispondenza delle disequazioni del testo:
A)
]-∞, +5]
B)
] -∞ , -3[ U ]+2, +∞[
C)
]-2, +4]
Tabella delle soluzioni del sistema:
-∞
-3
-2
+2
+4
+5
+∞
o
A)
B)
C)
o
La soluzione è quella evidenziata : ]+2, +4] , poiché è l’unica colonna in cui i tre
livelli hanno contemporaneamente la linea continua.
A questo punto io ho finito,
ora toccherà a te fare esercizio!!!
Esercizi
Predila con filosofia, sono solo un po’ di
esercizi!!!,
un regalino di buon inizio d’anno!!!
x2 -1 > 0
(2-x) / (x+4) <=0
x2 (x2 +10x + 25)(x2 + 6x + 9) >=0
x+2>+3
2x-1>x+5
x2-x-2>= 0
16 – x2 > 0
Altri esempi e le soluzioni a questo indirizzo:
http://share.dschola.it/helpmat/marconi/4ltb/Materiali/esercizi%20svolti%20disequazioni%20qualsiasi%201.pdf
Ringrazio il prof G.Girgenti dell’IIS Marconi Galletti Domodossola (VB) per aver reso disponibile in rete questo
utile materiale!
Prof.ssa Anna Maria Pizzolla – ITC Piero Calamandrei - Roma