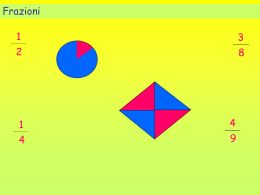
I numeri rotti:
Un nuovo mondo numerico nella
scuola primaria!
Relatore: Prof.ssa Ana Millán Gasca
Correlatore: Dott.ssa Viviana Rossanese
Laureanda: Ilaria Papi
Quadro teorico
ANA MILLÁN GASCA
Appunti delle lezioni di Matematica e didattica della matematica, Roma,
Università degli studi Roma Tre, Roma 2009
MARIA TERESA MARRANO, EMANUELA SPAGNOLETTI ZEULI
Alcuni punti critici dell’insegnamento della matematica nella scuola
primaria
Laboratorio di Matematica e didattica della matematica, Università degli
studi Roma Tre, Roma 2010.
Alcuni testi di riferimento:
Idea base del Progetto
La frazione è, insieme, un nuovo tipo di numero e una
notazione simbolica di radici molto antiche. Come notazione
pura ha molte interpretazioni e si collega all’idea di parte
dell’unita, di operatore, di percentuale, di rapporto. Come
numero rinvia all’estensione del campo numerico da N a Q, e
quindi a varie forme di scrittura (decimale, sessagesimale), alle
rappresentazioni sulla retta e, in quanto nuovo tipo di numero,
le frazioni si possono confrontare e operare.
Le ricerche più recenti in didattica della matematica
suggeriscono che il lavoro con i bambini deve esplorare questa
rete di idee stabilendo dei nessi logici grazie al lavoro con molti
esempi concreti (geometria, grandezze, misure,capacita,
monete, tempo, musica,ecc).
…da N a Q!
Q
Z
N
Addizione
Moltiplicazione
Sottrazione
Divisione
La
frazione…
“ieri sera ho
mangiato mezza
pizza perché
l’altra metà l’ha
mangiata mio
fratello!”
“Borgo Hermada è una frazione di
Terracina”
“La settimana prossima andiamo in gita e per
farlo dobbiamo essere la metà della classe!”
“…manca un quarto
d’ora alla fine della
lezione!”
“La mia
maglia ha le
maniche a
tre quarti!”
La frazione unitaria
“Ho diviso il tutto in n pezzi e ne ho preso uno!”
La frazione unitaria...fare due, tre, quattro,...
parti!
In generale, la frazione
esprime un rapporto:
il doppio (la metà), il triplo
(un terzo), il quadruplo (un
quarto), … e poi due terzi,
tre quarti, ...
Dalla frazione al “tutto”!
La frazione complementare:
Una gara di corsa!
Bruno sta partecipando ad una gara di corsa
…dove si trova Bruno a 30 secondi dal via?
Bruno ha percorso l’1/3 del tragitto … quindi per raggiungere
l’arrivo deve ancora percorrerne i 2/3!
1/3 e 2/3 sono frazioni complementari, perché 1/3+2/3 = 3/3 = 1!
1/3
1/4
1/2
1/4
1/6
“Ma sei noi volessimo più parti
rispetto a quelle che ha
l’intero???”
“Una sera ero in una pizzeria e ho ordinato una bella
pizza margherita. L’ho divisa in 5 spicchi uguali e l’ho
mangiata tutta, ma siccome avevo molta fame avrei
voluto altri due spicchi per saziarmi e quindi cosa ho
fatto?”
“Hai ordinato un’altra pizza?!”
“Giusto!...quindi ho mangiato i 7/5 della pizza!”
Frazioni sorelle
“Oggi la maestra ci ha spiegato le frazioni sorelle. Veramente si
chiamano frazioni equivalenti,
però questo nome è più brutto.
Sono frazioni che sembrano diverse e invece, se ci rifletti, capisci che
sono la stessa cosa perché valgono la stessa quantità. Noi già lo
sapevano da quando abbiamo studiato la frazione ½ e la frazione 2/4.
Sempre mezza mela è!
Allora tutti ci siamo messi a inventare frazioni sorelle di ½. Io ho
inventato 4/8 e 3/6 e ho scoperto una cosa bella, che anche Bianca
aveva inventato le stesse frazioni!”
(Cerasoli Anna, 2010)
Di una buona torta
preferiresti avere i
4/5 o i 5/6?
(Rispondi e motiva la tua risposta)
Frazione come operatore!
Alla fiera di Terracina, su una bancarella c’erano 15
leccalecca di uguale misura e Sofia ne ha comprato 1/5.
Quanti leccalecca ha comprato?
o
15 : 5 = 3
3x1=3
Frazione come rappresentante di
un numero decimale
1/2 = uno diviso due = 0,5
1/2
0,5
“…man mano che vai avanti i numeri diventano sempre più
grandi, invece le frazioni diventano sempre più piccole”
Io conto
Offerta della compagnia telefonica:
“Per ogni 10 euro di ricarica,
noi aggiungiamo 5 euro
così risparmia la metà!”
???
Le percentuali sono frazioni!
“Non l’avevo mica capito che 10% significa proprio 10/100.
Ecco perché in quel simboletto fatto così % ci sono la linea
di frazione e i due zeri del 100”
Situazione problematica:
Attenzione ai saldi!
“Questo fatto è successo alla nostra maestra […] è andata in un negozio per
comprare una cosa che costava 200 euro. Siccome c’erano i saldi, le avevano detto
che scontavano il 30 %, perciò lei stava tranquilla e già pensava che le toglievano 60
euro. Invece quando è andata a pagare, la cassiera le ha detto che lo sconto era del
20% più il 10%. E lei si è arrabbiata!...perché?
Anche per la musica servono le frazioni!
La somma tra diciotto e sei
La differenza tra nove e sette
Il rapporto tra cinque e quindici
La somma tra il precedente di quattro e il successivo di nove
La metà della differenza tra sedici e dieci
Il triplo della somma tra 2 e 4
La metà della metà di venti
Tre quarti di dodici
Il dieci per cento di ottantacinque
Il sessanta per cento di trentaquattro
La somma tra i triplo di sei e il doppio di sette
Analisi dei sussidiari
La matematica e lo scoutismo
GIOCHI SCOUTS
Limoni
Ruba bandiera
La serie dei numeri
Attenzione al
minuto
Attraverso il gioco il bambino impara a conoscere se stesso ed
“ha bisogno della dimensione del gioco per stare bene”!
Punti deboli del progetto
Terminologia
Intero (tutto)
Unità frazionaria
(frazione unitaria)
Presentazione della collocazione della frazione sulla linea dei
numeri;
Frazione come
numero
Concetto di
infinito
Rapporto tra numeri e
geometria
“La matematica non è una foresta buia
ma una sequenza di finestre che si
aprono nella vita di ogni giorno”
Cerasoli Anna,2010