ELEMENTI DI CINETICA CHIMICA
III.1 Velocità di reazione
I cambiamenti chimici (reazioni chimiche) sono governati dalla termodinamica, che coinvolge gli
aspetti energetici del processo, dai quali dipende, ad esempio, la spontaneità del processo stesso,
ma anche dalla cinetica, che riguarda il tempo necessario perché un processo avvenga. La
cinetica chimica studia la “velocità” dei processi chimici, cioè la variazione nel tempo della
quantità e qualità delle specie chimiche che vi partecipano e le relazioni che la legano alla
composizione del sistema (concentrazione delle diverse specie presenti), alla temperatura e alla
pressione e agli altri fattori chimico-fisici. La finalità di tali tipi di studi è sostanzialmente duplice:
da una parte la conoscenza e/o previsione dei tempi di reazione, cioè del tempo necessario per
ottenere una determinata conversione da reagenti a prodotti; dall’altra la conoscenza del
meccanismo della reazione, cioè dell’insieme dei passaggi (steps) e delle specie chimiche
intermedie che costituiscono la reazione in questione (per cui, la conoscenza del meccanismo
richiederebbe sempre la conoscenza e la caratterizzazione degli intermedi attraverso studi non
cinetici). Per la comprensione del meccanismo è assolutamente indispensabile un’adeguata
conoscenza della cinetica (anche se le conoscenze cinetiche possono sconfessare un meccanismo,
ma non possono mai stabilirlo da sole).
La gamma di reazioni chimiche e delle caratteristiche cinetiche è estremamente ampia, basti
pensare al caso apparentemente più banale di una miscela H2/O2 che dà H2O. La termodinamica è
in grado di dirci che tale reazione ha un ∆G o = –228.57 kJmol–1 e ∆H o = –241.82 kJmol–1, dal che
deduciamo che si tratta di una reazione “fortemente spontanea”, perché notevolmente esotermica.
Eppure il tempo di semivita, cioè quello necessario per avere il dimezzamento di un reagente, può
variare da 10-6 s a 1025 anni, a seconda che si inneschi la reazione con una scarica o una fiamma
ottenendo una esplosione, oppure si lasci la miscela isolata. D’altra parte le reazioni chimiche
avvengono in condizioni di stato fisico estremamente diverse, in fase omogenea o eterogenea,
ecc., per cui si ha una molteplicità di situazioni.
Una reazione chimica è quindi caratterizzata completamente quando se ne conosca la
stechiometria, l’energetica e la cinetica. Chiaramente stechiometria ed energetica sono
strettamente correlate, dato che la prima definisce lo stato iniziale e lo stato finale del processo ai
quali è riferito qualsiasi bilancio energetico si voglia fare.
Ricordiamo che, data una reazione chimica
aA + bB + •••• = •••• + xX + yY + zZ
∑νiSi = 0
dove la seconda espressione rappresenta una forma compatta di esprimere la stechiometria
esplicitata nella prima espressione. Ricordiamo che i νi sono i coefficienti stechiometrici, con la
convenzione che si intendono positivi quelli dei prodotti e negativi quelli dei reagenti.
Si possono avere situazioni in cui la stechiometria rimane la stessa durante tutto il processo, per
cui si parla di stechiometria indipendente dal tempo, ma si possono avere casi in cui la
stechiometria dipende dal tempo, quando la reazione procede attraverso la produzione di
intermedi che possono accumularsi durante il decorso della reazione; ad esempio la
decomposizione termica dell’acetone
2CH3COCH3 = 2CH4 + C2H4 + 2CO
passa attraverso la formazione di chetene che si accumula nel tempo:
2CH3COCH3 = CH4 + CH2CO
2CH2CO = C2H4 + 2CO
41
per cui non si è in grado di dire con esattezza quale sia la stechiometria se non si tiene conto
anche della cinetica delle varie reazioni coinvolte.
Data una reazione chimica con stechiometria indipendente dal tempo (cioè non si ha accumulo di
intermedi in quantità sensibile), si definisce il grado di avanzamento della stessa ξ (concetto
introdotto nel 1922 da T. de Donder):
ξ=
n i − n 0i ∆n i
=
νi
νi
cioè il rapporto tra il numero di moli di prodotto i-esimo formatesi, o il numero di moli del reagente
i-esimo scomparse, al tempo t ed il suo coefficiente stechiometrico. E’ subito chiaro che, entrando
in gioco i coefficienti stechiometrici νi (i νi dei prodotti sono positivi, mentre quelli dei reagenti
sono negativi, per cui ξ è sempre una quantità positiva), il valore del grado di avanzamento di una
reazione dipende da come si esprime la stechiometria. In cinetica la stechiometria deve essere
sempre espressa con numeri interi.
La termodinamica ci dimostra che il decorso della reazione chimica a stechiometria indipendente
dal tempo, 0 = ∑νiSi, comporta una diminuzione di energia libera di Gibbs, che, a T e p costanti, è:
per cui si ha:
e, all’equilibrio:
dG =  –SdT + Vdp + ∑µidni = (∑νiµi)dξ
∆rG = (∂G/∂ξ)T,p = ∑νiµi = ∆G o + RTln Q = ∆G o + RTln∏aiνi
(∂G/∂ξ)T,p = 0 = ∆rG = ∆rG o + RT ln K
RT ln K = RT ln (∏aiνi)eq = –∆rG o
ottenendo che se (∂G/∂ξ)T,p < 0, la reazione procede spontaneamente, a T e p costanti, da sx a
dx; viceversa se (∂G/∂ξ)T,p > 0, la reazione procede spontaneamente da dx a sx, mentre è
all’equilibrio, e quindi non produce più alcun cambiamento nel tempo, se (∂G/∂ξ)T,p = 0.
Dai dati termodinamici possiamo ricavare sostanzialmente solo le suddette informazioni e cioè
sapere se una reazione chimica, o meglio se una data miscela di sostanze chimiche, è all’equilibrio
o no e, in questo caso, verso quale condizione di equilibrio è in grado di muoversi. Nulla ci può
essere detto circa il tempo necessario per raggiungere la condizione di equilibrio.
E’ opportuno ricordare la relazione termodinamica fondamentale che lega le grandezze in gioco in
un processo a temperatura costante:
∆rG = ∆rH – T∆rS
Un concetto fondamentale in cinetica è quello di velocità di reazione. La velocità di reazione
esprime in qualche modo la velocità con cui una reazione chimica decorre, cioè la velocità con cui
le specie chimiche si trasformano; si può pensare allora di esprimere la velocità di reazione
attraverso la velocità di formazione o di consumo di una specie chimica coinvolta:
vi = (dni/dt) se i è un prodotto (velocità di formazione)
vj = –(dni/dt) se i è un reagente (velocità di scomparsa)
o, meglio, per renderla indipendente dal volume complessivo V del sistema considerato,
vi = (1/V)(dni/dt) = (dci/dt)
vj = (1/V)(dni/dt) = (dci/dt)
se i è un prodotto (velocità di formazione)
se i è un reagente (velocità di scomparsa)
peraltro è chiaro che le diverse vi, pur essendo correlate tra di loro attraverso la stechiometria
della reazione, sono diverse da specie a specie. Volendo definire la velocità di reazione in modo
42
univoco per una data reazione, conviene allora utilizzare la seguente espressione per la velocità
(per unità di volume):
v≡
1 d ξ 1 dci
≡
V dt ν i dt
[v] = mol•L-1s-1; mol•dm-3 s-1;
mol•m-3 s-1; kmol•m-3 s-1
che dipende dalla stechiometria della reazione (cioè dai νi), ma non dipende dalla particolare
specie chimica alla quale ci si riferisce.
Consideriamo ad esempio la seguente reazione
2H2 + O2 → 2H2O
v ≡
1 d [H 2 ]
1 d [H 2 ]
≡−
− 2 dt
2 dt
v ≡
1 d [O 2 ]
d [O 2 ]
≡−
− 1 dt
dt
v ≡
1 d [H 2 O ] 1 d [H 2 O ]
≡
+2
dt
2
dt
Non si deve ignorare la possibilità che durante il decorso della reazione il volume del sistema possa
cambiare durante il decorso della reazione. È chiaro che in questa situazione si avrebbe una
variazione della concentrazione delle specie dovuta esclusivamente alla variazione di volume, al di
là del contributo cinetico, per cui non si può più esprimere la velocità della reazione come la
variazione della concentrazione tout court.
v = 1 dci + ci dV
ν i dt ν i V dt
dni = Vdci + cidV
e analoghe considerazioni vanno fatte per le velocità di formazione e di consumo.
E’ chiaro che studiare la velocità di una reazione significa stabilire da quali parametri e in che
modo essa dipenda: concentrazione (reagenti, prodotti, intermedi), parametri operazionali (T e p),
proprietà dell’eventuale solvente (η ed ε), forza ionica e pH, presenza di catalizzatori/inibitori,
effetto di superficie (rapporto S/V), effetti isotopici.
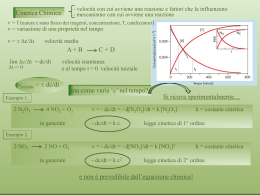
III.2 Legge cinetica
La velocità di reazione è, ovviamente, funzione della concentrazione delle specie chimiche
coinvolte nella stessa. La funzione matematica che esprime questa dipendenza viene definita
legge cinetica della reazione e, in generale, non può essere dedotta direttamente dalla
stechiometria della stessa, per cui deve sempre essere determinata sperimentalmente.
Per semplicità ci limiteremo intanto a considerare un sistema chiuso, isotermo e omogeneo, il che
rappresenta una sensibile semplificazione, ma un caso largamente diffuso per cui vale senz’altro la
pena di essere affrontato. Ciò significa che non verranno considerati sistemi aperti (processi a
flusso, fiamme), né -per il momento- sistemi eterogenei (reazioni di superficie).
Nella tabella seguente sono riportati alcuni esempi di reazioni chimiche, con le relative
stechiometrie e leggi cinetiche. Il primo aspetto che deve essere evidenziato è che la legge
cinetica non può essere desunta dalla stechiometria, per lo meno non in modo diretto: la legge
cinetica può essere ricavata solo sperimentalmente, cioè mediante lo studio cinetico della reazione
in esame.
43
LEGGE CINETICA
STECHIOMETRIA
CH2
= CH3−CH=CH2
H2 C
v = − (d[CP]/dt) = k[CP]
CH2
v = − (d[H2]/dt) = k1[H2][I2] − k−1[HI]2
[HI] = 0 (fase iniziale o rimuovendolo)
v0 = − (d[H2]/dt) = k1[H2][I2]
partendo da HI, rimuovendo i prodotti
v0 = − (1/2)(d[HI]/dt) = k-1[HI]2
H2 + I2 = 2HI
H2 + Br2 = 2HBr
v = (1/2)(d[HBr]/dt) =
= {k[H2][Br2]1/2}/{1 + k’[HBr]/[Br2]}
v0 = k[H2][Br2]1/2
2NO + Cl2 = 2NOCl
v = (1/2)(d[NOCl]/dt) = k[NO]2[Cl2]
OCl− + I− = OI− + Cl−
v = (d[Cl−]/dt) = {k[OCl−][I−]/[OH−]}
CH3CHO = CH4 + CO
v = (d[CH4]/dt) = k[CH3CHO]3/2
In molti casi la legge cinetica è un’equazione del tipo:
v = f(c) = k[A]α [B]β •••
dove k, α, β, ... sono indipendenti dalla concentrazione e dal tempo. In questo caso, cioè se la
legge cinetica è del tipo su riportato, una produttoria di concentrazioni con esponente anche
frazionario, si dice che la reazione ammette un ordine (concetto introdotto da Ostwald nel 18879,
che non deve essere confuso con la molecolarità. La molecolarità è infatti un dato
stechiometrico, cioè il numero di molecole di reagenti presenti nella stechiometria. L’ordine di
reazione, invece, è un dato cinetico, che può esserci, se la legge cinetica è un’equazione
matematica del tipo su descritto, altrimenti la reazione non ammette ordine.
L’esponente α è definito come ordine di reazione rispetto alla specie A, mentre n = α + β + ••• è
definito come ordine (complessivo) della reazione.
La reazione di conversione del ciclopropano (CP) in propilene è una reazione del primo ordine,
mentre la reazione di formazione di HI, nella fase iniziale o in presenza della rimozione del
prodotto, è una reazione del secondo ordine, primo ordine rispetto ad H2 e primo ordine rispetto a
I2, così come è del secondo ordine la reazione di decomposizione di HI se si rimuovono i prodotti
della stessa; la reazione di decomposizione dell’acetaldeide è di ordine 3/2.
Si è visto però, dagli esempi su riportati, che non tutte le reazioni ammettono ordine, anche
quando la stechiometria è abbastanza semplice, il che porta a precisare alcune osservazioni:
• l’ordine di una reazione è un dato squisitamente sperimentale, che non può essere dedotto
automaticamente dalla stechiometria della reazione;
• l’ordine di una reazione è un numero razionale, può essere frazionario, nullo, negativo;
• un ordine frazionario indica sempre una reazione composita (complessa), mentre un ordine
intero non è sempre indice di reazione semplice;
• in generale l’ordine è diverso dalla molecolarità.
Una reazione viene definita elementare quando avviene in un unico step, cioè quando le specie
reagenti si incontrano in un unico passaggio per trasformarsi in prodotti; in tal caso non si ha
formazione di specie intermedie. Per una reazione elementare l’ordine corrisponde alla molecolarità
44
poiché il numero di molecole che si devono incontrare per dare luogo alla reazione è esattamente
quello previsto dalla stechiometria (dato che la reazione avviene in un unico step). Così si hanno
reazioni elementari unimolecolari, bimolecolari, trimolecolari, anche se reazioni elementari
trimolecolari sono piuttosto rare, dato che la probabilità di avere l’incontro simultaneo di tre
molecole, in posizione spaziale conveniente, è piuttosto bassa. Chiaramente per poter definire la
molecolarità di una reazione elementare (oggetto di interesse della dinamica molecolare) bisogna
aver verificato tutte le conoscenze in merito e aver scartato qualsiasi possibilità di esistenza di
stadi diversi (e quindi di intermedi), mentre l’ordine descrive molto semplicemente la dipendenza
della velocità dalla concentrazione.
Peraltro la definizione di una reazione elementare può essere inficiata da carenze di conoscenze o
da situazioni particolari. Ad esempio la reazione di formazione di HI è stata lungamente
considerata una reazione elementare, mentre si è scoperto che anch’essa avviene, almeno in
parte, con un meccanismo a stadi (anzi più meccanismi a stadi, a seconda di T), anche se con
limitato contributo. D’altra parte è possibile che un reagente presente in largo eccesso (solvente)
subisca limitate variazioni di concentrazione da non essere rilevate e quindi non figuri
esplicitamente nella legge cinetica facendo pensare di non essere coinvolto; così come si hanno
sostanze (catalizzatori) che, pur partecipando alla reazione, figurano sia tra i reagenti che tra i
prodotti, per cui la loro concentrazione non varia nel corso della reazione e, quindi, non figura
formalmente nella legge cinetica, anche se v dipende dal valore di cCAT.
Le reazioni che non sono elementari, cioè che coinvolgono più stadi, vengono definite reazioni
composite. Per una reazione composita la molecolarità non è rilevante ai fini cinetici, così come è
possibile che non ammettano ordine. Gli stadi elementari che costituiscono una reazione composita
sono sostanzialmente di tre tipi: reazioni simultanee (dette anche parallele), opposte (reazioni
reversibili), consecutive (in successione, possibilità di feed-back). Un caso particolare è costituito
dalle reazioni a catena, quando un reagente consumato in uno step viene riformato in un altro ed
il ciclo consumo-formazione si ripete parecchie volte.
Si capisce abbastanza facilmente che il caso di reazioni simultanee, così come quello di reazioni
reversibili, non ammette ordine, in quanto la legge cinetica conterrà termini additivi. Ora poiché
tutte le reazioni chimiche sono termodinamicamente reversibili, ∆G 0 è sempre finito, per cui non
dovrebbero mai ammettere ordine. Però si hanno molte reazioni per le quali il grado di
avanzamento ξ all’equilibrio è tale che le quantità di reagenti ancora presenti siano irrilevabili, per
cui si può parlare di reazione praticamente irreversibile, della quale si può definire l’ordine e
misurarlo sperimentalmente. Naturalmente, il fatto che una reazione non ammetta ordine non
deve essere confuso con il fatto che essa non abbia una legge cinetica ben definita.
Abbiamo visto che nella legge cinetica di una reazione che ammette ordine, figura una costante di
proporzionalità k, detta costante cinetica, le dimensioni della quale dipendono dall’ordine della
reazione, dato che v si misura sempre allo stesso modo (per le reazioni in fase omogenea, v si
misura in mol dm-3s-1), per cui la costante cinetica di una reazione di primo ordine si misura in s-1,
quella di una reazione di secondo ordine in dm3mol-1s-1, ecc..
III.3 Determinazione della legge cinetica
Determinare la legge cinetica di una reazione significa determinare l’equazione che lega la velocità
di reazione a tutte le specie chimiche coinvolte, cioè reagenti e prodotti e ad eventuali sostanze
aggiunte, il che significa determinare i relativi ordini e la o le costanti cinetiche. Oltre a ciò è
importante conoscere anche l’effetto della temperatura, del quale si dirà più avanti.
Si capisce in maniera intuitiva che è necessario determinare gli andamenti nel tempo delle
concentrazioni delle varie specie e, da questi, ricavare l’espressione matematica v ≡ (dc/dt) = f(c).
Naturalmente sarà necessario utilizzare le tecniche analitiche più svariate per poter seguire nel
tempo la concentrazione delle diverse specie chimiche, anche se non è necessario conoscere gli
andamenti di tutte quelle coinvolte (in particolare degli intermedi e, qualche volta, dei prodotti).
Disponendo di dati c = f(t), in forma numerica o grafica (monitoraggio discontinuo o continuo), si
possono utilizzare sostanzialmente due metodologie di analisi di tali dati: il metodo differenziale,
45
che consiste nel ricavare il valore di v dai dati sperimentali, misurando direttamente (dc/dt), cioè
la pendenza della curva c=f(t), senza che sia necessaria alcuna ipotesi a priori sulla legge cinetica
e quindi sul meccanismo; il metodo di integrazione, che presuppone invece un’ipotesi sulla legge
cinetica (quindi sul meccanismo) e da tale legge cinetica si calcola per integrazione la funzione
c=f(t) con la quale si confrontano poi i dati sperimentali e in base al migliore fitting con le diverse
curve teoriche, corrispondenti a diverse leggi cinetiche, si determina qual è quella più adeguata e,
quindi, i valori dei parametri cinetici. In generale si preferisce seguire l’andamento della
concentrazione dei reagenti, soprattutto quando si abbiano meccanismi semplici, salvo che non sia
più semplice dal punto di vista analitico seguire quella dei prodotti (ad esempio idrolisi di un
alogenuro, conversione di uno zucchero).
Il metodo di integrazione, suggerito già da Wilhelmy nel 1850, richiede di partire da una ipotesi
per la legge cinetica dalla cui integrazione si ricava la curva teorica c=f(t) da confrontare con i dati
sperimentali, rappresentati nel modo più adeguato (possibilmente lineare). Come vedremo, la
funzione c=f(t) dipende dall’ordine di reazione o, più propriamente, dalla legge cinetica. I casi più
frequenti sono quelli in cui n = 0, 1 0 2. E’ chiaro, peraltro, che n = 0 non può rappresentare una
reazione elementare, mentre n = 1 e n = 2 potrebbero essere riferiti a reazioni elementari, anche
se non basta il valore dell’ordine per stabilire se la reazione è elementare o composita.
Le reazioni di ordine zero hanno una stechiometria con molecolarità bassa, spesso uni
molecolare
A → P

ed una legge cinetica in cui la concentrazione del reagente è elevata a 0, per cui non figura nella
legge cinetica (c 0 = 1)
v ≡ –(d[A]/dt) = k[A]0 = k
Si tratta di una legge cinetica che riguarda reazioni di superficie, come ad esempio la
decomposizione di NH3 su W; oppure alcune reazioni enzimatiche. In questo caso, poiché la
velocità v si misura in mol dm-3s-1, anche k si misura in mol dm-3s-1. L’aspetto singolare di queste
reazioni è che la velocità è costante e indipendente dalla concentrazione del reagente, che invece
diminuisce nel tempo, dato che scompare a causa della reazione.
Per integrazione della legge cinetica (che è un’equazione differenziale) si ottiene c=f(t)
d [A] = − kdt
[A]
[A]0
t
∫[A] d[A] = −k ∫0 dt
[A]
0
[A] = [A]0 − kt
-k
andamento lineare di [A] con t, con pendenza –k ed intercetta
[A]0, cioè il valore iniziale della concentrazione del reagente.
0
Un parametro importante per caratterizzare una reazione
t
chimica è il tempo di dimezzamento o il tempo di semivita. In realtà si tratta di due grandezze leggermente diverse, anche se molto spesso sono la
stessa cosa. Il tempo di dimezzamento è il tempo necessario perché la concentrazione del
reagente diventi metà del suo valore iniziale, cioè si sia trasformata metà del reagente disponibile,
cioè si abbia [A] = [A]0/2. Il tempo di semi-vita è il tempo necessario perché si trasformi metà del
reagente trasformabile, che è la differenza tra la concentrazione iniziale [A]0 e la concentrazione
finale [A]∞, cioè si abbia [A] = ([A]0 + [A]∞)/2. Ovviamente, se a fine reazione tutto il reagente è
scomparso, i due tempi sono esattamente la stessa cosa, poiché [A]∞ = 0. Viceversa, quando a
fine reazione [A]∞ ≠ 0 (reazioni reversibili) i due tempi sono diversi, in particolare il tempo di semivita risulta minore del tempo di dimezzamento.
Il tempo di dimezzamento è t½ = [A]0/2k, e dipende da [A]0, dato che le rette di c=f(t) sono rette
46
parallele con diversa intercetta [A]0.
Le reazioni del primo ordine sono generalmente, anche se non necessariamente, quelle che
hanno un solo reagente in quantità unimolecolare (ovviamente, questo sarà il caso se si tratta di
reazioni elementari, dato che ordine e molecolarità sono uguali).
A → B

La velocità della reazione, che può essere definita sia rispetto al reagente A che rispetto al
prodotto P, è data da una legge cinetica del primo ordine rispetto al reagente A:
 v ≡ –(d[A]/dt) ≡ (d[B]/dt) = k[A]
Integrando l’equazione differenziale, detta
sempre [A]0 la concentrazione iniziale del
reagente, avremo:
d [A]
d [A]
= k[A]
= − kdt
dt
[A]
t
[A] d [A]
[A]
= d ln[A] = − k dt
[A]0 [A]
[A]0
0
−
∫
∫
∫
ln[A] = ln[A]0 − kt
[A] = [A]0 e − kt
L’integrale mostra una relazione lineare tra ln[A] e t con
pendenza –k, che rappresenta un primo test per la verifica
della bontà della legge cinetica ipotizzata per la reazione in
esame e consente di ricavare facilmente k. La dimensione di
k è s-1, cioè indipendente dalla dimensione di [A], il che
significa che si può scegliere una qualsiasi unità di misura
per [A] o, anche, diagrammare una qualsiasi grandezza ad
essa correlata.
Per le reazioni del primo ordine il tempo di dimezzamento
sarà:
t1 / 2
ln[A]0
ln[A]
-k
0
1 [A]0 1
[A]0
1
= ln
= ln
= ln 2
k [A] k [A]0 /2 k
t
quindi un valore indipendente da c e, quindi, anche da c0. Nel caso di reazione del primo ordine,
spesso si dà il valore di t½ al posto di k, data la stretta correlazione tra i due.
-
t½ non dipende dalla concentrazione
t½ = 0.693/k
dipende solo da k
è usabile al posto di k per caratterizzare una
reazione di 1° ordine
Vale la pena di ricordare un caso importante di
reazioni del primo ordine e cioè quelle di
decadimento radioattivo, per le quali in particolare il
t½, cioè k (detta in questo caso costante di
decadimento) sono anche indipendenti da T.
47
k = 0.1 s-1
t½ → c = 0.5
tvita → c = 0.37
Un altro parametro particolarmente utile è il tempo di
vita di una specie chimica, che viene definito in
relazione alla cinetica della reazione in cui è coinvolta
come reagente. Per una specie chimica coinvolta in una
reazione del primo ordine, il tempo di vita è definito
come il reciproco della costante cinetica della reazione:
tvita = 1/k. Pertanto, si capisce che è leggermente
superiore a t½ = 0.693/k; ad esempio, per una reazione
del primo ordine con k = 0.1 s–1, si ha:
tvita = 10 s
t½ = 6.93 s
Nel caso di reazioni del secondo ordine si ha:
2A → B
v ≡ -½(d[A]/dt) ≡ (d[B]/dt) = k [A]2
che può essere facilmente integrata, sia per la definizione rispetto ad [A] (in questo caso basta
separare le variabili), che rispetto a B (in questo caso è necessario introdurre il bilancio di materia
per collegare [B] ad [A], riconoscendo che per ogni due molecole di A che reagiscono, se ne forma
una di B, per cui al tempo t si ha [A] = [A]0 – 2x e [B] = x). L’integrazione rispetto ad [A] dà:
1 d [A]
che consente di confrontare i dati sperimentali con la
d [A]
2
−
= k[A]2
−
=
kdt
legge cinetica, diagrammando 1/[A] vs. t, che prevede un
2 dt
[A]2
andamento lineare. Ricordiamo che, in questo caso, l’unità
[A] d [A]
t
di misura di k è M–1 s–1.
−
= 2 k dt
2
[A]0 [A]
0
Per una
1
1
1
1/[A]
=
+ 2kt =
+ kAt
reazione
[A] [A]0
[A]0
del II
ordine si può ricavare il tempo di dimezzamento:
∫
∫
[A] = [A]0/2 a t = t½
t 1/2 = 6.93 s
2k=kA
1/[A]0
I ordine: k = 0.1 s -1
II ordine: kA = 0.1 M-1s-1
0
t 1/2 = 10 s
t
1
1
= 2 kt1 2 +
[A] 0 2
[A] 0
t 1/2 = 20 s
t1 2 =
2
1
= 2 kt1 2
[A]0 [A] 0
1
2 k[A]0
Come si vede, in questo caso t½ dipende dalla
concentrazione iniziale del reagente [A]0. Se
confrontiamo una cinetica del I ordine con una del II ordine, possiamo osservare un aspetto
importante. Come si vede nella figura sopra, per una cinetica del primo ordine il tempo di
dimezzamento, che dipende dalla concentrazione di partenza, diventa sempre maggiore, man
mano che la reazione procede, poiché diminuisce [A]0. Ciò significa che la velocità della reazione
diminuisce più marcatamente di quanto non avvenga per la cinetica del primo ordine, per cui la
reazione va più lentamente a completezza.
48
Per quanto riguarda il tempo di vita, si può facilmente capire che, mentre per la cinetica del I
ordine il tempo di vita era il reciproco di k (infatti, poiché k si misura in s–1, il suo reciproco è
proprio un tempo), per una cinetica del secondo ordine avremo necessariamente tvita = 1/k[A]0. Il
tempo di vita consente di confrontare più facilmente reazioni con cinetiche di ordine diverso.
Naturalmente esistono reazioni del secondo ordine con la partecipazione di due diversi reagenti A
e B, quindi del primo ordine rispetto ad A e del primo ordine rispetto a B.
A+B → P
v ≡ -d[A]/dt = k [A] [B]
Se i due reagenti sono in rapporto stechiometrico ([A]0 = [B]0), l’equazione differenziale è
esattamente uguale al caso precedente: in ogni istante [A] = [B], per cui -d[A]/dt = k [A]2.
Nel caso in cui le due concentrazioni iniziali [A]0 = a0 e [B]0 = b0 non fossero uguali, si avrà:
dx = k (a − x)(b − x)
0
0
dt
dx
= k dt
−
x
)( b0 − x )
0
1
b −x
ln 0
= kt + C
b0 − a0 a0 − x
1
b
ln 0
b0 − a0 a0
1
a (b − x )
ln 0 0
= kt
b0 − a0 b0 (a0 − x )
∫ (a
C=
(a 0 = [A]0 e b 0 = [B]0 )
∫
III.4 Reazioni composite
Finora abbiamo trattato le reazioni nell’ipotesi che ammettano sempre ordine, cioè che sia
possibile esprimere la legge cinetica nella forma:
v = k∏ciνi
e abbiamo già visto che per una reazione elementare (semplice) l’ordine coincide con la
molecolarità ed è perciò sempre intero, mentre un ordine frazionario è indice di reazione
comunque composita.
Una reazione composita è una reazione costituita da più stadi elementari che si possono comporre
in tre modi fondamentali, che possono anche essere variamente combinati tra di loro:
reazioni opposte
R
k
1
→
←
k
P
−1
reazioni consecutive
R
reazioni parallele
R

→
P1

→
P2
P1
P2
Nel caso di reazioni composite si numerano gli steps elementari della successione chimica e le
corrispondenti costanti cinetiche con lo stesso numero; se si hanno reazioni opposte si identificano
le rispettive costanti cinetiche con lo stesso numero, dando il segno + a quella da sx a dx ed il
segno – a quella da dx a sx.
Se si ha una reazione reversibile (in realtà tutte le reazioni sono reversibili per il principio di
micro reversibilità e le costanti cinetiche non sono mai nulle né infinite; peraltro si hanno casi in
cui le costanti cinetiche delle reazioni di ritorno sono molto piccole da poterne trascurare l’effetto
entro gli errori sperimentali), si avrà:
A+B
k
1
→
←
k
−1
che si può anche scrivere come:
49
2C
k
A+B
2C
k
d [A]
= k[A][B]
dt
d [A]
2
la cui velocità è v −1 ≡
= k −1[C]
dt
2C
1
→
la cui velocità è v1 ≡ −
A+B
−1
→
La velocità della reazione complessiva può essere definita in uno qualsiasi dei tre possibili modi
(cioè rispetto ad A, B o C).
v ≡−
d [A]
d [B] 1 d [C]
≡−
≡
dt
dt
2 dt
Se scegliamo di definirla rispetto ad A (ma analogo ragionamento può essere fatto rispetto a B o a
C), si ha:
v =−
d [A]
2
= k1[A][B] − k −1[C] (= v1 − v −1 )
dt
All’equilibrio è v = 0 (le concentrazioni non variano più nel tempo) per cui v1 = v2:
2
[C]e
k
= 1 =K
[A]e [B]e k −1
da cui si vede che K > 0 se k1 > k–1 e viceversa, così come si evidenzia il carattere “dinamico”
dell’equilibrio termodinamico. Naturalmente se siamo in condizioni di equilibrio per lo step in
questione, la concentrazione di qualsiasi
specie può essere espressa in funzione di
quelle delle altre specie e della costante di
[B]e = 0.8 M
equilibrio K, cioè del rapporto k1/k–1.
[B]
[C]
k
Se consideriamo il caso semplice:
all' equilibrio : v = 0 v = v
K =
=
[A][B] k
2
1
1
A
k
1
→
←
k
−1
1
−1
k-1 = 0.02 s
B
-1
−1
in cui si parta dal solo A di concentrazione
iniziale a0, avremo il profilo di concentrazione
variabile in funzione di t, fino al
raggiungimento dell’equilibrio.
In questo caso sarà:
k1 = 0.08 s-1
[A]
[B]e/[A]e = K
[B]e/[A]e = 0.8/0.2 = 4 = k1/k–1
[A] + [B] = a0 = 1
Nel caso di reazioni parallele o competitive, si avrà ad esempio:
k
B
(d[B]/dt) = k1[A]
k
C
(d[C]/dt) = k2[A]
A
1
→
A
2
→
se b0 = c0 = 0, si avrà a0 = [A] + [B] + [C] e:
−
d [A] d [B] d [C]
=
+
= k1[A] + k 2 [A] = ( k1 + k 2 )[A]
dt
dt
dt
[A] = a 0e
− ( k1 + k 2 ) t
ln[A] = ln a 0 - ( k1 + k 2 )t
k = k1 + k 2
50
Il reagente A scompare quindi con una cinetica del I ordine, ma con una velocità complessiva che
è la somma delle due velocità, cioè con una costante di velocità apparente pari alla somma delle
due costanti. Per quanto riguarda i due prodotti, si ricava facilmente che la loro formazione segue
la legge di Wegschneider:
d [C] k1 d [B]
=
=
dt
k 2 d [C]
d [B]
dt
∫
[B]
d [B] =
0
k1
k2
∫
[C]
[B] k1
=
[C] k 2
d [C]
0
legge di Wegschneider
[
[B] + [C] = a 0 − [A] = a 0 1 − e
− ( k1 + k 2 )t
]
Per le reazioni consecutive, consideriamo il caso della reazione A → C, composta da due stadi
irreversibili del primo ordine:
A
−
k
B
1
→
d [A]
= k1[A]
dt
k
2
→
[A] = [A]0 e
C
− k 1t
d [B]
−k t
= k1[A] − k 2 [B] = k1[A]0 e 1 − k 2 [B]
dt
d [C]
= k 2 [B]
dt
Come si vede, il reagente A scompare con la tipica cinetica del primo ordine. Più complessa è la
situazione dell’intermedio B (un intermedio è una specie chimica che si forma durante la
reazione, cioè non fa parte dei reagenti iniziali, e scompare durante la stessa reazione per
trasformarsi nei prodotti finali). Per ricavare l’andamento di [B] = f(t), bisogna risolvere la seconda
equazione differenziale, che è una equazione lineare del primo ordine, per la quale si può usare
come fattore integrante e
k 2t
. Una volta ricavata [B], si ricava facilmente [C] dalla terza equazione
differenziale. Al di là della soluzione
matematica rigorosa, quello che interessa in
questa sede è avere un’idea dell’andamento
-1
k 1 = 0.1 s
[C]
delle concentrazioni delle tre specie chimiche
-1
k2 = 0.1 s
coinvolte in questa reazione.
Come si vede nella figura a fianco, A decresce
con il tipico decadimento del primo ordine.
L’intermedio B si forma rapidamente all’inizio
(quando c’è tanto reagente A), per cui la sua
concentrazione aumenta; successivamente la
[B]
sua
concentrazione
diminuisce
poiché
[A]
continua a formarsi sempre più lentamente
(dato che [A] continua a diminuire), mentre
scompare con una certa velocità (dato che la
sua concentrazione è abbastanza elevata per cui la velocità della seconda reazione è piuttosto
sostenuta). Il prodotto finale C si forma lentamente all’inizio (anzi c’è un tempo di induzione in cui
non si forma affatto, finché [B] non diventa significativo), ma la velocità di formazione aumenta
rapidamente, finché [B] raggiunge il massimo, dopo di che [C] continua ad aumentare, ma la
velocità con cui si forma (la derivata d[C]/dt) diventa sempre più piccola, perché [B] diminuisce.
Si possono avere due situazioni limite: k1 >> k2, in questo caso A si trasforma tutto in B, il quale
lentamente si trasforma in C; in pratica è come se si partisse da B, con la concentrazione iniziale
pari a [A]0, che si trasforma in C con la sua costante cinetica k2.
51
L’altro caso limite si ha quando k2 >> k1.
In questo caso B si forma lentamente,
mentre tende a scomparire velocemente:
di fatto, man mano che si forma,
scompare, per cui la sua concentrazione
rimane molto bassa e sostanzialmente
costante, come mostra la figura.
In questo caso si può ammettere che [B]
sia costante per cui si può scrivere
[C]
k1 = 0.1 s-1
k2 = 1 e10 s-1
k2 >> k1
[A] = [A]0 e − k1t
k1 [A]0 − k1t k1
[B] =
e
= [A]
k2
k2
d[B]/dt = 0
[B]
Questa condizione si definisce stato
stazionario per l’intermedio B e
costituisce una situazione di notevole
semplificazione per trovare la legge
cinetica di una reazione composita. In questo caso, infatti, si può trovare immediatamente
[A]
A → C
v = d [C]
dt
= k 2 [B]
d [B]
= k1[A] − k 2 [B] = 0
dt
[B] =
k1[A]
k2
v = k1[A]
La velocità della reazione risulta esattamente pari alla velocità del primo step, che essendo quello
più lento, risulta essere il cosiddetto rate determining step (rds).
L’applicazione dell’ipotesi dello stato stazionario ad un intermedio I, comporta la seguente
equazione:
∑ν v
d [I]
=
dt
j j
=0
dove νj è il coefficiente con cui l’intermedio I compare nello step j-esimo (con la solita convenzione
che νj è positivo se I è un prodotto, mentre è negativo se I è un reagente) e vj è la velocità dello
step j-esimo.
La semplificazione che viene introdotta dall’applicazione dello stato stazionario ad uno o più
intermedi è notevole, per cui si applica sempre, almeno come prima ipotesi, salvo verificare se la
legge cinetica che si ottiene, descrive adeguatamente i dati sperimentali (in caso negativo, si dovrà
rinunciare alla sua applicazione).
Come esempio consideriamo la seguente reazione
A + B → P
composta dalle seguenti reazioni elementari:
A + B
k
1
→
←
k
C
k
2
→
P
−1
La velocità risulta v ≡ d[P]/dt = k2[C]. La soluzione rigorosa è piuttosto complicata. Applicando
l’ipotesi dello stato stazionario all’intermedio C si ottiene invece
52
d [C]
= k1[A][B] − k −1[C] − k 2 [C] = 0
dt
[C] =
k1[A][B]
k −1 + k 2
d [P]
k k
= k2 [C] = 2 1 [A][B]
dt
k −1 + k 2
v=
L’applicazione dello stato stazionario ad un intermedio (C in questo caso) serve a determinarne la
concentrazione per introdurla nella legge cinetica in cui tale concentrazione compare. Come si è
visto la legge cinetica è stata ottenuta in modo estremamente semplice ed immediato. A questo
punto si può osservare che la legge cinetica può assumere due formulazioni limite:
quando k–1 >> k2
v=
d [P]
k
= k 2 1 [A][B] = k 2 K1[A][B]
dt
k −1
dove K1 è la costante di equilibrio della reazione 1. Questa situazione è definita di “pre-equilibrio”,
poiché la reazione 1 risulta essere sempre in condizioni di equilibrio, dato che la sottrazione di C
per dare il prodotto finale P, è lenta e consente all’equilibrio 1 di riassestarsi in ogni caso.
L’altro caso limite si ha quando k2 >> k–1
v=
d [P]
= k1[A][B]
dt
che è esattamente la velocità dello step 1. Lo step 2 è molto veloce per cui la reazione assume la
stessa velocità dello step 1, che è il rds.
III.5 Effetto della temperatura
La velocità di una reazione chimica è espressa attraverso la costante cinetica k e le concentrazioni
delle specie chimiche che influiscono sulla velocità stessa (generalmente quelle dei reagenti). La
temperatura dunque può influire sulla velocità incidendo sul valore delle concentrazioni, ma questo
effetto è sostanzialmente trascurabile (nel caso di reazioni in fase gassosa, il volume è quello del
reattore che è costante, mentre per le reazioni in soluzione si ha una variazione del volume, ma
poco rilevante). L’effetto sostanziale si ha invece sulla costante cinetica k, per cui quando si vuol
indagare l’effetto della temperatura sulla velocità di una reazione chimica, si deve analizzare la
dipendenza della sua costante cinetica dalla temperatura.
Attualmente viene accettata in modo praticamente generalizzato l’equazione di Arrhenius (1889):
 E 
k = A exp − a 
 RT 
nella quale compaiono due parametri: A, detto fattore pre-esponenziale, ed Ea, detta energia
di attivazione. Secondo la trattazione di Arrhenius i due parametri A ed Ea sono considerati
costanti, il che è vero finché si esplora un intervallo di temperature non troppo esteso, com’è il
caso più frequente, ma non è rigorosamente vero, per cui può succedere di dovere considerare la
dipendenza di Ea e di A da T, quando si abbiano intervalli piuttosto ampi di temperature. Il
riferimento universale all’equazione di Arrhenius è legato, al fatto che dà una buona
rappresentazione dei dati sperimentali, anche se non costituisce il migliore fitting tra le diverse
equazioni empiriche sviluppate alla fine del XIX secolo. Il motivo più rilevante però fu che essa è
basata su una ipotesi di tipo meccanicistico, rivelatasi particolarmente suggestiva e corretta: le
molecole dei reagenti per poter reagire, cioè trasformarsi in prodotti, devono superare una
53
barriera energetica di altezza Ea; d’altra parte esiste un equilibrio tra le molecole con energia
superiore alla soglia e l’insieme delle molecole dei reagenti, cioè l’energia tra le molecole è
distribuita con la legge di Maxwell-Boltzman, che è, appunto, la legge di distribuzione in un
insieme omogeneo in condizioni di equilibrio ad una certa T e p. Con tale ipotesi sia A che Ea
assumono un preciso significato fisico, d’altra parte la stessa equazione è stata dedotta per via
teorica, sulla base delle successive conoscenze chimico-fisiche.
L’andamento previsto dalla Equazione di Arrhenius è il seguente
103/T(103K−1)
Come si vede, Ea > 0 per cui la funzione è sempre crescente con T, inoltre la derivata (d ln k/dT) =
Ea/RT 2, è tanto maggiore quanto maggiore è Ea e quanto più piccola è T. Il concetto che sta alla
base della equazione di Arrhenius, come abbiamo detto, è che le molecole dei reagenti per poter
reagire devono avere una energia superiore a quella media e pertanto non tutte le molecole che
collidono sono in grado di dare prodotti, ma solo quelle che possiedono un sufficiente contenuto
energetico maggiore della media di una quantità Ea.
L’equazione di Arrhenius prevede comunque che la costante di velocità di una reazione aumenti
con la temperatura, per cui ci si aspetta che la velocità di una reazione che ammette ordine
aumenti sempre con la temperatura. Esistono però casi in cui la velocità diminuisce con la
temperatura; in questo caso però si può affermare con sicurezza che si tratta di reazioni composite
(nelle quali è coinvolto un qualche equilibrio esotermico). Infatti, consideriamo il caso della
reazione di ossidazione di NO, che presenta appunto una diminuzione di v con T:
→
2NO + O2
2NO2
la legge cinetica risulta essere la seguente:
v = koss[NO]2[O2]
che potrebbe far pensare ad una reazione elementare, dato che l’ordine corrisponde esattamente
alla molecolarità. Però la velocità decresce con T, il che indica che non può trattarsi di una
reazione elementare, per la quale la velocità deve aumentare con la temperatura.
Il meccanismo di tale reazione è infatti il seguente:
2NO
k
1
→
←
k
N2O2
−1
N2O2 + O2
k
2
→
54
2NO2
per il quale
v = ½{d[NO2]/dt} = k2[N2O2][O2]
Applicando l’ipotesi dello stato stazionario per l’intermedio N2O2
d [N 2 O 2 ]
= 0 = k1[NO]2 − k −1[N 2 O 2 ] − k 2 [N 2O 2 ][O2 ]
dt
k1[NO]2
[N 2 O 2 ] =
k −1 + k 2 [O 2 ]
v=
1 d [NO 2 ]
k k [NO]2 [O 2 ]
= k2 [N 2 O 2 ][O2 ] = 2 1
2 dt
k −1 + k 2 [O 2 ]
Se k–1 >> k2[O2] (condizione di pre-equilibrio) si ha
v=
k1k 2
2
2
2
[O 2 ][NO] = k 2 K c1[O 2 ][NO] = koss [O 2 ][NO]
k −1
koss = k 2 K c1
o
d ln koss d ln k 2 d ln K c1
E
∆U
=
+
= a2 + r 2
dT
dT
dT
RT
RT
La variazione di energia interna, come quella di entalpia, per la reazione reversibile 1, ∆rU o è
senz’altro negativa dato che si tratta di una reazione esotermica (è una reazione di dimerizzazione,
si ha cioè la formazione di un legame chimico, cui corrisponde la liberazione della relativa energia
e la corrispondente diminuzione di energia del sistema). E’ chiaro che, se |∆rU o| > |Ea|, com’è in
questo caso, d ln koss < 0.
TEORIA DELLO STATO DI TRANSIZIONE
Consideriamo la reazione elementare in fase gassosa
A + B
P
la Teoria dello Stato di Transizione (TST) la descrive con il seguente modello, che considera
l’energia interna del sistema.
L’energia interna del sistema (reagenti + prodotti) è descrivibile come una superficie di energia
potenziale. In realtà si tratta di una ipersuperficie in uno spazio multidimensionale, dato che
l’energia dipende dalla posizione reciproca e dalle interazioni di tutti gli atomi che costituiscono il
sistema; pertanto un sistema costituito da n atomi richiede 2n coordinate: n coordinate
generalizzate per la posizione ed n valori del momento della quantità di moto o almeno il valore
della energia interna, cioè almeno n+1 coordinate. Se consideriamo una reazione che coinvolga tre
atomi A, B e C, come ad esempio
A + BC
AB + C
sono necessarie tre coordinate spaziali (ad esempio i tre
vettori distanza rAB, rBC, rAC, oppure due vettori distanza
e l’angolo tra di essi) più il valore dell’energia interna
totale del sistema. Per avere una rappresentazione più
facilmente raffigurabile, possiamo ridurre le quattro
coordinate a tre se fissiamo una coordinata spaziale: ad
esempio supponiamo che l’angolo φ tra i due vettori
55
distanza rAB e rBC sia sempre 180° (cioè i tre atomi siano sempre allineati); in questo caso bastano
le due distanze e l’energia interna totale.
In tal caso l’andamento dell’energia totale
in funzione di rAB e rBC assume la forma di
una superficie come quella rappresentata
nella figura a fianco, con la tipica forma a
sella. La proiezione sul piano orizzontale di
tale superficie, definisce le curve isoipse
dello stesso livello energetico, come
mostra la figura successiva.
Il passaggio
da reagenti
a
prodotti
equivale al
movimento di un punto materiale su questa ipersuperficie di energia
potenziale, partendo dalla locazione che corrisponde allo stato dei
reagenti (cioè l’energia media delle molecole dei reagenti) per
arrivare alla locazione che corrisponde allo stato dei prodotti.
Se consideriamo il caso di due reazioni consecutive la superficie di
energia potenziale (energia interna) ha un andamento del tipo
seguente, dove si vede il passaggio dai reagenti R all’intermedio I,
attraverso il primo stato di transizione (TS), e il passaggio
dall’intermedio I ai prodotti finali P, attraverso un secondo stato di transizione (TS).
Nel fare questo cammino si seguirà il percorso di minima
energia, cioè quello che collega le due locazioni restando
sempre al più basso livello possibile; tale percorso è
denominato MEP (minimun energy path) e corrisponde
sostanzialmente ad un percorso di montagna che attraversa
un passo posto tra la valle dei reagenti e la valle dei
prodotti.
Se consideriamo una particolare coordinata spaziale
generalizzata che descriva il tragitto del MEP (detta
coordinata di
reazione,
c.d.r.), il profilo
energetico
del
MEP lungo la
c.d.r. ha una
forma del tipo
riportato a lato.
Come si può
notare si ha un
massimo
di
energia,
che
corrisponde
al
passo che si
deve superare
per andare dalla
valle
dei
reagenti a quella dei prodotti.
La situazione che si ha in corrispondenza del passo è definita Stato di Transizione e rappresenta
contemporaneamente un massimo per l’energia, rispetto allo stato energetico dei reagenti e dei
prodotti e al cammino possibile per passare dai primi ai secondi, ma è anche un minimo di energia
56
rispetto a tutti gli altri possibili percorsi che portano dai reagenti ai prodotti. Ciò significa che tutti i
legami esistenti nel sistema sono nella propria condizione di equilibrio, quindi di minima energia,
ma ce n’è almeno uno, o comunque quelli coinvolti nella trasformazione chimica, che sono invece
in condizione di massima energia (perché si stanno rompendo o formando). Questa particolare
configurazione atomica del sistema, che si ha in corrispondenza dello Stato di Transizione, viene
denominata complesso attivato, indicato generalmente con X‡ (o X≠): non si tratta di un
intermedio chimico, nel senso che non è una molecola (che, come tale dovrebbe avere tutti i
legami in condizione di minima energia), ma verrà trattato come se lo fosse.
In riferimento al predetto modello, la TST si basa sulle seguenti assunzioni fondamentali:
1) per andare dallo stato iniziale a quello finale occorre attraversare lo Stato di Transizione, cioè
passare sopra il passo
2) il complesso attivato X‡ (che è la particolare aggregazione atomica che si ha allo Stato di
Transizione) è in ogni caso in equilibrio chimico con i reagenti (e con i prodotti quando ci sono)
3) la velocità di reazione è data dal prodotto della concentrazione del complesso attivato per la
frequenza con cui tale specie attraversa il passo relativo allo stato di transizione
Per la reazione elementare
A + B
P
sappiamo che la velocità è data dalla seguente legge cinetica:
v ≡
d [P]
= k [A][B]
dt
secondo la TST, la reazione prevede la formazione del complesso attivato
A + B
X≠
ν≠
→
P
garantendo la condizione di pre-equilibrio la velocità è data da:
v = ν≠ [X≠]
dove ν≠ è appunto la frequenza con cui il complesso attivato si trasforma in prodotti, cioè la
frequenza con cui supera il passo. La concentrazione del complesso attivato può essere ricavata in
base al secondo assunto, attraverso la costante di equilibrio
K TS =
≠
q o≠
X
o o
q Aq B
N A exp (−∆E 0 / RT ) =
[X ] = K TS [A][B] =
q o≠
X
q Aoq Bo
[X ≠ ]
[A][B]
N A exp (−∆E 0 / RT )[A][B]
dove la cos tante di equilibrio è espressa attraverso la termodinamica statistica in funzione delle
funzioni di partizione molecolari per unità di volume q delle specie chimiche coinvolte
nell’equilibrio, e ∆E0 è la differenza tra il livello fondamentale del prodotto X≠ e quello dei reagenti
A e B. La funzione di partizione molecolare è definita come
 ε 
q = exp  − i 
 k BT 
i
dove la sommatoria è estesa a tutti gli stati energetici di energia εi che la specie in questione può
occupare. Di fatto si tratta di un conteggio degli stati quantici accessibili, ponderati per la
probabilità di occupazione espressa dall’esponenziale.
∑
57
La frequenza ν≠ può essere ricavata in due modi diversi, che corrispondono a due possibili
modalità di attraversamento del passo. Una modalità corrisponde ad una particolare vibrazione che
rompe X≠ per dare i prodotti P; in questo caso la frequenza ν≠ è proprio la frequenza di questo
particolare modo normale di vibrazione. Dalla funzione di partizione molecolare per unità di volume
del complesso attivato qX≠ si può estrarre il fattore corrispondente a tale frequenza e lasciare
inalterati gli altri 3N – 1 gradi di libertà. D’altra parte, trattandosi di una vibrazione ampia (che
porta alla rottura di qualche legame), la sua frequenza è bassa per cui il relativo esponenziale può
essere espanso in serie limitandoci al primo termine (e–x ≈ 1 – x):
lim
ν →0
1

1 − exp  − hν

k
T
B 

=
k T
= B
hν

1 − 1 − hν

k
T
B 

1
per cui qX≠ diventa
q
X
≠
=q≠
k T
=q≠ B
1 − exp( −hν ≠ / k BT )
hν ≠
1
di conseguenza la velocità di reazione è
v=
ν ≠ [X ≠ ]
=
ν≠
q o≠
X
q Aoq Bo
N A exp (−∆E 0 / RT )[A][B] =
k T q o≠
k T q o≠
N A exp (−∆E 0 / RT )[A][B] = B
= ν≠ B
N exp (−∆E 0 / RT )[A][B]
h q oq o A
hν ≠ q Aoq Bo
A B
che possiamo confrontare con la legge cinetica prima ricavata
d [P]
= k [A][B]
dt
v ≡
per cui si ricava
k =
k BT q o ≠
N exp ( −∆E 0 / RT )
h q oq o A
A B
Come si può osservare, l’espressione ricavata per la costante cinetica k è molto simile all’equazione
di Arrhenius: in prima istanza si può pensare che l’esponenziale della TST possa corrispondere
all’esponenziale di Arrhenius, per cui si avrebbe
A=
k BT q o ≠
N
h q oq o A
A B
con una dipendenza da T, non troppo marcata, dato che anche le funzioni di partizione molecolare
dipendono da T. A 25 °C kBT/h = 6.212 1012 s−1 (kB = 1.380662 10−23 J K−1; h = 6.62608 10−34 J s).
L’espressione di k in termini di funzioni di partizione molecolare q non è molto agevole, dato che il
loro calcolo non è semplice. Torna utile perciò sviluppare una espressione di tipo termodinamico,
definendo una nuova costante di equilibrio K≠ tra complesso attivato e reagenti
K
≠
k =
=
q o≠
 ∆E 0
N A exp −
o
o
RT
q Aq B

k BT
K
h
≠
k T
≈ B K TS
h
58

 ≈ K TS
che risulta sostanzialmente uguale alla KTS (manca un grado di libertà vibrazionale o traslazionale),
per cui possiamo riferirci alle grandezze termodinamiche standard di attivazione (per semplicità
omettiamo il simbolo dello stato standard, ma è implicito):
∆G ≠ = energia libera standard di attivazione (differenza tra X≠ e reagenti),
∆H ≠ = entalpia standard di attivazione (differenza tra X≠ e reagenti),
∆S ≠ = entropia standard di attivazione (differenza tra X≠ e reagenti).
ricordando che
∆G ≠ = ∆H ≠ − T∆S ≠
e che
RT ln K
≠
= −∆G
≠
(ricordiamo che si tratta di grandezze standard) per cui
≠
k =
k BT − ∆G RT
k T
e
= B
h
h
 − ∆H ≠
e
RT


 ∆S ≠
 e
R






che è nota come equazione di Eyring. Questa equazione ci permette un migliore confronto con
l’equazione di Arrhenius. Ricordiamo che
≠
≠
≠
∆G = − RT ln K = ∆H − T∆S
≠
≠
≠
≠
o
d ln K
∆U
∆H − ∆( pVm )
=
=
2
2
dT
RT
RT
Derivando l’equazione di Arrhenius e l’equazione della TST si ricava rispettivamente:
E
d ln k
=− a
d(1/ T )
R
k =
k BT
K
h
≠
⇒ ln k = ln K ≠ − ln (1 / T ) + ln (k B / h )
d ln k
d ln K ≠ d ln (1 / T ) d ln (k B / h )
=
−
+
d (1 / T ) d (1 / T )
d (1 / T )
d (1 / T )
−
Ea
∆U ≠
=−
−T
R
R
E a = ∆U ≠ + RT = ∆H ≠ − ∆( pV mo ) + RT = ∆H ≠ + 2RT
In questo caso è stata considerata la variazione di volume che accompagna la formazione del
complesso attivato (da due molecole, A+B, ad una X≠).
Nel caso cui non si abbia variazione di volume (reazioni monomolecolari, o reazioni in soluzione),
∆(pVmo) = 0, per cui Ea = ∆H ≠ + RT.
A temperatura ambiente RT ≈ 2.5 kJ mol−1 ≈ 0.6 kcal mol−1, generalmente trascurabile rispetto a
∆H ≠, per cui si può assumere che l’esponenziale entalpico sia sostanzialmente l’esponenziale di
Arrhenius.
Possiamo quindi calcolare il contributo entropico di attivazione, dal valore sperimentale del fattore
pre-esponenziale A di Arrhenius:
k T 
≠
∆S = R ln A − R ln B  − 2 R
 h 
59
oppure diagrammando ln(kh/kBT) vs 1/T, ottenendo −∆H ≠/R come pendenza e ∆S ≠/R come
intercetta.
Per le reazioni in soluzione la situazione è un po’ diversa
perché il meccanismo degli urti avviene in modo diverso: la
frequenza degli urti tra le due molecole D e A in soluzione è
D
minore di quella in fase gassosa, dato che il movimento delle
A
molecole è rallentato dalla presenza del solvente. Ma una volta
che due molecole si sono avvicinate rimangono intrappolate
dal solvente circostante per quello che viene definito effetto
gabbia del solvente. Questo fa si che le due molecole abbiano
D
A
un tempo di contatto molto maggiore di quello in fase
gassosa, per cui possono più facilmente disporsi nella giusta
posizione spaziale per poter reagire (sempre che abbiano
l’energia sufficiente per superare il “passo”). Ciò significa che la velocità della reazione in
soluzione, confrontata con la velocità della stessa reazione in fase gassosa (se tale reazione può
avvenire in entrambe le condizioni), potrebbe essere anche maggiore (ma a volte può risultare
minore o circa uguale).
La velocità di una reazione in soluzione può essere espressa attraverso l’equazione di Eyring, ma
usando un fattore pre-esponenziale adeguato alla frequenza degli urti in soluzione Z.
 ∆G ≠ 
k = Z exp −

 RT 
Per una reazione bimolecolare in soluzione, detti r1 ed r2 i raggi delle due molecole, si ha:
 8π k BT 

Z bi = 
 µ 
1
2
(r1 + r2 )2 ≈ 1011 M −1 s −1
dove µ è la cosiddetta massa ridotta delle due molecole µ = (m1⋅m2)/(m1 + m2).
Mentre per una reazione uni molecolare si ha Zuni (nel caso di una reazione elettrodica di
trasferimento elettronico, che è un esempio di reazione unimolecolare, si usa Zet):
Z uni
k T 
=  B 
 2π m 
1
2
 RT
Z et = 
 2πM



1
2
≈ 103 ÷ 104 cm s −1
60