Codifica di Dati e Istruzioni
‰ Algoritmi
 Istruzioni che
h operano su dati
d
Fondamenti di Informatica
‰ Per scrivere un programma è necessario
rappresentare dati e istruzioni in un formato tale
che l’esecutore automatico sia in grado di
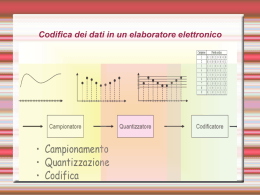
Codifica dell’Informazione


Prof. Francesco Lo Presti
Memorizzare istruzioni e dati
Manipolare istruzioni e dati
Codifica
Codifica dell’Informazione
Sistemi di Codifica
‰ La stessa informazione si può rappresentare in modi
‰ Sistema di codifica (o codifica, o codice)
 Usa un insieme di
d simboli
l di
d base (alfabeto
(alfabeto)
lf
)
 I simboli dell’alfabeto possono essere combinati
ottenendo differenti configurazioni (o codici, o stati),
distinguibili l’una dall’altra
 Associa ogni configurazione ad una particolare entità di
informazione (la configurazione
confi urazione diventa un modo per
rappresentarla)
differenti
diff
ti
11
10
10
9
8
7
6
2
‰ Stesso rappresentazione per informazioni
differenti
italiano
fare,…
inglese
tariffa, prezzo, …
fare
italiano
burro
spagnolo
burro,...
asino, cavalletto, somaro, …
Codifica
3
Codifica
4
Sistema di Codifica: Numeri Interi (Decimali)
Codifica Binaria
‰ Alfabeto
‰ Alfabeto binario: due simboli




Cifre “0”
0 , “1”
1 , “2”
2 , …, “9”
9
separatore decimale (“,”)
separatore delle migliaia (“.”)
Segni positivo ((“+”)
+ ) e negativo ((“-”))
‰ Utilizzata nei sistemi informatici
 Si utilizza una grandezza fisica (luminosità, tensione
elettrica la corrente elettrica),
elettrica,
elettrica) per rappresentare
informazione
‰ Regole di composizione (sintassi)


‰ BIT ((BInary
y digiT)
g )
 unità elementare di informazione rappresentabile con
dispositivi elettronici
Definiscono le combinazioni ben formate
12.318,43
9 123.1.8.43 ?
‰ Codice (semantica)


9 Due
Du ssoli
li stati
st ti
Associano ad ogni configurazione un’entità di informazione
12.318,43 = 1×
1×104+2
+2××103+3
+3××102+ 11××101+1
+1××100+4
+4××10-1+3
+3××10-2

‰ Lo stesso alfabeto può essere usato per codici
cod c diversi
d vers



123,456 = 1×
1×102+ 2
2××101+3
+3××100+4
+4××10-1+5
+5××10-2+6
+6××10-3 [IT]
5
4
3
2
123,456 = 11××10 + 2×
2×10 + 3×
3×10 + 4×
4×10 + 5×
5×101 + 6×
6×100 [UK]
Codifica
con 1 bit si possono rappresentare 2 stati
0/1,, on/off,
ff, si/no
5
Codifica
Codifica Binaria
Esempio di Codifica Binaria
‰ Quanti oggetti/entità si possono codificare con k
‰ Problema: assegnare un codice binario univoco a
bit?





t tti i giorni
tutti
i
id
della
ll settimana
tti
‰ Giorni della settimana: N=7, Ö k≥ log2N Ö k=3
1 bit Ö 2 stati {0,1} Ö 2 oggetti (e.g., Vero, Falso)
2 bit Ö 4 stati {00,01,10,11}
{00 01 10 11} Ö 4 oggetti
3 bit Ö 8 stati {000,001,010,…,111} Ö 8 oggetti
…
K bit Ö2k stati Ö 2k oggetti

C 3 bit,
Con
bit 8 configurazioni
fi
i i
‰ Possibile soluzione
 Lunedì
000
 Martedì
001
 Mercoledì
010
 Giovedì
011
 Venerdì
100
 Sabato
101
 Domenica
110
‰ Quanti bit servono per codificare N oggetti?
 N≤2k Ö k≥ log2 N Ö k= log2 N (intero superiore)
‰ Attenzione: Ipotesi implicita che i codici abbiano
tutti la stessa lunghezza
Codifica
6
7
Codifica
8
Codifica Binaria dei Caratteri: Codice ASCII
Codifica Binaria dei Caratteri: Codice ASCII
‰ Quanti sono gli oggetti compresi nell’insieme?
 26 lettere
l tt r maiuscole/miniscole
m iusc l /minisc l Ö 52
 10 cifre
 ~ 30 segni
g di interpunzione
p
 ~ 30 segni caratteri di controllo {EOF, CR, LF,…}
Ö ~ 120 oggetti Ö k=7
‰ Codice
C di ASCII utilizza
ili
7 bi
bit
 Puo’ rappresentare 27=128 caratteri
‰ Con 8 bit(1 byte) si possono rappresentare 256
caratteri (ASCII esteso)
‰ Si stanno diffondendo codice p
piu’ estesi,, e.g.,
g,
UNICODE, per rappresentare anche i caratteri
delle lingue orientali

UNICODE 16 bit Ö 216=65536 caratteri
UNICODE,
Codifica
9
Codifica
Codifica dei Numeri: Numeri e Numerali
Sistemi di Numerazione
‰ Numero
Numero:: Entita’ Astratta
‰ Posizionali
Posizionali:: Il valore di un simbolo dipende dalla
‰ Numerale
N
Numerale:
l : Sequenza
S
di caratteri
tt i che
h rappresenta
t
posizione
i i
che
h esso occupa all’interno
ll’i t
della
d ll
configurazione.
an-1an-2…a
a0 B
un numero in un dato sistema di numerazione

Lo stesso numero e’
e rappresentato da numerali diversi in
sistemi diversi
9 156 sistema decimale
9 CLVI in numeri romani


‰ Un numerale rappresenta un numero solo se si

specifica un sistema di numerazione


Lo stesso numerale rappresenta diversi numeri in diverse
notazioni
Es: 100100
Differiscono per la scelta della base B
Base indica il numero di simboli usati (0,…,B(0,…,B-1)
Decimale (B=10), Binario (B=2), Ottale (B=8), Esadecimale
(B=16)
‰ Non posizionali:
posizionali: Il valore di un simbolo non dipende
dalla posizione che esso occupa all
all’interno
interno della
configurazione
9 Centomilacento in notazione decimale
9 Trantasei in notazione binaria

Codifica
10
11
Numeri Romani
Codifica
12
Sistemi di Numerazione Posizionale
Conversione BinarioÖ
BinarioÖDecimale
‰ Sistema Decimale:
Decimale: Sistema di Numerazione
‰ an-1an-2…a0 2 Ö an-1*2n-1+…+a1*21+a0*20
Posizionale
P
i i
l in
i b
base B
B=10
10
an-1an-2…a0 10
rappresenta
t
n
1
an-1*10 +…+a1*101+a0*100

‰ 101102 Ö 1*24+0*23+1*22+1*21+0*20=24+22+21=16+4+2=22

Ciascuna cifra
Ci
if rappresenta
t il coefficiente
ffi i t di una potenza
t
della base
Si sommano le potenze di due a cui corrisponde un 1 nel
numerale
l
24 23 22 21 20
16 8
1 0 1 1 0
1 0 1 1 0
4
2 1
‰ Sistema Binario:
Binario: Sistema di Numerazione
Posizionale in base b=2
an-1an-2…a0 2
rappresenta
an-1*2
2n-1+…+a
… a1*2
21+a
a0*2
20
Codifica
13
Codifica
Conversione DecimaleÖ
DecimaleÖBinario
Conversione DecimaleÖ
DecimaleÖBinario
‰ Sistema di Numerazione in base B (B=2 caso particolare)
‰ Il numero binario si ottiene
‰ an-1an-2…a0 B Ö an-1*Bn-1+…+a1*B1+a0*B0=N
N
Ö an-1*Bn-1+…+a1*B+a0=N
‰ Dividendo il numero per la base B
B, si ottiene:
n
2
n
3
‰ an-1*B +an-2*B +…+a1+a0/B


Quozionte: N1=a
N1 an-1*B
Bn-2+a
an-2*B
Bn-3+…+a
a1
Resto:
a0
‰ Il resto della divisione corrisponde all’ultima cifra a0
della
d ll rappresentazione
i
iin b
base B d
dell numero N
‰ Applicando lo stesso procedimento al quoziente N1 si
ottiene la penultima cifra a1 della rappresentazione in
base B
‰ Ripetendo
p
la procedura
p
e’ possibile
p
ottenere tutte le
altre cifre

Ci si ferma quando il quoziente e’ uguale a 0
Codifica
scrivendo la serie dei resti
delle divisioni per 2,
iniziando dall’ultimo resto
ottenuto
tt nut
573:2
286:2
286 2
143:2
71:2
35:2
17:2
8:2
4:2
2:2
1:2
Ö
Ö
Ö
Ö
Ö
Ö
Ö
Ö
Ö
Ö
286
143
71
35
17
8
4
2
1
0
resto 1
resto
t 0
resto 1
resto 1
resto 1
resto 1
resto 0
resto 0
resto 0
resto 1
14
-> a0
-> a1
-> a2
-> a3
-> a4
-> a5
-> a6
-> a7
-> a8
-> a9
10001111012=57310
15
Codifica
16
Intervalli rappresentati
Conversione DecimaleÖ
DecimaleÖBinario
‰ Rappresentando
pp
gli
g interi positivi
p
e lo zero in notazione binaria con
n
18:2=9 resto 0
137:2=68 resto 1
9:2=4 resto 1
68:2=34 resto 0
4:2=2 resto 0
34:2=17 resto 0
2:2=1 resto 0
17:2=8
17:2
8
resto 1
1:2=0 resto 1
8:2=4
resto 0
4:2=2
resto 0
2:2=1
resto 0
12 0
1:2=0
resto
t 1
100102=1810
n cifre (bit) si copre l’intervallo [0, 2 -1]
n
‰ Si sfruttano tutte le 2 disposizioni
Esempio: n=3
0
1
2
3
4
5
6
7
Codifica
17
‰ Per i numerali esadecimali occorrono 16 cifre
18
‰ Conversione esadecimale
esadecimale--binario
{ 0,1,
0 1 …, 9
9,A,B,C,D,E,F
A B C D E F}
A ciascuna cifra esadecimale si fa corrispondere il gruppo di 4 bit
che ne rappresenta il valore
 Esempio
p
F
5
7
A
3
1

‰ Il valore delle cifre

Codifica
Conversioni tra base 16 e base 2
Il sistema esadecimale

000
001
010
011
100
00
101
110
111
NB Anche gli 0 non significativi devono essere rappresentati
100010012=13710

[0,7]
0,1, …, 9 hanno il valore consueto
A vale 10, B vale 11, …, F vale 15
1111 0101 0111
‰ Stesso meccanismo della notazione decimale pesata
1010 0011 0001
‰ Conversione binario
binario--esadecimale
‰ Esempio:
E
i rappresentazione
t i
di BAC16
Partendo da destra si fa corrispondere a ciascun gruppo di 4 o
meno cifre binarie la cifra esadecimale che ne rappresenta il valore

N= 11·16
N
62 + 10·16
0 61 + 12·16
60 = 2988
988
‰ Si usano
s
sspesso
ss st
stringhe
i h esadecimali
s d im li per rappresentare
s t
stringhe binarie
‰ Conversione Decimale Ö Esadecimale?
Rappresentazione più compatta: con sole 2 cifre esadecimali si
rappresentano valori memorizzati in 8 bit
 Esempio: rappresentazione dei colori RGB, indirizzi di memoria,
indirizzi MAC

Codifica
19
Codifica
20
Interi positivi e negativi
Rappresentazione
appr s ntaz on con mo
modulo
u o e ssegno
gno
‰ Per rappresentare un numero con segno, si usa:
‰ Finora abbiamo considerato solamente la
rappresentazione dei numeri positivi (unsigned)
‰ Si utilizzano varie rappresentazioni per gli interi
relativi







‰ Esempio
Modulo e segno
C
Complemento
l
t a1
Complemento a 2
Eccesso
n = 4 bit
5 = 0101
intervallo [[-7,+7]
-5 = 1101
‰ Osservazioni

‰ Per rappresentare gli interi relativi, a parità di

cifre si dimezza l’intervallo dei valori assoluti
Intervallo
I t
ll di rappresentazione
t i
simmetrico
i
t i
Problema: doppia rappresentazione dello zero
9 Ad es. nel caso di 8 bit: 10000000 e 00000000

Codifica
Ulteriore
Ul i
problema:
bl
addizione
ddi i
e sottrazione
i
complicata
li
d
da segno
dei numeri, modulo dei numeri
21
Rappresentazione in complemento a 1
Codifica
22
Rappresentazione
pp
in complemento
p
a2
‰Per i numeri positivi:
positivi: si aggiunge uno 0 a sinistra della
‰ I numeri positivi hanno la stessa rappresentazione che in
rappresentazione
s t i
d
dell numero
m
iin bi
binario
i
‰Es: 5=101 (3 cifre) Ö 0101 (4 cifre)
‰Per
un bit
bi per il segno: 0 per +, 1 per n-1 bit per il modulo
Intervallo di rappresentazione: [[-2n-1+1, +2n-1-1]
complemento a 1
‰ I negativi si ottengono sommando 1 alla loro rappresentazione in
cambiare di segno
g si complementa
p
il numerale bit a bit
complemento a 1
‰ Intervallo di rappresentazione con n bit: [[-2n-1, +2n-1-1]
‰ Notazione Posizionale: Pesi delle cifre: -2n-1 2n-2 ... 21 20
‰ Consideriamo il numero espresso in base 2
xn-1xn-2…x0
‰Es 5= 0101 Ö -5=1010
‰ I numerali positivi iniziano per 0, i negativi per 1
‰ Intervallo di rappresentazione con n bit: [[-2n-1+1,
+1 +2n-1-1]
‰ È una notazione posizionale
Pesi delle cifre: ((--2n-1+1) 2n-2 ... 21 20
Esempio
n = 4 bit
intervallo di rappresentazione [[-7, +7]
5 = 0101
-5 = 1010 ((-7+2)

Il bit più
iù si
significativo
ifi ti xn-1 assume
ss
peso
s negativo
ti -2n-1
‰ Quindi, il valore di un numero N espresso in complemento a 2 è
n-2
Intervallo più esteso ma asimmetrico
i=0
U sola
Una
l rappresentazione
t i
dello
d ll zero
N = -xn-12n-1 + Σ xi 2i
Codifica
23
Codifica
24
Conversione decimaledecimale-binario (CP1 e CP2)
Rappresentazione in complemento a 2 (2)
‰
1.
Esempio:
‰ Abbiamo già visto come fare se il numero X è
‰ Se
S il numero X è negativo
ti :
n = 4 bit
bi
iintervallo
ll [[-8,
8 +7]
7]
510 = 0101CP2
-510 = 1011CP2 (-8+2+1))



Prima regola pratica per complementare (calcolare la
rappresentazione di -X a partire da quella di X):
 Effettuare il complemento di ogni bit di X ed aggiungere 1

28 = 256 < 347 < 512 = 29
intervallo con n bit: [[-2n-1 ,+2n-1-1]
pertanto nmin=10
+347
347 in
i notazione
t i
a 10 bit:
bit
Esempio (4 bit)
9 Complemento
C
l
t di ttutti
tti i bit
bit: 1001
9 Aggiungere 1: 1001+1 = 1010CP2 = -610
-512
- 512
1
Stesso esempio
9 Gli ultimi 2 bit rimangono invariati: __10
9 Complementare gli altri 2 bit: 1010CP2 = -610
Codifica
256
128
64
32
0 1
0
1 0
complementando
l
t d a2
2:
Seconda regola pratica per complementare:
 Partendo da destra si lasciano invariati tutti i bit fino al primo 1
compreso, e poi si complementa bit a bit

Determinare il numero minimo di bit da usare (nmin)
Convertire il valore assoluto di X in notazione a nmin bit
Complementare
l
((a 1 o 2) ill numerale
l cosìì ottenuto
‰ Esempio: convertire ((-347)10 in CP2
9 +610 = 0110CP2
2.
positivo
256
0
128
1
64
0
32
1
16
8
1
16
0
4
1
2
0
8
4
0
1
1
1
2
0
1
1
1
25
Codifica
Rappresentazioni a confronto
Addizioni binarie
Decimale
‰ Le addizioni fra numerali si effettuano cifra a cifra
+7
+6
+5
+4
+3
+2
+1
+0
-0
-1
-2
-3
-4
-5
-6
-7
-8
M&S
0111
0110
0101
0100
0011
0010
0001
0000
1000
1001
1010
1011
1100
1101
1110
1111
-----
CP1
0111
0110
0101
0100
0011
0010
0001
0000
1111
1110
1101
1100
1011
1010
1001
1000
-----
CP2
26
((come iin d
decimale)
i l ) portando
d il riporto
i
alla
ll cifra
if
0+0=0
successiva
0111
0110
0101
0100
0011
0010
0001
0000
----1111
1110
1101
1100
1011
1010
1001
1000
0+1=1
1+0=1
‰ Esempio
1 + 1 = 0 con il riporto di 1
3+2=5
0011 +
0010 =
0101
Se il numero di cifre non permette di rappresentare
il risultato si ha un trabocco (overflow) nella
propagazione
i
d
dell riporto
i
t
Codifica
27
Codifica
28
Aritmetica in CP2: operazione di
negazione
Overflow
‰ Sia A rappresentato in complemento a due
‰ Se si considerano due numeri interi senza segno rappresentati
A = an-1an-2…a1a0
su n bit, si verifica la condizione di overflow ogni volta che il
risultato supera 2n-1
‰ Esempio
Es
i

Sommiamo 5 e 11 su 4 bit (max rappr. =
(5)10 = (0101)2
(11)10 = (1011)2
‰ Abbiamo visto come la rappresentazione di -A si ottiene nel
g
modo seguente:

24-1=15)

Si complementa ogni bit ai ottenendo il bit ai =
Si considera la stringa ottenuta come un intero
senza segno e si somma 1
1 se ai=0
0 se ai=1
‰ Esempio: A=18 su 8 bit

0101+


101 1=
10000

Rappresentazione di A in CP2: 00010010
Complemento (bit a bit): 11101101
Sommiamo 1: 11101101 +
00000001 =
11101110
11101110 = -27 + 26 + 25 + 23 + 22 + 21 = -18
Overflow
Codifica
29
Codifica
Addizioni in complemento a 2
La regola di overflow
‰ L’addizione per interi in complemento a due è identica a
‰ Si verifica un overflow nell’addizione di interi in complemento
p
a
quella per interi senza segno


2 se e solo se
Si somma dal bit meno significativo portando il riporto ad ogni
p
passo
Si trascura l’eventuale riporto in uscita dal bit più significativo


‰ L’unica differenza è nel modo in cui si controlla l’overflow



Sommiamo –3 e 4 su 4 bit
-3 = 1101
1101 +
+4 = 0100


Sommiamo 5 e 4 su 4 bit (max rappr. = 23-1=7)
+5 = 0101
+4 = 0100
0101 +
0100 =
0100 =
10001
L’ultimo bit di riporto viene
ignorato: il risultato è
corretto
Il risultato della somma di due interi positivi è un intero negativo
Il risultato della somma di due interi negativi è un intero positivo
‰ Esempio
‰ Esempio
E
i

30
1001
Overflow: la somma di due interi
positivi non può dare un intero negativo
Codifica
31
Codifica
32
Sottrazioni in complemento a 2
Overflow per la sottrazione
‰ Può verificarsi l’overflow con la sottrazione?
‰ Per sottrarre ad un minuendo (M) un sottraendo (S) basta
sommare M e –S
‰ Conosciamo la maniera semplice di calcolare la negazione di un
numero in complemento a due



‰ Poiché la sottrazione è in effetti implementata


Con una negazione
g
ed una addizione
‰ Vale la regola di overflow della somma
Riusciamo a realizzare la sottrazione come se fosse una somma
Risparmiando così sulla circuteria della ALU

Si verifica se e soltanto se:
9 Il risultato della somma di due interi positivi è un intero negativo
9 Il risultato della somma di due interi negativi è un intero positivo
‰ Esercizio
E
i i

Si!
Calcolare 2 – 5 su 4 bit
Calcolare ((––3)) – 1 su 4 bit
C di i i di overflow
Condizioni
fl
Codifica
33
Esercizio
‰ Calcolare il risultato delle seguenti operazioni binarie tra
numerii iinterii con segno rappresentatii iin complemento
l
a 2 su
8 bit
‰ Scrivere l’equivalente
q
rappresentazione
pp
dei numeri
m
in
decimale (verificando la correttezza del risultato ottenuto)




00001101 + 00111101
00001100 + 10110110
00010100 - 01101111
11110100 + 11101000
Codifica
35
Operazione
A
B
Risultato
<0
A+B
≥0
≥0
A+B
<0
<0
≥0
A-B
≥0
<0
<0
A-B
<0
≥0
≥0
Codifica
34