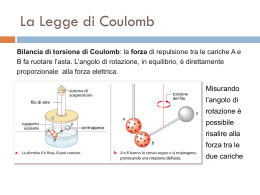
La legge di Coulomb ed il principio di sovrapposizione
Per motivi di natura tecnica risulta molto più semplice misurare con precisione, su scala
macroscopica, la presenza di cariche in movimento piuttosto che quantificare il valore di cariche che stanno
ferme. Pertanto, nel Sistema Internazionale, l’unità di carica non è una grandezza fondamentale, ma derivata
da quella dell’unità di corrente, che misura invece il passaggio di cariche attraverso un conduttore.
Si tratta di un processo al contrario, un po’ come se misurassimo il tempo a partire dalla velocità e dallo
spazio. L’unità di misura che viene così definita prende il nome di Coulomb1 e si indica con la lettera C
maiuscola. Per il momento possiamo dare una definizione alternativa di Coulomb come una carica pari a
quella di: 6.25 × 10
18
elettroni cambiata di segno:
1Coulomb ≡ 6.25 × 1018 elettroni
ma non possiamo giustificare il perché proprio questo numero di elettroni e non un altro. Va detto
comunque che in ogni caso avremmo potuto anche pensare di adottare la carica dell’elettrone come unità di
misura, ma per gli scopi pratici su scala macroscopica essa risulta troppo piccola. Invertendo la definizione
precedente si ha:
− e = −1.6 × 10 −19 C
L’esperienza mostra che due corpi carichi puntiformi, posti nel vuoto a distanza r, interagiscono con una
forza diretta lungo la retta congiungente i due corpi, attrattiva o repulsiva a seconda dei segni delle
reciproche cariche, la cui intensità è tanto maggiore quanto più le cariche
sono vicine e tanto maggiore quanto maggiore è il valore di ciascuna di
q2
esse:
F =k
Con
| q1q2 |
r2
r
q1
q1 e q 2 abbiamo indicato i valori delle rispettive cariche espressi in
Coulomb, ed r ed F sono ovviamente espressi in metri e Newton. k è una costante di proporzionalità che nel
Nm 2
, e le sue unità di misura sono quelle che occorrono per far
Sistema Internazionale vale k = 9 × 109
C2
tornare Newton al primo membro. Rimarchiamo il fatto che la legge sopra esposta, detta legge di Coulomb,
vale esclusivamente per oggetti puntiformi. Un oggetto rigorosamente puntiforme è una entità solo teorica,
tuttavia le particelle elementari possono essere considerate puntiformi, a patto che la distanza r coinvolta
nella legge di Coulomb sia molto grande rispetto alle loro dimensioni.
Una notevole proprietà delle forza elettrica che studieremo, fa sì che la legge di Coulomb valga anche per
oggetti carichi estesi nei quali le cariche siano distribuite con simmetria rigorosamente sferica. Si può
mostrare che se due sfere cariche, poste ad una distanza che permetta di trascurare le possibili variazioni
della distribuzione di cariche sull’una ad opera dell’altra, interagiscono secondo la legge di Coulomb dove al
posto di r andrà inserita la distanza fra i centri2.
Per avere una espressione della legge di Coulomb in termini vettoriali, che contenga cioè anche informazioni
sul verso della forza, dovremo aggiungere il simbolo di un versore r̂1 .
1
Charles Augustin de Coulomb (1736-1806), scienziato francese. A lui si deve la legge che esprime la forza fra due
corpi carichi puntiformi qui esposta, ricavata attraverso un apparato detto bilancia di torsione.
2
Va detto anche che nel momento in cui assumiamo che le cariche siano puntiformi, e che tutte le loro proprietà
possano essere individuate da una grandezza scalare q, anche solo da motivi di simmetria si potrebbe dedurre che la loro
interazione deve essere diretta lungo la congiungente, in quanto in uno spazio vuoto con le sole due cariche in studio,
non si potrebbe definire nessun’altra direzione in modo univoco.
Intenderemo con r̂1 un vettore di modulo 1 orientato dalla prima carica,
q1 verso la seconda q 2 , (cioè sempre
uscente dalla carica della quale si vuol esprimere la forza da essa esercitata) ed eliminando il modulo, si ottiene:
qq
F21 = k 1 22 ˆ
r1
r
forza esercitata su q2 da q1
La formula ora fornisce, oltre all’intensità, anche la direzione della forza che la carica q1 esercita su q2 .
Precisamente, se le due cariche hanno lo stesso segno , cioè se q1q2 > 0 , allora q1 esercita su q2 una forza che
ha direzione r̂1 , cioè uscente da q1 e quindi repulsiva. Se invece q1q2 < 0 , cioè le due cariche hanno segno
diverso, allora q1 esercita su q2 una forza che ha direzione −rˆ1 , cioè entrante in q1 e quindi attrattiva.
Si noti che F21 va pensata applicata su q2 mentre F12
Q2
Q1
applicata su q1 , come si vede in figura. Riflettere anche
F12
sul fatto che, a norma del principio di azione e reazione, è
sempre e comunque F12 = −F21 anche se q1 e q2 sono
molto differenti in valore.
Q1
F12
F
F21
Q2
21
Allo
scopo
di
semplificare
alcune
formule
dell’elettromagnetismo, si paga il piccolo prezzo di
complicare un pochino l’espressione della legge di
Coulomb, ponendo al posto di k l’espressione:
k=
il che è sempre possibile, ricordando che k = 9 × 109
ε0 =
F12
Q1
Q2
F21
1
4πε0
Nm 2
, purché si ponga
C2
1
C2
= 8.85 × 10−12
9
4π × 9 × 10
Nm 2
valore che viene detto costante dielettrica del vuoto. La legge di Coulomb assume così la nuova forma:
F =
1 | q1q2 |
4πε0 r 2
A completamento di quanto detto va enunciata l’altra fondamentale proprietà dell’interazione elettrica, che
va sotto il nome di principio di sovrapposizione.
Nel caso in cui si avesse a che fare con tre o più cariche puntiformi, vincolate a stare in prefissate posizioni, ci
si potrebbe chiedere se la presenza di q 3 accanto a q1 e q2 impedisca di utilizzare la legge di Coulomb nella
stessa forma, o per dire meglio dire in che modo q 3 modifica la forza che le altre due si scambiano quando
essa non c’è.
L’esperienza mostra che vale una regola additiva degli effetti: la forza che q2 e q 3 esercitano su q1 è pari alla
somma vettoriale delle forze che q2 eserciterebbe su q1 come se q 3 non ci fosse, e della forza che q 3
eserciterebbe su q1 come se q2 non ci fosse.
PRINCIPIO DI SOVRAPPOSIZIONE: IN UN INSIEME DI TRE O PIÙ CARICHE PUNTIFORMI, LA FORZA CON LA QUALE
INTERAGISCONO DUE QUALUNQUE DI LORO PUÒ ESSERE CALCOLATA COME SE LE ALTRE NON CI FOSSERO, E LA
FORZA RISULTANTE SU UNA QUALUNQUE DI ESSE È LA SOMMA VETTORIALE DI TUTTE LE FORZE CALCOLATE IN
QUESTO MODO.
Esercizio
Tre cariche puntiformi sono vincolate ai vertici di un triangolo
rettangolo i cui cateti misurano 3.0 cm ciascuno, come in figura. I
valori delle cariche sono:
Q1 = 2.5 × 10−6 C = 2.5 μC
Q2 = −4.0 × 10−6 C = −4.0 μC
Q2
F23
F21
Q3 = 5.2 × 10−6 C = 5.2 μC .
Calcolare l’intensità ed individuare la direzione della forza che
complessivamente le altre cariche esercitano su Q2 .
Q1
Q3
Risposta:
Per il principio di sovrapposizione la carica Q2 subisce la forza F21 attrattiva da parte di Q1 come se
Q3 non ci fosse, e la forza attrattiva F23 di Q3 come se Q1 non ci fosse. Le loro intensità valgono:
| F21 |=
−6
× (−4.0 × 10−6 ) |
1 | Q1Q2 |
9 | 2.5 × 10
=
9.0
×
10
= 10 × 109−6−6+4 N = 100 N
−2 2
4πε0 r 2
(3.0 × 10 )
| F23 |=
−6
× 5.2 × 10−6 |
1 | Q2Q3 |
9 | −4.0 × 10
=
9.0
×
10
= 10.4 × 109−6−6+4 N = 104 N
2
2
2
−
−
2
2
4πε0 r
(3.0 × 10 ) + (3.0 × 10 )
La forza risultante F è rappresentata in direzione ed intensità dalla
diagonale del parallelogramma che ammette F21 e F23 come lati. Vi sono
due vie per il calcolo.
Q2
α
F23
F21
1) Dal teorema di Carnot si ricava:
| F |2 =| F21 |2 + | F23 |2 −2 | F21 || F23 | cos(π − α)
π
otteniamo:
ed essendo α =
4
3
| F |2 = 1002 + 1042 − 2 ⋅ 100 ⋅ 104 ⋅ cos π
4
da cui | F |= 189 N
2) Calcoliamo le componenti x ed y di ciascuna delle due componenti:
Q1
π −α
Q2
F21x = 0 N , F21y = −100 N
F23x
F23y
π
2
= F23 cos = 104
= 73.5 N
4
2
π
2
= − F23 sin = −104
= −73.5 N
4
2
Sommandole otteniamo le componenti della risultante:
Q3
F
F21
Q1
π
4
F23
Q3
Fx = F12x + F23x = 0 N + 73.5 N = 73.5 N
Fy = F21y + F23y = −110 N - 84.9 N = −174 N
Q2
ˆ
73.5 x
dal teorema di Pitagora si ha il modulo si F :
ˆ
− 174 y
F = Fx2 + Fy2 = 73.52 + (−174)2 = 35678 = 189 N
Per direzione di F si intende l’angolo ϑ (theta) che il rappresentante del vettore F applicato
nell’origine forma con l’asse orientato delle ascisse. Come si vede dalla figura, le lunghezze delle
componenti di F sono cateto opposto ed adiacente del triangolo rettangolo che ha proprio F come
ipotenusa. Il loro rapporto, compreso il segno dà il valore della
tangente di ϑ :
ˆ
73.5 x
tan ϑ =
−174
= −2.37
73.5
⇒
ϑ
ϑ = arctan (−2.37) = −67.1°
ˆ
− 174 y
Si faccia attenzione che la funzione tan−1 della calcolatrice corrisponde
all’arcotangente e quindi restituisce sempre un angolo compreso fra
−90° e +90° . Solo un ragionamento sulla figura permette di capire se
il valore di ϑ richiesto dal problema è esterno all’intervallo di questi
valori.
A titolo di esempio si supponga di dover calcolare la direzione del
vettore in figura. Risulta ancora
tan ϑ =
174
= −2.37
−73.5
ˆ
174 y
Tuttavia il valore tan−1(−2.30) = −66.5° che fornisce la calcolatrice non
ϑ
è la risposta corretta. Un’analisi della figura fa capire che è:
ϑ = 180° + arctan (−2.37 ) = 180° − 67.1° = 113°
Studiare Walker p6-7; pp9-12
Es.p E38 n18, 19
− 73.5 xˆ