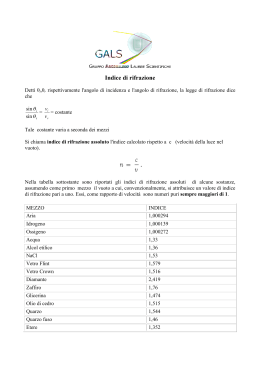
Misura dell’indice di rifrazione relativo dell’acqua rispetto all’aria mediante immagini
digitali
Introduzione
Quando la luce incide perpendicolarmente alla superficie di separazione tra le due sostanze, ad
esempio acqua ed aria, il fascio l’attraversa indisturbato, proseguendo nell’aria senza alcun cambio
di direzione. Se, invece, il fascio incide sulla superficie di separazione con certo angolo, una parte
della luce del fascio viene riflessa ed una parte viene invece rifratta, ossia attraversa la superficie
di separazione cambiando la direzione di propagazione (Figura 1).
Figura 1
Nello schema di Figura 1 un fascetto si propaga dall’acqua all’aria, quindi si dirà che esso incide
sull’interfaccia acqua-aria. Si chiama angolo di incidenza l’angolo formato dalla retta che
rappresenta la direzione di propagazione del fascetto incidente nel primo mezzo (in questo caso
l’acqua) con la retta perpendicolare all’interfaccia stessa. In Figura 1 l’angolo di incidenza è indicato
con il simbolo θi. Si chiama angolo di riflessione l’angolo formato dalla retta che rappresenta la
direzione di propagazione del fascetto riflesso (cioè dopo aver incontrato l’interfaccia) con la retta
perpendicolare all’interfaccia stessa. In Figura 1 l’angolo di riflessione è indicato con il simbolo θr.
Si chiama angolo di rifrazione l’angolo formato dalla retta che rappresenta la direzione di
propagazione del fascetto rifratto nel secondo mezzo (in questo caso l’aria) con la retta
perpendicolare all’interfaccia stessa. In Figura 1 l’angolo di rifrazione è indicato con il simbolo θ’r.
Sperimentalente si osserva che:
- quando la luce è riflessa, gli angoli di incidenza e di riflessione sono uguali, cioè
θi = θ r
- il fascetto rifratto e il raggio riflesso formano con la perpendicolare all’interfaccia angoli di
incidenza e rifrazione tali che (legge di Snell)
sin (θ i )
= n1,2 
sin (θ 'r )
dove n1,2 è una costante che dipende da entrambe le sostanze o materiali. In particolare si definisce
n
n1,2 ≡ 2
n1
dove n1 e n2 sono detti indici di rifrazione delle sostanze in cui si propagano rispettivamente il
fascetto incidente ed il fascetto rifratto. Nel caso particolare in figura, il fascetto incidente si
propagava in acqua mentre il fascetto rifratto in aria: si può determinare sperimentalmente che in
questo caso n1 = nacqua ≅ 1.33 e n2 = naria ≅ 1 .
In conseguenza della legge di Snell, quando la luce passa da un mezzo con indice di rifrazione
minore a un mezzo di indice di rifrazione maggiore, il raggio rifratto si avvicina alla perpendicolare
all’interfaccia, mentre se la luce passa da un mezzo di indice di rifrazione maggiore ad uno minore,
si allontana dalla perpendicolare all’interfaccia. Quando la luce passa da una sostanza o materiale
con indice di rifrazione maggiore ad uno minore, come nel caso della Figura 1, il più piccolo angolo
di incidenza per cui non si ha più rifrazione si chiama angolo limite. In tali casi poiché il fascetto
rifratto si allontana dalla normale, esso arriverà ad un valore di 90° oltre il quale non esisterà più il
fascetto rifratto e tutta la luce si rifletterà nuovamente nella sostanza o materiale in cui si propagava
il fascetto incidente. L’esistenza dell’angolo limite è legata al fatto che, dalla legge di Snell
introdotta sopra, è possibile trovare dei valori di θi per il quali l’angolo di rifrazione θ 'r è tale che:
n1
sin (θi ) ≥ 1 
n2
Il più piccolo di questi valori, quando θ 'r = 90°, detto appunto θl , è quindi quello per cui:
sin (θ l ) =
n2
.
n1
Nel caso in esame, n1 = nacqua ≅ 1.33 , n2 = naria ≅ 1 e θl ≅ 48,75°. Quindi, per avere riflessione
totale, un fascetto deve propagarsi da una sostanza con un dato indice di rifrazione ad un’altra con
indice di rifrazione minore. Il fenomeno della riflessione totale permette di condurre la luce da un
luogo all’altra seguendo percorsi non rettilinei (come nelle fibre ottiche).
Misura dell’indice di rifrazione mediante foto digitali
Un tipico percorso di un fascio incidente e rifratto (laser rosso, lunghezza d’onda circa 632 nm) è
mostrato in Figura 2. Il fascetto si propaga dal basso verso l’alto, da acqua ad aria. Mediante un
software di Geometria dinamica (es. Cabrì o Geogebra) è possibile approssimare la traiettoria del
fascetto in acqua ed in aria e determinare gli angoli di riflessione e rifrazione.
Figura 2
Il procedimento è il seguente. Si individua la retta w che rappresenta lo spigolo visibile del piano
che rappresenta l’interfaccia acqua-aria. Quindi, si fa passare una retta perpendicolare z a w
passante per il punto P in cui il fascetto viene rifratto (Figura 3).
Figura 3
A questo punto si tracciano due segmenti (in giallo, EP e PF, Figura 4) in modo da sovrapporli al
fascetto incidente e rifratto, cercando di approssimare al meglio la loro completa traiettoria.
Figura 4
Infine si individuano gli angoli di incidenza e di rifrazione (Figura 5). Per individuare l’angolo di
incidenza è sufficiente individuare un punto sul segmento PE (T), un punto sull’asse z di quota
minore di P (S) e P come vertice. Si procede in modo analogo per individuare l’angolo di rifrazione
(usando i punti R, Q e P come vertice)
Figura 5
Utilizzando la funzione “Misura” di Cabrì (o equivalente in GeoGebra) è possibile determinare il
valore degli angoli di incidenza e rifrazione. Utilizzando più foto è possibile costruire una tabella
degli angoli di incidenza e rifrazione e dei relativi seni e verificare se i punti sono allineati. Quindi,
ricavare un fit lineare dei dati del tipo
sin (θ r ) = a sin (θi ) + b .
Il parametro b dovrebbe essere compatibile con zero; il coefficiente angolare a restituisce una stima
dell’indice di rifrazione dell’acqua rispetto alla aria (circa 1.33).
N.B. Se possibile, si consiglia di ricavare per ogni foto più valori degli angoli di riflessione e
rifrazione per diminuire l’effetto di possibili errori dovuti ad una non corretta individuazione della
superficie dell’acqua o del punto di in cui avviene la rifrazione. Tali errori possono essere dovuti
alla qualità della foto e alla risoluzione dello schermo.