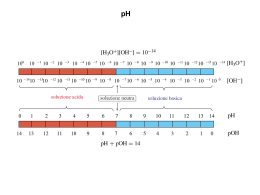
EQUILIBRI ACIDO-BASE
Dissociazione di un acido forte in acqua:
←
HCl(g) + H2O(l)
Cl- (aq) + H3O + (aq)
→
ione idronio
La reazione viene spesso
scritta in forma semplificata:
←
HCl(g)
Cl- (aq) + H+ (aq)
→
H+ di per sé (protone libero!) non è presente in soluzione:
è una notazione semplificata per rappresentare lo ione
idronio (o specie omologhe).
1
HCl è un acido forte: in acqua è (all’atto pratico) completamente
dissociato in ioni.
Principali acidi forti: HCl, HBr, HI, HNO3 , HClO 4
Acidi deboli: sono solo parzialmente dissociati in acqua:
Acido acetico come esempio di acido debole
HAc ≡ CH3 − C
O
O −H
Reazione di dissociazione:
←
HAc(aq) + H2O(l)
Ac - (aq) + H3O + (aq)
→
Rappresentazione sintetica:
HAc
←
→
Ac - + H+
2
Costante di dissociazione acida: costante di equilibrio per
la reazione di dissociazione
aH aAc [H+ ] [Ac - ]
Ka =
=
= 1,75 × 10 −5 a 25°C
aHAc
[HAc]
+
-
Nota: con la notazione completa della reazione di
dissociazione risulterebbe un forma diversa della costante di
equilibrio, ma equivalente se aH O(l) = 1
aH O (aq) aAc (aq) [H+ ] [Ac - ]
Ka =
=
aHAc(aq) aH O(l)
[HAc]
2
+
-
3
2
Gli acidi carbossilici R − C
O
sono acidi deboli con una
O −H
costante di dissociazione acida dipendente da R.
3
NaOH(s) come esempio di base forte: si scioglie in acqua
dissociandosi completamente (all’atto pratico) in ioni
←
NaOH(s)
Na + (aq) + OH− (aq)
→
ione idrossido
Principali basi forti: LiOH, NaOH, KOH, RbOH, CsOH
Basi deboli: dissociazione parziale.
Esempio dell’ammoniaca:
NH3 (aq) + H2O(l)
←
+
NH4 (aq) + OH− (aq)
→
Costante di idrolisi basica: costante di equilibrio per la
reazione di dissociazione basica
aNH (aq) aOH (aq) [NH + ] [OH- ]
4
Kb =
=
= 1,75 × 10 −5 a 25°C
aNH (aq) aH O(l)
[NH3 ]
+
-
4
3
2
4
Ammine organiche sono basi deboli
R − NH2
R − NH − R'
R"
R − N − R'
Finora si è implicitamente usata la definizione secondo
Arrhenius di acido/base:
Acido: sostanza che in acqua libera ioni H3O +
Base: sostanza che in acqua libera ioni OHE’ preferibile la definizione secondo Bronsted-Lowry che fa
riferimento alla sola capacità di accettare/donare protoni
HAc = specie acida: può donare protoni a H2O
Ac - = specie basica: può accettare protoni da H3O +
←
HAc + H2O
Ac + H3O +
→
acido
base
base
acido
HAc / Ac - coppia coniugata acido / base
5
+
NH3
base
H2O
acido
←
→
+
NH4
acido
+
OH−
base
NH4 + / NH3 coppia coniugata acido / base
L’acqua H2O può comportarsi sia da acido (donando protoni e
trasformandosi in OH- ) che da base (acquisendo protoni
trasformandosi in H3O +)
Reazione di autoprotolisi dell’acqua: reagisce sia da acido
che da base
←
H2O + H2O
H3O + + OH−
→
K w : costante di autoprotolisi dell’acqua (water)
aH O (aq) aOH (aq)
+
−14
Kw =
=
[H
]
[OH
]
=
1
,
00
×
10
a 25°C
2
aH O(l)
+
-
3
2
Reazione semplificata: H2O
←
→
H+ + OH−
6
7
A ciascuna coppia coniugata acido / base corrisponde una
coppia di costanti K a / K b
HA
A - + H2O
HA + A + H2O
-
H2O
←
→
←
→
←
A - + H+
→
←
HA + OH→
+
[A - ][H+ ]
Ka =
[AH]
+
Kb =
[HA][OH- ]
[A - ]
A + H + HA + OH K aK b =
-
H
+
-
+ OH
-
×
[A - ][H+ ][HA][OH- ]
-
[AH][A ]
=
= [H+ ][OH- ] = K w
Principio generale: alla “somma” di reazioni corrisponde il
prodotto delle costanti di equilibrio.
8
Scala logaritmica delle costanti di equilibrio: pK := − log K
pK w = − log K w = − log( K a K b ) = − log( K a ) − log( K b ) = pK a + pK b
pK w = 14,00 a 25°C
Relazione tra le costanti di equilibrio di una coppia coniugata
acido/base:
K a Kb = K w
pK a + pK b = pK w
9
pH
pH := − log aH O = − log[H+ ]
[H+ ] = 10 − pH
+
3
K w determina la concentrazione [OH- ] per un dato pH
−14
K
1
,
00
×
10
−(14 − pH )
a 25°C : [OH- ] = +w =
=
1
,
00
×
10
[H ]
10 − pH
[H+ ] = 1,00 × 10 −3 M
pH = 3,00
[OH- ] = 1.00 × 10 −11
[H+ ] = 3,12 × 10 −3 M
pH = 2,51
[OH- ] = 3,21 × 10 −12
[H+ ] = 1,00 × 10 − 2 M
pH = 2,00
[OH- ] = 1.00 × 10 −12
A 25°C:
Soluzione neutra : [H+ ] = [OH− ] = 10 −7
Soluzione acida : [H+ ] > 10 −7
Soluzione basica : [H+ ] < 10 −7
pH = 7
[OH− ] < 10 −7
[OH− ] > 10 −7
pH < 7
pH > 7
10
pH di soluzioni (in acqua) di acidi forti
Problema: quant’è il pH di una soluzione 0,065 M di HCl?
Approssimazione: trascuriamo il contributo dell’autoprotolisi
dell’acqua.
F = concentrazione Formale di HCl = 0,065 M
[H+ ] = [Cl- ] = F
pH = − log F = 1,19
Questione: quando tale valore di pH è corretto e quando è
sbagliato?
Bisogna valutare il contributo dell’autoprotolisi dell’acqua!
11
Analisi completa tenendo conto dell’autoprotolisi dell’acqua
Concentrazioni incognite : [H+ ], [OH- ], [Cl- ]
Sono necessarie 3 equazioni:
1) Stechiomet ria : [Cl- ] = F
2) Equilibrio di autoprotol isi : K w = [H+ ][OH- ]
3) Elettroneu tralità : [H+ ] = [Cl- ] + [OH- ]
x = [H+ ]
K w = x( x − F )
[Cl- ] = F
⇒
[OH- ] = [H+ ] - [Cl- ] = x − F
x 2 − Fx − K w = 0
F ± F 2 + 4Kw
Soluzione equazione di secondo grado : x =
2
12
F ± F 2 + 4Kw
x=
2
Radice positiva :
quale radice?
2
F
+
F
+ 4Kw
+
x = [H ] =
2
Casi limite:
1) F >> K w = 10 −7 M
F 2 + 4Kw ≅ F 2
[H+ ] = F , pH = − log F
⇒
stesso risultato considerando solo il contributo dell’acido al pH!
2) F << K w = 10 −7 M
F + 4Kw ≅ 4Kw
2
⇒
F + 2 Kw
[H ] ≅
≅ K w , pH = 7
2
+
contributo trascurabile dell’acido al pH !
13
pH
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
pH = pF
pH = 7
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
= − log F
pF
Conclusioni:
1) F ≤ 10 −8
: pH indipendente dalla presenza dell’acido
2) 10 −8 < F < 10 −6 : soluzione completa del problema
3)
: si può trascurare l’autoprolisi dell’acqua 14
10 −6 ≤ F
pH di soluzioni (in acqua) di basi forti
Problema: quant’è il pH di una soluzione di NaOH a molarità F ?
Analisi completa tenendo conto dell’autoprotolisi dell’acqua
Concentrazioni incognite : [H+ ], [OH- ], [Na + ]
Sono necessarie 3 equazioni:
1) Stechiomet ria : [Na + ] = F
2) Equilibrio di autoprotol isi : K w = [H+ ][OH- ]
3) Elettroneu tralità : [H+ ] + [Na + ] = [OH- ]
y = [OH− ]
Kw = ( y − F ) y
[Na + ] = F
⇒
[H+ ] = [OH− ] - [Na + ] = y − F
y 2 − Fy − K w = 0
Stessa equazione algebrica del problema dell’acido forte!
15
F ± F 2 + 4Kw
Soluzioni equazione di secondo grado : y =
2
2
F
+
F
+ 4Kw
Radice positiva :
y = [OH ] =
2
K
2Kw
[H+ ] = w =
y
F + F 2 + 4Kw
Casi limite:
1) F >> K w = 10 −7 M
F 2 + 4 K w ≅ F 2 ⇒ y = [OH- ] = F ,
[H+ ] =
2) F << K w = 10 −7 M
F 2 + 4Kw ≅ 4Kw
contributo trascurabile
della base al pH !
⇒
Kw
Kw
=
, pH = 14 + log F
[OH ] F
y = [OH− ] ≅
[H+ ] =
F + 2 Kw
≅ Kw ,
2
Kw
= Kw ,
−
[OH ]
pH = 7
16
pH
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
pH = 14 − pF
0
1
2
3
4
5
6
7
8
9 10 11 12 13 14
pF
17
pH della soluzione a molarità (formale) F dell’acido debole HA
← +
[H+ ][A - ]
HA
H + A
Ka =
→
[HA]
1) Quant’è l’acidità della soluzione?
2) Quanto è dissociato?
Analisi nell’ipotesi di un contributo trascurabile da parte
dell’autoprotolisi dell’acqua.
Concentrazioni incognite : [H+ ], [A - ], [HA]
Sono necessarie 3 equazioni:
1) Stechiomet ria : [HA] + [A - ] = F
[H+ ][A - ]
2) Equilibrio di dissociazione : K a =
[HA]
3) Elettroneu tralità : [H+ ] = [A - ]
18
x = [H+ ] = [A - ]
[HA] = F − x
x2
Ka =
F−x
2
x
+ Ka x − Ka F = 0
Equazione algebrica del secondo ordine:
2
−
K
+
K
+
a
a + 4Ka F
Radice positiva : [H ] = [A ] = x =
2
Esercizio: in una soluzione 0,0200 M di acido benzoico
−5
avente K a = 6 ,28 × 10 , quant’e il pH e quant’è la frazione
di acido dissociato?
K a 2 + 4 K a F = 0,002242
x = 0,001090
pH = − log 0,001090 = 2,963
[A - ]
x
= = 0,054 ⇒ 5,4%
[A ] + [HA] F
19
Frazione di dissociazione α = parte dell’acido dissociata
[A - ]
x
=
α := [A ] + [HA] F
(1 − α ) è la parte indissociata dell' acido
x2 Ka x Ka
1
2 α
+
−
=
+
−
=0
α
2
F F F
r r
F
rα + α − 1 = 0
2
r :=
F
Ka
1 + 4r − 1
α=
2r
+
Il pH è determinato dal grado di dissociazione: [H ] = [A ] = αF
20
21
α
F = 2Ka
1
0,9
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0
-3
-2,5
-2
-1,5
-1
-0,5
0
0,5
1
1,5
2
F
− log r = − log
Ka
22
r ≡ F / Ka
Casi particolari:
1) Acido semi - dissociato per r = 2 :
α = 1/ 2
F = 2Ka
[H+ ] = αF = K a
2) Acido poco dissociato per r >> 2 :
pH = pK a
F >> 2 K a
1 + 4r − 1
4r − 1 1
≅
≅
<< 1
2r
2r
r
1
1
[H+ ] = Fα ≅ F r = K a F
pH = pK a − log F
2
2
3)Acido dissociato quasi completame nte per r << 2 : F << 2 K a
α=
r →0:
rα 2 + α − 1 ≅ α − 1 = 0 ⇒ α ≅ 1
[H+ ] = Fα ≅ F
pH ≅ − log F
Se F << 10 −7 l' acido non contribuisce al pH della soluzione
23
pK a = 4
α ≈1
α ≈0
6
pH ≈ pF
pH ≈ pK a / 2 + pF / 2
pH
5
4
3
2
1
0
0
1
2
3
4
pK a
5
6
pF = − log F
24
Se K a > 10 ( pK a < −1) , per concentrazioni significative
(F<1M) , l’acido è completamente dissociato all’atto pratico
F
r=
<< 1 :
α ≅1
Ka
Acido forte = acido con K a elevata
25
pH della soluzione a molarità (formale) F della base debole B
← +
BOH
B + OH→
[B + ][OH- ]
Kb =
[BOH]
Analisi nell’ipotesi di un contributo trascurabile da parte
dell’autoprotolisi dell’acqua.
Concentrazioni incognite : [OH− ], [B + ], [BOH]
Sono necessarie 3 equazioni:
1) Stechiomet ria : [BOH] + [B + ] = F
[B + ][OH- ]
2) Equilibrio di dissociazione : K b =
[BOH]
3) Elettroneu tralità : [B + ] = [OH- ]
−
+
y = [OH ] = [B ]
[BOH] = F − y
y2
Kb =
F−y
26
2
Equazione algebrica del secondo ordine: y + K b y − K b F = 0
Kb + 4 Kb F − Kb
−
+
Radice positiva : [OH ] = [B ] = y =
2
[B + ]
y
:
=
=
α
Frazione di dissociazione della base:
[B + ] + [BOH] F
2
r :=
F
Kb
[H+ ] =
rα 2 + α − 1 = 0
Kw
Kw
=
[OH- ] α F
α=
1 + 4r − 1
2r
pH = pK w − log α − log F
27
r ≡ F / Kb
Casi particolari:
1) Base semi - dissociata :
α = 1/ 2
r=2
[H+ ] = K w / K b
2) Base poco dissociata : r >> 2
1
α≅
<< 1
r
Kw
Kw
[H ] =
≅
Fα
Kb F
+
F = 2 Kb
pH = pK w − pK b
F >> 2 K b
1
1
pH = pK w − pK b − pF
2
2
3) Base dissociata quasi completame nte : r << 2 F << 2 K b
α ≅1
[H+ ] =
Kw Kw
≅
Fα
F
pH ≅ pK w − pF
Se F << 10 −7 la base non contribuisce al pH della soluzione
28
pK b = 4
pH
α ≈0
α ≈1
pH ≈ 14 − pK b / 2 −
pH ≈ 14 − pF
− pF / 2
14
13
12
11
10
9
8
7
0
1
2
3
4
pK b
5
6
pF = − log F
29
Se K b > 10 ( pK b < −1) , per concentrazioni significative
(F<1M) , la base è completamente dissociato all’atto pratico
F
r=
<< 1 :
α ≅1
Kb
Base forte = base con K b elevata
30
Esercizio: in una soluzione 0,0200 M di benzoato di sodio
−5
K
=
6
,
28
×
10
(acido benzoico: a
) quant’e il pH e quant’è la
frazione di acido indissociato?
Ione benzoato: base debole coniugato all’acido benzoico
+
←
[A
][H
]
+
HA
A + H
Ka =
= 6 ,28 × 10 −5
→
[AH]
A + H2O
-
←
→
HA + OH
-
[HA][OH- ] K w
−10
Kb =
=
=
1
,
59
×
10
Ka
[A - ]
[HA]
BOH → A
B → HA
α=
F
pF = − log 0,02 = 1,699 << pK b = 9,799
-
+
pH ≈ 14 − pK b / 2 − pF / 2 = 8,251
α ≅ K b F = 8,92 × 10 −5
31