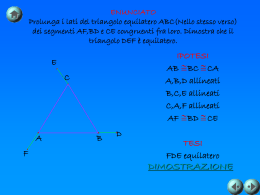
Teorema
Enunciato
• Sui prolungamenti della base AB di un triangolo
isoscele ABC si considerino i due segmenti
congruenti AD e BE.
• Dimostrare che il triangolo DEC è isoscele.
Dimostrazione
• Ipotesi:
• AC  CB
• D, A, B, E
allineati
• DA  BE
Enunciato
• Sui prolungamenti della base AB di un triangolo
isoscele ABC si considerino i due segmenti
congruenti AD e BE.
• Dimostrare che il triangolo DEC è isoscele.
C
• Tesi:
• DEC isoscele
Dimostrazione
D
A
B
E
Costruiamo sui prolungamenti della base AB i segmenti
congruenti DA e BE
• Ipotesi:
• AC  CB
• D, A, B, E
allineati
• DA  BE
Enunciato
• Sui prolungamenti della base AB di un triangolo
isoscele ABC si considerino i due segmenti
congruenti AD e BE.
• Dimostrare che il triangolo DEC è isoscele.
C
• Tesi:
• DEC isoscele
Dimostrazione
D
A
B
E
Uniamo D con C e E con C. Dopodichè consideriamo i
triangoli ACD e BCE. Essi hanno:
• Ipotesi:
• AC  CB
• D, A, B, E
allineati
• DA  BE
Enunciato
• Sui prolungamenti della base AB di un triangolo
isoscele ABC si considerino i due segmenti
congruenti AD e BE.
• Dimostrare che il triangolo DEC è isoscele.
C
• Tesi:
• DEC isoscele
Dimostrazione
D
AC
A
BC per ipotesi
B
E
• Ipotesi:
• AC  CB
• D, A, B, E
allineati
• DA  BE
Enunciato
• Sui prolungamenti della base AB di un triangolo
isoscele ABC si considerino i due segmenti
congruenti AD e BE.
• Dimostrare che il triangolo DEC è isoscele.
C
• Tesi:
• DEC isoscele
Dimostrazione
D
AD
A
BE per ipotesi
B
E
Enunciato
• Ipotesi:
• AC  CB
• D, A, B, E
allineati
• DA  BE
• Sui prolungamenti della base AB di un triangolo
isoscele ABC si considerino i due segmenti
congruenti AD e BE.
• Dimostrare che il triangolo DEC è isoscele.
C
• Tesi:
• DEC isoscele
Dimostrazione
D
CAD
A
B
E
CBE perché angoli supplementari ad angoli
congruenti sono congruenti fra loro
• Ipotesi:
• AC  CB
• D, A, B, E
allineati
• DA  BE
Enunciato
• Sui prolungamenti della base AB di un triangolo
isoscele ABC si considerino i due segmenti
congruenti AD e BE.
• Dimostrare che il triangolo DEC è isoscele.
C
• Tesi:
• DEC isoscele
Dimostrazione
D
A
B
E
ADC
CBE per il 1° criterio di congruenza. CD  CE
perché lati corrispondenti in triangoli congruenti.
• Ipotesi:
• AC  CB
• D, A, B, E
allineati
• DA  BE
Enunciato
• Sui prolungamenti della base AB di un triangolo
isoscele ABC si considerino i due segmenti
congruenti AD e BE.
• Dimostrare che il triangolo DEC è isoscele.
C
• Tesi:
• DEC isoscele
Dimostrazione
D
A
B
E
Il triangolo CDE è quindi isoscele sulla base DE.
c.v.d.