Calcolo delle probabilità
Progetto lauree scientifiche
Università dell’Insubria
Facoltà di Matematica
Como
Natalina Drappo
Paola Bertoncello
Introduzione
alla probabilità
Analisi degli esiti di
esperimenti aleatori
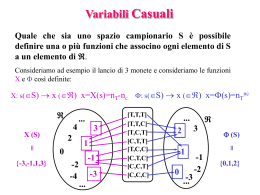
Variabile aleatoria
Grandezza i cui valori
siano i possibili esiti
di un esperimento
definizioni
Probabilità discreta
in cui l’insieme dei valori assumibili
dai risultati sia finito o numerabile
Evento elementare
Esito di un esperimento aleatorio
testa testa TT
Spazio campionario
Insieme degli eventi elementari
{TT, TC, CT, CC }
Evento
Risultato del lancio
di due monete
Sottoinsieme dello spazio
Mano di poker
campionario
{TT, TC, CT}
Probabilità classica
_____________
favorevoli
P(E)= Casi
Casi possibili
Proprietà
di un evento E
E = esce almeno una testa IEI = 3
Ω = spazio campionario
IΩI=4
del lancio di due
P(E) = ¾
monete
0≤P(E) ≤1
P(Ec)=1-P(E)
Ec= non esce alcuna
testa
IEcI = 1 P(Ec) = 1/4
E ‫ כֿ‬F → P(E) > P(F)
Ω
E
CC
F TC
TT
CT
F= esce una testa = {TC, CT}
IFI=2
P(F)=1/2
Strumenti matematici
per lo studio della probabilità
Disposizione semplice
Selezione ordinata di k elementi di un insieme finito di
dimensione n
Elenco degli studenti seduti nella prima fila
Primi tre classificati di una gara
Problema: quante disposizioni si
presentano nell’estrazione di due
palline da un sacchetto che ne
contiene 4 diverse?
Soluzione: 4 possibilità per la prima pallina
per ogni scelta della prima ci sono 3 possibilità per la seconda
per ogni scelta delle precedenti ci sono 2 possibilità per la terza
Numero di disposizioni semplici: 4 ·3 · 2 = 24
Altri esempi e relative soluzioni:
• Il numero di modi in cui disporre 4 alunni in prima fila in
una classe di 25 studenti è 25 · 24 · 23 · 22 = 303600
• le possibili disposizioni dei numeri della prima cinquina
della tombola sono
90 · 89 · 88 ·87 · 86 > 5 1010
Regola:
Il numero di k-disposizioni semplici di n elementi è
n · (n-1) ·… · (n-k+1)
Usando il fattoriale di n, definito come
n!=n · (n-1) · (n-2) · ….. · 1
ottengo:
n!
_____
D k,n =
(n-k)!
Disposizione con ripetizione
Elenco di k elementi ordinati di un insieme di dimensione n
per cui è prevista la ripetizione
Pin del telefono
Lancio di tre dadi
Problema: quanti prefissi
telefonici si possono
scrivere con tre cifre?
Soluzione:
9 possibilità per la prima cifra
Per ogni scelta della prima cifra ho 9 possibilità per la seconda
Per ogni scelta delle prime due cifre ho 9 possibilità per la terza
Disposizioni con ripetizione: 9 · 9 · 9 = 93
Altri esempi e relative soluzioni:
• Il numero di colonne possibili del totocalcio è 313 = 1594323
• il numero di password di 8 cifre che si possono scrivere
con cifre alfanumeriche maiuscole e minuscole senza
caratteri speciali è (10+26x2)8
Regola:
Il numero di k-disposizioni con ripetizione di n
elementi è
D k,n = nk
… nota
• il numero di targhe che si può ottenere con 4 numeri e 2
cifre finali è
104 · 262 = 6760000
Permutazione (semplice)
Possibile ordinamento di un insieme finito di elementi
È una n-disposizione semplice di n elementi
Ordine di arrivo ad una gara
Posizione dei libri in una libreria
Problema: in quanti modi posso distribuire i
25 studenti di una classe?
Soluzione: partendo dal primo banco, per il quale ho
25 possibilità, ad ogni scelta successiva ho uno
studente in meno a disposizione, per cui ho
25 · 24 · 23 · …..2 · 1 = 25!
Regola
Le permutazioni di n elementi sono Pn = n!
Combinazioni
Raggruppamenti di k elementi di un insieme di
dimensione n
= possibili sottoinsiemi
Studenti interrogati
Estrazioni del lotto
Problema: quante scelte ha un
professore se interroga 4 persone
in una classe di 25?
Soluzione:
Il numero di 4-disposizioni di 25 elementi è 25!/21!
Le disposizioni con gli stessi elementi in cui cambia solo
l’ordine corrispondono alla stessa composizione
Il loro numero corrisponde al
numero di permutazioni: sono 4!
Le combinazioni
sono ____
25!
21!4!
Altri esempi e relative soluzioni:
• Il numero di combinazioni vincenti del SuperEnalotto è
90!
______
84!6!
Regola:
Il numero di sottoinsiemi di k elementi di un
______
insieme di dimensione n è C
n!
=
k,n
(n-k)!k!
Definisco coefficiente binomiale
n!
il valore
n ______
k = (n-k)!k!
()
Probabilità composta
definizioni
Dico due variabili o due eventi indipendenti se il verificarsi
del primo non influenza il verificarsi del secondo.
A, B eventi indipendenti  P(A ∩ B) = P(A) · P(B)
A ={TT, TC} B = {TC, CC}
X, Y variabili indipendenti
A
Ωx
J
∩
I
∩
A

Ωy si ha
TT
TC CC CT
P(I ∩ J) = P(I) · P(J)
Ossia se tutti i possibili eventi della prima sono
indipendenti dai possibili eventi della seconda
X = esito lancio del primo dado
Y = esito lancio del secondo dado
Regole
Dati due eventi E e F
CCT
∩
P(E F) = P(E) + P(F) - P(E∩F)
E CTT TTC
TCT
E = esattamente due teste
F = la prima è testa
CTC
F
CCC
con E ∩ F = Φ ho
∩
TTT
TCC
TTC
F
E
CTC TCT
CCT
CTT
Ω
CCC
Ω
TCC
TTT
P(E F) = P(E) + P(F)
E = esattamente due teste
F = esattamente una testa
Nota: nel caso di tre eventi
∩ ∩
P(E F
G) = P(E) + P(F) + P(G) - P(E∩F) - P(E∩G) - P(F∩G) +
+ P(E∩F∩G)
Si consideri un evento costituito da eventi elementari
che siano fasi successive di un esperimento
Diagramma ad albero
struttura di oggetti (foglie) e collegamenti (rami) orientati
Ogni foglia può discendere da un solo predecessore
(padre)
Ad ogni foglia possono seguire diversi oggetti (figli)
Lancio di tre dadi
T
V
V
T
C
V V
T C T C
T
C
V V
I possibili esiti si
trovano percorrendo
tutti i rami dalla radice
alla cima
C
T CT C
Principio di moltiplicazione
Sia E l’evento che si ottiene percorrendo un ramo
dell’albero dalla radice alla cima ed ei gli eventi
elementari corrispondenti alle foglie del percorso di E
P(E) = p P(ei)
Probabilità di un
codice alfanumerico
del tipo aabc con
a:±1 b:cifra c:lettera
1
1
P(-1,1,9,y)=
½ · ½ · 1/10 · 1/26
1
__
=
1040
-1 ½
-1 -1
1 ½
0123…
a b
9
…
1/10
w y z 1/26
Probabilità condizionata
e inversa
P(F|E) = Probabilità che l’evento F si realizzi nell’ipotesi
che l’evento E si sia già realizzato
E = il primo esito è testa
P(F)=3/8
P(F|E)=2/4
CCT
F
Ω
TCC
CTT TTC
TTT
TCT
CTC
F = due esiti su tre sono testa
CCC
E
F
TTC
TCT
TCC
TTT
E = Ω
Regola
P(F∩E)
_______
P(F|E)=
P(E)
Riferendosi all’esercizio precedente
P(F∩E)=2
P(E)= 4
P(F|E)= 2/4
Nota:
F è indipendente da E se (def.) P(F|E) = P(F)
e se sostituisco trovo P(E) · P(F) = P(E∩F)
Problema della probabilità inversa
Problema:
L’urna I contiene 3 palline rosse e 2 blu, l’urna II contiene 1
pallina rossa e 1 blu. Pesco ad occhi chiusi una pallina rossa:
Quale è la probabilità che provenga dall’urna 1?
Soluzione
Uso il diagramma ad albero:
r 3/5
I
½
II
b2/5
r
½
½
b
P(e1)
P(e2)
Evento elem.
½
3/10
P(b)=9/20
1/5
1/4
P(r)=11/20
1/4
P(Ei)
i=1…4
Costruisco il diagramma inverso:
x = 4/9
I
1/5
P(I|b) = 4/9
II
1/4
P(II|b) = 5/9
6/11
I
3/10
P(I|r) = 6/11
5/11
II
1/4
P(II|r) = 5/11
9/20
b
5/9
11/20
r
Come trovare x : la probabilità dei rami equivalenti dei due
alberi è uguale, quindi:
9/20 · x = P(E2) = 1/5
P(b)
P(I|b)
P(b∩I)
Il problema corrisponde alla ricerca della probabilità
dell’urna I condizionata all’aver pescato b
Formula di Bayes
Problema:
Si consideri un esperimento in due fasi e si voglia
calcolare la probabilità di un evento elementare Hi al
primo stadio nota la probabilità dell’evento E al secondo
stadio
Regola
P(E|Hi) · P(Hi)
P(E|Hi) · P(Hi)
________________
P(Hi|E) =
= __________
 P(E|Hk) · P(Hk)
Σ
P(E)
m
k 1
Probabilità discreta
e continua
definizioni
Dato uno spazio campionario discreto Ω
*
def. probabilità su Ω una qualsiasi funzione
P:Ω
[0,1]
che soddisfi
1) P(Ω) = 1

2) P(U Ak) =
k 1


P(Ak)
k 1
* Finito o numerabile
Probabilità classica
Ω finito o numerabile con Ω = { wi }
IΩI = dimensione (o la cardinalità) di Ω
IEI
P(E) = ___
IΩI
‫ כּ‬A
E
Ω
definizione equivalente alla probabilità classica:
Sia m(x) una funzione
m:Ω
[0,1]
con
detta funzione di distribuzione di Ω
Sia E un sottoinsieme di Ω
definisco
P(E) :=

m(x)
xE
P:Ω
[0,1]
con
P(Ω) = 1
 m(x) =1
x
Le proprietà sono quelle già viste
.
le trasmettiamo dagli insiemi agli elementi
per il caso numerabile le somme diventano serie
studio della convergenza
(esistenza di una somma finita)
Caso continuo
X = lunghezza della corda di una circonferenza unitaria
Ω = ( 0,2]
Si voglia P(E)
con E = ( 3 ,2]
Scelgo un sistema di coordinate per il punto medio:
rettangolari del con origine nel centro della circonferenza
M: (x,y)
(x,y) [-1,1] x [-1,1]
con x2 +y2 ≤ 1
L’Hp corrisponde a X ≥ lato del triangolo
equilatero .
M è interno alla circonferenza di raggio ½
Nota:
Se ho uno spazio campionario sottoinsieme di IR2
e ipotizzo che tutti i suoi punti siano equiprobabili
posso associare ad una superficie una probabilità
equivalente alla sua area
P(E) =
2
π(½)
______
π(1)2
=1/4
Paradosso di Bertrand:
1/4
P(E) =
1/2
M:(x;y)
M:(ρ;θ)
1/3 A:(1;α) B:(1;β)
Nota: Area e integrale
definizione
F(x) funzione di distribuzione cumulativa di X se
FX ( x) : P( X  x) : P((, x))
FX ( x) : IR  IR 
Proprietà
FX (x) è monotona non decrescente
lim
lim
FX ( x)  0
FX ( x)  1
x  
x
FX (x) è continua da destra:
lim
FX ( x)  FX (t )

xt
definizione
f(x) funzione di densità di X se
f: IR
+
IR e vale
b

P(a ≤ x ≤ b) = f ( x)dx
a, b  IR
a
Proprietà
Scelta la variabile X non è detto che esista f(x)

P(X E) = f ( x)dx purché l’integrale esista
E
f(x) non è una probabilità.
Teorema
Sia X una variabile aleatoria con funzione di densità f(x)
x
F ( x) 

f (t )dt

Rappresenta la funzione
di distribuzione cumulativa di X,
d
F ( x)  f ( x)
dx
e si ha
Da ciò potremmo introdurre un diversa
definizione di funzione densità:

x


f: IR
f (t )dt  F ( x)
IR+
t.c.
 f ( x)dx  1

Esempi significativi di distribuzioni e densità
Distribuzione uniforme
discreta
Sia X una variabile aleatoria con spazio campionario Ω
di dimensione n
La distribuzione è rappresentata dalla funzione
m(x) = 1/n = costante
Attenzione!
Sia Ω numerabile e m(x) = costante
 m( x)dx
diverge
E 
Distribuzione uniforme
continua
Funzione di densità gaussiana
( x )2
1
fx = ______
2p
e
2 2
 0
 2 1
FINE