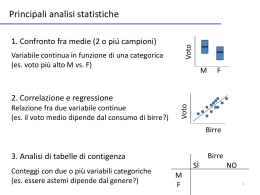
Analisi dell’output
di una simulazione
Dati di output
n repliche indipendenti di lunghezza m
1 replica  Y11 , Y12 , Y13 ,  , Y1m
a
2 replica  Y21 , Y22 , Y23 ,  , Y2 m
a






n replica  Yn1 , Yn 2 , Yn 3 ,  , Ynm
a
Transitorio e stato stazionario
Processo stocastico di output
{ Yi , i  1, 2,  }
• Distribuzione transitoria
Fi ( y | I )  P (Yi  y | I )
• Distribuzione stazionaria
lim
i
Fi ( y | I )  F ( y )
Tipi di simulazioni
Simulazioni con terminazione
analisi del transitorio
Simulazioni senza terminazione
analisi dello stato stazionario
Analisi del transitorio
X variabile aleatoria
X i realizzazi one nell' i  esima replica
X n stimatore corretto di   E ( X )
2
n
s stimatore corretto della varianza
2
n
s
 (n, )  t n 1,1 / 2
n
semiampiez za dell' I.C. 100(1   )%
Esempio (banca)
repl. clienti
ore t medio attesa
1
2
3
4
5
6
7
8
9
10
484
475
484
483
455
461
451
486
502
475
8.12
8.14
8.19
8.03
8.03
8.32
8.09
8.19
8.15
8.24
1.53
1.66
1.24
2.34
2.00
1.69
2.69
2.86
1.70
2.60
Errore assoluto
P(| X n   |  )  1  
*
na  min{ n  2 |  ( n,  )   }
Errore relativo
P(| X n   | / |  |)   )  1  

*
nr  min{ n  10 |  (n,  ) / | X n |
}
1 
Procedure
• Procedura a due fasi
• Procedura iterativa
Procedura a due fasi
prima fase : n0 repliche e calcolo di sn20 e  (n0 ,  )
2
n
seconda fase : eventuali altre repliche (senza calcolare s )
fino alla precisione desiderata
n  min{ i  n0 | ti 1,1 / 2
*
a
n  min{ i  n0 |
*
r
ti 1,1 / 2
| X n0 |
2
n0
s
i
sn20
i 
 }

1 
}
Procedura iterativa
Passo 0 : si effettuano n0 repliche e si pone n  n0
Passo 1 : si calcolano X n e  (n,  )
 ( n,  )

Passo 3 : se

si usa X n come
1 
|Xn |
stima di μ e Stop
altrimenti si effettua un' ulteriore replica,
si pone n  n  1 e si va al Passo 1
Analisi dello stato stazionario
Processo stocastico di output di una
simulazione senza terminazione
Si vuole stimare
{ Y j , j  1, 2, }
  lim j  E (Y j )  E (Y )
m
Date m osservazioni si calcola
Ym
Ym 
non è uno stimatore corretto di
Y
j 1
m

j
Problema del transitorio iniziale (“startup”)
Esempio: sistema di code M/M/1 con
  1 e   10 9
T  lim E (t )
q
i 
q
i
Analiticamente si calcola
T  8.1
q
grafico di E (tiq ) al variare di i
per diversi valori del numero di utenti nel sistema al tempo 0
Cancellazione dei dati iniziali (“warming up”)
m
Y ( m ,l ) 
Y
j l 1
j
ml
Determinar e l tale che per i  l risulti
E (Yi )  
Procedura di Welch
Passo 1: si effettuano n repliche di lunghezza m
Y11, Y12 , Y13 ,, Y1m
Y21, Y22 , Y23 ,, Y2 m




Yn1 , Yn 2 , Yn 3 ,, Ynm
Passo 2: si costruisce la successione
Y 1 , Y 2,
 ,
Ym
n
Yj
Y
i 1
n
ij
Passo 3: dato k  m / 4
successione
si sostituisce ciascun termine della
Y 1 , Y 2,
 ,
Ym
con
k
Y j (k ) 
Y
j h
h  k
2k  1
per j  k  1,  , m  k
j 1
Y j (k ) 
Y
jh
h   ( j 1)
2 j 1
per j  1,  , k
Passo 4: si sceglie quel valore di l oltre il quale la successione
Y
j

(k )
appare giunta a convergenza