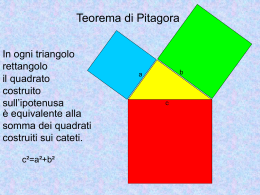
Questo ipertesto è stato realizzato da:
dr. Rita Agnelli
dr. Elisabetta Porrera
dr. Sofia Sabatti
dr. Chiara Zaina
Il suo utilizzo è consentito
esclusivamente previa autorizzazione
da parte delle autrici.
E-mail: [email protected]
IL TEOREMA DI PITAGORA
Francobollo emesso dalla Grecia il 20 agosto 1955.
LA SFIDA
CASI PARTICOLARI
EUCLIDE
IL TEOREMA
DI PITAGORA
DIMOSTRAZIONI
LEGAMI CON ALTRE
DISCIPLINE
LA STORIA
GLI IRRAZIONALI
INDICE
1. LA SFIDA
•
•
•
•
il problema della duplicazione del quadrato
errori comuni
soluzione del problema
un esercizio
2. CASI PARTICOLARI
• un triangolo rettangolo isoscele
• terne pitagoriche
• una verifica numerica
3. IL TEOREMA DI PITAGORA NEGLI
ELEMENTI DI EUCLIDE
•
•
•
•
un nuovo personaggio: Euclide
la sua opera: gli Elementi
libro I, prop. 47 - 48
libro VI, prop. 31
4. DIMOSTRAZIONI
• cosa significa dimostrare
• alcune dimostrazioni significative
5. LA STORIA
• le civiltà potamiche
- Egiziani
- Babilonesi
- Indiani
- Cinesi
• Pitagora e la sua scuola
6. UN’INTRODUZIONE AI NUMERI
IRRAZIONALI
• la duplicazione del quadrato e la radice quadrata
di 2
• costruzione della radice quadrata di n
• aspetti naturalistici
7. LEGAMI CON ALTRE DISCIPLINE
• educazione artistica
- origami
- la spirale della Sagrada Familia
• educazione tecnica
“pesiamo” il teorema di Pitagora
8. BIBLIOGRAFIA ED ELENCO SITI
CIAO, SONO PIT!
Ti accompagnerò alla scoperta del
“Teorema di Pitagora”.
Un teorema è un enunciato la cui validità è
assicurata da una dimostrazione rigorosa.
Quello di cui ci occuperemo riguarda la
geometria e deve il suo nome ad un personaggio
che conosceremo insieme: Pitagora.
Durante l’esplorazione di questo mondo
affascinante, fai attenzione ai miei consigli: ti
aiuteranno a scoprire i segreti nascosti di tante
figure, a capire meglio quello che ti verrà
spiegato e a risolvere i problemi che incontrerai!
1. LA SFIDA
La chiave di
accesso alla nostra
avventura insieme
è la tua voglia di
metterti in gioco:
benvenuto, allora,
alla nostra prima
sfida!
La sfida che ti propongo è questa:
sai disegnare un quadrato che abbia
area doppia rispetto a quella di
un quadrato assegnato?
Disegna un quadrato sul tuo quaderno e poi
disegnane uno di area doppia.
Se ti sembra un problema inutile...
… prova a pensare di essere un sarto e di aver
cucito un fazzoletto che, alla fine, risulta essere
troppo piccolo: cosa faresti se te ne
commissionassero uno grande il doppio?
E se tu fossi un geometra e dovessi preparare
un preventivo per la recinzione di un
appezzamento di terreno quadrato, di area
doppia rispetto all’ultimo di cui ti sei occupato?
Se ci sei già riuscito…
sei veramente incredibile!
Se invece hai bisogno di una mano,
prova a leggere
qui sotto...
Molti, al primo tentativo,
quadruplicano il quadrato, invece
di raddoppiarlo.
Altri raddoppiano l’area, ma invece
di disegnare un quadrato,
disegnano un rettangolo.
Prova a concentrarti e ad usare un
po’ della fantasia che hai...
Devo pensare,
devo provare
e riprovare…
Ma come faccio
a non abbattermi?!...



Hai provato a
suddividere il quadrato in
altre figure più piccole?
Hai pensato che se il tuo
quadrato contiene (ad
esempio) quattro figure
uguali il suo doppio ne
dovrà contenere otto?
Hai provato con figure
diverse… ad esempio
con dei triangoli?
Congratulazioni! Sono
sicuro che, a questo
punto, hai trovato la
soluzione.
Prova a confrontarla con
quella che ho trovato io…
Ti propongo ora un’altra sfida: sai disegnare
un quadrato che abbia area dimezzata rispetto
a quella di un quadrato assegnato?
Se sei stato attento, non ti sarà difficile
disegnare un quadrato sul tuo quaderno e
poi disegnane uno che abbia area la metà.
2. CASI PARTICOLARI
-
i quadrati costruiti sui lati di un
triangolo rettangolo isoscele;
-
le terne pitagoriche;
-
una verifica numerica un po’ più
generale.
Sono sicuro che sarai molto orgoglioso di aver
risolto il problema della duplicazione del quadrato.
Ora vorrei solo farti notare che si può leggere tale
soluzione anche in un altro modo:
dato un triangolo rettangolo isoscele,
il quadrato costruito sulla sua
ipotenusa
è equivalente alla somma dei due
quadrati costruiti sui due cateti.
Ebbene: secondo te, questa proprietà
(che abbiamo verificato valere per i triangoli
rettangoli isosceli) sarà valida anche per altri
triangoli rettangoli?
Prova a disegnare sul tuo
quaderno un triangolo che abbia
i lati di 3 cm, 4 cm e 5 cm.
Verifica che è rettangolo e poi
vedi se il quadrato costruito
sulla sua ipotenusa è
equivalente (o no) alla somma
dei due costruiti sui suoi cateti.
Se hai fatto i calcoli giusti, dovresti aver già
verificato che, anche in questo caso particolare, il
quadrato costruito sull’ipotenusa è equivalente alla
somma dei due costruiti sui cateti.
Prova a disegnare sul tuo quaderno un triangolo
che abbia i lati di 6 cm, 8 cm e 10 cm.
Verifica che è rettangolo e poi vedi se il quadrato
costruito sulla sua ipotenusa è equivalente (o no)
alla somma dei due costruiti sui suoi cateti.
Ed ora, per allenarti ancora
un po’, prova a verificare
cosa succede per un
triangolo che abbia i lati di
5 cm, 12 cm e 13 cm.
Ti sarai reso conto che in tutti questi casi si
ottiene un triangolo rettangolo, per il quale il
quadrato costruito sull’ipotenusa è
equivalente alla somma dei due costruiti sui
cateti.
Terne di numeri naturali di questo tipo sono
dette
terne pitagoriche.
In altre parole, tre numeri naturali a, b e c
formano una terna pitagorica se
a b  c
2
2
2
Per ora abbiamo incontrato queste terne
pitagoriche:
(3, 4, 5), (6, 8, 10), (5, 12, 13).
Ce ne sono altre?
Che ne dici?
7
24
25
Probabilmente sarai già riuscito a trovare tantissime
terne pitagoriche.
Se vuoi un consiglio,
fermati qua: tutto il tempo
della tua vita non ti
basterebbe per trovarle
tutte, perché sono
infinite…!
Infatti, comunque presi due numeri naturali x e y
si ha che i numeri
a = x2 - y2
b=2xy
c = x2 + y2
costituiscono una terna pitagorica.
Abbiamo allora visto che per infiniti triangoli
rettangoli (tutti quelli i cui lati hanno le misure
corrispondenti ai numeri di una terna pitagorica)
il quadrato costruito sull’ipotenusa è equivalente
alla somma dei due costruiti sui cateti.
Ora scopriremo, facendo qualche misura, che i
triangoli rettangoli per cui vale questa proprietà
sono… ancora di più!
Ebbene, anche se abbiamo visto che per infiniti
triangoli rettangoli il quadrato costruito
sull’ipotenusa è equivalente alla somma di quelli
costruiti sui cateti, nulla ci permette ancora di dire
che ciò avviene per tutti i triangoli rettangoli.
Sarà così o non sarà così?
Chi ce lo assicura?
È quello che vedremo insieme, se hai la pazienza
e la voglia di continuare questo viaggio con me!
3. IL TEOREMA DI
PITAGORA...
… PRESENTATO
DA EUCLIDE!
Incontriamo adesso un nuovo
personaggio, che ci illustrerà
come ha dimostrato il nostro
ormai noto teorema di Pitagora.
Avete idea di chi possa essere?
Provate a pensare, forse lo avete già
incontrato…
…vi dicono niente le parole assiomi, nozioni
comuni, Elementi…?
Adesso dovreste proprio avere capito di chi
stiamo parlando!
Si tratta di Euclide!
EUCLIDE
IV - III sec. a.C.
Euclide è l’autore del trattato di geometria
più diffuso nel mondo; ciò nonostante
sono pochissime le informazioni che
possediamo circa la sua vita.
Secondo quanto si legge nel Commentario al primo libro degli
Elementi di Proclo (V sec. d.C.), Euclide è vissuto tra il IV e il
III secolo a.C. ad Alessandria, in Egitto, e appartiene a quel
periodo che è noto come età aurea della matematica greca.
Dopo aver ricevuto la sua formazione ad Atene, presso la
scuola di Platone, viene chiamato ad Alessandria, maggior
centro culturale dell’antichità, per insegnare matematica.
Di questo periodo, si narrano due aneddoti che ci
forniscono qualche notizia sul temperamento di questo
personaggio.
Alla richiesta del sovrano Tolomeo di fornirgli una facile
introduzione alla geometria, Euclide risponde che non
esistono vie regie che portano a tale disciplina.
In un’altra occasione, ad una alunno che chiede quali
vantaggi si possono trarre dallo studio della geometria,
Euclide fa dare, da un suo servo, una moneta per
sottolineare che l’allievo ha bisogno di trarre un vantaggio
pratico da ciò che impara e poi lo caccia via.
Ad Alessandria Euclide scrive gli Elementi, che
diventeranno l’opera matematica più nota e
conosciuta, tanto da essere il testo più tradotto dopo
la Bibbia.
Si tratta di un manuale introduttivo allo studio della
matematica, costituito da 13 libri che trattano
rispettivamente di:
• libri I - VI: geometria piana;
• libri VII - IX: teoria dei numeri;
• libro X: le grandezze
incommensurabili;
• libri XI - XIII: geometria solida.
Il Teorema di Pitagora viene enunciato e dimostrato
nella proposizione 47 alla fine del libro I.
A testimonianza delle
numerosissime
traduzioni degli Elementi
in svariate lingue, voglio
mostrarti questa
immagine che illustra la
prima proposizione del
primo libro degli
Elementi di Euclide,
tradotti in cinese nei
primi anni del XVII
secolo dal gesuita
Matteo Ricci.
Un’altra edizione molto
interessante degli
Elementi è questa
versione in lingua
inglese a colori, dovuta a
Oliver Byrne, che risale
al 1847.
Ti mostro ora le
proposizioni degli
Elementi che riguardano
il teorema di Pitagora.
Le cito dalla edizione in
italiano dell’UTET curata
da Attilio Frajese e
Lamberto Maccioni.
Libro I, proposizione 47
Nei triangoli rettangoli il quadrato del
lato opposto all’angolo retto è uguale
alla somma dei quadrati dei lati che
comprendono l’angolo retto.
Con la proposizione 48 del libro I, Euclide
risponde a questo problema:
dato un triangolo e costruiti i quadrati sui suoi
lati, se la somma di due dei quadrati è uguale al
terzo, possiamo affermare con certezza che il
triangolo è rettangolo?
?
Libro I, proposizione 48
Se in un triangolo il quadrato di uno dei
lati è uguale alla somma dei quadrati
dei rimanenti due lati del triangolo,
l’angolo che è compreso dai due
rimanenti lati del triangolo è retto.
Con la proposizione 31 del libro VI, Euclide
risponde a questo problema:
sui lati del triangolo rettangolo, devo costruire
proprio dei quadrati? Il teorema non vale se
costruisco altre figure?
?
Libro VI, proposizione 31
Nei triangoli rettangoli la figura descritta
sul lato opposto all’angolo retto è
uguale alla somma delle figure simili e
similmente descritte sui lati che
comprendono l’angolo retto.
Cliccando su queste immagini puoi
verificare quanto Euclide dice nella
proposizione 31 per due casi particolari.
4. IL TEOREMA DI PITAGORA?
DIMOSTRAMELO!
Fin da prima di Euclide, i matematici
non si sono accontentati di accorgersi
di alcune proprietà dei numeri e delle
figure geometriche, bensì hanno
sentito l’esigenza di dimostrarle.
Ma cosa vuol dire dimostrare?
Prova a pensare con i tuoi compagni al significato
di questo verbo.
Non si tratta di vedere chi per primo indovina la
definizione esatta, ma di provare insieme a
riflettere sui diversi modi e sulle diverse occasioni
in cui ciascuno di voi ha usato, sentito o letto
questa parola.
Datevi tempo e scrivete
su un foglio di carta le
cose che vi vengono in
mente.
Ora provate a cercare su un vocabolario della
lingua italiana i significati di questa parola e
confrontateli con quelli che avevate trovato voi.
Io, sul Vocabolario della lingua italiana di Nicola
Zingarelli edito da Zanichelli, ho trovato questi
significati:
1) mostrare o manifestare apertamente uno stato,
una qualità, un sentimento e sim., con fatti, parole,
segni esteriori;
2) provare la verità di un enunciato, di una tesi, di
una dottrina e sim. fornendo le necessarie prove;
3) spiegare, insegnare, far vedere;
4) scoprire;
5) prendere parte ad una dimostrazione pubblica.
Nessuno di questi significati è quello a cui pensano i
matematici quando parlano di dimostrazioni.
È vero però che alcune parole usate dal vocabolario
possono esserci utili per avvicinarci al significato
specifico che vogliamo dare a questo verbo.
Probabilmente alcune di queste parole chiave si
trovano anche tra le definizioni o i sinonimi che
avete dato voi:
• mostrare - manifestare - far vedere;
•provare - prove;
• scoprire;
• insegnare - spiegare;
• apertamente - con segni esteriori.
L’idea di “mostrare” è importante: ci dice che una
dimostrazione deve essere chiaramente comprensibile a chi
la fa e a chiunque la legga.
Anche quando si fa riferimento ai “segni esteriori” si intende
dare importanza al fatto che una dimostrazione deve essere
comunicabile: non può essere qualcosa che abbiamo solo in
mente o solo nel cuore.
Quando si parla di “prove” si sottolinea il fatto che una
dimostrazione deve essere convincente, non deve lasciare
spazio a dubbi o perplessità.
Infine le dimostrazioni ci rendono sicuri delle nostre
scoperte e ci permettono di insegnarle anche agli altri.
Per i matematici dimostrare significa passare da
certe premesse accettate, che chiamiamo ipotesi,
a una proposizione, che chiamiamo tesi,
attraverso una sequenza finita di ragionamenti
logici.
L’ipotesi, la tesi e la
dimostrazione costruita da un
matematico per passare dalla
prima alla seconda
costituiscono un teorema.
Vediamo ora qual è l’ipotesi e qual è la tesi del
teorema di Pitagora
(proposizione 47 del libro I di Euclide).
Successivamente vedremo tanti diversi modi di
dimostrarlo. Anzi: prima di guardare le
dimostrazioni che ti propongo io, datti da fare per
inventarne una tu!
Ipotesi: ABC è un triangolo
rettangolo, retto in A.
Tesi: il quadrato costruito
sull’ipotenusa BC è equivalente
alla somma di quelli costruiti sui
cateti AB e AC.
Abbiamo analizzato insieme la proposizione 47
evidenziando ipotesi e tesi.
Prova a fare lo stesso con la proposizione 48.
Quali analogie puoi trovare?
Prova a confrontare l’ipotesi
dell’uno con la tesi dell’altro
e viceversa...
Avrai certamente notato che l’ipotesi della
proposizione 47 corrisponde alla tesi della
48 e l’ipotesi della 48 alla tesi della 47.
Non è uno scioglilingua!
Se in questo modo ti ho confuso le idee,
chiariscitele con il seguente schema:
ABC è un triangolo rettangolo in A
47
48
Il quadrato costruito su BC è
equivalente alla somma di quelli
costruiti su AB e AC.
Proposizioni come la 47 e la 48 del I libro
degli Elementi si dice che sono l’una
l’inversa dell’altra.
Una dimostrazione…
mobile!
La dimostrazione che ti
propongo ora è una
variazione di quella
originale di Euclide, che
puoi trovare alla
proposizione 47 del
libro I degli Elementi.
Clicca su questa icona
e… vedrai!
Una dimostrazione che
sfrutta le similitudini.
La dimostrazione che puoi
vedere da qui richiede che ti
siano noti i criteri di
similitudine dei triangoli e le
loro conseguenze.
Euclide affronta questi temi
nel libro VI degli Elementi.
Una dimostrazione per
scomposizione e
movimenti rigidi.
Questa dimostrazione, per essere davvero
formale, richiede lo studio delle isometrie (o
movimenti rigidi). Anche se non li conosci a
fondo, cliccando su questa icona ne puoi capire lo
spirito!
La dimostrazione… del
presidente.
Questa dimostrazione, richiede una certa
familiarità con l’uso delle formule, ma… se vuoi ce
la puoi fare anche tu (ce l’ha fatta il Presidente
degli U.S.A!).
5. LA STORIA
Abbiamo già parlato di Euclide,
uno dei personaggi legati al
teorema di Pitagora.
Ma la storia di questo teorema è
cominciata molto tempo prima.
Se proprio insisti… te la racconto!
IL TEOREMA NELLE CIVILTA’
POTAMICHE
Quello che noi chiamiamo Teorema di
Pitagora era noto, con altri nomi,
anche ad altre civiltà?
Sembra proprio di sì…
… e adesso te lo mostrerò.
Preparati ad un viaggetto nel tempo!
Cominciamo in ordine di tempo,
ovvero con la civiltà più antica: quella degli
EGIZIANI
Devi sapere che presso questa cultura non si è
raggiunta una vera e propria conoscenza del teorema;
infatti non ci sono pervenuti documenti o testimonianze
a riguardo.
Ma le esigenze pratiche legate alla
misurazione per tracciare la pianta
dei templi o per ridefinire i confini
cancellati dalle inondazioni del
Nilo, portarono allo sviluppo di una
prima forma di geometria.
Per ottenere il triangolo rettangolo e disegnare
l’angolo retto necessario per la misurazione dei
terreni e per la squadratura dei blocchi di pietra dei
templi, i geometri egiziani ricorsero a corde divise in
12 parti uguali tramite dei nodi.
Per questo motivo i geometri egiziani sono chiamati
anche "tenditori di corde" o "agrimensori”.
Prova ad immedesimarti
in un architetto egiziano.
Come faresti ad ottenere l’angolo retto?
Confronta ora la soluzione che hai dato con quella dei
tuoi amici agrimensori.
I geometri egiziani fissavano sul terreno il quarto e
l’ottavo nodo della corda e poi la tendevano agli estremi;
in tal modo ottenevano un
triangolo rettangolo di lati 3, 4, 5.
Questi numeri formano la più famosa fra le terne
pitagoriche.
Spostiamoci ora nella regione
compresa
fra i fiumi Tigri ed Eufrate, dove vivevano i
BABILONESI
Pare che in Mesopotamia la geometria e l'algebra avessero
raggiunto un livello più elevato rispetto a quello ottenuto
dagli Egiziani.
Infatti abbiamo a disposizione documenti che attestano
una conoscenza consapevole del teorema di Pitagora:
esistono tavolette appartenenti al periodo babilonese
antico (vedi figura) che mostrano un largo utilizzo del
teorema.
E non solo! Più avanti
incontreremo un nuovo
numero: la radice
quadrata di 2.
Sappi che anche i
babilonesi la
conoscevano!
Ci sono pervenuti anche alcuni esercizi con i quali si
dilettavano i ragazzi di questo popolo; immagino che
adesso non vedrai l'ora di provare a risolvere uno di
questi problemi. Eccoti accontentato!
“Una scala o una trave di lunghezza 0,30 è
appoggiata a una parete; si chiede: di
quanto si allontanerà dalla parete
l’estremità inferiore se l’estremità
superiore scivola giù per una distanza di
0,6 unità?”
Io adesso ho bisogno
di riposare!
Tu, invece, impegnati
e risolvi questo
problema!
Una canna è
appoggiata ad una
parete. Se la cima
scivola giù di 3 unità
quando l’estremità
inferiore scivola via
di 9 unità, quanto è
lunga la canna?
…e in
INDIA ?
Alcuni scavi archeologici documentano
l’esistenza, in questa regione, di un’antica e
raffinata civiltà durante il periodo dei
costruttori delle piramidi egiziane; ma non ci è
pervenuto alcun documento matematico
indiano risalente a tale epoca.
Anche qui tuttavia le conoscenze matematiche
sono legate alla pratica (costruzione di templi,
misurazione di altari…) e, per quanto riguarda
il teorema di Pitagora, presentano decise
analogie con la matematica mesopotamica.
Troviamo infatti nel Sulvasutra di Apastamba, che
risale forse fino al tempo di Pitagora, regole per la
costruzione di angoli retti per mezzo di tre
cordicelle, le cui lunghezze formano terne
pitagoriche come 3, 4 e 5, oppure 5, 12 e 13,
oppure 8, 15 e 17, oppure 12, 35 e 37.
Queste terne si possono facilmente ricavare
dall’antica regola babilonese.
Apastamba conosceva la regola secondo cui il
quadrato costruito sulla diagonale di un rettangolo
è uguale alla somma dei quadrati costruiti sui due
lati adiacenti; tuttavia è possibile che anche questa
forma del teorema di Pitagora provenisse dalla
Mesopotamia.
Spostiamoci adesso in un'altra
parte del globo e andiamo in
CINA
Anche presso questa civiltà troviamo tracce
del teorema di Pitagora.
In un testo databile tra il 200 a.C. e il 200
d.C. intitolato Chou Pei (Classico Aritmetico
dello Gnomone e delle Orbite Circolari del
Cielo), si riscontra infatti una primitiva analisi
del triangolo rettangolo e un'acquisita
conoscenza del teorema di Pitagora.
Nel secondo libro di questo trattato è presente
il seguente dialogo tra il principe Chou Kung e il
suo ministro Shang Kao:
Una volta, Chou Kung si rivolse a Shang Kao,
dicendo: “Ho sentito che il Grande Prefetto è versato
nell’arte del calcolo. Posso avere l’ardire di chiedere
in che modo Fu- Hsi stabilì anticamente i gradi della
sfera celeste? Non vi sono scalini con cui si possa
salire al cielo e la terra non è misurabile con un
regolo della lunghezza di un piede. Mi piacerebbe
sapere da te qual è l’origine di questi numeri”.
Shang Kao rispose: “L’arte del calcolo proviene dal
cerchio e dal quadrato. Il cerchio è derivato dal
quadrato e il quadrato dal rettangolo.
Il rettangolo ha origine dal (fatto che) 99 = 81.
Dividiamo perciò un rettangolo e poniamo che la larghezza sia di 3
(unità) e la lunghezza di 4 (unità). La diagonale fra i (due) angoli sarà
allora lunga 5 (unità). Adesso, dopo aver disegnato un quadrato su
questa diagonale, circoscriviamolo con mezzi rettangoli come quello
che è rimasto fuori, in modo da formare una tavola (quadrata). I
“quattro” mezzi rettangoli esterni che misurano 3 unità di larghezza, 4
di lunghezza e 5 di diagonale, formano in tal modo insieme due
rettangoli (di superficie 24); così (quando questa viene sottratta dalla
tavola quadrata di superficie 49) il resto è una superficie di 25 unità.
Questo (procedimento) è chiamato “accumulare i rettangoli”.
I metodi usati da Yu il Grande per governare il mondo erano
derivati da questi numeri”.
Chou Kung esclamò: “Davvero grande è l’arte del calcolo. Mi
piacerebbe conoscere il Tao dell’uso del triangolo
rettangolo”.
Shang Kao rispose: “Il triangolo rettangolo in piano (posto
sul terreno) serve a stendere il progetto di (opere) diritte e
squadrate (con l’aiuto di) corde. Il triangolo rettangolo
inclinato serve ad osservare le altezze. Il triangolo
rettangolo rovesciato serve a scandagliare le profondità. Il
triangolo rettangolo in posizione orizzontale è usato per
accertare le distanze.
Mediante la rotazione di un triangolo rettangolo (compasso) si
può formare un cerchio. Unendo triangoli rettangoli si formano
quadrati (e rettangoli).
Il quadrato appartiene alla terra, il cerchio appartiene al cielo,
in quanto il cielo è rotondo e la terra è quadrata. Poiché i
numeri del quadrato costituiscono il modello, le (dimensioni
del) cerchio vengono (dedotte) da quelle del quadrato.
Il cielo è come un cappello da sole conico. I colori del cielo
sono il blu e il nero, quelli della terra il giallo e il rosso. Per
rappresentare il cielo viene usata una tavola circolare,
tracciata secondo i numeri celesti; sopra, come un indumento
esterno, essa è blu e nera, sotto, come un indumento interno,
è rossa e gialla. Così viene rappresentata la figura del cielo e
della terra.
Colui che comprende la terra è un uomo saggio, e colui che
comprende il cielo è un sapiente. La conoscenza è derivata
dalla linea retta. La linea retta è derivata dall’angolo retto. E
la combinazione dell’angolo retto con i numeri è il principio
che guida e governa le diecimila cose”.
Chou Kung esclamò: “Davvero eccellente!”
Il testo ora riportato è completato
diagramma, chiamato Hsuan Thu.
dal
seguente
Il commentatore Liu Hui definisce tale
diagramma come “il diagramma che
fornisce i rapporti fra l’ipotenusa e la
somma e la differenza degli altri due lati
per cui si può ricavare ciò che è ignoto da
ciò che è noto.”
Osserviamo che la formula algebrica che
nel testo è espressa a parole corrisponde
alla seguente:
ab
h  a  b   4
 a 2  b2
2
2
2
avendo indicato con la lettera h l’ipotenusa , con la lettera a
l’altezza e con la lettera b la base del triangolo rettangolo.
PITAGORA E LA SUA SCUOLA
Ora ti condurrò alla scoperta di Pitagora,
questo illustre sconosciuto, e della sua scuola,
ma...
… mi serve la tua attenzione!
Pitagora, scienziato e filosofo
greco, nacque nell’isola di
Samo nel VI secolo a.C..
Le notizie riguardanti la sua
vita sono spesso avvolte da
un alone leggendario.
I suoi viaggi in Egitto e in
India gli permisero di entrare
in contatto con concezioni
mistiche e matematiche
nuove ed interessanti, che lo
portarono poi a fondare a
Crotone una comunità: la
“scuola pitagorica”.
Il mistero che avvolgeva sia
Pitagora che i suoi seguaci
insospettiva e intimoriva gli
abitanti di Crotone che
scacciarono i pitagorici e
costrinsero Pitagora a
rifugiarsi nel Metaponto
(l’attuale Basilicata), dove poi
morì verso la fine del V secolo
a.C.
Pitagora rappresentato in un
particolare della Scuola di Atene
di Raffaello
Ora ti racconto un aneddoto
sulla vita di questo nostro
nuovo amico.
Si dice che mentre Leone,
principe di Flio, assisteva ai
Giochi Olimpici, chiese a
Pitagora come si sarebbe
definito. Pitagora rispose: “Io
sono un filosofo”, ma Leone
non aveva mai sentito prima
quella parola e chiese
spiegazioni. Pitagora allora
rispose, più o meno, così...
“La vita, principe Leone, può essere ben a ragione
paragonata a questi giochi olimpici, perché nella vasta folla
qui convenuta taluni sono attirati dal guadagno, altri sono
mossi solo dalla speranza e dall’ambizione di ottenere la
fama e la gloria. Ma tra costoro ve ne sono alcuni, che sono
venuti qui per osservare e capire che cosa accade.
Nella vita avviene lo stesso. Alcuni sono influenzati
dall’amore della ricchezza, mentre altri sono ciecamente
condotti dal folle desiderio di potere e di dominio, ma
l’uomo migliore si dedica a scoprire il significato e lo scopo
della vita stessa. Egli cerca di scoprire i segreti della natura.
È questo l’uomo che io chiamo filosofo perché, sebbene
nessun uomo sia completamente saggio sotto ogni rispetto,
egli può amare la sapienza in quanto chiave di accesso ai
segreti della natura.”
(Singley, L’ultimo teorema di Fermat, Sansoni)
Ora, occupiamoci un po’ della
scuola pitagorica. Non devi
immaginarti una scuola come
quella che frequenti tu oggi;
essa aveva piuttosto le
caratteristiche di una setta
religiosa; in essa si viveva una
rigida vita morale ed ascetica,
nella quale si coltivavano le
diverse componenti della
matematica.
L’appartenenza effettiva alla scuola, che
durava per tutta la vita, era concessa ai soli
uomini: le donne potevano unicamente
ascoltare le lezioni. I membri erano vincolati
al segreto, relativamente alle conoscenze
che nella scuola venivano apprese e
coltivate. Per quanto concerne la sfera
filosofica i pitagorici si ispiravano alla
religione greca: ritenevano fondamentale
purificare l’anima dalla contaminazione del
corpo.
Novità ed elemento
caratterizzante di questa
concezione filosofica era la
scienza vista dunque
come strumento di
purificazione.
Dopo la morte di Pitagora
i suoi seguaci si
dispersero, diffondendo
ovunque i risultati dei loro
studi.
Studi dei
Pitagorici
Gli allievi della scuola di Pitagora
studiavano geometria, musica,
astronomia e matematica.
Non usavano libri; ogni scoperta
veniva messa in comune,
divenendo patrimonio di tutti.
I Pitagorici conoscevano i numeri
interi e razionali e li
rappresentavano con sassolini
disposti in vario modo. Proprio tale
rappresentazione dei numeri
rendeva facile il passare
dall’aritmetica alla geometria:
l’uno era il punto, il due la linea, il tre la superficie e il quattro
il solido, il dieci (considerato il numero perfetto) era un
triangolo equilatero nel quale per ogni lato si ripete il numero
quattro.
Tra i contributi, in ambito matematico, che
vengono attribuiti ai pitagorici ricordiamo:
• il teorema relativo alla somma degli angoli
interni di un triangolo;
• il teorema di Pitagora;
• lo studio dei poliedri regolari;
• l’incommensurabilità del lato e della diagonale
del quadrato.
Pitagora e il “suo” teorema
Perché il teorema di Pitagora porta
il nome di questo personaggio così
misterioso?
…non essere impaziente, continua questo
viaggio con me!
“Allorché Pitagora trovò il famosissimo teorema,
di buoi un grandioso sacrificio celebrò”
Apollodoro di Atene (II sec d.C.)
Secondo Diogene Laerzio, storico del III sec d.C., fu
Pitagora stesso ad enunciare il teorema che porta il suo
nome; Proclo (410-485 d.C.), noto commentatore degli
Elementi di Euclide e fonte storica di rilievo non
trascurabile, conferma la tradizione letteraria (della
quale troviamo traccia anche in Cicerone) secondo la
quale Pitagora avrebbe sacrificato buoi agli dei per
festeggiare il grande traguardo raggiunto con la
scoperta del teorema.
Anche se, come abbiamo
visto, la tradizione
attribuisce a Pitagora la
paternità di questo
teorema, è difficile
distinguere l’opera del
maestro da quella dei suoi
seguaci. Tanto più che le
attribuzioni a Pitagora
risalgono ad un’epoca
successiva a quella in cui
egli visse.
6. I NUMERI… NUOVI!
3
5
2
7
n
Ma che numero è?
All’inizio della nostra avventura insieme ti
avevo lanciato una sfida: costruire un
quadrato di area doppia ad uno dato. Ora
possiamo chiederci: se assumiamo il lato
del quadrato di partenza come unità di
misura, quanto misura il lato del quadrato
di area doppia? Cioè: quante volte ci sta il
lato del primo quadrato in quello del
secondo?
La risposta a questa domanda è data da
un numero… “nuovo”.
Prova a pensare.
Se il lato del primo quadrato misura 1,
la sua area avrà valore
1x1=1
Ma allora, il quadrato di area doppia a
questa
deve avere area 2 (cioè il doppio di 1).
Quindi il suo lato dovrà avere per misura
un numero n tale che
nxn=2
Qual è questo numero?
Hai le idee un po’ annebbiate?
Non preoccuparti, anche a me succede qualche
volta.
E sta pur tranquillo che non è così solo per noi:
anche gli antichi Greci, quando si resero conto
che i numeri che avevano sino ad allora
“inventato” (o “scoperto”?)
non bastavano per misurare le lunghezze di tutti i
segmenti, si sentirono parecchio confusi.
I Greci non diedero un nome a questo numero;
forse perché non accettavano che potesse
esistere,
anche se ce l’avevano lì, davanti agli occhi.
Be’, facciamo presto a dirlo noi,
più di 2000 anni dopo!
Ad ogni modo, noi abbiamo sia un nome sia un
simbolo per questo numero.
Si chiama radice quadrata di due
e si indica così:
2
2
Un altro modo per
indicare il nostro
nuovo amico...
In inglese “radice quadrata” si dice
“square root”.
Da questa parola deriva
un altro modo per indicare
la radice quadrata di 2:
sqrt (2).
A questo punto, credo che possiamo porci
due domande:
• cosa ha a che fare questo nuovo
numero con il teorema di Pitagora?
• la radice di due è l’unico numero nuovo
che questo teorema ci “costringe” ad
inventare?
3
E va bene.
Abbiamo conosciuto due nuovi numeri.
Ma ce ne sono altri, che possiamo
scoprire grazie al teorema di Pitagora?
Direi proprio di sì.
Anzi, è importante anche che ci rendiamo
conto che la natura aveva scoperto
questi numeri molto tempo prima di noi…
e prima di Pitagora!
Se apri questo file vedrai come, disegnando
successivi triangoli rettangoli sino a formare una
specie di spirale, si riescono a costruire segmenti
la cui misura è
2,
3,
4,
5,
6,
7 ,...
Questa è invece l’immagine di un fossile di
ammonite: la sua forma non ti ricorda forse
quella della spirale che abbiamo appena
costruito?
Questa è un’immagine che illustra la galassia a spirale
ordinaria NGC 628 M74
Non ti ricorda forse la nostra spirale?
7. LEGAMI ALTRE DISCIPLINE

Educazione artistica:
– gli origami
– la spirale della Sagrada Familia

Educazione tecnica: metodo
archimedeo della bilancia
Educazione Artistica
Spesso hai giocato con fogli
di carta piegati in vario
modo, hai costruito barche,
rane che saltellano… Questo
non è solo un gioco, ma è
anche una forma d’arte: gli
origami.
Ora ti farò una richiesta
insolita:prova a dimostrare il
teorema di Pitagora con gli
origami.
Non abbatterti… ti darò un piccolo aiuto: prendi
un foglio quadrato e suddividilo in nove
quadrati equiestesi.
Piega un foglio di carta quadrato come
in figura:
Osserva il triangolo FAB: è un
triangolo rettangolo con ipotenusa
AB e cateti FB e FA.
Piega il foglio lungo le linee AO e
NO: otterrai il quadrato costruito sul
cateto maggiore (AONF); ora
piegando il quadrato così ottenuto
lungo la linea BK, otterrai la
seguente figura che è costituita
dalla somma dei due triangoli dati.
Ne segue che il quadrato FNOA
equivale a 4 triangoli FAB.
Piegando il foglio lungo i lati BA, BC, CD, DA
si potrà osservare che il quadrato centrale
vuoto non è altro che il quadrato costruito sul
cateto minore e il quadrato globale è il
quadrato costruito sull'ipotenusa.
Abbiamo già detto che il teorema di Pitagora ci
permette di costruire una caratteristica spirale;
tale figura ricorre anche nell’arte. Osserva
l’effetto ottico prodotto da questa scala a
chiocciola. Si trova in una delle torri della
Sagrada Familia, chiesa progettata da A. Gaudì
e in costruzione a Barcellona (Spagna).
Educazione Tecnica
Ora ti farò un’altra richiesta
inaspettata: prova a
dimostrare il teorema di
Pitagora con… una bilancia,
delle forbici e del cartone.
Sul cartone disegna un triangolo rettangolo.
Su ciascuno dei suoi lati costruisci un quadrato
e ritaglialo.
Prendi la bilancia e distribuisci i tre quadrati in
modo che i suoi due piatti sino in equilibrio:
riesci?
?
Ti sarai certamente accorto che
l’equilibrio dei piatti della bilancia si
ottiene quando poniamo su un piatto
il quadrato costruito sull’ipotenusa e
sull’altro i due quadrati costruiti sui
cateti.
9. BIBLIOGRAFIA ED
ELENCO SITI
Gli Elementi di Euclide,
a cura di Attilio Frajese e Lamberto Maccioni,
Torino, UTET, 1970
C. B. Boyer,
Storia della matematica,
Cuneo, Arnoldo Mondadori, 1998
http://www-history.mcs.st-and.ac.uk/
La home page dell’archivio McTutor
http://aleph0.clarku.edu/~djoyce/java/elements/elements.html
Testo con commento degli Elementi, sul sito di David E. Joyce
della Clark University, USA
http://www.cut-the-knot.com/pytagoras/index.html
Sono illustrate varie dimostrazioni del teorema di Pitagora
http://sunsite.ubc.ca/DigitalMathArchive/Ratdolt/index.html
Ricco di fotografie dell'edizione degli Elementi curata da Erhard
Ratdolt nel 1894 (Londra)
http://sunsite.ubc.ca/DigitalMathArchive/Euclid/byrne.html
Ricco di fotografie dell'edizione degli Elementi curata da Byrne
nel 1847, in cui si fa uso dei colori.
http://www.cmontmorency.qc.ca/sdp/philo/pythagore.html
Varie informazioni su Pitagora
http://jeff560.tripod.com/theorem.jpg
Francobollo emesso dalla Grecia il 20 agosto 1955,
nell'occasione del Pythagoras's Congress. Riporta
un'immagine del teorema di Pitagora, in bianco e nero
http://jeff560.tripod.com/formula5.jpg
Francobollo emesso dal Nicaragua il 15 maggio 1971.
Riporta la formula ed alcune immagini connesse al teorema
di Pitagora