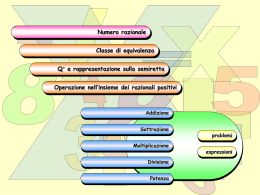
Una frazione si scrive
nel seguente modo:
n
d
NUMERATORE
DENOMINATORE
Il denominatore indica in quante parti congruenti
viene diviso un intero: non può essere uguale a zero.
Il numeratore indica quante parti dell’intero occorre
considerare.
1
8
Il biscotto è di due colori: la
frazione che rappresenta la
parte bianca è
 se il biscotto è diviso in 2 parti

se il biscotto è diviso in 4 parti

se il biscotto è diviso in 6 parti
Se mangi
2
:3
o 1/2 o
o 2/4 o
:3
2
o 3/6
del biscotto hai comunque mangiato la stessa
quantità di biscotto.
Due o più frazioni sono equivalenti se
rappresentano la stessa parte;
12
2 4
31
6 2
Principio di equivalenza
Moltiplicando o dividendo per uno stesso
numero sia il numeratore che il denominatore
si ottengono frazioni equivalenti.
ESEMPIO
Le due frazioni date sono equivalenti?
14
21
e
30
45
?
14
21
14 : 7 2

21 : 7 3
30
45
30 : 5 6

45 : 5 9
xSì
No
6:3 2

9:3 3
ESEMPIO
Le due frazioni date sono equivalenti?
24
40
e
30
42
?
24
40
24 : 2 12

40 : 2 20
30
42
30 : 6 5

42 : 6 7
Sì
No
x
12 : 4 3

20 : 4 5
ESEMPIO
Qual è la maggiore tra le seguenti frazioni?
7
5
o
?
11 8
7
5
11
8
• Si moltiplicano i due termini “in croce” 8 × 7 = 56
•Si confrontano i due prodotti ottenuti 11 × 5 = 55
Poiché 56 > 55 allora
7 5

11 8
Qual è la maggiore tra
2 2
e ?
7 5
2
5
Qual è la maggiore tra
8 4
e ?
9 5
8
9
Qual è la maggiore tra
9
7
e ?
11 6
7
6